python与机器学习1,机器学习的一些基础知识(完善ing)
目录
1 关于阈值θ和偏移量b和公式变形的由来
2 激活函数
3 关于回归,分类等
4 关于模型
5 关于回归
6 关于分类
7 关于误差和梯度下降
7-2 最小二乘法修改θ
8 深度学习
10 分类
11 参考书籍
1 关于阈值θ和偏移量b和公式变形的由来
比如很多信息传入可以表达为
WX=w1x1+w2x2+....这个是输入值,其中w表示权重,x表示信息
也有的写成 θX=θ1x1+θ2x2+....这个是输入值,都是一个意思
如果w1x1+w2x2+....>θ 就会激活
如果w1x1+w2x2+....<=θ 就不激活那么 w1x1+w2x2+....=θ就是判断公式
可以变形为
w1x1+w2x2+....=θ
w1x1+w2x2+....-θ=0
而尽量都取正数,就是
w1x1+w2x2+....+(-θ)=0
用系数b代替-θ
w1x1+w2x2+....+b=0
如果把b看成一个虚拟的输入信息,那么b的权重就是1
w1x1+w2x2+....+1*b=0
2 激活函数
一个最简单的函数,分段函数图形是直的,但是上下限也是[0,1]
- f(x)=0, if x<=0
- f(x)=1, if x>0
一个比较连续的, sigmod,分段函数图形是曲线,但是上下限也是[0,1]
sigmod,比较经典
- f(z)=1/(1-e^(-z))
3 关于回归,分类等
- 老的AI,逻辑
- 中间AI,
- 现在AI,数据
- 数据分为2部分
- 一部分训练数据
- 一部分,验证数据
- 有监督学习,回归分析,验证
- 半监督学习,
- 无监督学习,分类等
4 关于模型
回归,regression
用来处理,连续数据,如事件序列数据
比如按天记录的数据
分类,classification
数据带有标签
有监督学习
聚类,clustering
数据不带标签
无监督学习
5 关于回归
有1次回归函数,其中包含1元的,2元等等,如果是多元的需要求偏导数
一般来说,一次回归函数都是线性函数
有2次回归函数,其中包含1元的,2元等等,如果是多元的需要求偏导数
一般来说,二次回归函数都是曲线~
选择什么样的函数有差别
如果函数次数太低,拟合不够,可以用精确度变化曲线,精确度和回归度比较
如果函数次数太高,可能是过拟合,可能训练数据拟合好,但是验证数据拟合不好,
6 关于分类
分类是把 f(x) 做成了一个概率函数
可以看作是
f θ(x)>0.5 时 y=1
f θ(x)<=0.5 时 y=0
其实就是
θTX>0 时 y=1
θTX<=0 时 y=0
7 关于误差和梯度下降
误差函数,感觉很类似于方差函数
(y-f(x))^2
最梯度下降
采用最小二乘法? 可能会陷入局部最优
随机梯度下降
随机选择一些?一定能达到全局最优
随机梯度下降
最速下降,因为事先选取点的差别,可能陷入局部最优
而随机梯度下降,因为全局随机,理论上不会陷入局部最优,一定会找到全局最优
想象不规则的sinx这种函数曲线
1个随机数量
小批量随机梯度下降
7-2 最小二乘法修改θ
y=ax+b
y=θ0+θ1*x
根据一些原始数据,
大概200 → 500
但是随便假设θ0=1,θ1=2
fθ(x)=f(x)=y=1+2x
当时200 → 201
可见参数θ0=1,θ2=2 假设的不好
最小二乘法修改θ
E(θ)=1/2*∑(y-f(x))^2
E(θ)=1/2*∑(yi-f(x)i)^2
跟方差一样
还要去掉误差的正负影响,而是考虑误差与均值的差距的绝对值。
所以用平方
用平方,比abs更容易求导数
1/2也是为了求二次方的导数故意设计的,1/2或者2 只会改变函数形状的扁平还是高起,一般来说y=f(x) 值越大越高,值越小越扁平
所以最速下降法,就是求导数,也就是微分
导数函数求出来后,导数=0时的x 对应就是f(x)的极值
方法1 加上考虑函数的性质
比如 f(x)=x^2+2x+1这种往下凸出的,就是对应的最小值
方法2 比如 f(x)=x^2+2x+1 导数 f(x)'=2x+2
因此,最小值是x=-1对应
而且,
x>-1,f(x)'=2x+2>0 为正,f(x)递增
x<=-1,f(x)'=2x+2<0 为负,f(x)递减
所以
沿着与导数的符号相反的方向移动x,f(x) 就会朝着最小值前进
最速下降,梯度下降法
x=x-la*df(x)/dx
x=x-学习率*导数
学习率的选择要尽量小点,否则就会不容易收敛,或无法收敛
其实这就是更新的θ
如果f(x)=fθ(x1,x2,x3)=θ0+θ1*x+θ2*x^2 =θ*X
θ0=θ0-la*Σ(f(x)-y)
θ1=θ1-la*Σ(f(x)-y)x
θ2=θ2-la*Σ(f(x)-y)x^2
多变量,偏导数
如果f(x)=fθ(x1,x2,x3)=θ0*x0+θ1*x+θ2*x^2 =θ*X
变成2个向量点乘
8 和矩阵计算,矩阵内积点乘的关系
w1x1+w2x2+.....+wnxn
天生适合用矩阵计算
w1x1+w2x2+.....+wnxn=W*X
考虑到 偏移量(其实是和阈值有关系)
1*b+w1x1+w2x2+.....+wnxn=W*X
可变成
列向量 (1,w1,w2...wn) ,转行向量 (1,w1,w2...wn) T
列向量 (b,x1,x2...xn)
8 深度学习
输入层,中间层,输出层
中间层的宽度
中间层的层数,深度学习?
加宽度相对容易
加深度就会很难?
10 分类
假设W*X=w1x1+w2x2
如果W*X=w1x1+w2x2=0
假设w1 w2=1
x1+x2=0
W*X=|W||X|cosθ
其中cosθ 决定点乘内积符号 90-270,cos为负数,使得内积为负的向量
使得内积为正的向量
内积为正,两者相似
内积为负数,两者不相似
内积为0,两者垂直,完全不相关
11 参考书籍
《机器学习的数学》
《深度学习的数学》
《程序员的AI书》
相关文章:
)
python与机器学习1,机器学习的一些基础知识(完善ing)
目录 1 关于阈值θ和偏移量b和公式变形的由来 2 激活函数 3 关于回归,分类等 4 关于模型 5 关于回归 6 关于分类 7 关于误差和梯度下降 7-2 最小二乘法修改θ 8 深度学习 10 分类 11 参考书籍 1 关于阈值θ和偏移量b和公式变形的由来 比如很多信息传入可…...

移动应用开发介绍及iOS方向学习路线(HUT移动组版)
移动应用开发介绍及iOS方向学习路线(HUT移动组版) 前言 作为一个HUT移动组待了一坤年(两年半)多的老人,在这里为还在考虑进哪个组的萌新们以及将来进组的新朋友提供一份关于移动应用开发介绍以及学习路线的白话文…...
vue+uniapp校园寻物失物招领平台 微信小程序1f6z5
系统中的核心用户是管理员,管理员登录后,通过管理员菜单来管理后台系统。主要功能有:首页、个人中心、用户管理、物品分类管理、物品信息管理、物品归还管理、留言板管理、系统管理等功能。管理员用例如图3-7所示。 对于本网上失物招领小程序…...
物理内存分页机制--kmalloc及slub机制)
Linux内核--内存管理(三)物理内存分页机制--kmalloc及slub机制
一、引言 二、slub机制 ------>2.1、slub分配原理slub原理 ------>2.2、slub分配原理 ------>2.3、slub释放原理 ------>2.4、SLUB分配器 三、slub数据结构 ------>3.1、kmem_cache ------>3.2、kmem_cache_cpu ------>3.3、kmem_cache_node --…...
Shell - cron_protect.sh 监控 Python、Streaming 程序
目录 一.引言 二.Flink 程序监控 1.shell 脚本 2.crontab 配置 三.Python 程序监控 1.shell 脚本 2.crontab 配置 四.总结 一.引言 业务有流式处理数据的需求,需要 7x24 通过 Flink Python 程序进行处理。为了监控 Flink 与 Python 的程序运行状态并在程…...
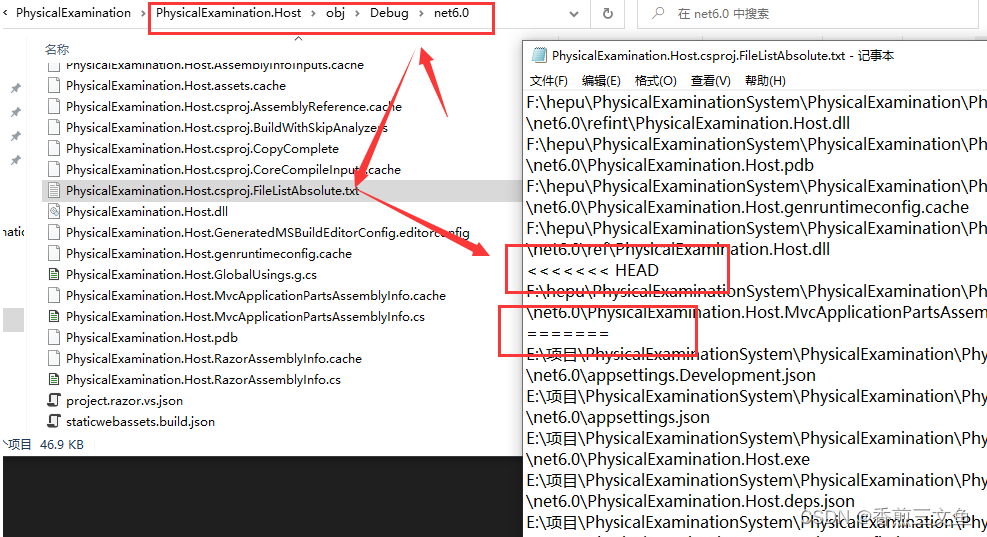
MSB3541 Files 的值“<<<<<<< HEAD”无效。路径中具有非法字符。
MSB3541 Files 的值“<<<<<<< HEAD”无效。路径中具有非法字符。 一般来说出现这个问题是因为使用git版本控制工具合并代码出现了问题,想要解决也很简单。 如图点击错误后定位到文件,发现也没有什么问题。 根据错误后边的提示&a…...

【赠书第9期】巧用ChatGPT高效搞定Excel数据分析
文章目录 前言 1 操作步骤 1.1 数据清理和整理 1.2 公式和函数的优化 1.3 图表和可视化 1.4 数据透视表的使用 1.5 条件格式化和筛选 1.6 数据分析技巧 1.7 自动化和宏的创建 2 推荐图书 3 粉丝福利 前言 ChatGPT 是一个强大的工具,可以为你提供在 Exce…...
会声会影2024旗舰版系统配置要求及格式支持
会声会影2024旗舰版是一款广受欢迎的视频编辑软件,它的最新版本,会声会影2023,已经发布。在这篇文章中,我们将探讨会声会影2024旗舰版系统配置要求及格式支持 会声会影2024是一款专业的视频剪辑软件,能够帮助用户制作高…...

【部署运维】docker:入门到进阶
0 前言 部署运维博客系列一共有三篇: 拥抱开源,将工作中的经验分享出来,尽量避免新手踩坑。 【部署运维】docker:入门到进阶 【部署运维】kubernetes:容器集群管理掌握这些就够了 【部署运维】pythonredisceleryd…...
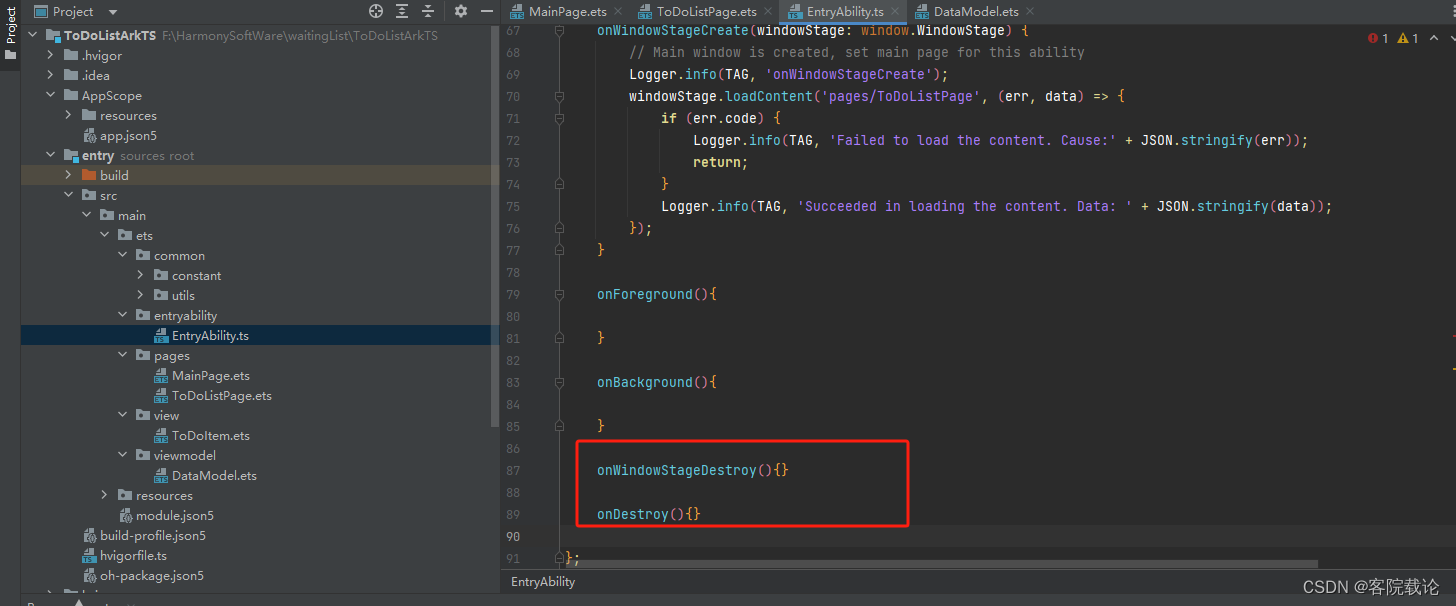
鸿蒙开发学习——应用程序框架
文章目录 UIAbility的生命周期Create状态WindowStageCreateForeground和Background前后台展示控制onWindowStageDestroyDestory 总结 UIAbility的生命周期 感觉这里他讲的不清晰,UIAbility的4个声明周期是Create、Foreground(桌面展示)、Back…...
)
Linux dd命令详解:如何从标准输入或文件中读取、转换并输出数据(附实例教程和注意事项)
Linux dd命令介绍 Linux dd命令用于读取、转换并输出数据。dd可以从标准输入或文件中读取数据,根据指定的格式来转换数据,再输出到文件、设备或标准输出。这个命令在备份硬盘、创建启动盘、数据恢复等场景中非常有用。 Linux dd命令适用的Linux版本 d…...
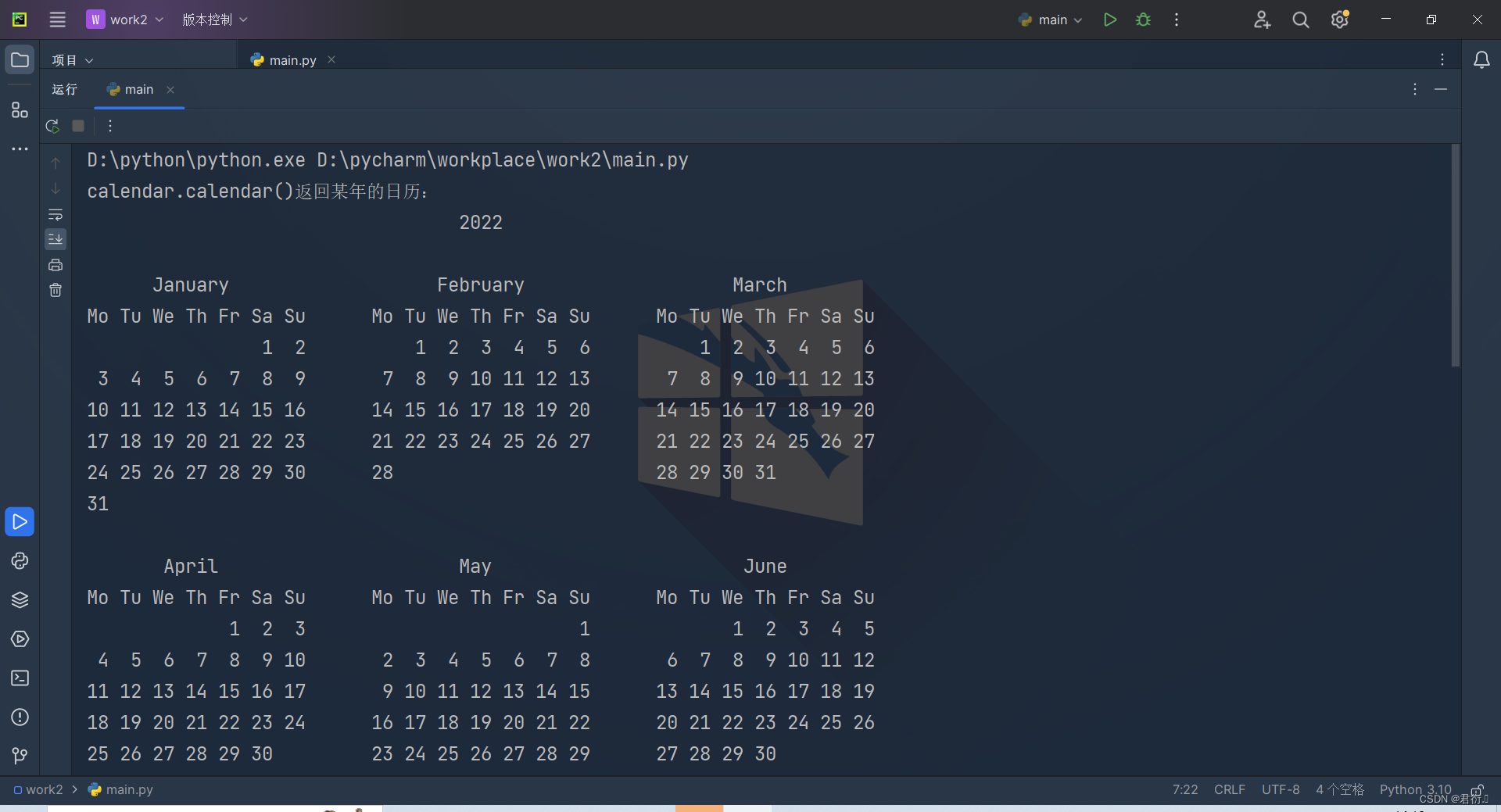
Python——常见内置模块
Python 模块(Modules)1、概念模块函数类变量2、分类3、模块导入的方法:五种4、使用import 导入模块5、使用from……import部分导入6、使用as关键字为导入模块或功能命名别名7、模块的搜索目录8、自定义模块 常见内置模块一、math模块二、rand…...

JAVA毕业设计112—基于Java+Springboot+Vue的宠物领养社区小程序(源码+数据库)
基于JavaSpringbootVue的宠物领养社区小程序(源码数据库)112 一、系统介绍 本系统前后端分离带小程序 小程序(用户端),后台管理系统(管理员) 小程序: 登录、注册、宠物领养、发布寻宠、发布领养、宠物社…...

golang log模块使用
在Go中,log 包是用于输出日志信息的标准库。以下是一些基本的 log 包的使用示例: 基本用法: package mainimport ("log" )func main() {log.Println("This is a log message.") } 运行程序,你会在控制台看到日…...

软件开发中的抓大放小vs极致细节思维
最近在开发过程中,遇到了好多次 “这个需求点这次要不要做?” 的问题, 主要有两方阵营,比如以研发主导的 “这次先不做、等必要的时候再做” ,另外一方是以PM主导的 “这个不做需求不完整,可能影响用户体验…...
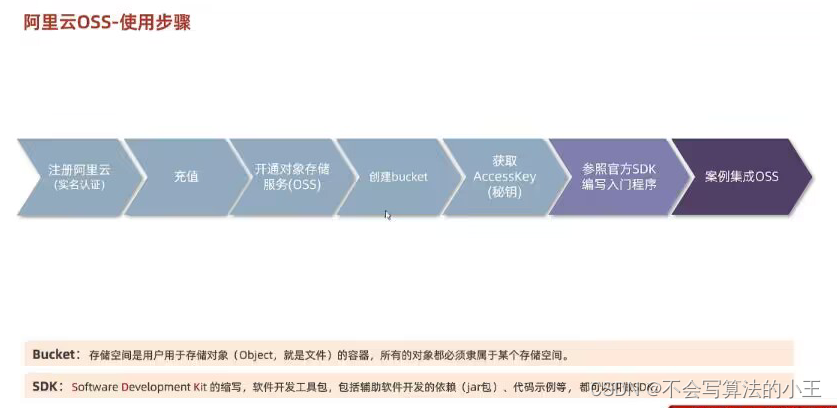
java文件上传以及使用阿里云OSS
JavaWeb 文件上传本地存储阿里云OSS配置文件 yml配置文件 文件上传 前端页面三要素: 表单项type“file” 表单提交方式post 表单的enctype属性multipart/form-data 本地存储 保证上传的文件不重复 //获取原始文件名String originalFilename image.getOriginalFi…...
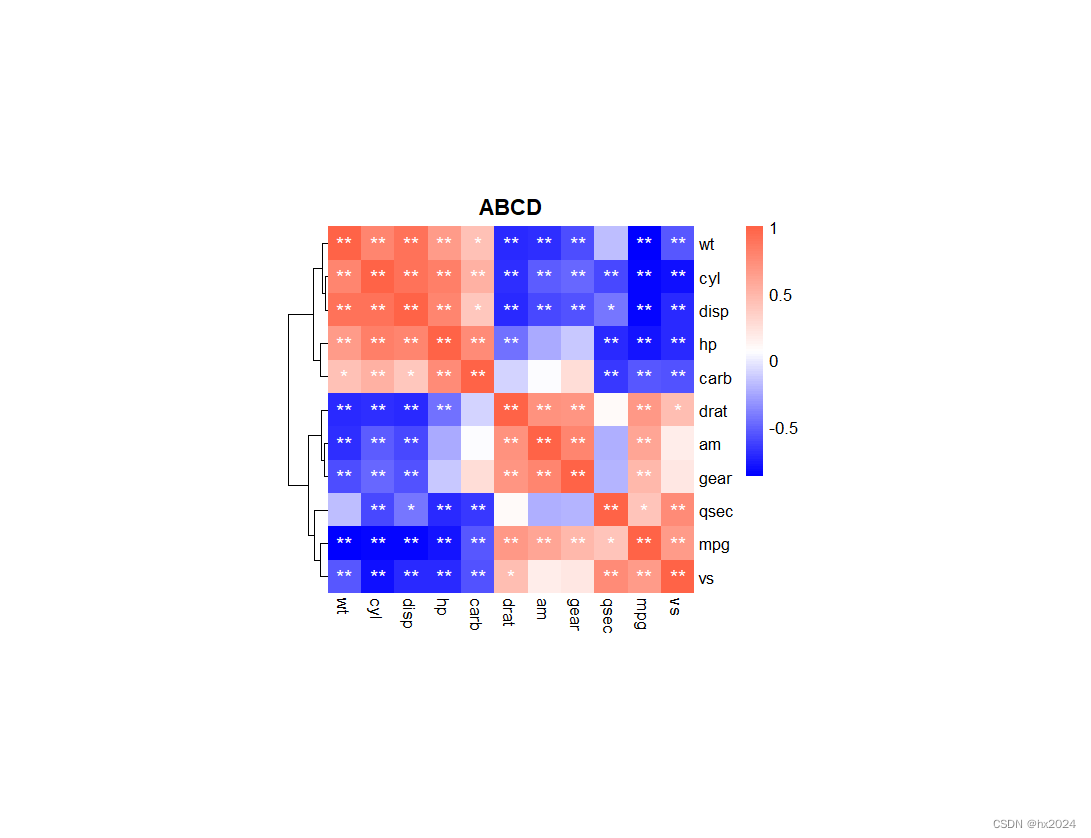
相关性分析和作图
相关的类型 1. Pearson、Spearman和Kendall相关 Pearson 积差相关系数衡量了两个定量变量之间的线性相关程度。(连续) Spearman等级相关系数则衡量分级定序变量之间的相关程度。(分类) Kendall’s Tau 相关系数也是一种非参数的…...
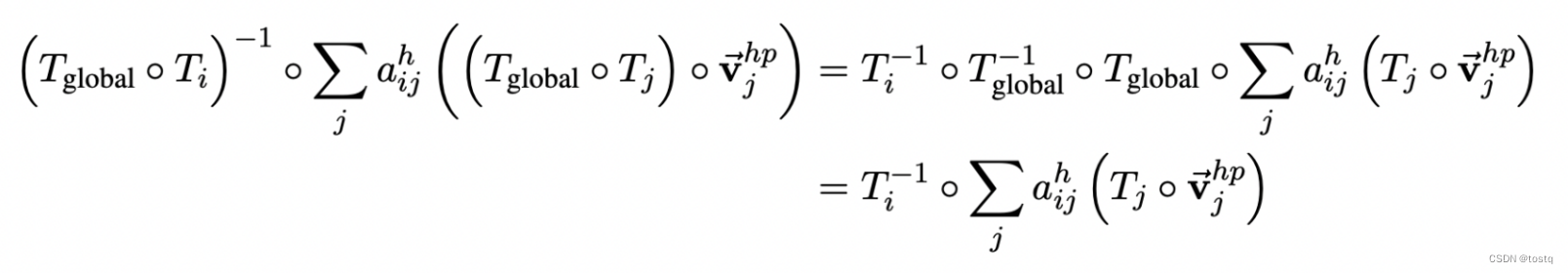
AlphaFold的原理及解读
1、背景 蛋白质是生物体内一类重要的生物大分子,其结构复杂多样,蛋白质的结构对于理解其功能和参与的生物学过程具有重要意义。从生物学角度上看,蛋白质的结构可以分为四个层次:初级结构、二级结构、三级结构和四级结构。 初级结…...
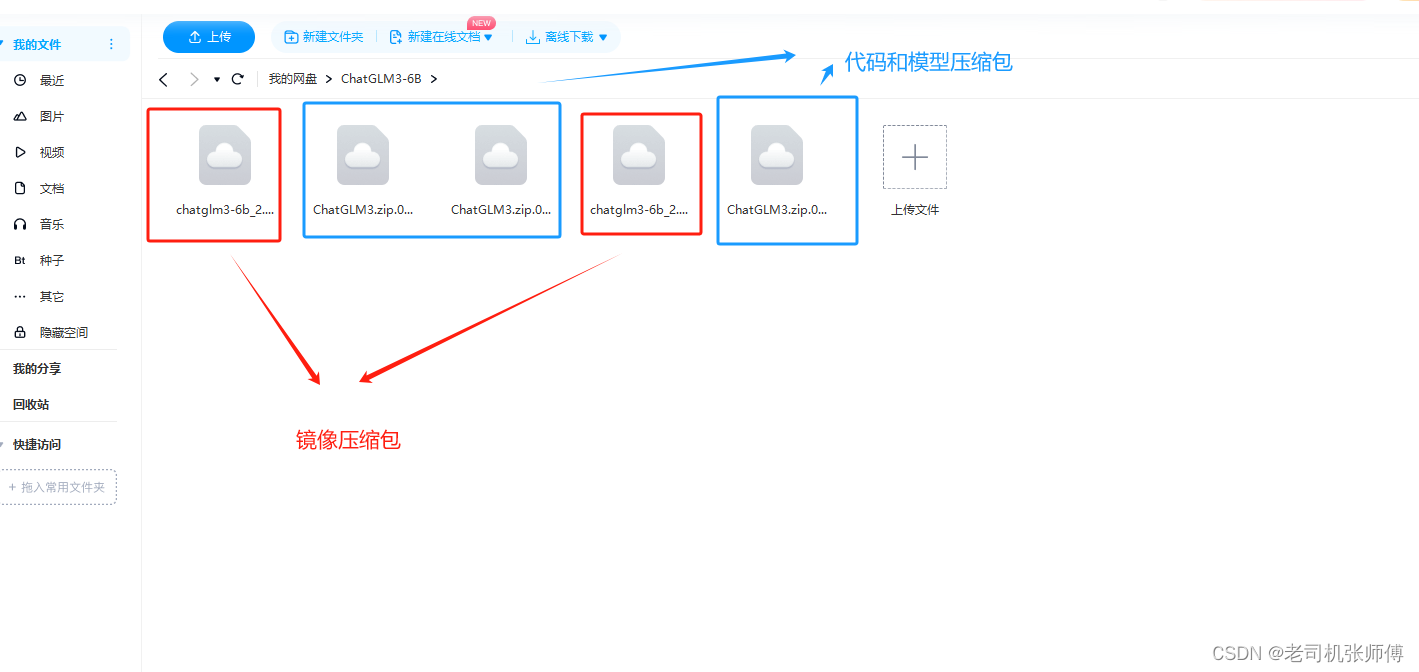
【ChatGLM3-6B】Docker下快速部署
【ChatGLM2-6B】小白入门及Docker下部署 前提下载安装包网盘地址 开始安装加载镜像启动镜像进入容器启动模型交互页面访问页面地址 前提 安装好了docker安装好了NVIDIA显卡16G 下载安装包 网盘地址 这里因为网盘上传文件有大小限制,所以使用了分卷压缩的方式…...
两部手机数据传输后备忘录不见了怎么回事
想必很多人都遇到过,当两部手机进行备忘录数据传输后,突然发现备忘录不见了,这让人不禁着急上火,我也曾经遇到过这种事情导致很多重要的内容都丢失了。 一般出现这种情况可能是因为,两部手机使用的是不同的云服务&…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
