树与二叉树堆:链式二叉树的实现
目录
链式二叉树的实现:
前提须知:
前序:
中序:
后序:
链式二叉树的构建:
定义结构体:
初始化:
构建左右子树的指针指向:
前序遍历的实现:
中序遍历的实现:
后序遍历的实现:
求二叉树结点个数:
写法1:
写法2:
求树的叶子结点个数:
求树的高度:
求第K层结点:

链式二叉树的实现:
前提须知:
链式二叉树的实现主要服务于那些不能被数组存储的非满二叉树和非完全二叉树,而在这些二叉树中,我们又将它们的组成结构进行拆分,分别是根、左子树、右子树。
而左子树和右子树又可以根据该结构划分为它们的根、左子树、右子树。

前序:
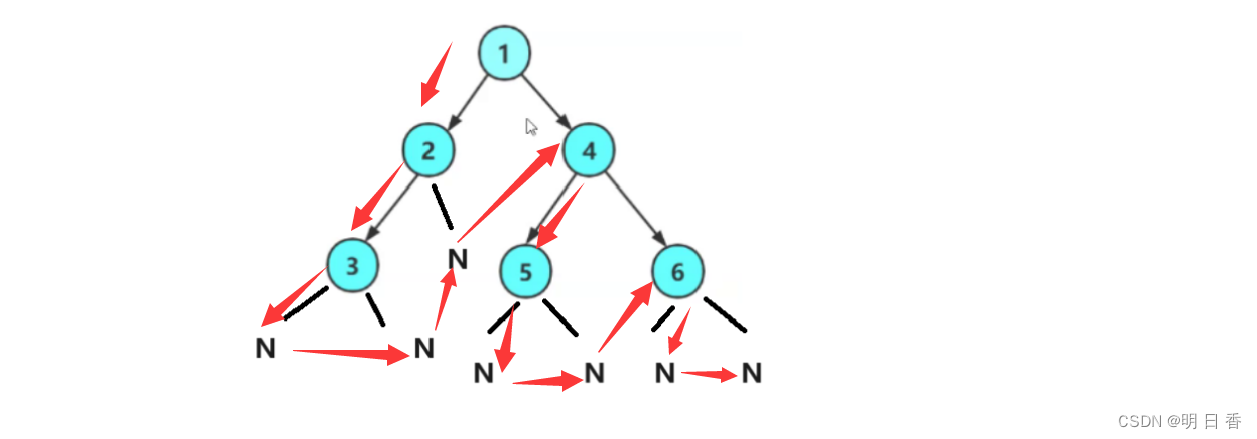
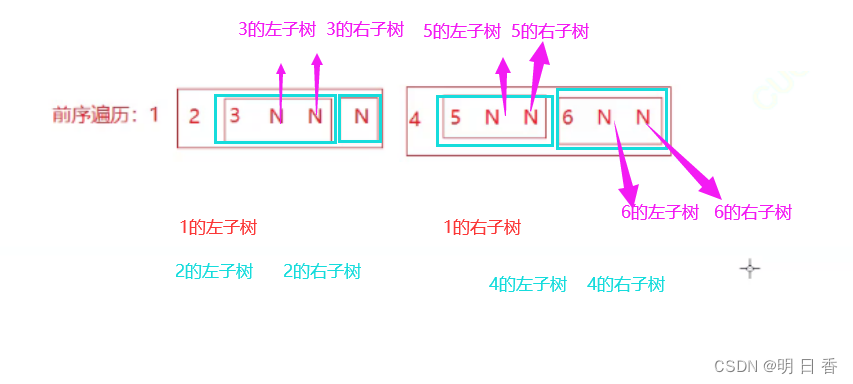
是将二叉树以根、左子树、右子树顺序进行结构划分遍历的遍历方式。
如图所示:其中N表示结点是NULL
以数字表示为:1 2 3 N N N 4 5 N N 6 N N
中序:
是将二叉树以左子树、根、右子树顺序进行结构划分遍历的遍历方式。
如图所示:其中N表示结点是NULL
以数字表示为N 3 N 2 N 1 N 5 N 4 N 6 N
后序:
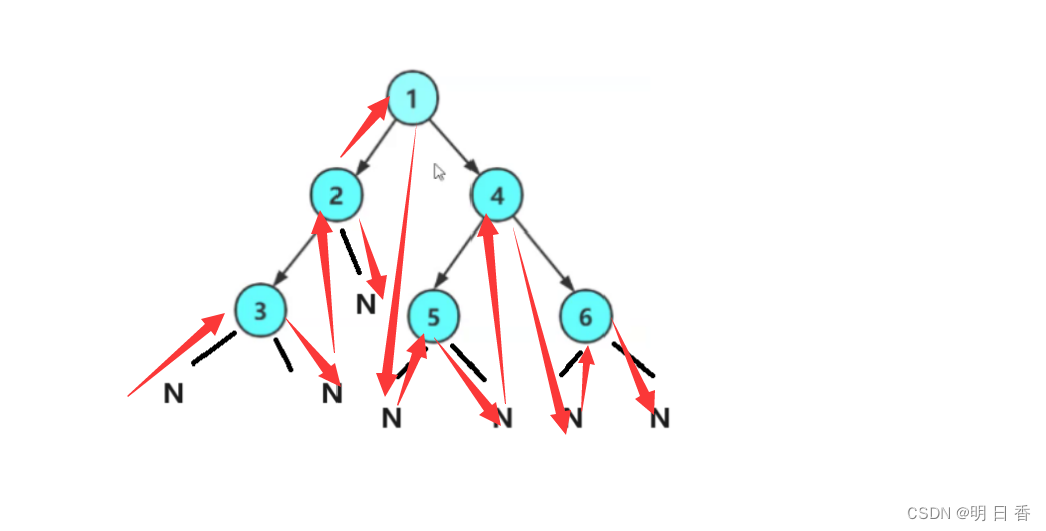
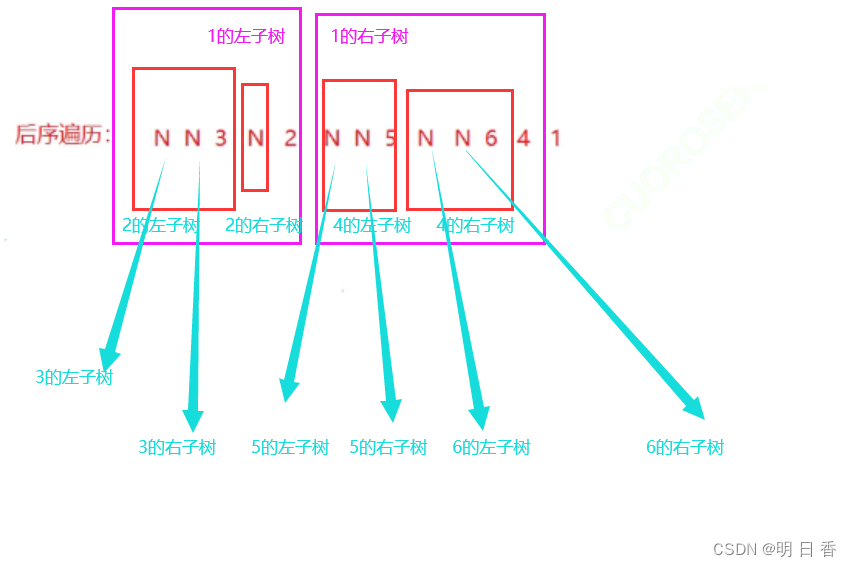
是将二叉树以左子树、右子树、根顺序进行结构划分遍历的遍历方式。
如图所示:其中N表示结点是NULL
以数字表示为N N 3 N 2 N N 5 N N 6 4 1
链式二叉树的构建:
万恶之源~递归!

定义结构体:
一个链式二叉树,需要有存放结点元素的data、需要有两个分别指向左子树、右子树的指针。
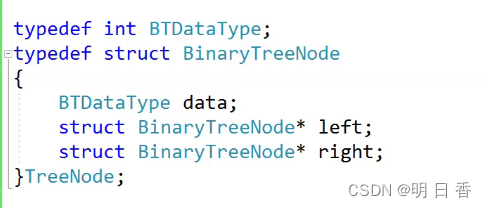
初始化:
开辟空间构建结点:
记得将构建的结点的左右子树指针进行初始化,以及结点元素进行赋值。

构建左右子树的指针指向:
构建的结点如上图的二叉树结构所示。

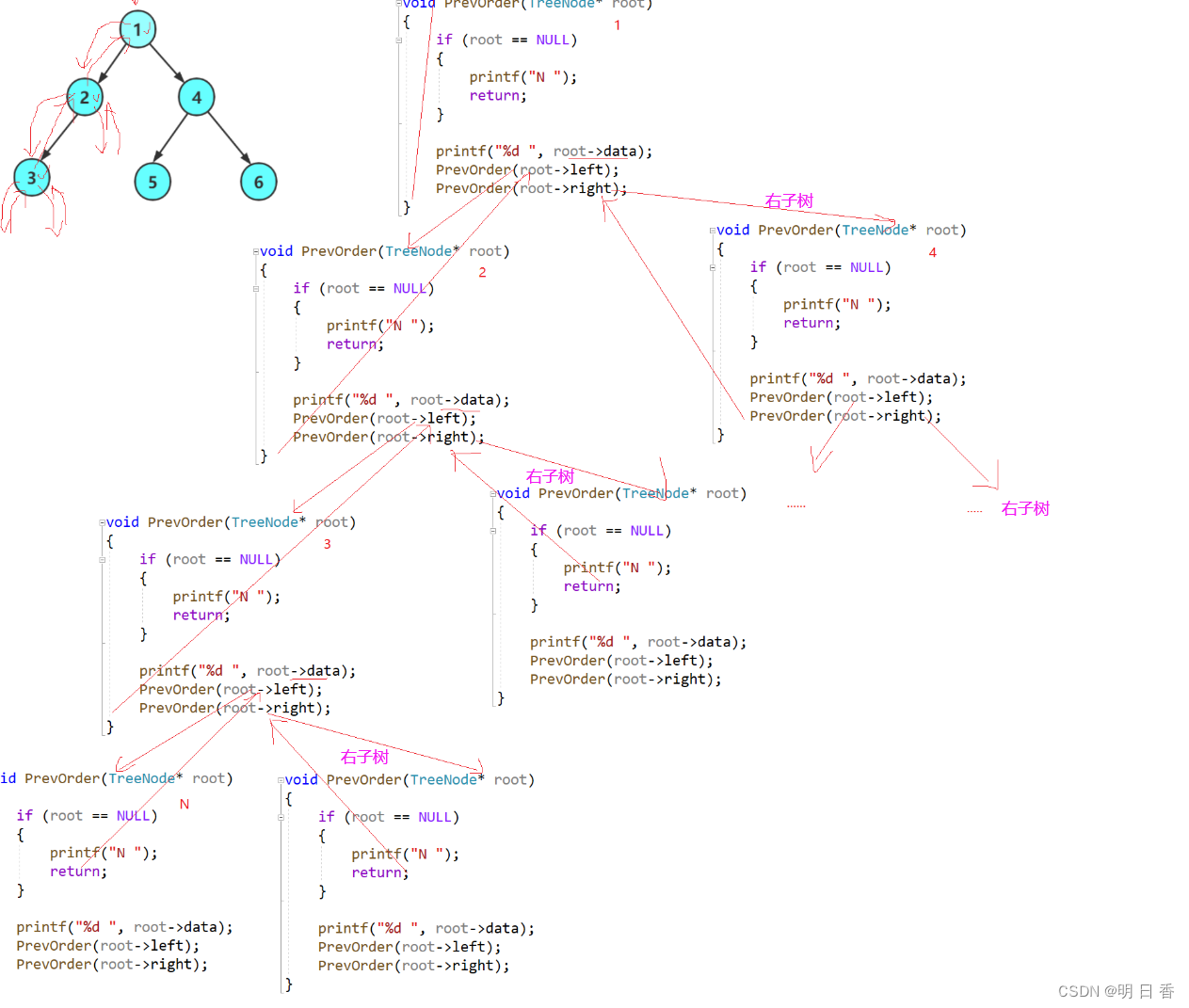
前序遍历的实现:

前序遍历的思路是,根、左子树、右子树,所以先要打印根,在前往根的左子树,而根的左子树又可以进行前序的遍历,因此使用递归的思想,先不断地进行调用以此抵达最左边的结点,随后逐级的递归,然后再迈向右子树进行相同的操作,也就是调用进入左子树,然后逐级递归……
二叉树走向图

代码调用思路图
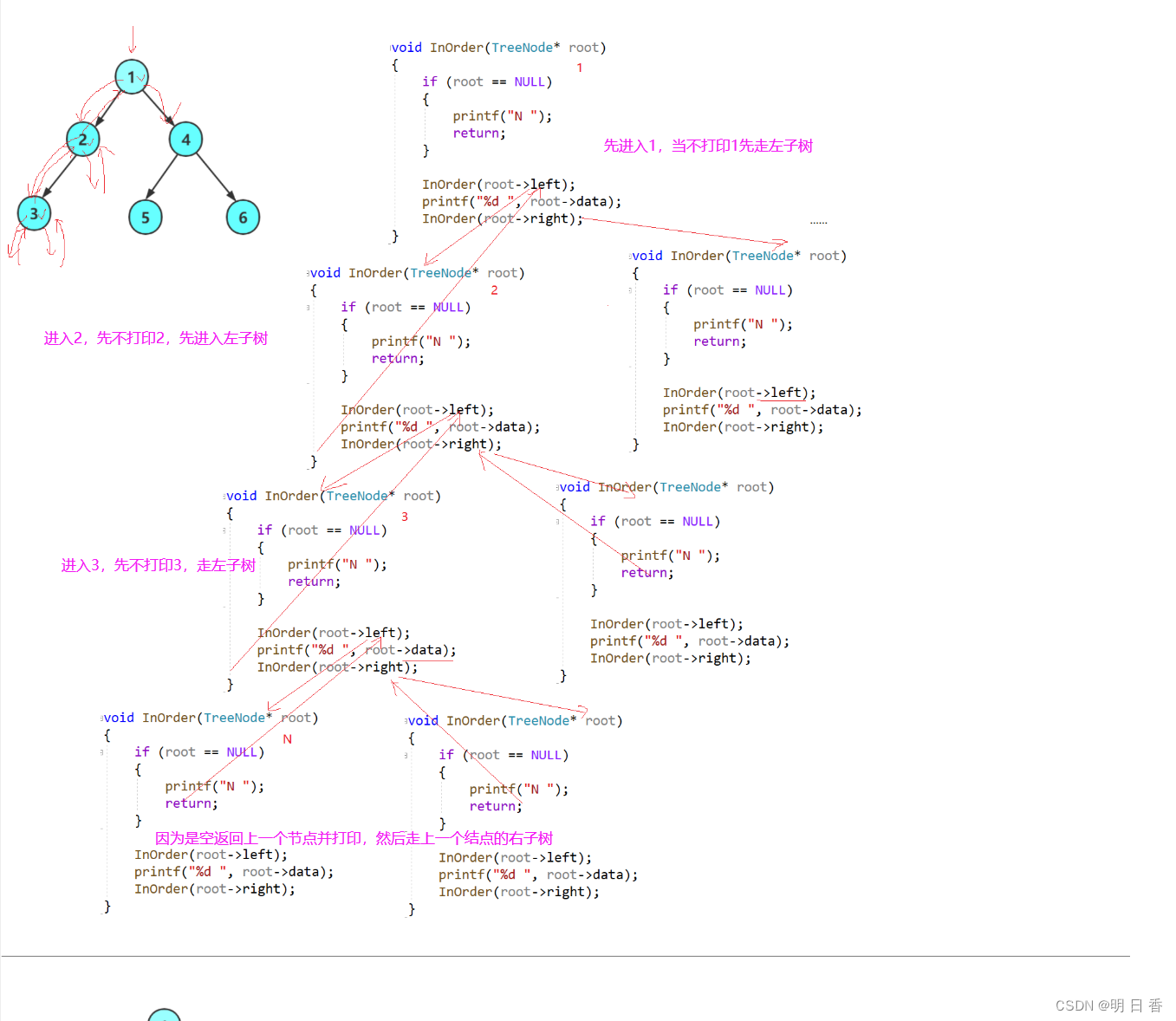
中序遍历的实现:

中序的遍历思想是左子树、根、右子树,所以再打印上是先打印左子树而后再打印根结点,最后再打印右子树,所以利用递归的思想,想要遍历到最左的结点,之后打印,随后进入右子树中,接着遍历左子树,以此类推……
二叉树走向图

代码思路调用图
后序遍历的实现:
后序就是中序的指向右子树和打印结点子树互换顺序即可
求二叉树结点个数:
用递归的思想,将问题化解为左子树的结点个数+右子树的结点个数+根结点的结点个数。
- 而左右子树的结点个数又可以划分为左子树的结点个数+右子树的结点个数+根结点的结点个数。
- 因此,本题就可以变为如果当前结点不是NULL那++size,如果是NULL则返回return。
- 而再递归中return 也仅仅只是跳出了这一回的进程,返回上一次调用的进程并进入下一条代码中。
写法1:
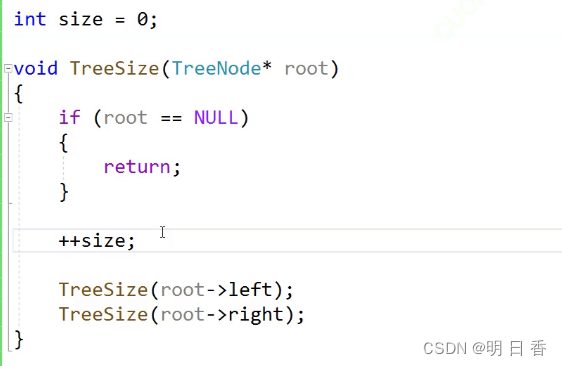
图解

写法2:
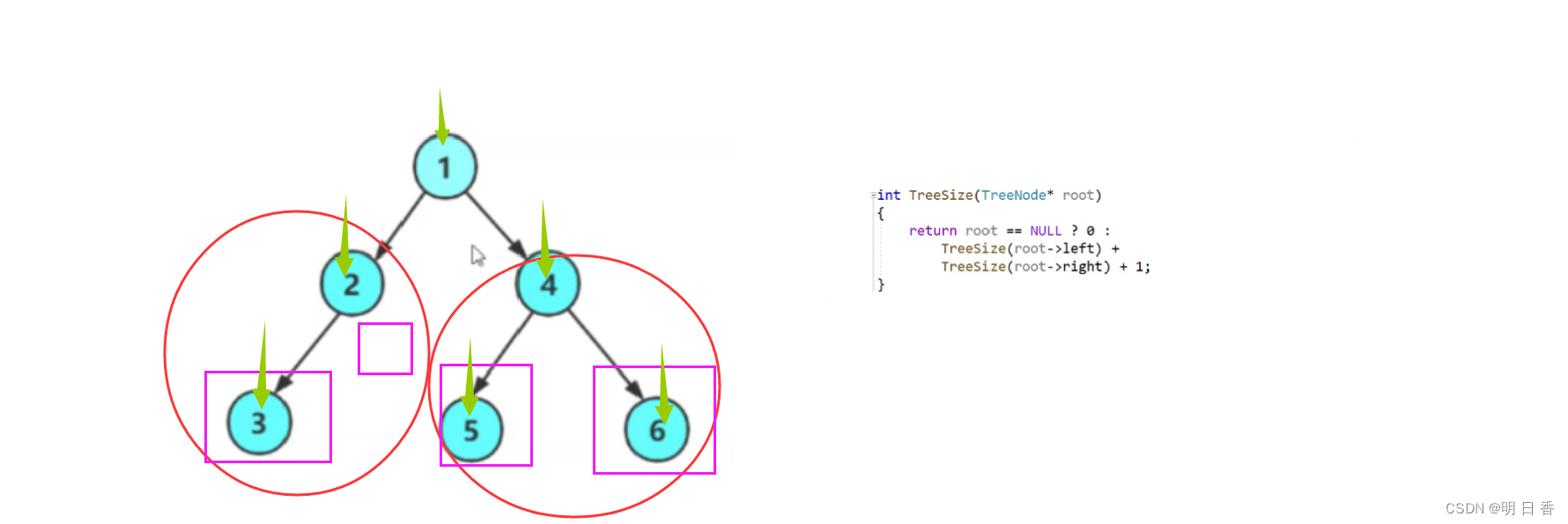
写法2就是彻底的简化了写法1,使用了三目运算符,将++size问题彻底变为了1的累加。
如果root = NULL 则返回0,如果不等于NULL 则进行调用 进入左子树的递归调用和右子树的递归调用

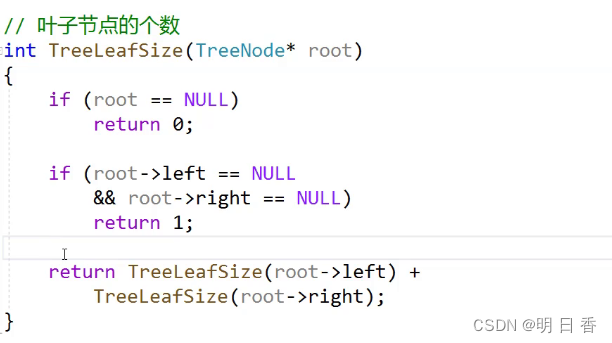
求树的叶子结点个数:
叶子结点概念:树与二叉树堆:树-CSDN博客
该问题的核心可以拆分为 树的叶子结点个数 = 左子树叶子结点个数+右子树叶子结点个数
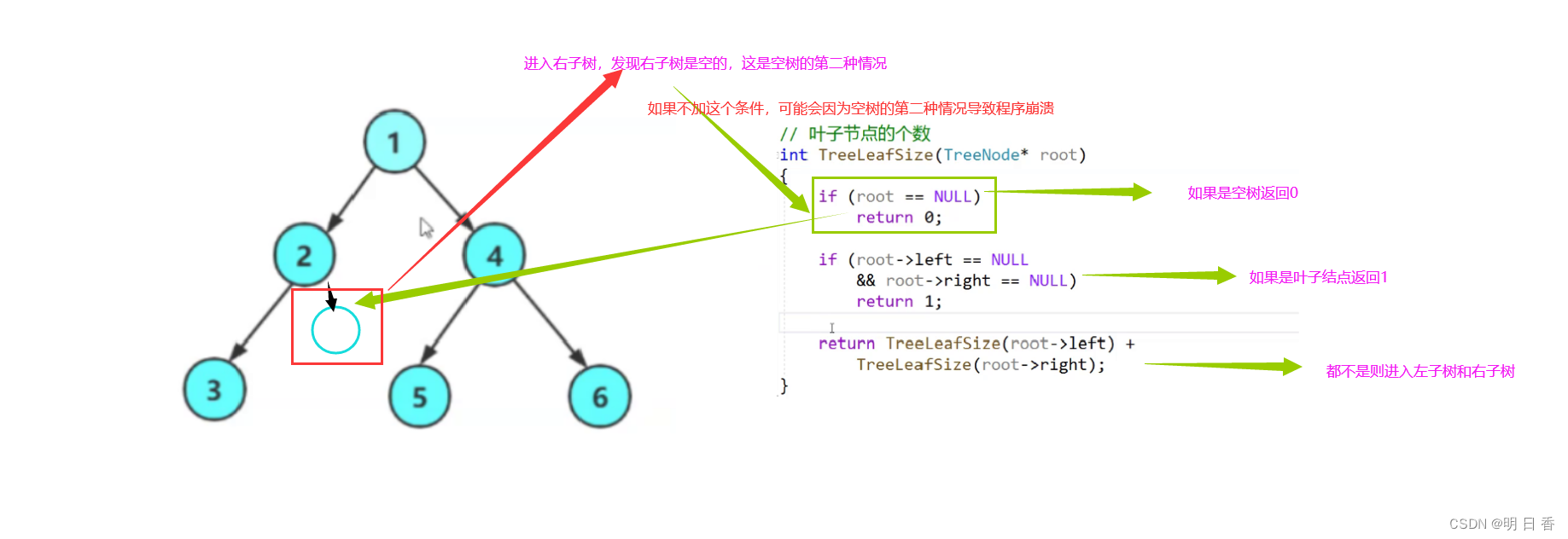
本问题其实是上一个问题的进阶版本,本质上多了两个条件,也就是当结点的左右子树指针指向的是NULL时便返回1,表示该节点是叶子节点,而非叶子节点则进入调用,分别进入结点的左右子树进行递归调用,知道root == NULL 或者是叶子节点,进行return 返回上一个结点开始逐级返回……
求树的高度:
本问题可以转化为求树的高度是左子树、右子树二者中高度最大的+1 ,这个1是根结点,由此可以化为1的累加问题。
也便是通过 root == NULL 进行逐级的返回,和+1来达成1的累加。

- 如上代码所示,进入了最左边的结点后,以root == NULL 为返回条件
- 当最左边结点的左子树的leftheight因为root == NULL 返回0, 结束后返回到了上一个结点(最左结点),并进入了该结点(最左结点)的右子树
- 随后右子树又以root == NULL 返回后,进入两个子树的高度对比
- 因为NULL 所以这里的两个返回值是 0 +1 和 0 + 1 进行对比,所以最后返回1 到本结点(最左结点)的上一个节点 (最左结点的父亲结点)

使用特殊函数进行比较

求第K层结点:
假设,如果再根节点是求第K层,那么再根结点的左右子树的根结点来看是k-1层
- 又因为 条件 root ==NULL 表示树是空的,所以返回0,而k == 1表示树只有一个根结点,所以只有一个结点
- 又因为树可以拆分左右子树和根,而左右子树又可以继续拆分,而又是求第K层的结点个数,所以可以通过K==1这个条件进行返回进行回代数值。
- 也因此可以使用k>1和k-1进行不断地调用到第K层,然后进行回代返回值
注意,是带回返回值,而不是将返回值进行累加
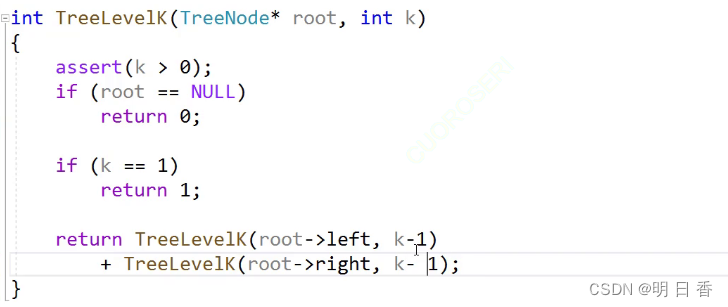
思路图



相关文章:

树与二叉树堆:链式二叉树的实现
目录 链式二叉树的实现: 前提须知: 前序: 中序: 后序: 链式二叉树的构建: 定义结构体: 初始化: 构建左右子树的指针指向: 前序遍历的实现: 中序…...

C++面试的一些总结day1:指针和引用的区别
文章目录 指针和引用的区别和作用定义区别作用 指针和引用的区别和作用 定义 指针:指针是一个变量,其值为指向对象的内存地址,而不是值本身。引用:可以理解为对象的别名,是另外一个变量的直接别名,用于创…...
Java核心知识点整理大全15-笔记
Java核心知识点整理大全-笔记_希斯奎的博客-CSDN博客 Java核心知识点整理大全2-笔记_希斯奎的博客-CSDN博客 Java核心知识点整理大全3-笔记_希斯奎的博客-CSDN博客 Java核心知识点整理大全4-笔记-CSDN博客 Java核心知识点整理大全5-笔记-CSDN博客 Java核心知识点整理大全6…...

初始本地仓库推送到远程仓库-git
背景(问题描述) 下面的git的操作符合的情况是: ①本地初始化一个仓库,但是还没有和远程仓库相关联; ②远程仓库也刚刚创建,里面啥也没有 然后目前就想将本地的仓库的内容和远程仓库相关联并推送到远程仓…...

OpenCV | 图像梯度sobel算子、scharr算子、lapkacian算子
import cv2 #opencv读取的格式是BGR import numpy as np import matplotlib.pyplot as plt#Matplotlib是RGB %matplotlib inline 1、sobel算子 img cv2.imread(pie.png,cv2.IMREAD_GRAYSCALE) cv2.imshow(img,img) cv2.waitKey() cv2.destroyAllWindows() pie图片 dst cv2.S…...
WS2812灯条基于WLED开源项目无门槛使用简介
WS2812灯条基于WLED开源项目无门槛使用简介 📌项目github地址:https://github.com/Aircoookie/WLED📍WLED详情地址:https://kno.wled.ge/🎈网页在线烧录固件地址:https://install.wled.me/ ✨ 仅作为使用的…...
基于AOP的声明式事物控制
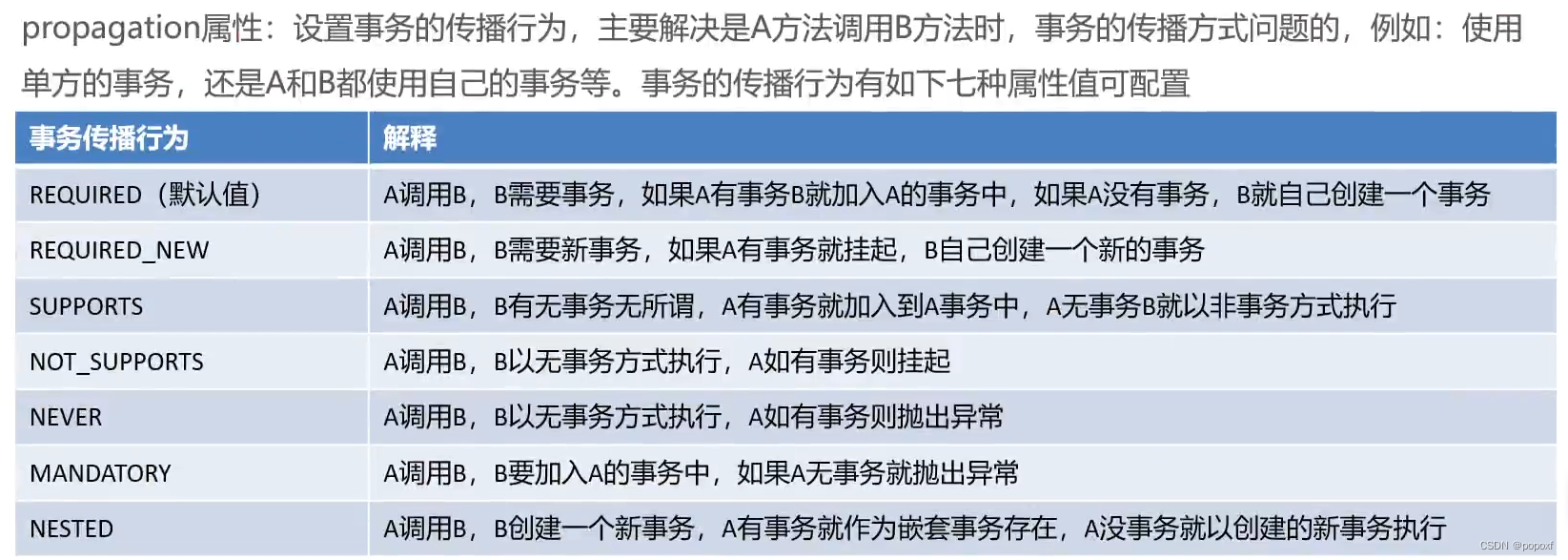
目录 Spring事务编程概述 基于xml声明式事务控制 事务属性 isolation timeout read-only propagation 全注解开发 Spring事务编程概述 事务是开发中必不可少的东西,使用JDBC开发时,我们使用connection对事务进行控制,使用MyBatis时&a…...
第七节HarmonyOS UIAbility生命周期以及启动模式
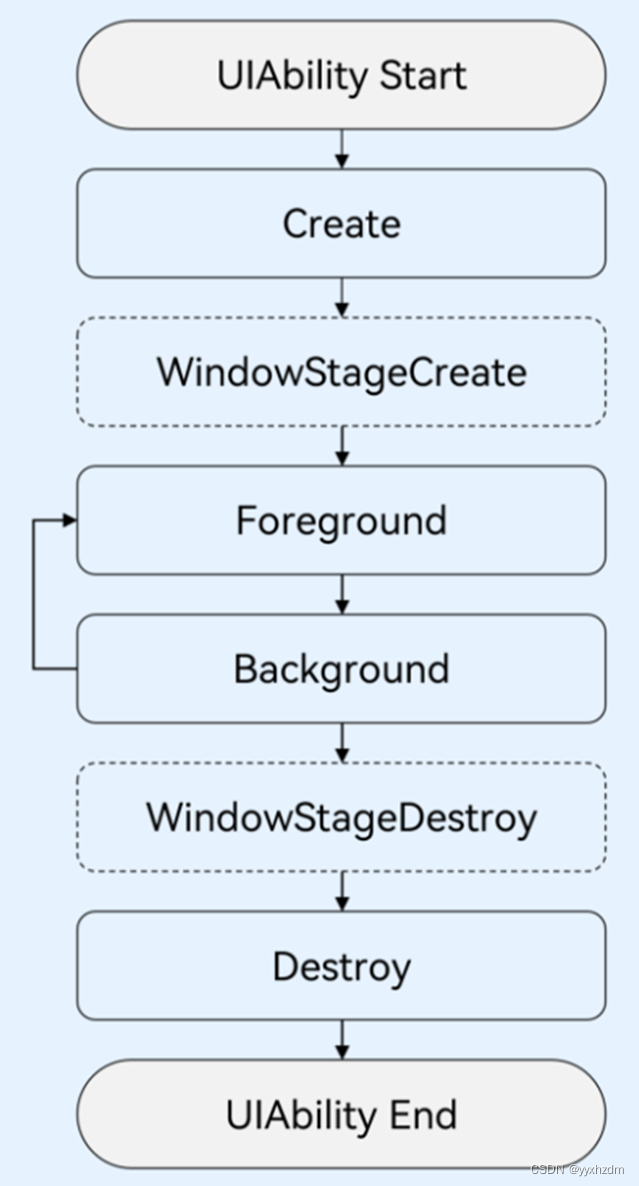
一、UIAbility生命周期 为了实现多设备形态上的裁剪和多窗口的可扩展性,系统对组件管理和窗口管理进行了解耦。UIAbility的生命周期包括Create、Foreground、Background、Destroy四个状态,WindowStageCreate和WindowStageDestroy为窗口管理器(…...
matlab设置背景颜色
matlab默认的背景颜色是纯白RGB(255,255,255),纯白太刺眼,看久了,眼睛会酸胀、疼痛,将其改成豆沙绿RGB(205,123,90),或者给出浅绿色RGB(128,255,255), 颜色就会柔和很多,眼睛感觉更舒适。 下面介绍在…...
)
Linux gzip命令用法详解:如何压缩和解压文件(附实例教程和注意事项)
Linux gzip命令介绍 Linux gzip命令用于压缩文件。它可以减小文件的大小以节省磁盘空间,并且可以通过gzip命令将多个文件合并成一个压缩文件。 Linux gzip命令适用的Linux版本 Linux gzip命令可以在多数Linux发行版(如Debian、Ubuntu、Alpine、Arch L…...

初刷leetcode题目(11)——数据结构与算法
😶🌫️😶🌫️😶🌫️😶🌫️Take your time ! 😶🌫️😶🌫️😶🌫️😶🌫️…...

基于SSM框架的图书馆管理系统设计与实现
基于SSM框架的图书馆管理系统 摘要:在21信息时代中,编程技术的日益成熟,计算机已经是普通使用的。编程技术的实现是基于计算机硬件上,计算机科学与技术的进步,让时代发展的更快,更加信息化。人们都是学习如…...

【面试】css预处理器之sass(scss)
目录 为什么引入css预处理器 可读性 嵌套:关系明朗 选择器 属性 伪类‘’ 变量:语义明确 默认变量:美元符号 $ 变量名:值 !default 全局变量::global { $global-x: } 变量插值:#{} map键值对:$…...

Android设计模式--享元模式
水不激不跃,人不激不奋 一,定义 使用共享对象可有效地支持大量的细粒度的对象 享元模式是对象池的一种实现,用来尽可能减少内存使用量,它适合用于可能存在大量重复对象的场景,来缓存可共享的对象,达到对象…...

人工智能对我们的生活影响有多大
人工智能给我们的生活带来了巨大的影响!它像魔术师一样,帮我们解决问题、提供建议,甚至预测未来。从智能手机到智能家居,人工智能让我们的生活变得更便捷、更智能。它是我们生活中的得力助手,让我们感受到科技的魅力&a…...

【蓝桥杯选拔赛真题26】C++字符串逆序 第十三届蓝桥杯青少年创意编程大赛C++编程选拔赛真题解析
目录 C/C++字符串逆序 一、题目要求 1、编程实现 2、输入输出 二、算法分析...

antd vue a-select 下拉框位置偏移
问题 下拉框未固定 原因 select下拉框的定位是根据body定位 解决方法 在select 标签中添加: :getPopupContainer"(triggerNode) > (triggerNode.parentElement)" :getPopupContainer"(triggerNode) > (triggerNode.parentElement)"…...
Windows10免安装PostgreSQL
1. PostgreSQL简介2. 下载3. 安装环境4. 安装 4.1. 初始化数据库4.2. 启动数据库4.3. 注册服务4.3. 卸载服务 1. PostgreSQL简介 PostgreSQL 是一种特性非常齐全的自由软件的对象-关系型数据库管理系统,是以加州大学计算机系开发的 POSTGRES 4.2版本为基础的对象关…...

lua_next
lua_pushnil(L);while(lua_next(L, -2)){// 栈状态:key : -2 value : -1// do something lua_pop(L, 1);} lua_next 先弹出一个值, 再放一对pair 到栈上, 参数 index 是表的位置 调用后: -1:value -2:key 因为会先…...

svn服务端安装
1.下载svn 2.创建一个文件夹 /usr/svn/dev 3.svnadmin create /usr/svn/dev 4.修改/usr/svn/dev/config下的目录的配置文件 authz:权限配置文件,控制读写权限passwd:账号密码配置文件svnserve.conf:svn服务器配置文件 修改svnse…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...