信号类型(通信)——最小频移键控(MSK)
系列文章目录
《信号类型(通信)——仿真》
《信号类型(通信)——QAM调制信号》
《信号类型(通信)——QPSK、OQPSK、IJF_OQPSK调制信号》
目录
前言
一、MSK信号特点
1.1、最小频移
1.2、相位连续
二、MSK调制与解调
2.1、调制原理
2.2、解调原理
三、MSK信号频谱
四、仿真
总结
前言
本文为MSK调制信号的学习笔记,介绍了MSK调制起源,即MSK是一种特殊的FSK调制。并根据MSK信号特征由FSK信号模型推导了MSK的信号模型;并基于MSK信号模型介绍了MSK信号调制与解调原理;最后结合仿真加深对MSK信号调制与解调的理解。此外补充了MSK信号的频谱表达式,公式的具体推导没有研究,文后有参考文献,感兴趣的可以自行推导,也欢迎在评论区给出相应的推导过程。(文末有彩蛋)
一、MSK信号特点
最小频移键控(MSK)调制方式是频移键控(FSK)调制方式的特例。相比于FSK调制,MSK调制满足两个条件:正交条件下最小频率间隔(最大频移为比特速率的1/4);信号相位连续。满足上述条件的MSK信号能量99.5%被限制在数据传输速率的1.5倍的带宽内。此外MSK属于恒包络数字调制技术,系统可以使用廉价高效的非线性器件。下面基于最小频移以及相位连续两个条件简单推导MSK信号模型。
1.1、最小频移
针对01码元对应波形的正交条件,假设FSK码元波形为:
考虑FSK调制码波形的正交性,有:
分别根据积化和差公式、定积分公式以及的假设条件,可以得到:
(3)
为了使上式在任意的下都成立,则需要满足:
此时只能采用非相干检波法接收。针对相干接收,初始相位确定,当,则仅需要满足:
1.2、相位连续
在最小频差为下,可令MSK信号模型为:
为了保证码元波形的正交性,此时载频需要满足:
考虑相位是连续,MSK信号中
相位是存在跳变,需要通过调整
使得MSK信号相位连续,即需要满足:
由此可得:
为了满足,则
,因此需要将原始01码通过双极性转换,得到+1,-1码。将MSK信号进行IQ正交分解得:
(10)
其中
二、MSK调制与解调
2.1、调制原理
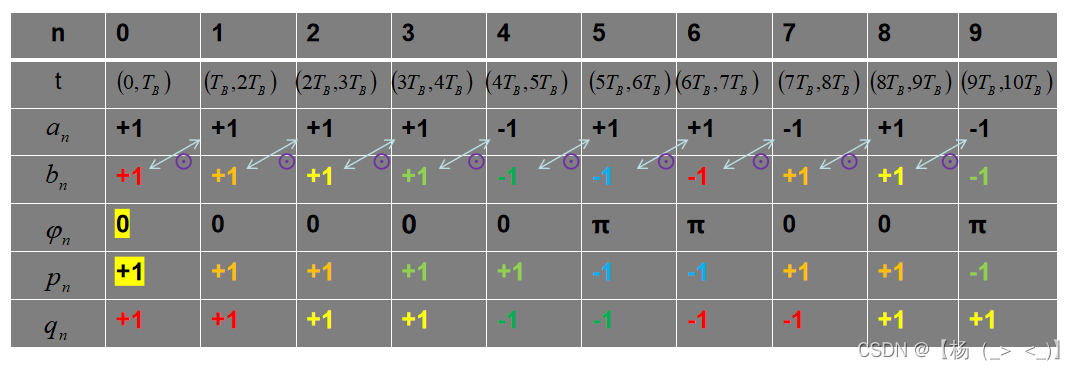
MSK信号可以按照公式(10)生成,我们可以根据公式(9)计算,再由公式(11)计算得到
,但是这种信号生成方式在实际电路实现时并不方便,为此引入上图表所示的
的生成方案,首先基于差分编码生成码序列:
其中表示同或,
。
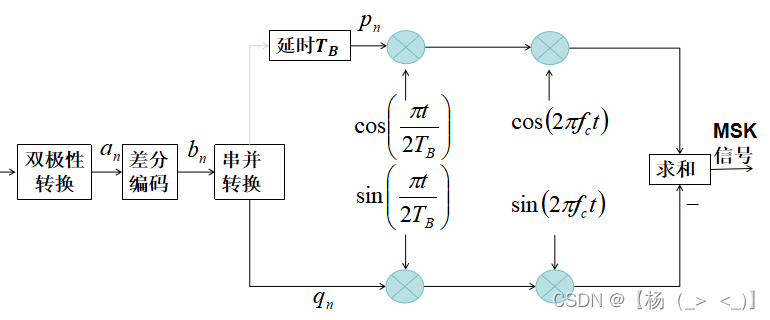 上图表示MSK信号生成的流程图,首先01比特流经过双极性转换变成双极性码
上图表示MSK信号生成的流程图,首先01比特流经过双极性转换变成双极性码,在经过差分编码以及串并转换得到
,再分别经过半个波特的频率调制以及载频调制混合得到最终发射的MSK信号。
2.2、解调原理
对公式(10)所示MSK信号进行载波提取得到:
则在I路采样判决点上对应的I值为:
则在Q路采样判决点上对应的Q值为:
由公式(14)(15)可得:
我们可以对上述采样值大于0的判为+1,小于0判为-1,然后基于公式(16)还原出,为了提高信噪比,我们可以在采样点附近左右对称的区域
内求积分得到信噪比更好的判决统计量。最终解调原理图下:
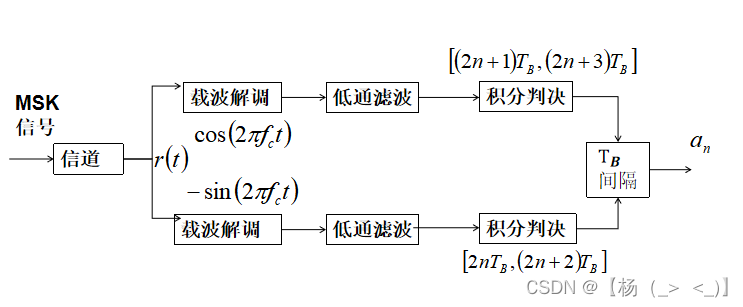
此外由公式(13)构成的复信号可以得到相位历程:
由此相位历程也可以解调出。
三、MSK信号频谱
对公式(10)进行积化和差得:
其中,根据
错位延时的特点,
的变化周期为
。考虑随机生成的码序列,MSK信号功率谱密度为:
其中表示被调制波形功率,从公式(18)可以看出MSK信号功率谱密度随偏移载频量的四次方成反比衰减,带外能量泄露很少。
四、仿真
参数设置,符号速率60kHz,采样率12 Mz,载频 1.5MHz,码序列随机生成。
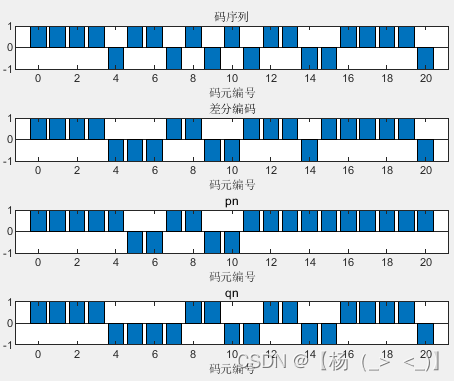
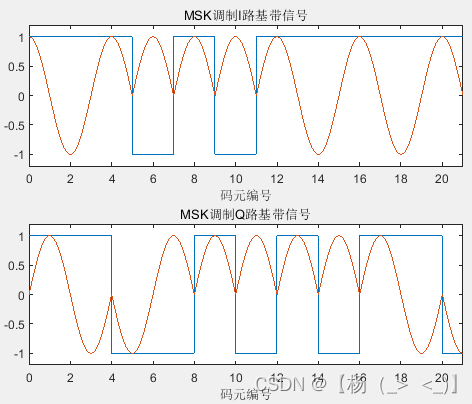
IQ两路码信号生成 MSK调制的基带IQ信号
左上图分别为双极化后的码,差分编码输出结果,MSK调制得到IQ两路码表示。右图是调制半个波特频率后的基带信号,可以看出
只在
为奇数的时候发生变化,
只在
为偶数时发生变化。
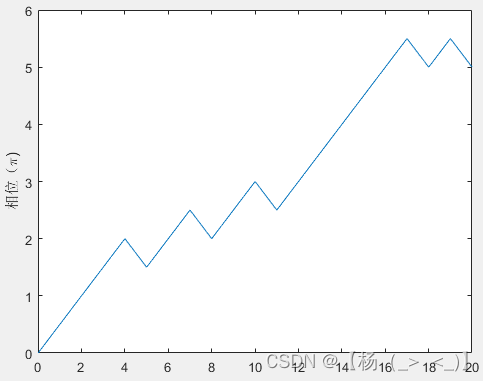
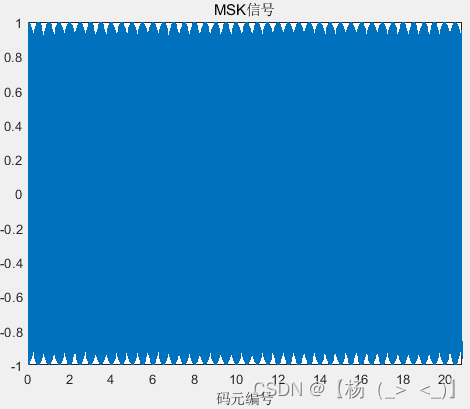
MSK基带信号的相位历程 MSK信号
左上图为MSK基带信号的相位历程,可以看出信号只有两种频率成分,且相位连续,右图是对应的MSK已调信号,信号基本横包络。
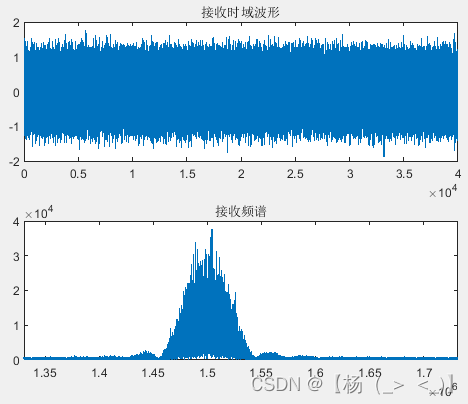
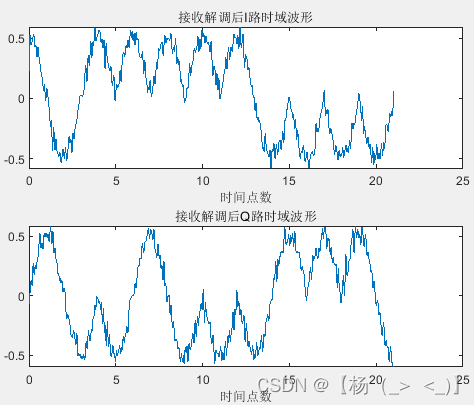
加噪的MSK信号 载波提取后的信号
上图为只考虑接收机热噪声影响下的接收信号以及载波提取后的信号,可以看出,噪声对信号产生了干扰,下图为对应的IQ两路信号的眼图,可以看出IQ两路信号存在码长大小的延时。
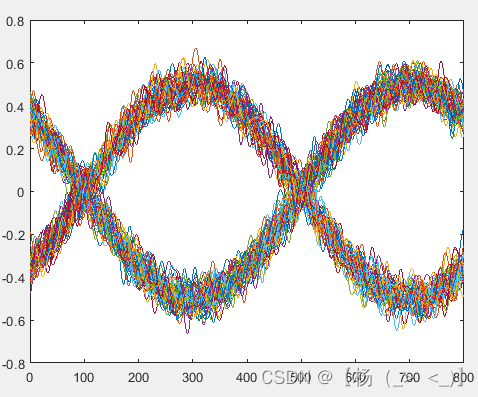
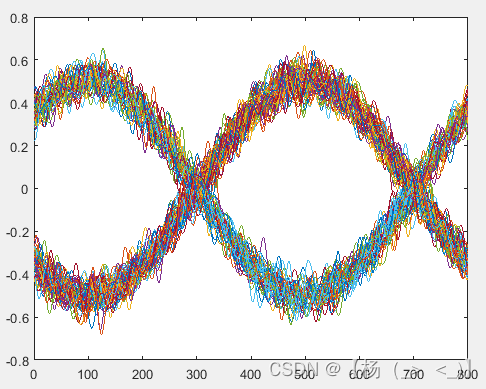
积分前I路眼图 积分前Q路眼图
对接收的IQ信号进行积分得到下图所示的眼图,可以看出眼图的展宽降低,对应的信噪比得到显著提升。
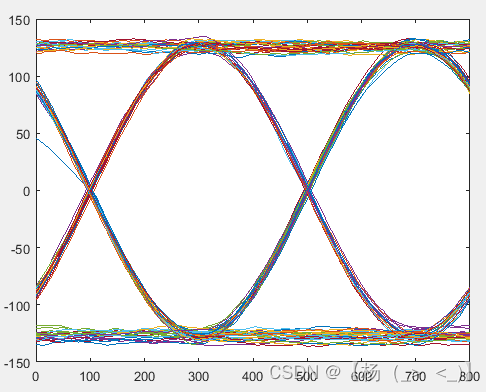
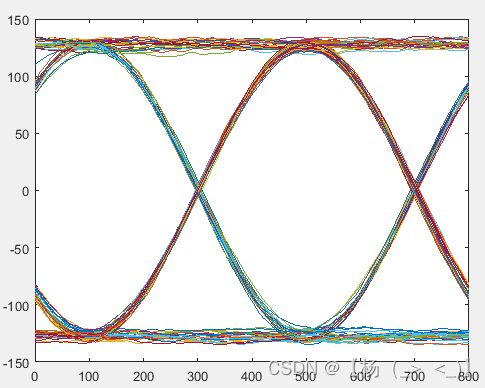
积分后I路眼图 积分后Q路眼图
最后分析了不同信号长度(1、2、4、10、100、1000符号长度)下的信号功率频谱与理论值的差异,可以看出随着信号长度增加,信号功率谱形状趋于公式(18)所示的功率谱形状。
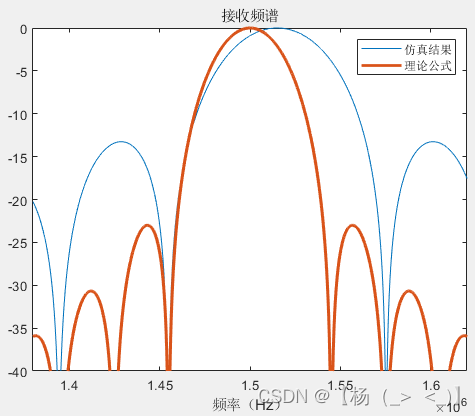
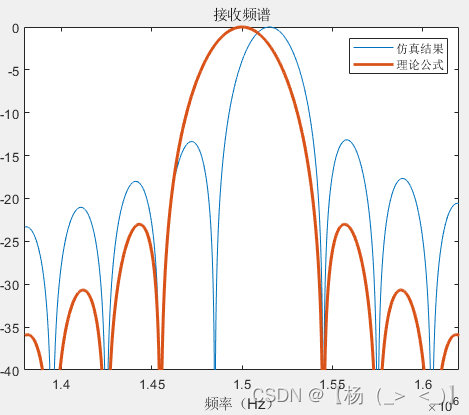
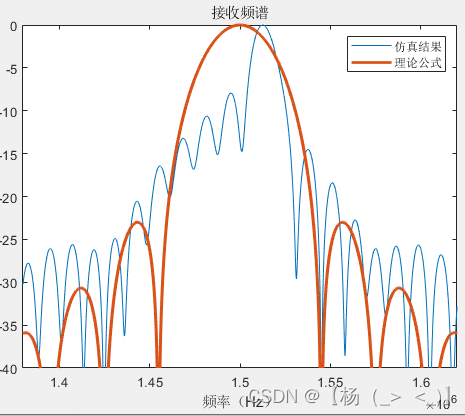
1 2 4
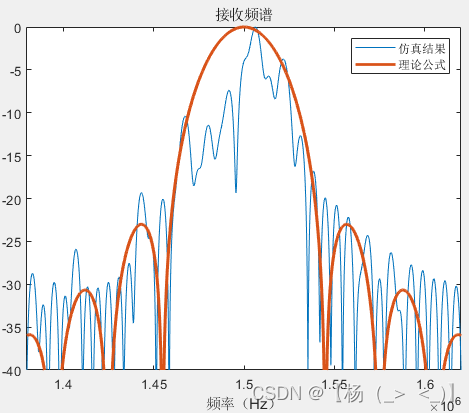
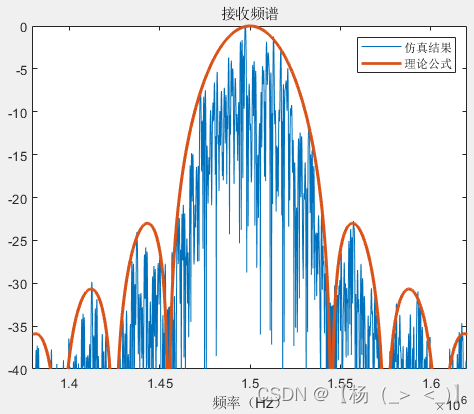
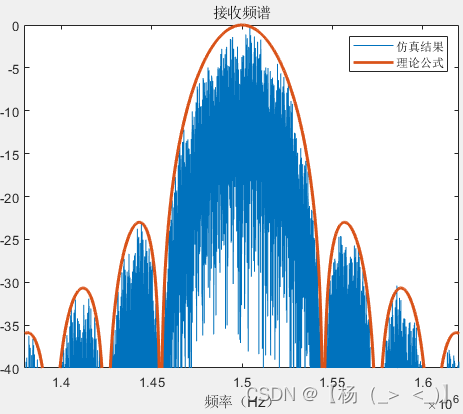
10 100 1000
参考文献
1、樊昌信 曹丽娜《通信原理》第7版
2、S. Gronemeyer and A. McBride, "MSK and Offset QPSK Modulation," in IEEE Transactions on Communications, vol. 24, no. 8, pp. 809-820, August 1976, doi: 10.1109/TCOM.1976.1093392.
总结
本文根据自己的理解从理论和仿真的角度介绍了MSK调制与解调原理,其中关于IQ路的延时处理可能和其他资料有所不同。有更好的内容欢迎在评论区放置链接,另外有问题也欢迎评论区留言。转载请附链接【杨(_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主
二周年纪念

目前《SAR学习笔记》观看量最多,有1.4w,阅读量过万的文章有两篇,另一篇《SAR学习笔记-SAR成像算法系列(一)》,阅读量过5千的文章有8篇,涉及:SAR,呼吸信号处理,Gold序列。整个创作,获得285次点赞,内容获得250次评论,获得1,843次收藏,代码片获得732次分享,资源总下载次数300多次。总阅读量14w。对于这样一个结果,博主还是很满意的。当然博主也欢迎各位看官有好的资源可以在评论区放置链接。根据目前情况,后期博主将对SAR领域中的干涉SAR、极化SAR、逆SAR内容进行补充。近期主要更新与信号类型有关的文章。当然,如果有什么信号处理的理论技术需要博主补充的可以评论区留言。
相关文章:

信号类型(通信)——最小频移键控(MSK)
系列文章目录 《信号类型(通信)——仿真》 《信号类型(通信)——QAM调制信号》 《信号类型(通信)——QPSK、OQPSK、IJF_OQPSK调制信号》 目录 前言 一、MSK信号特点 1.1、最小频移 1.2、相位连续 二…...

滴滴打车崩了!全过程
滴滴发布致歉10元补偿券,文末可领取 。 事情发生于 2023年11月27日晚~28日中午,滴滴打车服务出现大面积故障,登上微博热搜。 许多用户在使用滴滴出行时遇到了无法叫车、订单异常等问题,导致大量用户滞留在外,出行受阻…...
【刷题】DFS
DFS 递归: 1.判断是否失败终止 2.判断是否成功终止,如果成功的,记录一个成果 3.遍历各种选择,在这部分可以进行剪枝 4.在每种情况下进行DFS,并进行回退。 199. 二叉树的右视图 给定一个二叉树的 根节点 root&#x…...

Gin投票系统(2)
投票系统 数据库的建立 先分析需求,在sql中建立数据库,关于项目数据库如何建立可以在“goweb项目创建流程分析中看如何去建表” 成功后目前有四个表: vote,user,vote_opt,vote_opt_user 建立数据库,可以…...

docker (简介、dcoker详细安装步骤、容器常用命令)一站打包- day01
一、 为什么出现 Docker是基于Go语言实现的云开源项目。 Docker的主要目标是“Build,Ship and Run Any App,Anywhere”,也就是通过对应用组件的封装、分发、部署、运行等生命周期的管理,使用户的APP(可以是一个WEB应用或数据库应…...
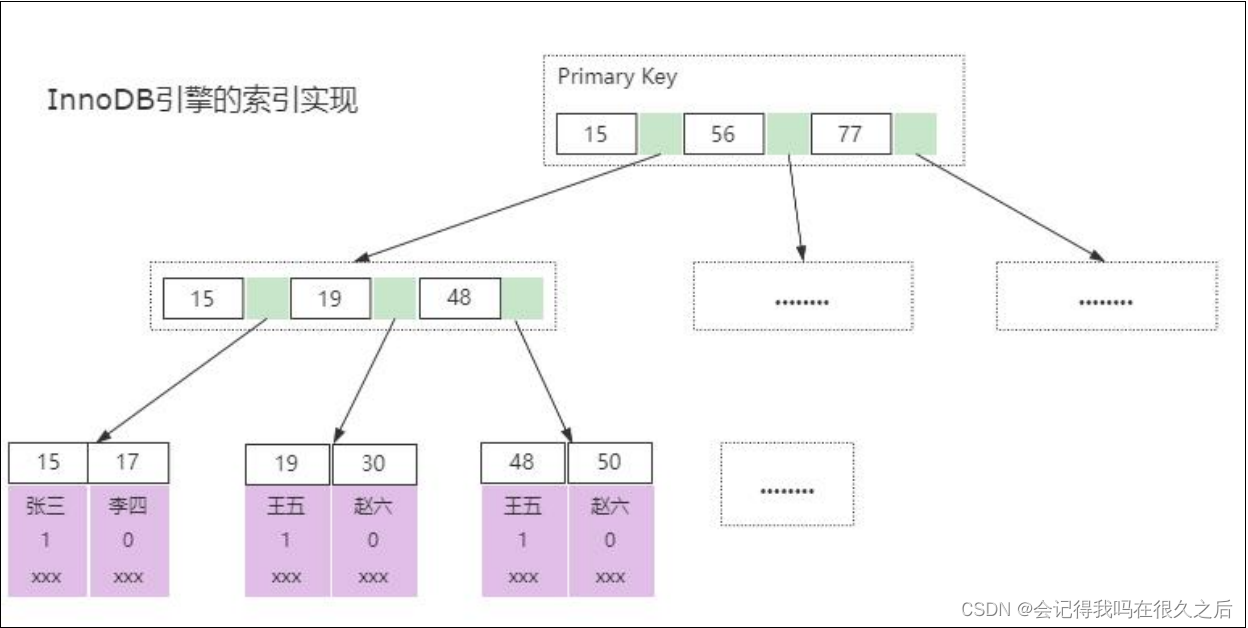
请简要说明 Mysql 中 MyISAM 和 InnoDB 引擎的区别
“请简要说明 Mysql 中 MyISAM 和 InnoDB 引擎的区别”。 屏幕前有多少同学在面试过程与遇到过类似问题, 可以在评论区留言:遇到过。 考察目的 对于 xxxx 技术的区别,在面试中是很常见的一个问题 一般情况下,面试官会通过这类…...

Nginx漏洞复现与分析
Nginx如何处理PHP请求 Nginx本身不支持直接解析和执行PHP代码,但可以通过与PHP解释器的集成来处理PHP请求。一种常见的方法是使用PHP-FPM(FastCGI Process Manager)作为PHP解释器。 原理图: Step 1 Step 2 +---------------------+ …...
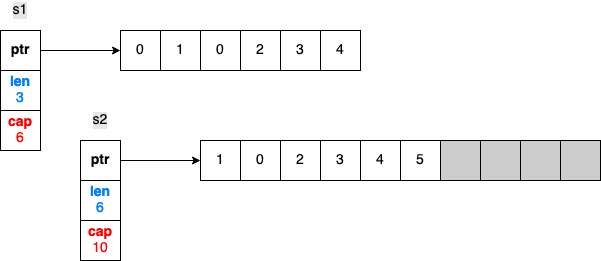
Go 中切片(Slice)的长度与容量
切片长度与容量在 Go 中很常见。切片长度是切片中可用元素的数量,而切片容量是从切片中第一个元素开始计算的底层数组中的元素数量。 Go 中的开发者经常混淆切片长度和容量,或者对它们不够了解。理解这两个概念对于高效处理切片的核心操作,比…...

顶级大厂Quora如何优化数据库性能?
Quora 的流量涉及大量阅读而非写入,一直致力于优化读和数据量而非写。 0 数据库负载的主要部分 读取数据量写入 1 优化读取 1.1 不同类型的读需要不同优化 ① 复杂查询,如连接、聚合等 在查询计数已成为问题的情况下,它们在另一个表中构…...

Java第二十章多线程
一、线程简介 线程是操作系统能够进行运算调度的最小单位,它被包含在进程之中,是进程中的实际运作单位。一个进程可以包含多个线程,这些线程可以并发执行。线程拥有自己的栈和局部变量,但是它们共享进程的其他资源,如…...

家庭教育,培养娃什么最重要?
家庭教育,培养娃什么最重要? 培养能力最重要 (我这么认为的) 时代巨变,技术变革的非常快,所以总的来说 年轻一代接触的新东西慢慢比老一代的要多,年轻一代的工作会比老一代的多而且多很多&…...
Linux 进程(一)
1 操作系统 概念:任何计算机系统都包含一个基本的程序集合,称为操作系统(OS)。笼统的理解,操作系统包括 内核(进程管理,内存管理,文件管理,驱动管理) 其他程序(例…...
vue中的keep-alive详解与应用场景
🌈个人主页:前端青山 🔥系列专栏:Vue篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来vue篇专栏内容:vue-keep-alive 目录 一、Keep-alive 是什么 二、使用场景 三、原理分析 四、案例实现 activa…...
软件设计师——程序设计语言基础(一)
📑前言 本文主要是【程序设计语言基础】——程序设计语言基础的相关题目,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是听风与他🥇 ☁️博客首页:CSDN主页听风与他 &#…...

Apache简介与安装
先导概念: 静态网站: 最早的建站方式,每个页面都是一个独立的文件,需要手动上传或编辑。网页内容固定不变。例如,个人博客、静态企业官网等。 动态网站: 网站内容可根据不同情况动态变更,一般通过数据库进行架构。包含服务器端脚本,可以实现更丰富的功能。例如,社…...

set与map
set与map 一、序列式容器与关联式容器二、pair1、键值对2、作用3、构造函数4、make_pair(1)构造函数(2)作用 5、代码6、运行结果 三、set1、概念2、代码3、运行结果4、说明 四、multiset1、与set的关系2、代码3、运行结果 五、map…...

基于单片机智能液位水位监测控制系统
**单片机设计介绍, 基于单片机智能液位水位监测控制系统 文章目录 一 概要特点应用场景工作原理实现方式 系统功能实时监测控制调节报警功能数据记录与分析 总结 二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 ## 系统介绍 基于单片机…...

C#,《小白学程序》第十七课:随机数(Random)第四,移动平均值(Moving Average)的计算方法与代码
1 文本格式 /// <summary> /// 《小白学程序》第十七课:随机数(Random)第四,移动平均值的计算方法与代码 /// 继续学习数据统计,移动平均值的计算方法 /// 移动平均值就是一定步长内数值的平均值,用…...
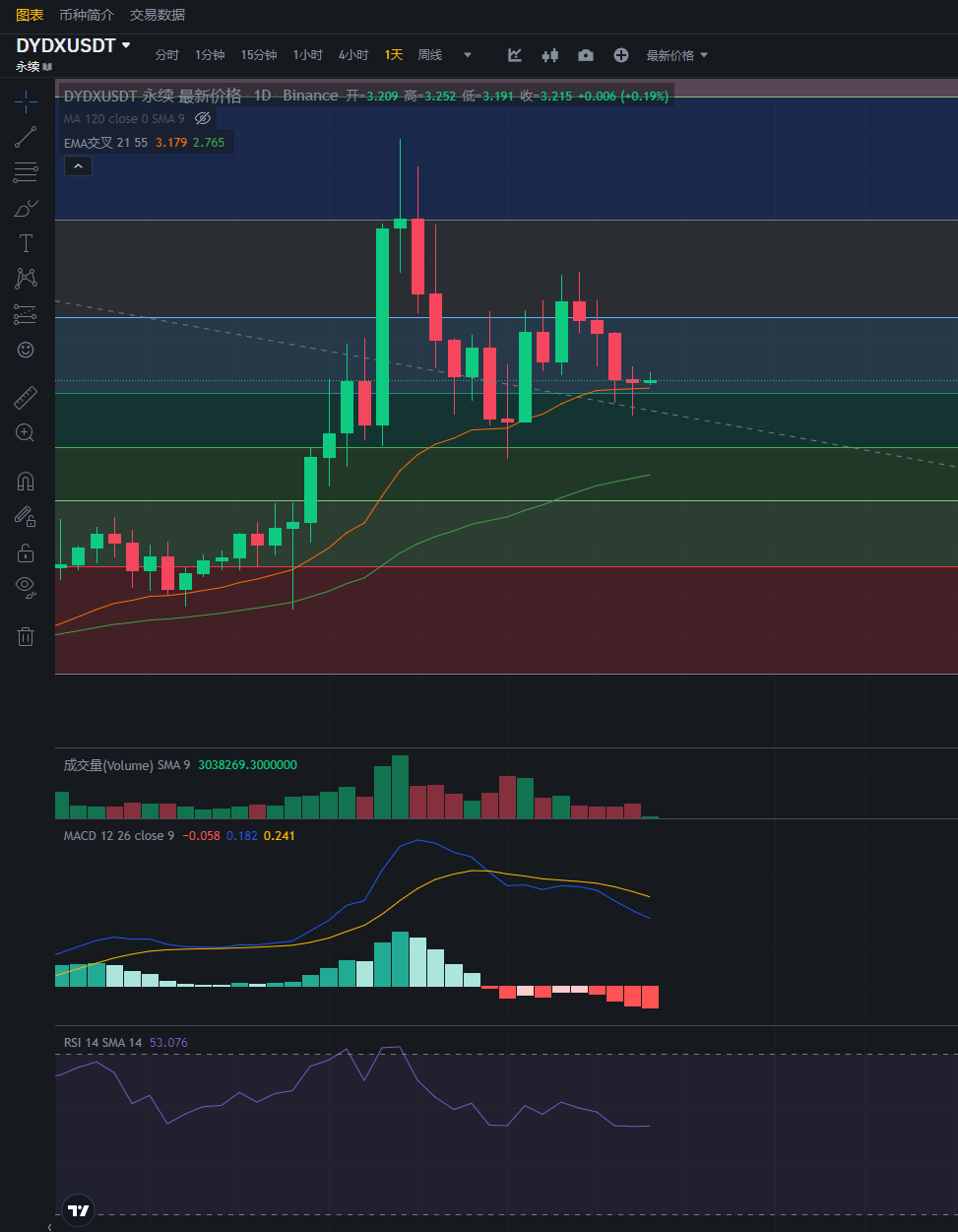
行情分析——加密货币市场大盘走势(11.29)
大饼已经形成了底背离,即MACD往下走,而价格还在往上走,这种后续往往会大跌。继续把空单拿好,已经持仓的无需加仓。多次上涨却一直不能突破,说明多空和空军力量都很强,等待后续出方向。在笔者看来࿰…...

C++——string的字符串比较,字符存取,插入和删除和子串
一. string字符串比较 功能描述:字符串之间的比较 比较方式:字符串比较是按字符的ASCII码进行对比 返回 0 > 返回 1 < 返回 -1 函数原型: *int compare(const string &s) const; //与字符串s比较 *int compare(const char *s) const; //…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...
