当前位置： 首页 > news >正文

索莫菲模型的一些理解 Smomerfeld Model

news 2026/2/10 21:51:50

 

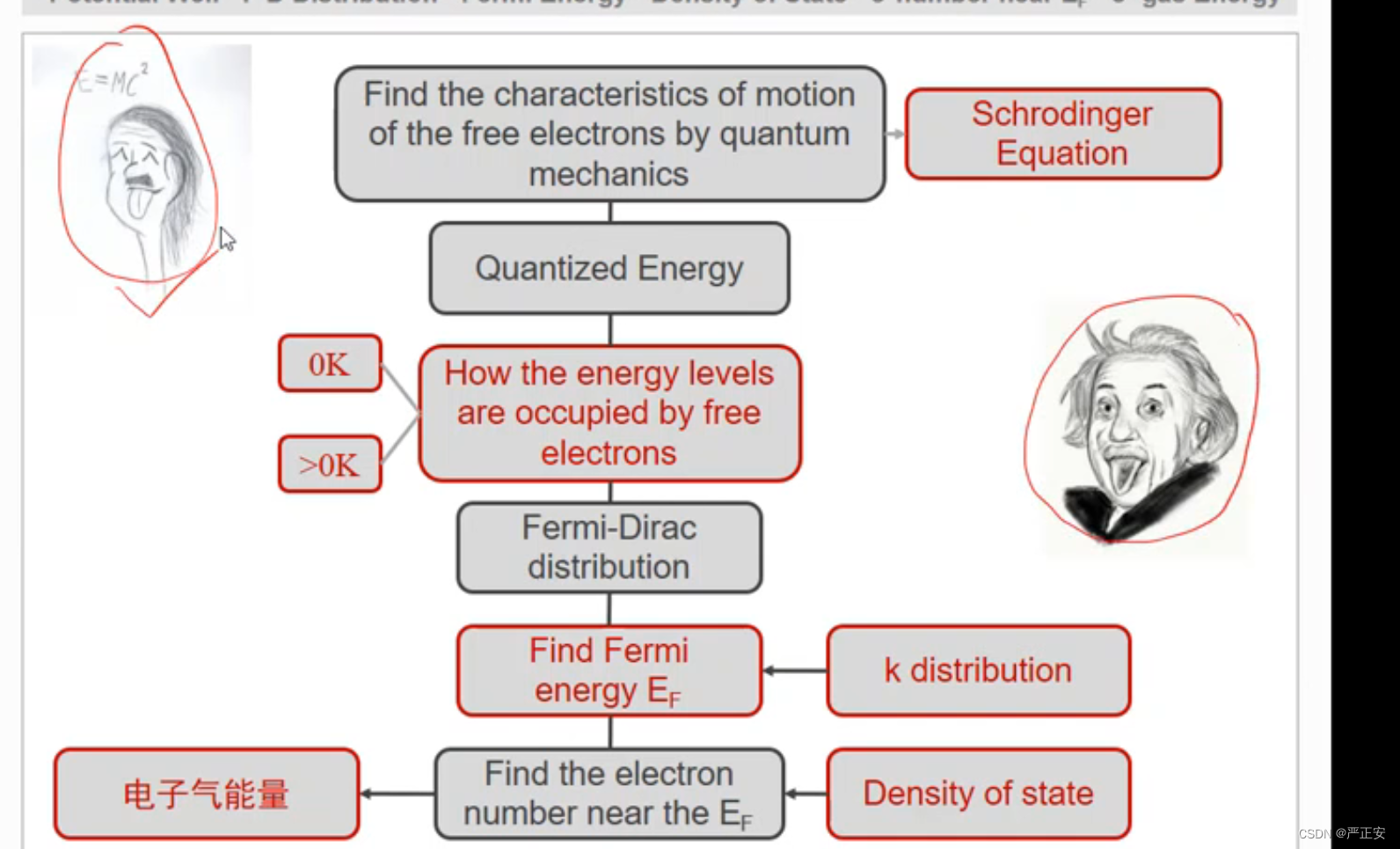
如何解释传统热容算出来的数值与量子模型下的区别？

CFE \ model \ predicts-> C_v =\frac{3}{2}R\\ \ \ experiments \ show -> C_v=10^{-4}RT

因为只有费米能附近的电子才能够进行移动，这个是问题的差别所在

我们下面就来介绍如何求费米能（费米能的计算）

既然费米能附近的电子很重要，那么附近的电子有多少很重要

我们需要波矢的分布和态密度

我们知道了

E=\frac{h^2 k^2}{2m}=\frac{h^2}{2m}(k_x^2+k_y^2+k_z^2) 

\vec k=k_x \vec i +k_y \vec j+k_z \vec l

k_x=\frac{2 \pi}{L} n_x,k_y=\frac{2 \pi}{L} n_y,k_z=\frac{2 \pi}{L} n_z

E=(n_x^2+n_y^2+n_z^2)E_0 =n^2 E_0,E_0=\frac{\pi^2 h^2}{2 m L^2}

如果落在一个球面上都具有相同的能量，K空间存在一个等能面

我们求解薛定谔方程的时候能量时量子化的

费米能在k空间的形状是一个球面，费米球的表面我们称之为费米面

费米球的半径称为费米波矢E_F=\frac{(hk_F)^2}{2m}

我们把

\rho (k)*V_{Fermi sphere}=N_{k}

\rho(k)=\frac{V}{8 \pi^3}

V_{F}\cdot \rho(k)=(\frac{4 \pi k_F^3}{3})(\frac{V}{8 \pi^3})=\frac{k_F^3}{6 \pi^2}V

Number \ of \ e^{-} N=2 \cdot \frac{k_F^3}{6 \pi^2}V

Density \ of \ e^{-} \ n=\frac{N}{V}=\frac{k_F^3}{3 \pi^2}

k_F = (3 \pi^2 n)^{\frac{1}{3}}

E_{F}^{0}=\frac{(\hbar k_F)^2}{2m}= \frac{ \hbar^2}{2m}(3 \pi^2 n)^{\frac{2}{3}}

n是自由电子密度，是一个本征量

 

我们下面找到费米能附近的电子数量，也就是电子随能量的分布情况

DOS:单位频率间隔独立格波的数目

在自由电子理论里面定义有所不同

DOS:单位能能量间隔电子的能态数量，用g(E)来表示

g(E)=\frac{dZ}{dE}

在半径k里面总的能态数量

Z(E)=2 \cdot \rho(k) \cdot \frac{4}{3} \pi k^3=\frac{Vk^3}{3 \pi^2}

g(E)=\frac{dZ}{dE}=\frac{dZ}{dk}\cdot \frac{dk}{dE}

g(E)=\frac{dZ}{dk}\cdot \frac{dk}{dE}=\frac{V}{ 2 \pi^2}\cdot \frac{2m}{\hbar^2}^{\frac{3}{2}} \cdot E^{\frac{1}{2}}

g(E)= C \cdot E^{\frac{1}{2}}

电子能量分布函数

N (E) 电子能量分布函数

N(E)=g(E) f(E)

g(E)是电子能态的数量，f(E)是占据该能态的概率

N=\int_{0}^{+\infty}g(E)f(E)dE

 

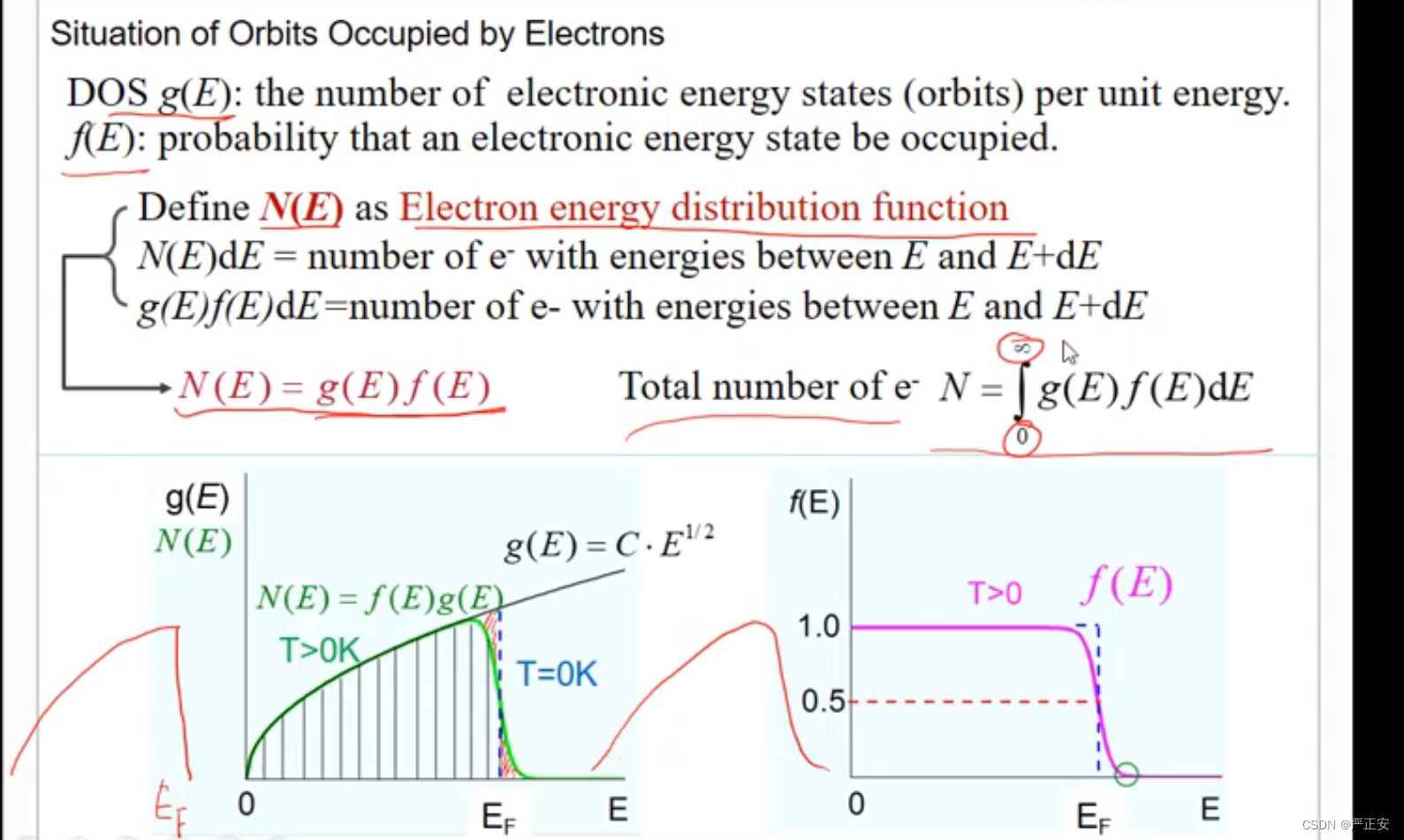
 T=0k的时候

E_t=\int E dN=\int E \cdot g(E) \cdot f(E)\cdot dE

=\frac{2C}{5}(E_F^0)^{\frac{5}{2}}

平均能量\overline E = \frac{3}{5} E_{F}^{0}

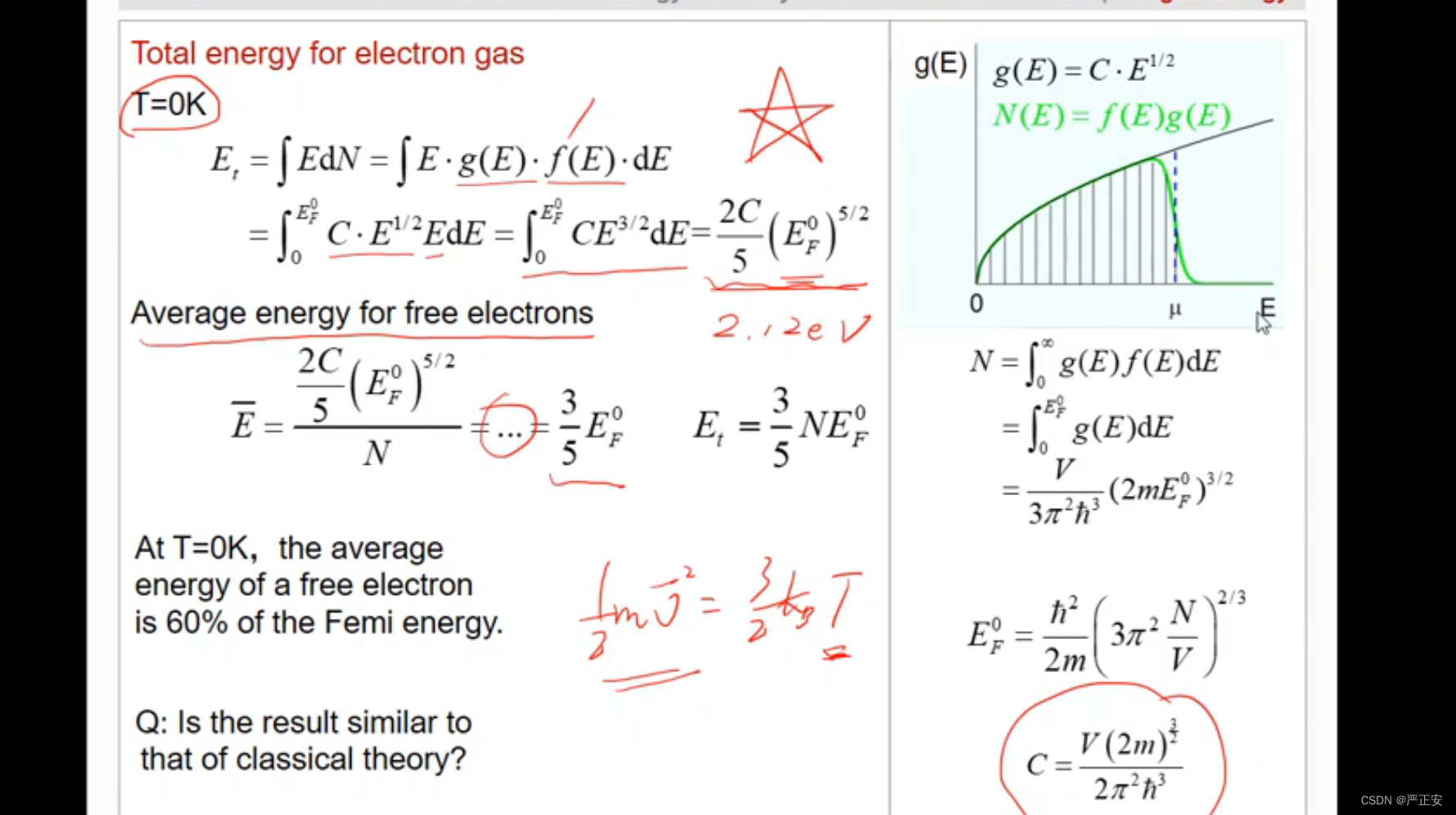
温度不为0k的时候，情况会变得稍微复杂一些

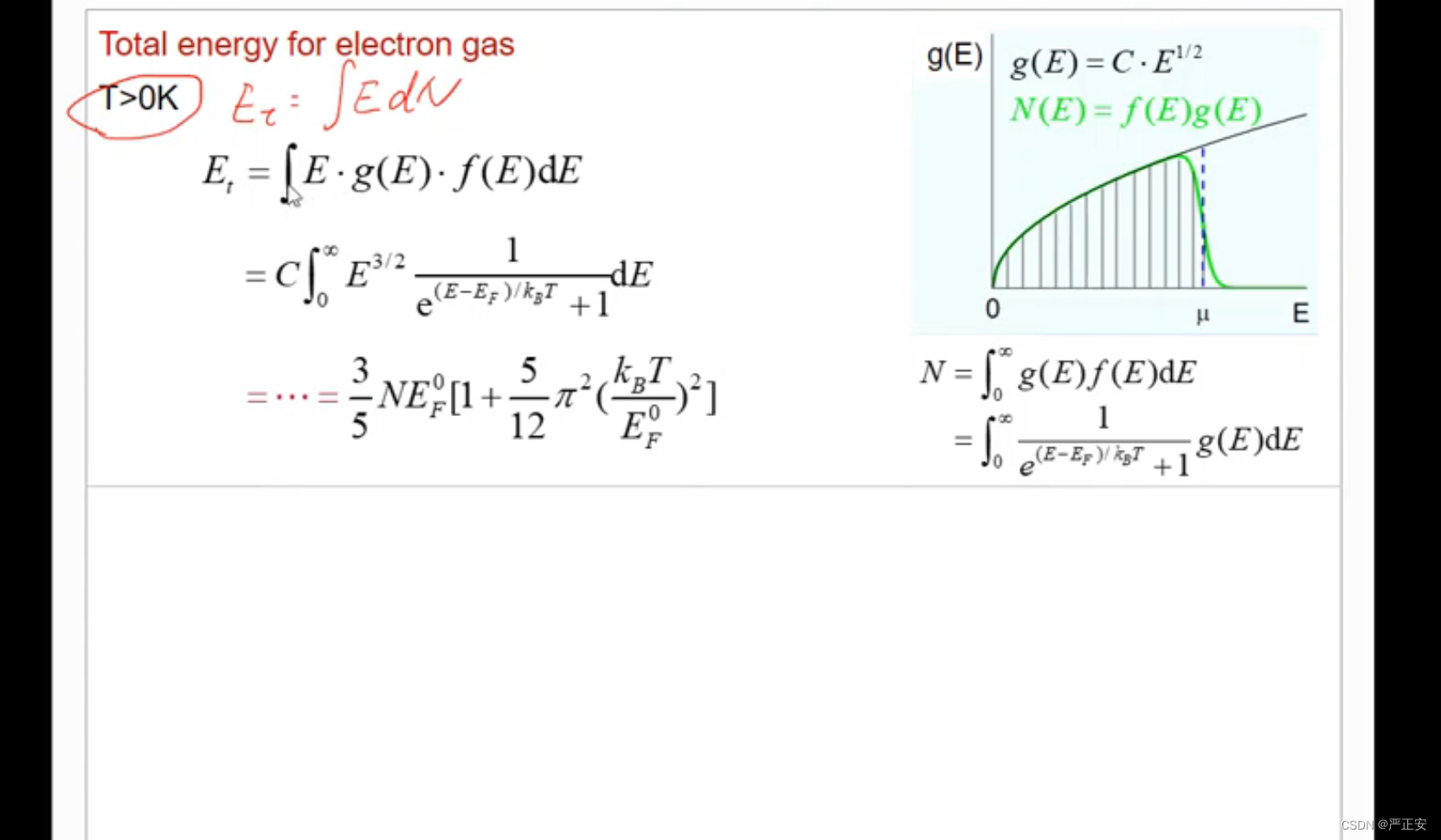
 我们可以把前面的称为零点能，随着温度的升高，电子气能量的增加都体现在后面的因子上面了

相关文章：

索莫菲模型的一些理解 Smomerfeld Model

如何解释传统热容算出来的数值与量子模型下的区别？ 因为只有费米能附近的电子才能够进行移动，这个是问题的差别所在 我们下面就来介绍如何求费米能（费米能的计算） 既然费米能附近的电子很重要，那么附近的电子有多少很…...

编程日记 2023/3/2 2:45:00

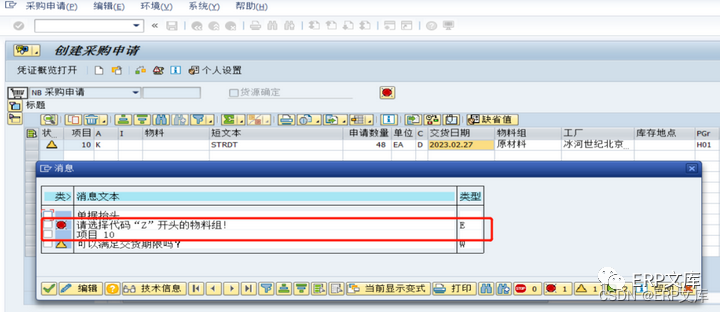
SAP ERP系统MM模块常用增强之四：采购申请输入字段的校验检查

在SAP/ERP项目的实施中采购管理模块（MM）的创建和修改采购申请一般都会有输入字段校验检查的需求，来防止业务人员录入错误或少录入数据，这方面需求部分是可以通过配置实现，比如一些字段是否必输，是否显示等&…...

编程日记 2023/3/2 2:43:54

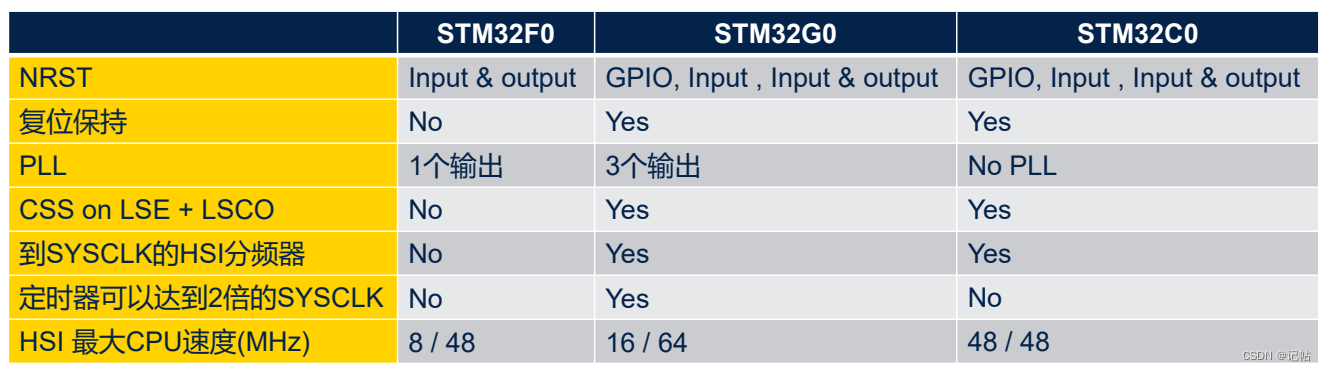
STM32C0介绍(1)----概述

概述 STM32C0系列微控制器是意法半导体公司推出的一款低功耗、高性能的微控制器产品。它们被设计用于需要小型、低功耗和高度可集成的应用程序，如传感器、消费品、电池供电设备、家庭自动化和安全等应用。该系列的微控制器采用ARM Cortex-M0内核，具有丰…...

编程日记 2023/3/2 2:42:48

windows无盘启动技术开发之传统BIOS(Legacy BIOS)引导程序开发之一

by fanxiushu 2023-03-01 转载或引用请注明原始作者。这个话题可能有点老，UEFI BIOS 已经大量存在，而Legacy BIOS最终会被取代。但是也是作为无盘启动技术里不可或缺的，毕竟还有许多老型号的电脑存在，而且为了兼容性，有…...

编程日记 2023/3/2 2:41:43

mysql实现if语句判断功能的六种使用形式

文章目录 前言一、ifnull函数二、nullif函数三、if函数四、if语句（多用于存储过程）五、if-else语句（多用于存储过程）六、if-elseif-else语句（多用于存储过程）总结前言 在Mysql数据库中实现判断功能有很多方式，具体又分为函数和if语句形式，函数的好处是可以作为sql的一…...

编程日记 2023/3/2 2:40:35

在Vue3这样子写页面更快更高效

前言 在开发管理后台过程中，一定会遇到不少了增删改查页面，而这些页面的逻辑大多都是相同的，如获取列表数据，分页，筛选功能这些基本功能。而不同的是呈现出来的数据项。还有一些操作按钮。 对于刚开始只有 1&#xff…...

编程日记 2023/3/2 2:39:28

做软件测试，如何才能实现月入20K？

听我的，测试想要月入20k。 首先你要去大厂，不在大厂起码也得在一线城市，北上广深。 二线城市的话成都、杭州最好。 不然的话想都不要想。 像我之前整理过成都的公司，除了字节跳动、蚂蚁金服、滴滴、美团、京东、平安、字节跳动…...

编程日记 2023/3/2 2:38:22

mysql last lesson

1:创建用户 create user zhang identified by 12345678;2：给用户授权，撤销授权， grant.......to revoke ....... 3:将数据库中的数据导出 C:\Windows\system32>mysqldump bjpowernode>C:\bjpowernode.sql -uroot -p12345678 4&#…...

编程日记 2023/3/2 2:37:16

一、Redis入门概述（是什么，能干嘛，去哪下，怎么玩）

一. redis是什么？ Redis:REmote Dictionary Server(远程字典服务器)官方解释： Remote Dictionary Server(远程字典服务)是完全开源的，使用ANSIC语言编写遵守BSD协议，是一个高性能的Key-Value数据库提供了丰富的数据结构&#xff…...

编程日记 2023/3/2 2:36:07

（六十二）当我们在SQL里进行分组的时候，如何才能使用索引？

今天我们接着上次的内容来谈谈在SQL语句里假设你要是用到了group by分组语句的话是否可以用上索引，因为大家都知道，有时候我们会想要做一个group by把数据分组接着用count sum之类的聚合函数做一个聚合统计。 那假设你要是走一个类似select count(*) fr…...

编程日记 2023/3/2 2:35:00

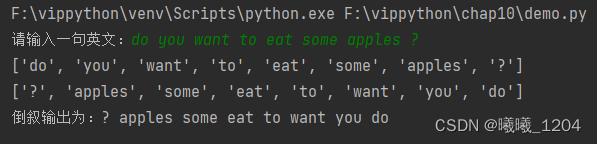
python字符串练习

python字符串练习 1.去掉字符串中所有的空格 s This is a demo print(s.replace( , )) 2.获取字符串中数字的个数 data input("请输入一些字符串：") a 0 for i in data:if i.isdigit():a a 1 print("数字个数:", a)3.将字母全部转换为…...

编程日记 2023/3/2 2:33:55

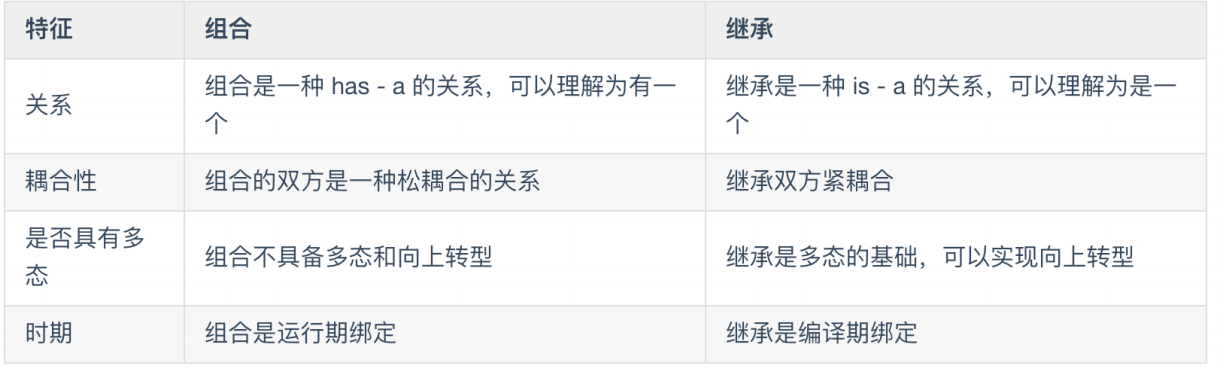
Java-封装、继承、多态

封装 访问控制权限又成为“封装”，是面向对象三大特征中的一种。核心是，只对需要的类可见。 继承 继承是所有OOP（Object Oriented Programming）语言和Java语言都不可或缺的一部分。 只要创建一个类，就隐式继承自Obje…...

编程日记 2023/3/2 2:32:47

问题三十二：离散二维傅立叶变换（Discrete Fourier Transformation）

为了将灰度图像表示为频谱图，我们需要进行以下步骤： 加载图像并将其转换为灰度图像。对图像进行二维离散傅里叶变换。将变换结果表示为幅度谱和相位谱。可以对幅度谱和相位谱进行可视化，以查看频率分布。对幅度谱和相位谱进行逆变换&#xf…...

编程日记 2023/3/2 2:31:40

恢复谷歌翻译的究极方法

谷歌翻译为什么会失效，我想各位在去年11月的时候就知道了。可是要怎么解决失效的问题呢？之前我们是通过手动Ping可以连接的ip各位可能觉得麻烦，心里觉得什么档次还要我手动ping就没有可以自动扫描的吗？还别说真的有我最近发现一个…...

编程日记 2023/3/2 2:30:32

string函数以及string常用接口

本文介绍的是C关键字string中一些重要用法，以及各种字符串序列的处理操作 ——飘飘何所似，天地一沙鸥 文章目录前言一、string（字符串类）二、string类对象的容量操作2.1 size/length2.2 capacity2.3 empty/clear2.4 resize/reser…...

编程日记 2023/3/2 2:29:20

分享一篇由C语言实现《数据结构》无头无循环单链表

三月，你好，各位csdn uu们好 文章目录前言一、何为单链表二、单链表基本操作（增，删，查，改，销毁，遍历）1.查找与修改、销毁与遍历2.链表插入与删除操作三、单链表 VS 顺序表…...

编程日记 2023/3/2 2:28:14

C盘爆满？两个超简单的解决办法

我们在使用电脑的过程中，经常容易出现C盘爆红，反而其他盘还有大量可用空间的情况。为什么会这样呢？其实主要就两种原因：一是电脑使用习惯不好，不管什么软件都默认安装在C盘，大文件又喜欢放在桌面&#xff0…...

编程日记 2023/3/2 2:27:08

ThreadLocal

ThreadLocalThreadLocalMapgetsetremove内存泄漏key用强/弱引用entry继承了弱引用ThreadLocal 一个对象的所有线程会共享其全局变量——>线程不安全 解决方式： 方式一：同步机制，加锁（时间换空间） 方式二&#xff1a…...

编程日记 2023/3/2 2:25:52

Java基础:JDK7-时间Date

JDK7以前时间相关类 1.Date Date date new Date(); , sout(date)得到的是现在所处位置的时间 Date date new Date(0L); , sout(date)得到的是时间原点也就是1970年1月1日08:00(东八区). date.setTime(1000L); sout(date)得到的是时间原点后一秒钟的时间 long time date.g…...

编程日记 2023/3/2 2:24:37

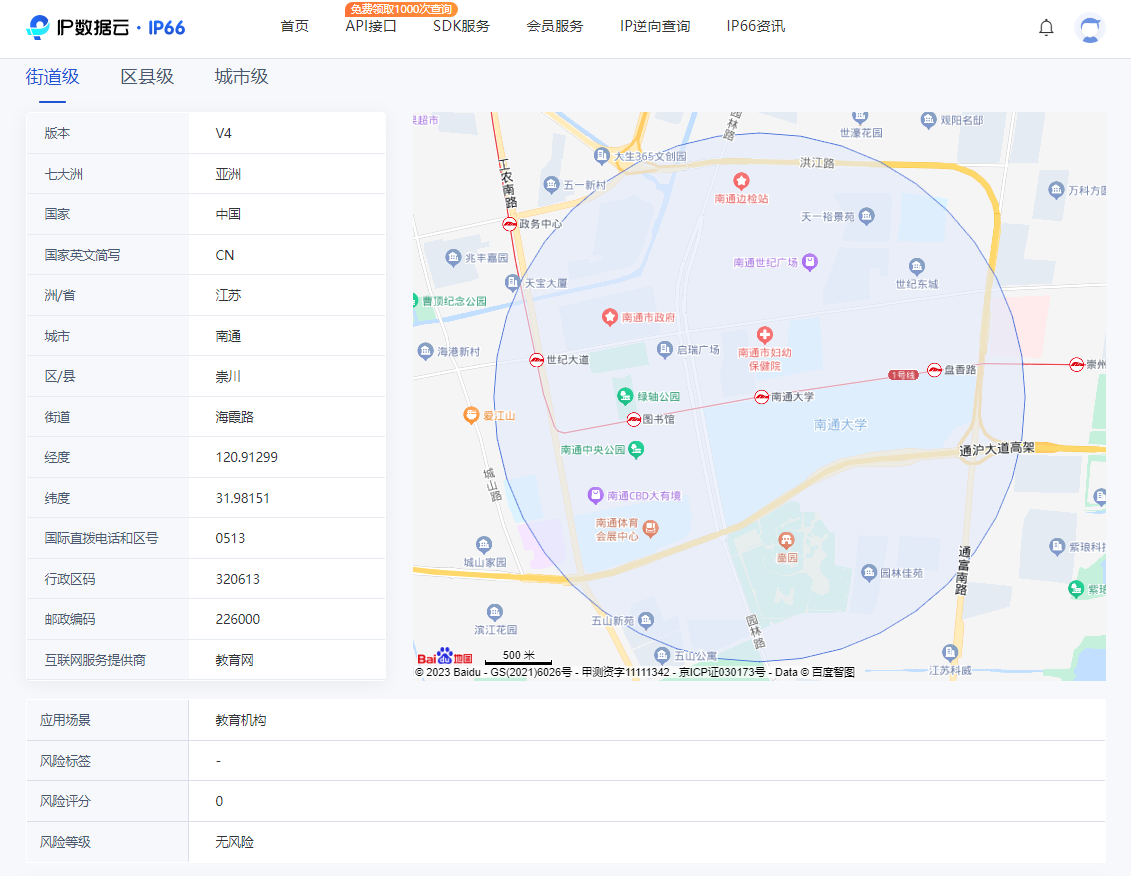
什么是IP地址？

IP协议中还有一个非常重要的内容，那就是给因特网上的每台计算机和其它设备都规定了一种地址，叫做“IP 地址”。由于有这种地址，才保证了用户在连网的计算机上操作时，能够高效而且方便地从千千万万台计算机中选出自己所需的对象来。…...

编程日记 2023/3/2 2:23:16

阿里云ACP云计算备考笔记 (5)——弹性伸缩

目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

编程新知 2026/1/22 6:07:24

Docker 运行 Kafka 带 SASL 认证教程

Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明：server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

编程新知 2026/1/23 4:15:03

linux 错误码总结

1，错误码的概念与作用 在Linux系统中，错误码是系统调用或库函数在执行失败时返回的特定数值，用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递，errno由操作系统维护，保存最近一次发生的错误信息。值得注意的是，errno的值在每次系统调用或函数调用失败时…...

编程新知 2025/9/16 22:48:47

srs linux

下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935，SRS管理页面端口是8080，可…...

编程新知 2026/2/6 9:49:55

今日科技热点速览

🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售，主打更强图形性能与沉浸式体验，支持多模态交互，受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

编程新知 2025/11/20 14:26:29

SpringTask-03.入门案例

一.入门案例 启动类： package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

编程新知 2026/2/2 0:35:08

安宝特案例丨Vuzix AR智能眼镜集成专业软件，助力卢森堡医院药房转型，赢得辉瑞创新奖

在Vuzix M400 AR智能眼镜的助力下，卢森堡罗伯特舒曼医院（the Robert Schuman Hospitals, HRS）凭借在无菌制剂生产流程中引入增强现实技术（AR）创新项目，荣获了2024年6月7日由卢森堡医院药剂师协会&#xff0…...

编程新知 2026/2/9 2:41:28

tomcat指定使用的jdk版本

说明 有时候需要对tomcat配置指定的jdk版本号，此时，我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

编程新知 2025/6/10 21:11:28

前端中slice和splic的区别

1. slice slice 用于从数组中提取一部分元素，返回一个新的数组。 特点： 不修改原数组：slice 不会改变原数组，而是返回一个新的数组。提取数组的部分：slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

编程新知 2025/11/27 20:15:13

【SpringBoot自动化部署】

SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一，能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时，需要添加Git仓库地址和凭证，设置构建触发器（如GitHub…...

编程新知 2025/11/18 2:17:20