蓝桥杯ACwing习题
题目 :https://www.acwing.com/problem/content/4409/
解析 :根据题目我们可以知道 问的是方案数 那么首先就想到了 dp 仔细想一下 发现类似于蒙德里安的梦想那道状态压缩的题 , 所以我们先考虑怎么定义 f[i][j]
f[i][j] 表示的是 已经放了前 i 行 且第 i + 1 填满了 j 个格子 , 由此我们画图可以知道
f[i][0] = f[i - 1][2 ] + f[i - 1][0]
f[i][1] = f[i - 1][1] + f[i - 1][0] * 2;
f[i][2] = f[i - 1][0] +f[i - 1][1];
矩阵用于解决大数据问题
设Fi = { fi0 , fi1 , fi2};
Fi -1= { fi - 10 , fi - 11 , fi - 12}:
Fi- 1 * A = Fi
由上面的可以得到
A = 1 2 1
0 1 1
1 0 0
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e7 + 10 , mod = 1e9 + 7;
typedef long long LL;
int dp[N][3]; // 已经放好了前 i 列 , 且第 i + 1 列放了 0 1 2 个的方案数
void mul(LL f[] , LL a[] , LL b[][3])
{
LL temp[3] = {0};
for(int i = 0 ; i < 3 ; i ++)
for(int j = 0 ; j < 3 ; j ++)
temp[i] = (temp[i] + a[j] * b[j][i]) % mod;
memcpy(f , temp ,sizeof temp);
}
void mul(LL a[3][3] , LL b[3][3] , LL c[3][3])
{
LL temp[3][3] = {0};
for (int i = 0; i < 3 ; i ++)
for (int j = 0; j < 3 ; j ++)
for (int k = 0; k < 3 ; k ++)
temp[i][j] = (temp[i][j] + a[i][k] * b[k][j]) % mod;
memcpy(a , temp , sizeof temp);
}
int main()
{
int n;
cin >> n;
// 求 dp[n][0] ?
n --;
LL a[][3] = {{ 1, 2, 1 },
{ 0 ,1 ,1 },
{ 1,0 ,0 }};
LL f[] = {1 , 2 , 1};
while (n)
{
if(n & 1) mul(f , f , a);
n >>= 1;
mul(a , a , a);
}
cout << f[0] << endl;
return 0;
}
相关文章:

蓝桥杯ACwing习题
题目 :https://www.acwing.com/problem/content/4409/ 解析 :根据题目我们可以知道 问的是方案数 那么首先就想到了 dp 仔细想一下 发现类似于蒙德里安的梦想那道状态压缩的题 , 所以我们先考虑怎么定义 f[i][j] f[i][j] 表示的是 已经放了…...
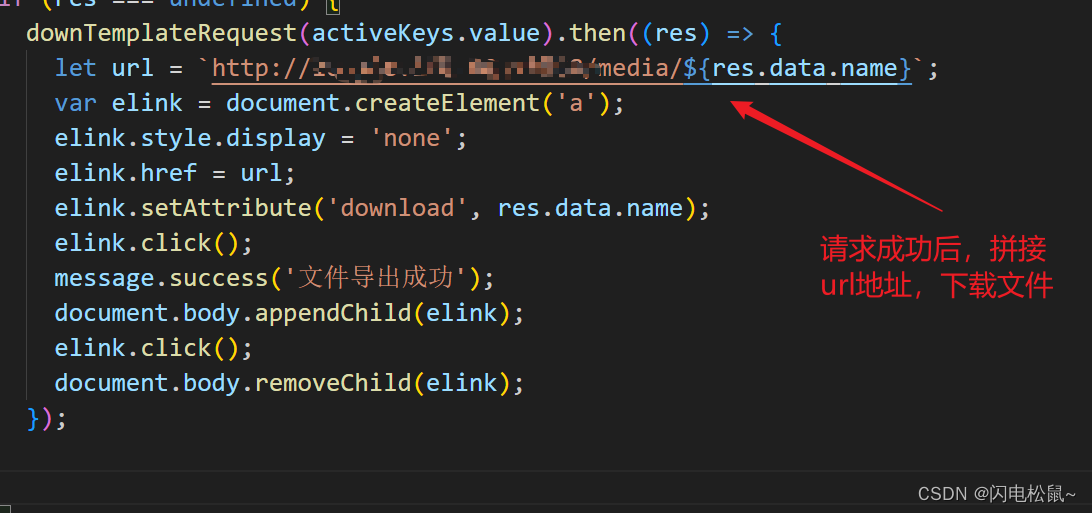
vue发送请求携带token,拼接url地址下载文件
封装请求 ,该请求为普通的get请求 该请求返回值为: 请求成功之后拼接URL地址下载文件 代码块 downTemplateRequest(activeKeys.value).then((res) > {let url http://47.169.168.99:18888/media/${res.data.name};var elink document.createElemen…...

【PTA-C语言】编程练习3 - 循环结构Ⅱ
如果代码存在问题,麻烦大家指正 ~ ~有帮助麻烦点个赞 ~ ~ 编程练习3 - 循环结构(9~15) 7-9 特殊a串数列求和(分数 15)7-10 穷举法搬运砖块问题(分数 15)7-11 数字金字塔(分数 15&…...
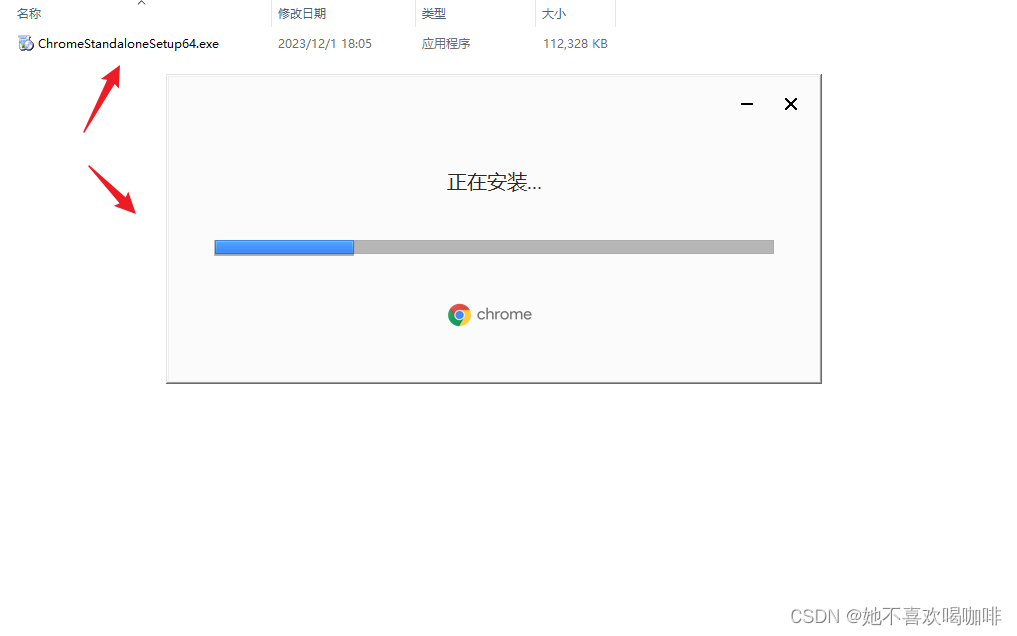
Google Chrome 下载 (离线版)
1 访问网址 Google Chrome 网络浏览器 2 点击 下载Chrome 3 直接运行 ChromeStandaloneSetup64.exe 其他: ####################### 谷歌浏览器 (Google Chrome) 最新版离线安装包下载 https://www.iplaysoft.com/tools/chrome/#google_vignette Google Chrome …...

2023年GopherChina大会-核心PPT资料下载
一、峰会简介 自 Go 语言诞生以来,中国便是其应用最早和最广的国家之一,根据 Jetbrains 在 2021 年初做的调查报告,总体来说目前大概有 110 万专业的开发者 选择 Go 作为其主要开发语言。就其全球分布而言, 居住在亚洲的开发者最多ÿ…...

从源代码出发,Jenkins 任务排队时间过长问题的解决过程
最近开发了一个部署相关的工具,使用 Jenkins 来构建应用。Jenkins 的任务从模板中创建而来。每次部署时,通过 Jenkins API 来触发构建任务。在线上运行时发现,通过 API 触发的 Jenkins 任务总是会时不时在队列中等待较长的时间。某些情况下的…...

openssl 生成CA及相关证书
实验环境:ubuntu18.04-desktop 获取openssl.cnf配置文件 # 这个返回的路径,不一定被使用了(经测试,ubuntu18下的openssl似乎未加载任何配置文件) openssl version -d生成私钥文件(pem) # 生成私钥 # genrsa…...

App测试之App日志收集及adb常用命令
文章目录 前言一、adb是什么1.APP测试收集手机日志常用的工具2.adb下载与安装3.ADT/SDK/ADB是什么4.adb连接真机 二、adb常用命令三、android系统日志文件1.logcat日志文件2.logcat日志文件分析 四、分析crash & ANR 日志1.发生crash如何分析2.发生ANR如何分析 总结扩展&am…...

【Java面试——并发基础、并发关键字】
3.1 并发基础 Java 并发 - 理论基础Java 并发 - 线程基础 多线程的出现是要解决什么问题的? 本质什么? CPU、内存、I/O 设备的速度是有极大差异的,为了合理利用 CPU 的高性能,平衡这三者的速度差异,计算机体系结构、操作系统、编译程序都…...
如何使用 Java 在Excel中创建下拉列表
下拉列表(下拉框)可以确保用户仅从预先给定的选项中进行选择,这样不仅能减少数据输入错误,还能节省时间提高效率。在MS Excel中,我们可以通过 “数据验证” 提供的选项来创建下拉列表,但如果要在Java程序中…...
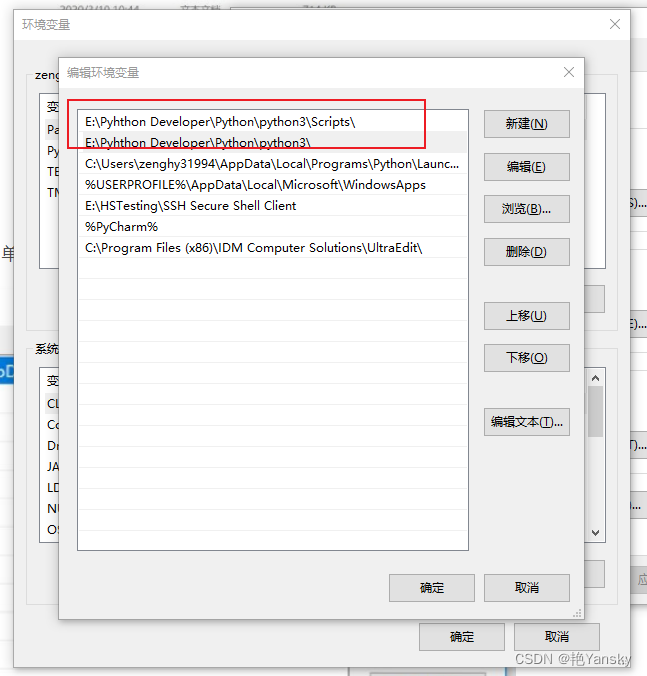
Python安装步骤介绍
本文将介绍Python安装的详细步骤如下: 下载 python安装 python配置环境变量(安装时勾选配置环境变量的则无需此步骤) 一、python下载 官网:Download Python | Python.org 根据电脑位数下载所需的版本 二、Python安装 1.打开安…...
笔记)
学习80min快速了解大型语言模型(ChatGPT使用)笔记
学习李宏毅:80min快速了解大型语言模型(ChatGPT使用)笔记 链接:https://www.youtube.com/watch?vwG8-IUtqu-s 1、创建一个属于自己的GPT 目前,GPT4具备一个功能,Create a GPT。利用这个功能可以创建一个…...

SQL错题集1
1.找出选修课程成绩最差的选课记录 注: 聚合函数只能用在group by和()括号中 找最值可用排序order bylimit 1 2. 查询选修成绩 合格的课程 超过2门的 学生编号 3.删除姓名为"LiMing"的学生信息 注: 删除一整行信息&…...

uniapp运行到安卓基座app/img标签不显示
img是html中的标签,他也是一个单标签 image属于服务器控件,是个双标签 问题:uniapp运行到app安卓基座后图片无法显示 原因:自己使用了img标签,而且输入路径无提示,img标签导致图片不显示 解决ÿ…...
vscode非常好用的扩展插件
1、Code Spell Checker: 帮助我们检查单词是否拼写错误,检查规则遵循驼峰拼写法。 2、Color Highlight:高亮显示颜色值 3、Svg Preview: 实时预览svg图片(修改width、height、fill等值来实时查看效果) 4、…...

一文弄懂BFS【广度优先搜索(Breadth-First Search)】
BFS,全名为广度优先搜索(Breadth-First Search),是一种用于图或树的遍历或搜索的算法。它的主要思想是由节点自身开始向它的邻居节点新进展开搜索,因此也常被形象地称为“层序遍历”。 BFS 基本思想 BFS 工作原理是,从开始节点开…...

深度学习记录--logistic回归函数的计算图
计算图用于logistic回归函数 先回顾一下单一样本的logistic回归损失函数的公式,公式如下: 将logistic函数用计算图表示出来(以两个基础量为例),计算图如下: 前向传播已经完成,接下来完成后向传播 运用链式法则依次求…...

Java基本数据类型详解
✨个人主页:全栈程序猿的CSDN博客 💨系列专栏:Java从入门到精通 ✌座右铭:编码如诗,Bug似流星,持续追求优雅的代码,解决问题如同星辰般自如 Java是一种强类型语言,数据类型在程序中起…...

第十五届蓝桥杯模拟赛(第二期)
大家好,我是晴天学长,本次分享,制作不易,本次题解只用于学习用途,如果有考试需要的小伙伴请考完试再来看题解进行学习,需要的小伙伴可以点赞关注评论一波哦!后续会继续更新第三期的。Ǵ…...

命令模式-C++实现
命令模式是一种行为型设计模式,它将请求封装成一个对象,从而能使你可以用不同的请求对客户端进行参数化。该模式允许请求的发送者和接收者进行解耦,发送者不需要知道接收者的信息,只需要通过命令对象来与它进行交互。 命令模式有…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
