12.04 二叉树中等题
513. 找树左下角的值
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:
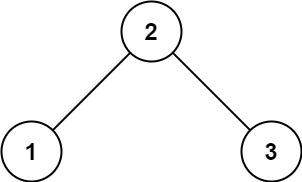
输入: root = [2,1,3] 输出: 1
思路:找到最低层中最左侧的节点值,比较适合层序遍历,返回最低层的第一个值即可。
细节:判断是否是最低层,需要保存节点的当前层数。可以用queue<pair>来保存pair保存<节点指针,层数>
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int findBottomLeftValue(TreeNode* root) {if(!root) return -1;queue<pair<TreeNode*,int>> q;q.push({root,1});int deepthMax=1;int ret=root->val;while(!q.empty()){pair<TreeNode*,int> pariFront=q.front();TreeNode* nodeFront=pariFront.first;int deepth=pariFront.second;//判断是否是更低的一层if(deepth>deepthMax){deepthMax=deepth;ret=nodeFront->val;}q.pop();if(nodeFront->left) q.push({nodeFront->left,deepth+1});if(nodeFront->right) q.push({nodeFront->right,deepth+1});}return ret;}
};-
时间复杂度:O(n),其中 nnn 是二叉树的节点数目。
654. 最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:

输入:nums = [3,2,1,6,0,5] 输出:[6,3,5,null,2,0,null,null,1] 解释:递归调用如下所示: - [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。- 空数组,无子节点。- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。- 空数组,无子节点。- 只有一个元素,所以子节点是一个值为 1 的节点。- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。- 只有一个元素,所以子节点是一个值为 0 的节点。- 空数组,无子节点。
思路:最简单的方法是直接按照题目描述进行模拟。
左子树为 construct(nums,left,best−1)
右子树为 construct(nums,best+1,right)
当递归到一个空数组时,便可以返回一棵空的树。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int findMaxIndex(vector<int>& nums){int ret=0;for(int i=1;i<nums.size();i++){if(nums[i]>nums[ret]) ret=i;}return ret;}TreeNode* constructMaximumBinaryTree(vector<int>& nums) {if(nums.empty()) return nullptr;int maxIndex=findMaxIndex(nums);vector<int> leftNums(nums.begin(),nums.begin()+maxIndex);vector<int> rightNums(nums.begin()+maxIndex+1,nums.end());TreeNode* root=new TreeNode(nums[maxIndex],constructMaximumBinaryTree(leftNums), //左子树constructMaximumBinaryTree(rightNums)); //右子树return root;}
};时间复杂度:O(n^2),其中 nnn 是数组 nums\textit{nums}nums 的长度。在最坏的情况下,数组严格递增或递减,需要递归 n 层,第 i (0≤i<n)层需要遍历 n−i个元素以找出最大值,总时间复杂度为 O(n2)
思路2:利用单调栈可以实现时间复杂度O(n)
代码随想录
相关文章:

12.04 二叉树中等题
513. 找树左下角的值 给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。 假设二叉树中至少有一个节点。 示例 1: 输入: root [2,1,3] 输出: 1 思路:找到最低层中最左侧的节点值,比较适合层序遍历,返回最…...

Redis的安装
本文采用原生的方式安装Redis,Redis的版本为5.0.5 安装 下载 下载网站:https://download.redis.io/releases/ wget http://download.redis.io/releases/redis-5.0.5.tar.gz解压 tar -zxvf redis-5.0.5.tar.gz进入redis目录 cd redis-5.0.5执行编译…...
JDK安装太麻烦?一篇文章搞定
JDK是 Java 语言的软件开发工具包,主要用于移动设备、嵌入式设备上的java应用程序。JDK是整个java开发的核心,它包含了JAVA的运行环境(JVMJava系统类库)和JAVA工具。 JDK包含的基本组件包括: javac – 编译器…...

漫谈HBuilderX App-Jenkins热更新构建
漫谈Uniapp App热更新包-Jenkins CI/CD打包工具链的搭建 零、写在前面 HBuilderX是DCloud旗下的IDE产品,目前只提供了Windows和Mac版本使用。本项目组在开发阶段经常需要向测试环境提交热更新包,使用Jenkins进行CD是非常有必要的一步。尽管HBuilderX提…...

技术前沿丨Teranode如何实现无限扩容
发表时间:2023年9月15日 BSV区块链协会的技术团队目前正在努力开发Teranode,这是一款比特币节点软件,其最终目标是实现比特币的无限扩容。然而,正如BSV区块链协会网络基础设施负责人Jake Jones在2023年6月举行的伦敦区块链大会…...

世岩清上:如何制作年终工作汇报宣传片
年终工作汇报宣传片是一种以视觉和口头语言为主要表现形式的宣传手段,旨在向领导、同事、客户等展示一年来的工作成果和亮点。以下是制作年终工作汇报宣传片的几个关键步骤: 明确目的和受众:在制作宣传片前,要明确宣传片的目的和受…...
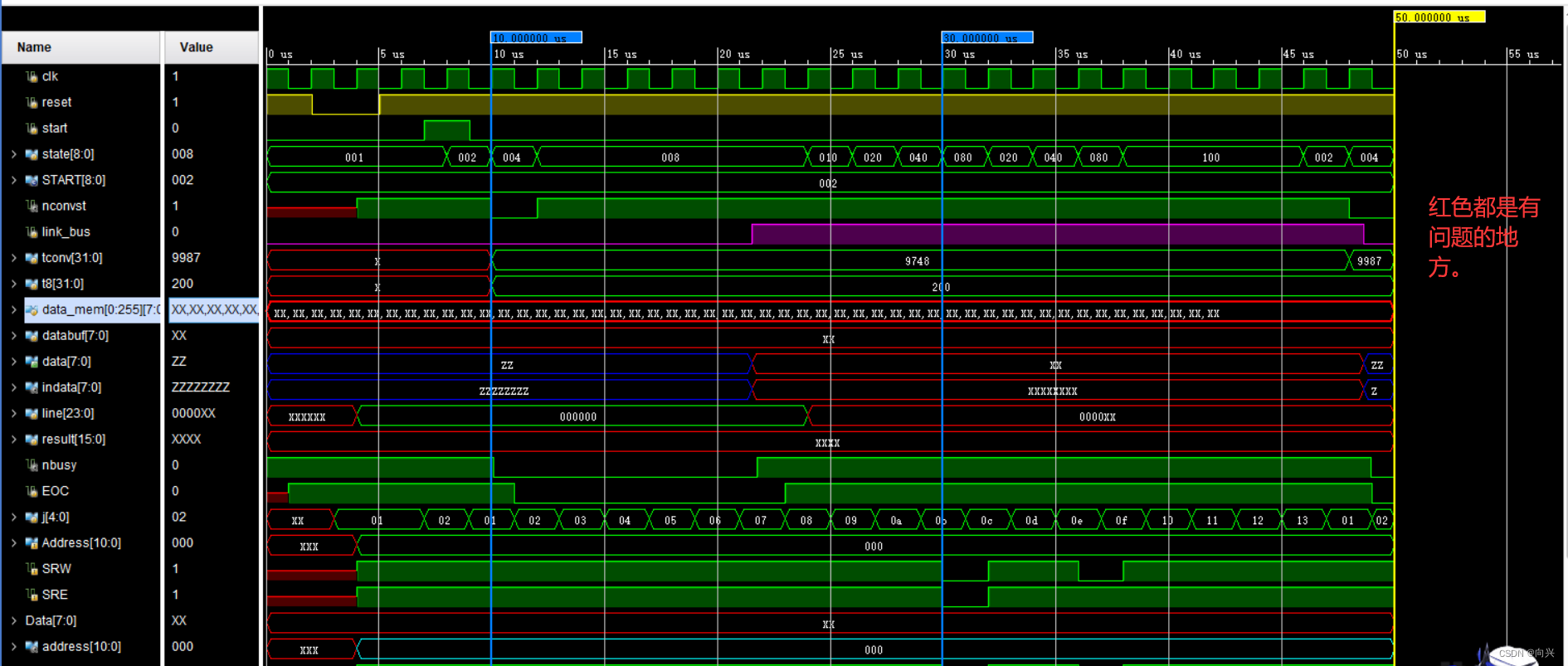
练习十一:简单卷积器的设计
简单卷积器的设计 1,任务目的:2,明确设计任务2.1,目前这部分代码两个文件没找到,见第5、6节,待解决中。 ,卷积器的设计,RTL:con1.v4,前仿真和后仿真,测试信号…...
外包干了4年,技术退步太明显了。。。。。
先说一下自己的情况,本科生生,18年通过校招进入武汉某软件公司,干了接近4年的功能测试,今年国庆,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测…...

微服务实战系列之EhCache
前言 书接前文,继续深耕。上一篇博主对Redis进行了入门级介绍,大体知道了Redis可以干什么以及怎么使用它。 今日博主继续带着大家学习如何使用EhCache,这是一款基于Java的缓存框架。 微服务实战系列之Redis微服务实战系列之Cache微服务实战…...

SpringBoot:SpringMVC(上)
文章目录 前言一、SpringMVC是什么?1.1 MVC的定义:1.2 MVC 和 Spring MVC 的关系 二、Spring MVC 创建和连接2.1创建springmvc2.2接下来,创建⼀个 UserController 类,实现⽤户到 Spring 程序的互联互通,具体实现代码如…...

一文搞懂Go语言中包导入
一文搞懂Go语言中包导入 定义包 在go语言中,定义包的关键字为package,如package main等,在go语言中有一个约定俗成的标准,那就是包名与目录名把持一致。 //service目录下 package servicepackage utils 可以看到,我…...
)
Vue2学习笔记(事件处理)
一、基本使用 1.使用v-on:xxx 或 xxx 绑定事件,其中xxx是事件名;2.事件的回调需要配置在methods对象中,最终会在vm上;3.methods中配置的函数,不要用箭头函数!否则this就不是vm了;4.methods中配…...

【2023第十二届“认证杯”数学中国数学建模国际赛】A题 太阳黑子预报完整解题思路
A题 太阳黑子预报 题目任务思路分析第一问第二问第三问 题目 太阳黑子是太阳光球上的一种现象,表现为比周围区域更暗的临时斑点。它们是由于磁通量集中而导致表面温度降低的区域,磁通量的集中抑制了对流。太阳黑子出现在活跃区域内,通常成对…...
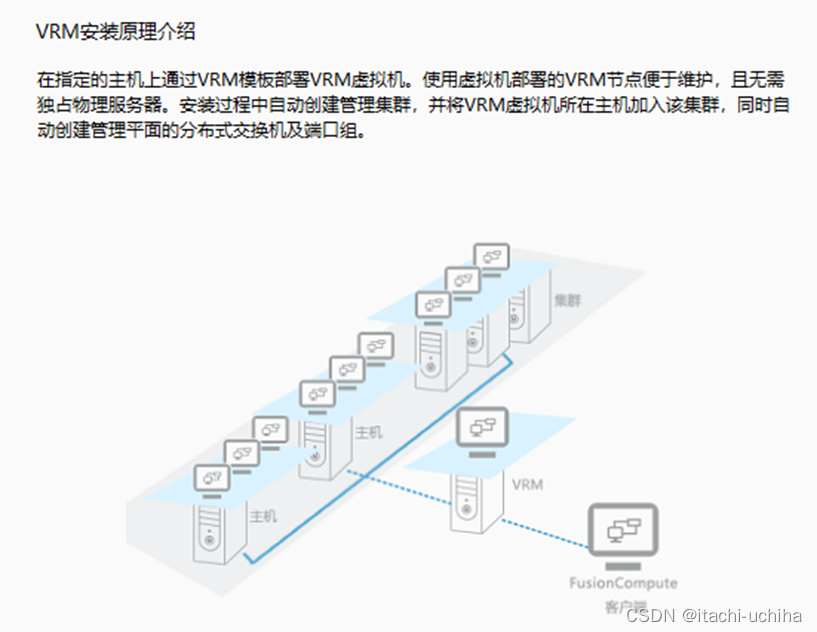
Huawei FusionSphere FusionCompte FusionManager
什么是FusionSphere FusionSphere 解决方案不独立发布软件,由各配套部件发布,请参 《FusionSphere_V100R005C10U1_版本配套表_01》。 目前我们主要讨论FusionManager和FusionCompute两个组件。 什么是FusionCompte FusionCompute是华为提供的虚拟化软…...
GSLB是什么?谈谈对该技术的一点理解
GSLB是什么?它又称为全局负载均衡,是主流的负载均衡类型之一。众所周知,负载均衡位于服务器的前面,负责将客户端请求路由到所有能够满足这些请求的服务器,同时最大限度地提高速度和资源利用率,并确保无任何…...

【接口测试】POST请求提交数据的三种方式及Postman实现
1. 什么是POST请求? POST请求是HTPP协议中一种常用的请求方法,它的使用场景是向客户端向服务器提交数据,比如登录、注册、添加等场景。另一种常用的请求方法是GET,它的使用场景是向服务器获取数据。 2. POST请求提交数据的常见编…...
SpringBoot系列之集成Jedis教程
SpringBoot系列之集成Jedis教程,Jedis是老牌的redis客户端框架,提供了比较齐全的redis使用命令,是一款开源的Java 客户端框架,本文使用Jedis3.1.0加上Springboot2.0,配合spring-boot-starter-data-redis使用࿰…...

centos用什么命令可查看版本号
概述 查版本号的命令:1、“cat /etc/redhat-release”,可输出centos版本号;2、“cat /proc/version”、“uname -a”或“uname -r”,可输出内核版本号。 本教程操作环境:centos7.9.2009系统。 查看centos版本 [roo…...

大数据之Redis
NoSQL SQL数据库泛指关系型数据库NoSQL不拘泥于关系型数据的设计范式,放弃了通用的技术标准,为某一特定领域场景而设计 NoSQL的特点 不遵循SQL标准不支持ACID远超SQL的性能 NoSQL的适用场景 对数据高并发的读写海量数据的读写对数据高可扩展性的 N…...

【React设计】React企业级设计模式
Image Source : https://bugfender.com React是一个强大的JavaScript库,用于构建用户界面。其基于组件的体系结构和构建可重用组件的能力使其成为许多企业级应用程序的首选。然而,随着应用程序的规模和复杂性的增长,维护和扩展变得更加困难。…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
