动态规划求解 fibonacci 数列
动态规划:
- 动态规划的基本思想是:将原问题拆分为若干子问题,自底向上的求解。
- 是自底向上的求解,即是先计算子问题的解,再得出原问题的解。
思路:
-
创建一个数组,大小为n+1,用于存储斐波那契数列的值。数组的第i个元素对应斐波那契数列的第i项。
-
初始化数组的前两个元素,即F(0) = 0,F(1) = 1。
-
从i=2开始,迭代计算出第i项的值,即F(i) = F(i-1) + F(i-2)。这个值可以直接由数组中的前两个元素得到,所以不需要进行额外的函数调用。
-
循环结束后,数组中的最后一个元素就是斐波那契数列的第n项。
代码:
#include <iostream>
#include <vector>// 定义一个函数,使用动态规划求解斐波那契数列的第n项
int fibonacci_dp(int n) {// 处理基本情况:如果n为0或1,直接返回n,因为F(0)=0,F(1)=1if (n <= 1) {return n;}// 创建一个整型向量fib,大小为n+1,用以存储斐波那契数列的每一项std::vector<int> fib(n + 1);// 初始化斐波那契数列的前两项fib[0] = 0; // 第0项设置为0fib[1] = 1; // 第1项设置为1// 使用循环从第2项开始计算斐波那契数列,直到第n项for (int i = 2; i <= n; ++i) {// 根据斐波那契数列的定义,第i项是前两项之和fib[i] = fib[i - 1] + fib[i - 2];}// 循环结束后,fib[n]中存储的是斐波那契数列的第n项return fib[n];
}// 主函数
int main() {int n;// 提示用户输入要计算的斐波那契数列的项数nstd::cout << "Enter the value of n: ";std::cin >> n; // 读取用户输入的n// 调用fibonacci_dp函数计算第n项的斐波那契数,并将结果存储在result中int result = fibonacci_dp(n);// 输出计算得到的斐波那契数std::cout << "Fibonacci number is: " << result << std::endl;// 主函数返回0,表示程序正常结束return 0;
}
相关文章:

动态规划求解 fibonacci 数列
动态规划: 动态规划的基本思想是:将原问题拆分为若干子问题,自底向上的求解。是自底向上的求解,即是先计算子问题的解,再得出原问题的解。 思路: 创建一个数组,大小为n1,用于存储斐波那契数列的值。数组的…...

js最大公约数的实现有哪些办法
在JavaScript中,有几种常见的方法可以实现最大公约数(GCD)的计算。以下是其中一些方法: 辗转相除法(欧几里德算法): 辗转相除法是一种基于递归的算法,用于计算两个数的最大公约数。它…...
盘后股价狂飙16% — GitLab的DevOps产品在AI时代展现强劲财务业绩
12月4日(周一)在美股收盘后,GitLab的股价狂飙16%!人工智能驱动的DevOps产品继续凸显其平台能力的优势。 GitLab 12 月 4 日股价图 GitLab报告第三季度收入同比增长32%!根据粗略统计,全球已经有接近1万家企…...
unity UI特效遮罩
using System.Collections; using System.Collections.Generic; using UnityEngine;/**UI特效遮罩 1.需要将ScrollRect 的遮罩Mask 换为 2D Mask2.将特效的Render里面的 Masking 设置为*/ public class UIParticleMaskControll : MonoBehaviour {// Start is called before …...

编程模拟支付宝能量产生过程--数据控制流
#模拟支付宝蚂蚁森林的能量产生过程 behavior_points { # 定义行为对应的积分"步行": 2,"生活缴费": 10,"线下支付": 5,"网络购票": 5,"共享单车": 10 }total_points 0 # 初始化总积分while True: # 开…...
SQL Sever 基础知识 - 数据筛选(1)
SQL Sever 基础知识 - 四、数据筛选 四、筛选数据第1节 DISTINCT - 去除重复值1.1 SELECT DISTINCT 子句简介1.2 SELECT DISTINCT 示例1.2.1 DISTINCT 一列示例1.2.2 DISTINCT 多列示例 1.2.3 DISTINCT 具有 null 值示例1.2.4 DISTINCT 与 GROUP BY 对比 第2节 WHERE - 过滤查询…...

2024 Move 中文开发者大会将于1月13–14日在上海举办
*以下文章来源于MoveFuns ,作者MoveFunsDAO 2024 Move 中文开发者大会将于1月13日-1月14日在上海举办。本届 Move 开发者大会以 “Move 生态关键的一年” 为主题。 由 MoveFuns 、OpenBuild 和 MoveBit 主办,Rooch、AptosGlobal、alcove、zkMove 和 Ti…...
基于PHP的在线日语学习平台
有需要请加文章底部Q哦 可远程调试 PHP在线日语学习平台 一 介绍 此日语学习平台基于原生PHP开发,数据库mysql。系统角色分为用户和管理员。(附带参考设计文档) 技术栈:phpmysqlphpstudyvscode 二 功能 学生 1 注册/登录/注销 2 个人中心 3 查看课程…...
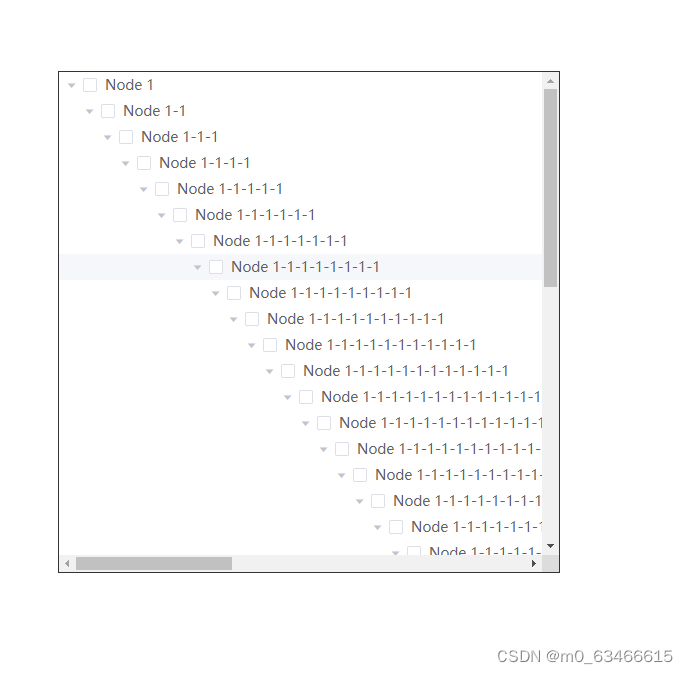
解决element ui tree组件不产生横向滚动条
结果是这样的 需要在tree的外层,包一个父组件 <div class"tree"><el-tree :data"treeData" show-checkbox default-expand-all></el-tree></div> 在css里面这样写,样式穿透按自己使用的css编译器以及框架要求就好 &l…...
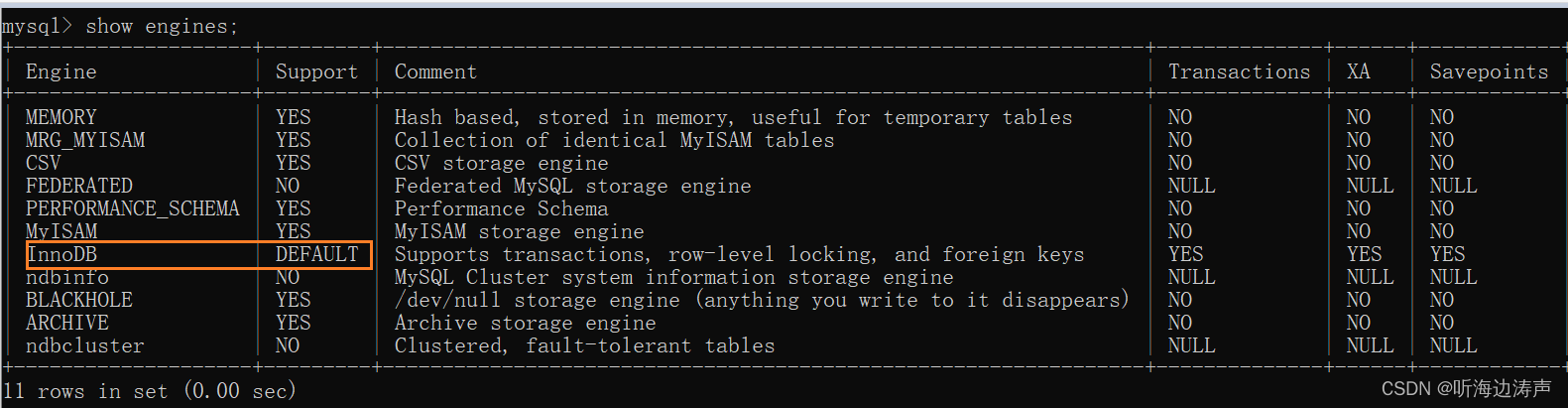
mysql的InnoDB存储引擎
详情请参考:https://dev.mysql.com/doc/refman/8.0/en/innodb-storage-engine.html InnoDB 是一个通用目的的存储引擎,它在高可用性、高性能方面做了平衡。MySQL 8.0,InnoDB 是默认的存储引擎。在创建表的时候,如果没有使用ENGIN…...

MCU 的 TOP 15 图形GUI库:选择最适合你的图形用户界面(二)
在嵌入式系统开发中,选择一个合适的图形用户界面(GUI)库是至关重要的。在屏幕上显示的时候,使用现成的图形库,这样开发人员就不需要弄清楚底层任务,例如如何绘制像素、线条、形状,如果再高级一点…...

软件工程 单选多选补充 复刻
原文 软件的主要特性:无形、高成本、包括程序和文档 软件工程三要素:方法、工具、过程 螺旋模型包含风险分析 软件工程的主要目标:风险分析 面向对象开发:Booch、UML、Coad、OMT 软件危机的主要表现:软件成本太高…...

微前端个人理解与简单总结
最近一段时间在学习微前端,一开始是看各种博客了解微前端含义、对比多种微前端框架优劣,最后选择了qiankun、micro-app、wujie这三种微前端框架进行深入研究、对比。 微前端框架 推出时间 官方文档易读性 社区讨论活跃度 配置难度 Qiankunÿ…...

PC端企业微信hook协议开发,获取要群发的客户群id
产品说明 一、 hook版本:企业微信hook接口是指将企业微信的功能封装成dll,并提供简易的接口给程序调用。通过hook技术,可以在不修改企业微信客户端源代码的情况下,实现对企业微信客户端的功能进行扩展和定制化。企业微信hook接口…...
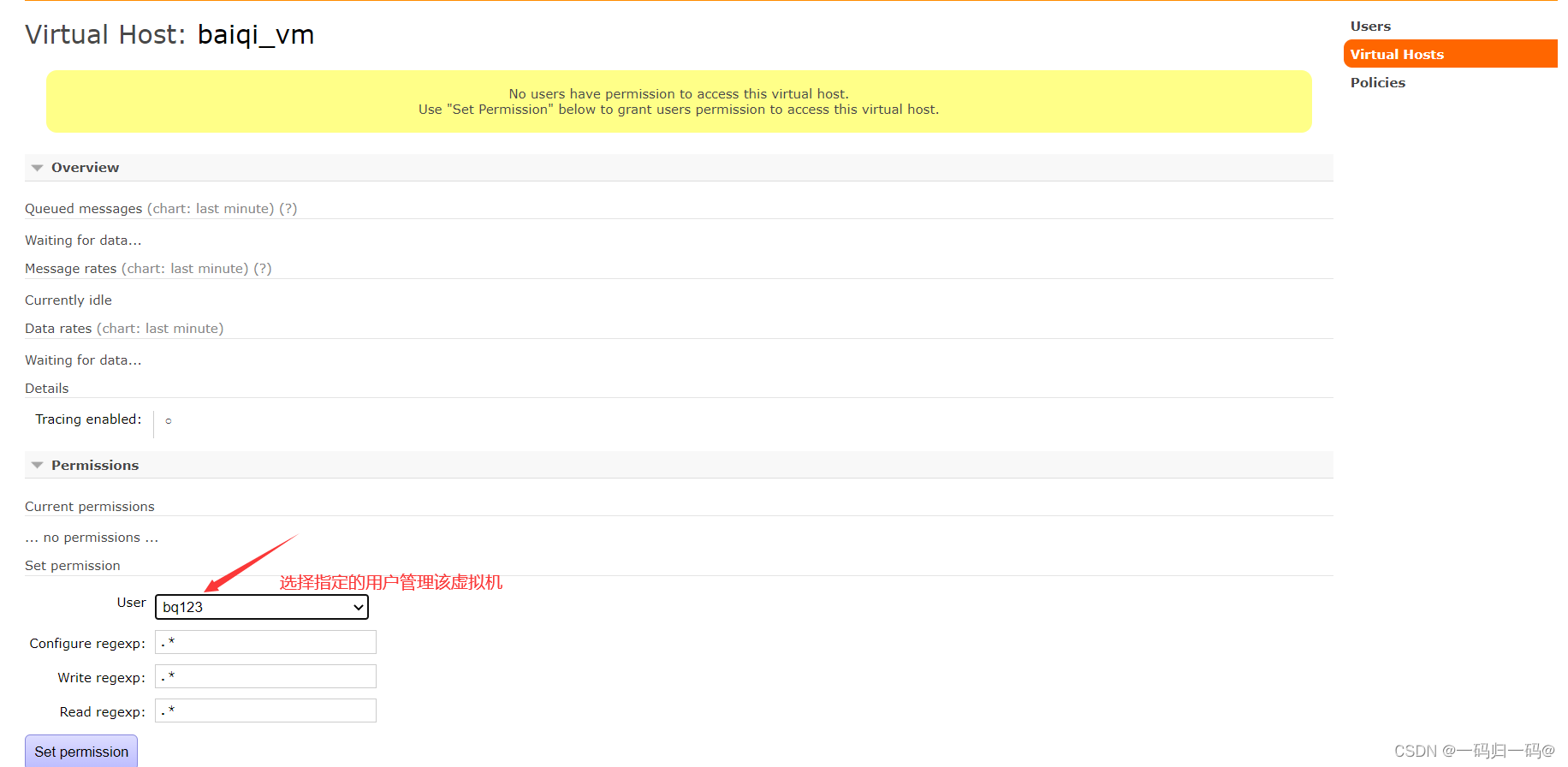
RabbitMQ安装说明
注意: 本次安装以 CentOS 7为例 1、 准备软件 erlang 18.3 1.el7.centos.x86_64.rpm socat 1.7.3.2 5.el7.lux.x86_64.rpm rabbitmq server 3.6.5 1.noarch.rpm 2、安装Erlang rpm -ivh erlang-18.3-1.el7.centos.x86_64.rpm 3.、安装RabbitMQ 安装 rpm -ivh socat-1.7.3.2-…...

scrapy的建模及管道的使用
一、数据建模 通常在做项目的过程中,在items.py中进行数据建模 为什么建模 定义item即提前规划好哪些字段需要抓,防止手误,因为定义好之后,在运行过程中,系统会自动检查,配合注释一起可以清晰的知道要抓…...
-Part.04 基础环境配置)
Hadoop学习笔记(HDP)-Part.04 基础环境配置
目录 Part.01 关于HDP Part.02 核心组件原理 Part.03 资源规划 Part.04 基础环境配置 Part.05 Yum源配置 Part.06 安装OracleJDK Part.07 安装MySQL Part.08 部署Ambari集群 Part.09 安装OpenLDAP Part.10 创建集群 Part.11 安装Kerberos Part.12 安装HDFS Part.13 安装Ranger …...

【Linux】进程控制--进程创建/进程终止/进程等待/进程程序替换/简易shell实现
文章目录 一、进程创建1.fork函数2.fork函数返回值3.写时拷贝4.fork常规用法5.fork调用失败的原因 二、进程终止1.进程退出码2.进程退出场景3.进程常见退出方法 三、进程等待1.为什么要进行进程等待2.如何进行进程等待1.wait方法2.waitpid方法3.获取子进程status4.进程的阻塞等…...

用pip更新、安装python的包
查看pip的版本:python -m pip --version 例如,查看下pip的版本,在cmd下输入命令python -m pip --version,可以发现当前安装的pip的版本是23.2.1: 查看一个包的详情:python -m pip show 例如,…...

spring boot 事件机制
目录 概述实践监听spring boot ready事件代码 源码初始化流程调用流程 结束 概述 spring boot 版本为 2.7.17 。 整体看一下spring及spring boot 相关事件。 根据下文所给的源码关键处,打上断点,可以进行快速调试。降低源码阅读难度。 实践 spring…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
