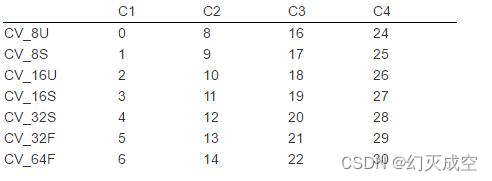
使用opencv将sRGB格式的图片转换为BT.2020格式【sRGB】【BT.2020】
将sRGB格式的图片转换为BT.2020格式涉及到两个步骤:首先将sRGB转换到线性RGB,然后将线性RGB转换到BT.2020。这是因为sRGB图像通常使用伽马校正,而BT.2020工作在线性色彩空间中。
-
从sRGB到线性RGB:sRGB图像首先需要进行伽马校正解码转换为线性RGB。这个过程通常不是通过一个简单的线性矩阵实现的,而是通过以下公式:
[
C_{linear} = \begin{cases}
\frac{C_{sRGB}}{12.92}, & \text{if } C_{sRGB} \leq 0.04045 \
\left(\frac{C_{sRGB} + 0.055}{1.055}\right)^{2.4}, & \text{otherwise}
\end{cases}
]其中 (C_{linear}) 是线性RGB中的颜色分量值(红、绿、蓝),(C_{sRGB}) 是sRGB颜色空间中的对应分量值。
-
从线性RGB到BT.2020:接下来,您可以应用一个3x3的线性转换矩阵将线性RGB转换为BT.2020色彩空间。这个矩阵通常如下所示:
[
\begin{bmatrix}
R_{BT.2020} \
G_{BT.2020} \
B_{BT.2020}
\end{bmatrix}\begin{bmatrix}
0.6274 & 0.3293 & 0.0433 \
0.0691 & 0.9195 & 0.0114 \
0.0164 & 0.0880 & 0.8956
\end{bmatrix}
\cdot
\begin{bmatrix}
R_{linear} \
G_{linear} \
B_{linear}
\end{bmatrix}
]
在实际应用中,你首先需要编写代码将sRGB图像转换为线性RGB,然后再应用上述矩阵进行色彩空间的转换。以下是使用OpenCV在C++中实现这一过程的示例代码:
#include <opencv2/opencv.hpp>
#include <cmath>cv::Mat sRGBToLinearRGB(const cv::Mat& srgbImage) {cv::Mat linearRGB(srgbImage.size(), srgbImage.type());// cv::Vec3b,static_cast<uchar> 这2个要根据图片格式选择合适的值srgbImage.forEach<cv::Vec3b>([&](cv::Vec3b &pixel, const int * position) -> void {for (int i = 0; i < 3; ++i) {float c = pixel[i] / 255.0f;c = c <= 0.04045f ? c / 12.92f : std::pow((c + 0.055f) / 1.055f, 2.4f);linearRGB.at<cv::Vec3b>(position)[i] = static_cast<uchar>(std::round(c * 255.0f));}});return linearRGB;
}int main() {// 假设你已经有了一个sRGB格式的cv::Mat对象 srgbImagecv::Mat srgbImage; // 加载你的sRGB图像// 将sRGB转换为线性RGBcv::Mat linearRGB = sRGBToLinearRGB(srgbImage);// 定义从线性RGB到BT.2020的转换矩阵cv::Matx33f transformMatrix(0.6274, 0.3293, 0.0433,0.0691, 0.9195, 0.0114,0.0164, 0.0880, 0.8956);// 应用转换矩阵cv::Mat bt2020Image;cv::transform(linearRGB, bt2020Image, transformMatrix);// bt2020Image现在包含转换后的图像return 0;
}
cv::Mat sRGBToLinearRGB(const cv::Mat& srgbImage) {cv::Mat linearRGB(srgbImage.size(), srgbImage.type());srgbImage.forEach<cv::Vec3f>([&](cv::Vec3f &pixel, const int * position) -> void {for (int i = 0; i < 3; ++i) {float c = pixel[i] / 255.0f;auto c2 = (c <= 0.04045f) ? (c / 12.92f) : std::pow((c + 0.055f) / 1.055f, 2.4f);auto val = static_cast<float>(std::round(c2 * 255.0f));qDebug() << QString("pixel[i] = %1, c1 = %2, c2 = %3, val = %4").arg(pixel[i]).arg(c).arg(c2).arg(val);linearRGB.at<cv::Vec3f>(position)[i] = val;}});return linearRGB;}cv::Mat Image_sRGB_BT2020(const cv::Mat &src){cv::Mat dst = src;// 确保使用浮点数src.convertTo(dst, CV_32F);// 将sRGB转换为线性RGBcv::Mat linearRGB = sRGBToLinearRGB(dst);// 定义从线性RGB到BT.2020的转换矩阵cv::Matx33f transformMatrix(0.6274, 0.3293, 0.0433,0.0691, 0.9195, 0.0114,0.0164, 0.0880, 0.8956);// 应用转换矩阵cv::Mat bt2020Image;cv::transform(linearRGB, bt2020Image, transformMatrix);return bt2020Image;}
相关文章:

使用opencv将sRGB格式的图片转换为BT.2020格式【sRGB】【BT.2020】
将sRGB格式的图片转换为BT.2020格式涉及到两个步骤:首先将sRGB转换到线性RGB,然后将线性RGB转换到BT.2020。这是因为sRGB图像通常使用伽马校正,而BT.2020工作在线性色彩空间中。 从sRGB到线性RGB:sRGB图像首先需要进行伽马校正解码…...

聊天注意事项
聊天成功的核心就是双方都能舒服 有些人不会聊天是缺乏引导性 聊天聊两句话就没了 聊天要把话题引导向对方 从倾诉者变为倾听者 才能不断交流 沟通不是一个人的独角戏 每个人都渴望被理解 要注意倾听别人说的话 不要只顾自己说一大堆,别人都瞌睡了 不要查户口式问…...
12.5 作业
1, 以下是一个简单的比喻,将多态概念与生活中的实际情况相联系: 比喻:动物园的讲解员和动物表演 想象一下你去了一家动物园,看到了许多不同种类的动物,如狮子、大象、猴子等。现在,动物园里有…...

深入理解指针3
hello,各位小伙伴,本篇文章跟大家一起继续深入学习指针,感谢大家对我上一篇的支持,如有什么问题,还请多多指教 如果本篇文章对你有帮助,还请各位点点赞!!! 话不多说&am…...

大数据环境下在线考试系统安全策略研究
摘 要 随着云计算、物联网、电子商务、企业信息化等的飞速发展,以及智能终端和各种检测、感应设备的普及和建设,全球逐渐进入信息化、网络化,由此产生了指数爆炸般的数据增长,一个大规模生产、分享和应用的数据的时代正在开启&am…...
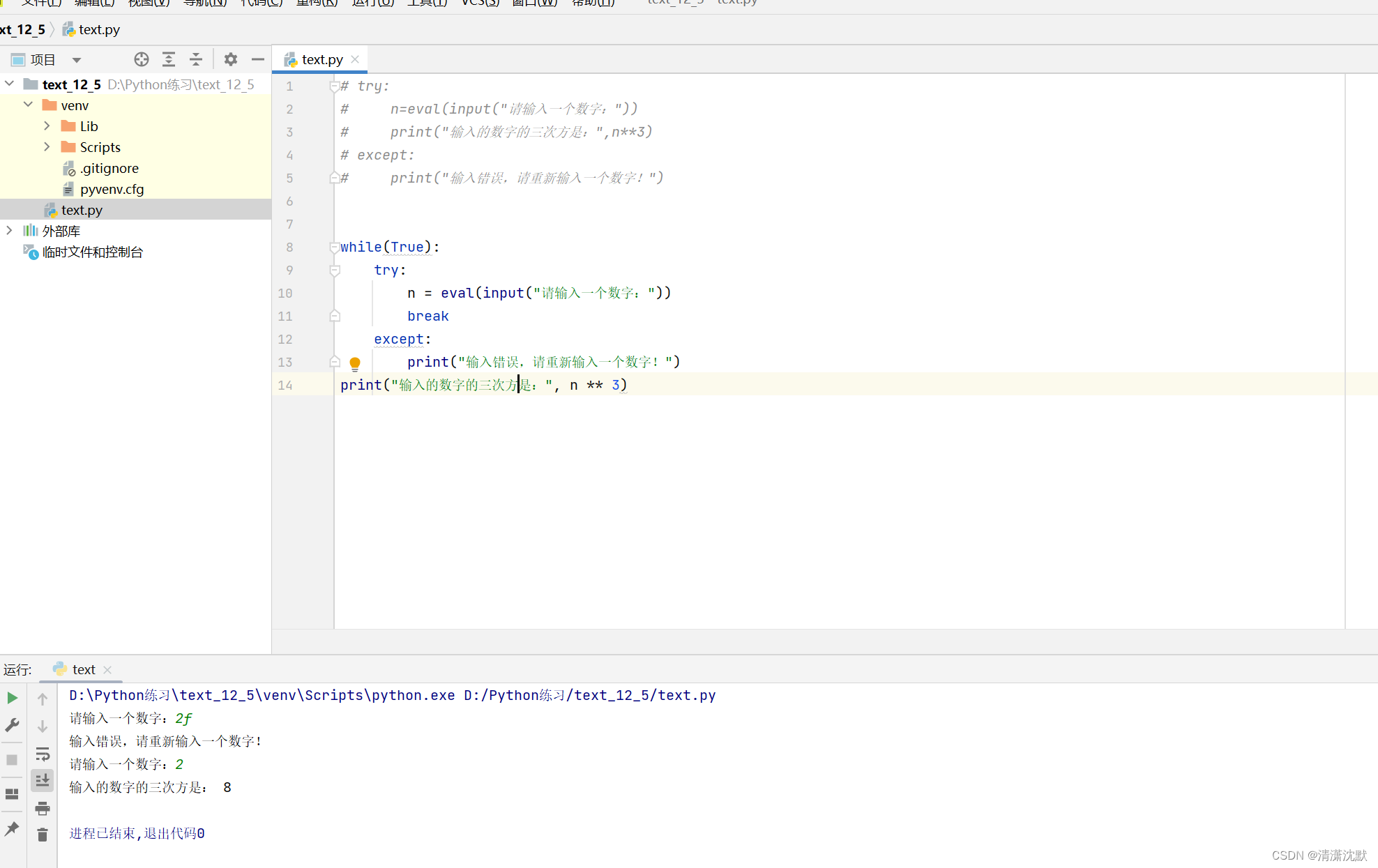
Python中程序的异常处理
Python程序一般对输入有一定要求,担当实际输入不满足程序要求时,可能会产生程序的运行错误。Python语言使用的保留太容易try和except进行异常处理! try: 语句块1 except: 语句块2 语句块1是正常执行的程序内容,当这个语句块发生异…...
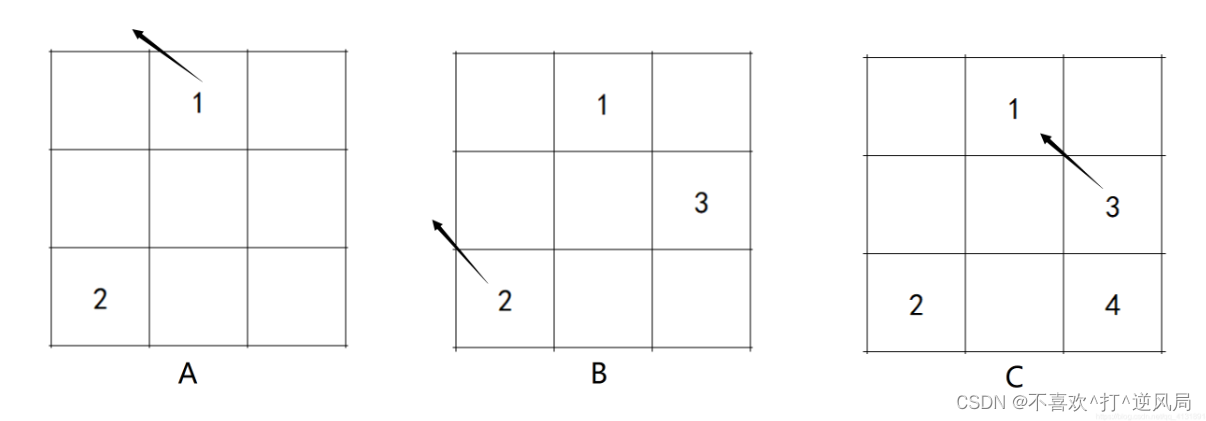
有趣的代码——有故事背景的程序设计3
这篇文章再和大家分享一些有“背景”的程序设计,希望能够让大家学到知识的同时,对编程学习更感兴趣,更能在这条路上坚定地走下去。 目录 1.幻方问题 2.用函数打印九九乘法表 3.鸡兔同笼问题 4.字数统计 5.简单选择排序 1.幻方问题 幻方又…...

聚观早报 |国行PS5轻薄版开售;岚图汽车11月交付7006辆
【聚观365】12月2日消息 国行PS5轻薄版开售 岚图汽车11月交付7006辆 比亚迪推出12月限时优惠 特斯拉正式交付首批Cybertruck 昆仑万维发布「天工 SkyAgents」平台 国行PS5轻薄版开售 索尼最新的PlayStation5主机(CFI-2000型号组-轻薄版)国行版本正…...
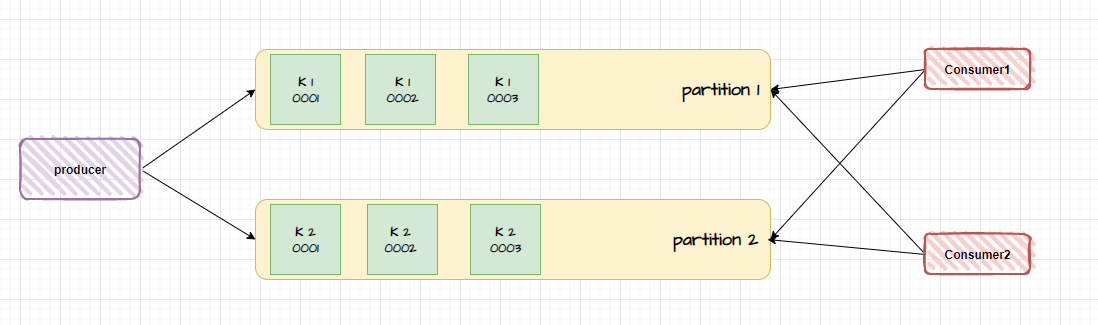
Kafka 保证消息消费全局顺序性
当有消息被生产出来的时候,如果没有指定分区或者指定 key ,那么消费会按照【轮询】的方式均匀地分配到所有可用分区中,但不一定按照分区顺序来分配 我们知道,在 Kafka 中消费者可以订阅一个或多个主题,并被分配一个或多…...

3分钟在CentOS 7上离线安装Docker
在CentOS 7上离线安装Docker的详细步骤如下: 环境检查和准备 检查内核版本:Docker要求系统为64位且内核版本至少为3.10。使用命令uname -r查看内核版本。 检查CentOS版本:通过命令cat /etc/redhat-release查看版本信息。 更新yum包࿰…...
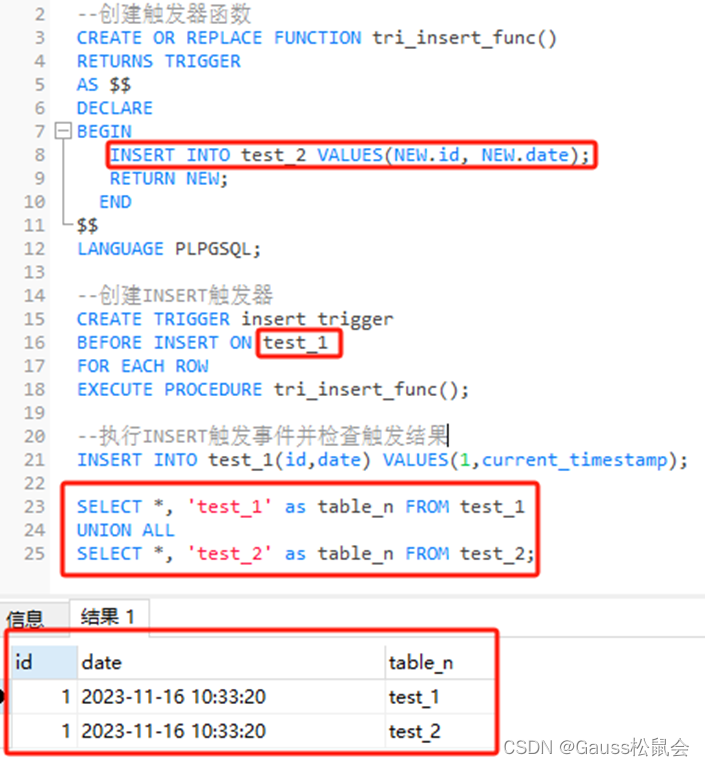
GaussDB数据库SQL系列-触发器
目录 一、前言 二、触发器概念 三、GaussDB数据库中的触发器 1、语法格式 2、创建步骤 3、注意事项 4、附:表和视图上支持的触发器种类 四、GaussDB数据库中的示例 示例一、在GaussDB数据库中创建一个触发器,以便在插入新记录时自动将记录的创建…...
网工学习10-IP地址
一、IP地址概念 IP地址是一个32位的二进制数,它由网络ID和主机ID两部份组成,用来在网络中唯一的标识的一台计算机。网络ID用来标识计算机所处的网段;主机ID用来标识计算机在网段中的位置。IP地址通常用4组3位十进制数表示,中间用…...
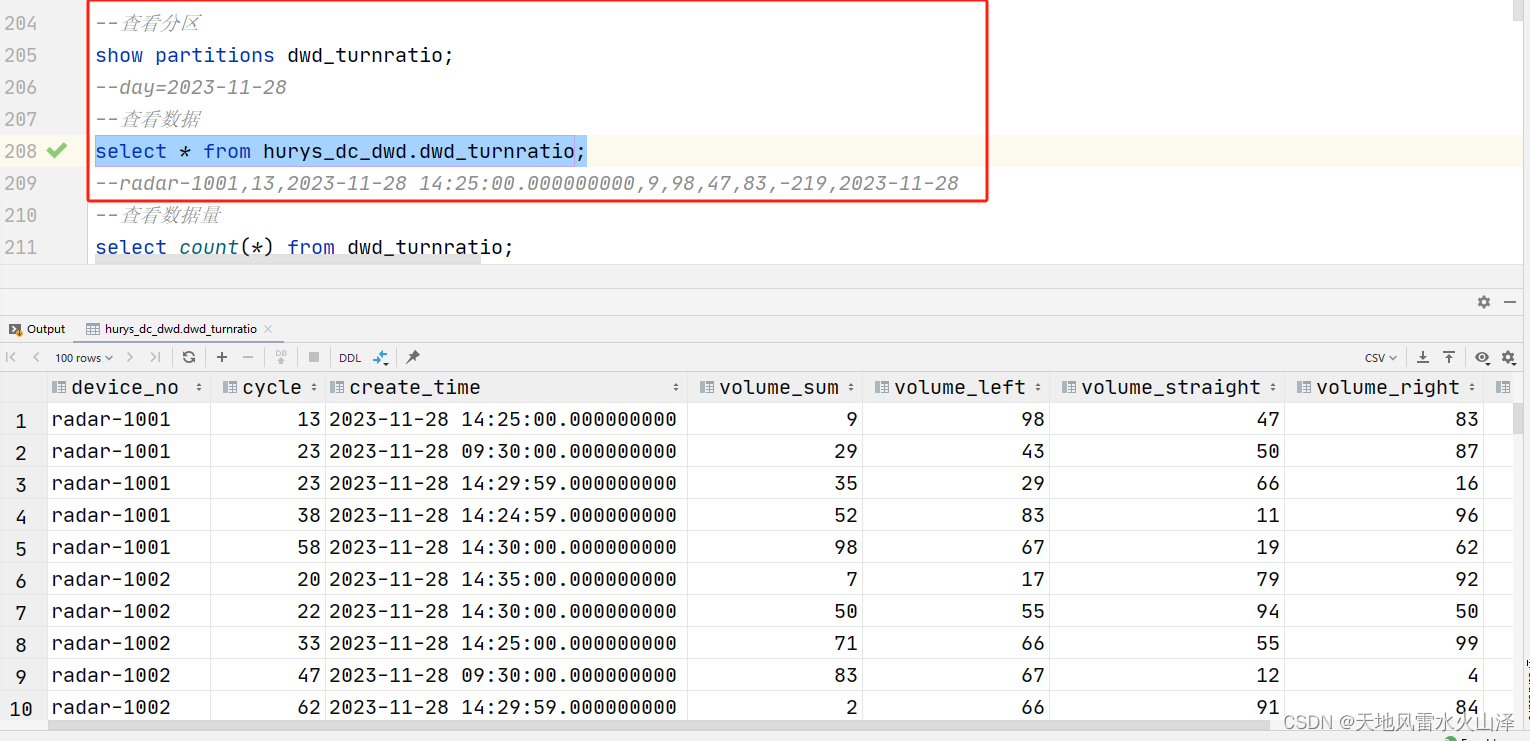
二百零八、Hive——HiveSQL异常:Select查询数据正常,但SQL语句加上group by查询数据为空
一、目的 在HiveSQL的DWD层中,需要对原始数据进行去重在内的清洗,结果一开始其他数据类型的清洗工作都正常,直到碰到转向比数据。 一般的SQL查询有数据,但是加上group by以后就没数据; 一般的SQL查询有数据…...
Docker—共享应用程序
现在您已经构建了一个映像,可以共享它。要共享Docker映像,您必须使用Docker注册表。默认注册表是Docker Hub,是您使用的所有图像的来源。 Docker ID(Docker标识) Docker ID允许您访问Docker Hub,这是世界上…...

Linux横向移动
Linux横向移动 主机存活探测 shell for i in 192.168.111.{1..254}; do if ping -c 3 -w 3 $i &>/dev/null; then echo $i is alived; fi; done 或者 for k in $( seq 1 255);do ping -c 1 192.168.1.$k|grep "ttl"|awk -F "[ :]" {print $4}; d…...
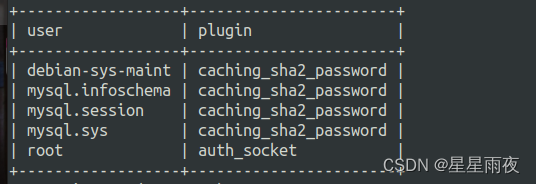
Ubuntu 20.0 + mysql 8.0 用户和密码修改
第一步 下载(简单,注意联网)Ubuntu 终端输入以下两行命令 (1) 数据库的服务端及客户端数据库的开发软件包 sudo apt-get install mysql-server mysql-client (2) 数据库的开发软件包 sudo apt-get install libmysqlclient-dev 第二步 查看是否安装成功 …...

看懂lscpu的输出
文章目录 1. lscpu1.1 Architecture1.2 逻辑核心数1.3 缓存1.4 CPU型号1.5 NUMA架构1.5.1 CPU多核架构1.5.2 多CPU Socket架构 2. cat /proc/cpuinfo2.1 关键字段 1. lscpu 通过lscpu查看当前系统的CPU信息。 [hadoopserver3 ~]$ lscpuArchitecture: x86_64 …...
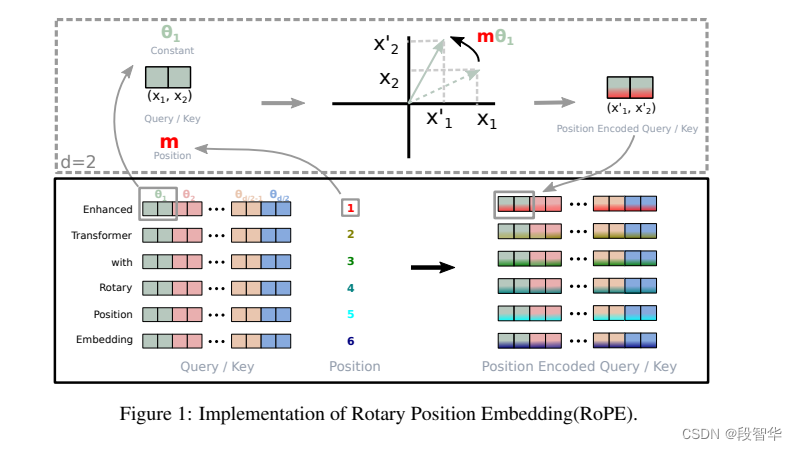
RoPE旋转位置编码浅析
RoPE旋转位置编码浅析 本文介绍了旋转位置编码RoPE在大模型中的广泛应用,包括Llama、Mistral 7B、Baichuan、ChatGLM、Qwen、…等。由于计算资源限制,大模型通常在较小的上下文长度中进行训练,导致在推理超出预训练长度时性能显著下降。为了解决这个问题,涌现了许多基于Ro…...
在 SQL Server 中备份和恢复数据库的最佳方法
在SQL Server中,创建备份和执行还原操作对于确保数据完整性、灾难恢复和数据库维护至关重要。以下是备份和恢复过程的概述: 方法 1. 使用 SQL Server Management Studio (SSMS) 备份和还原数据库 按照 SSMS 步骤备份 SQL 数据库 打开 SSMS 并连接到您…...

Java8 根据自定义属性去重
一、需求背景 有一个List集合,里面有n个Answer成员,成员种有m个属性,即: List<Answer> answers ...,现在我需要根据Answer的某一个属性对List去重(属性不固定),应该如何实现呢? 二、解决办法 需要满足上述需求,并不难,我们可以使用Java8提供的…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
