二叉树链式结构的实现和二叉树的遍历以及判断完全二叉树
二叉树的实现
定义结构体
我们首先定义一个结构来存放二叉树的节点
结构体里分别存放左子节点和右子节点以及节点存放的数据
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
构造一个二叉树
我们首先定义一个新建新节点的函数,方便构造二叉树
BTNode* buynode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;
}
然后就是构造二叉树之间的节点关系和节点中存储的元素
这里我们构造的是一个满二叉树,各个节点关系如下图所示
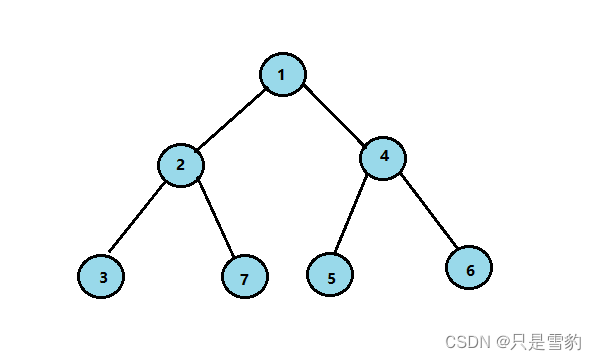
BTNode* createtree()
{BTNode* node1 = buynode(1);BTNode* node2 = buynode(2);BTNode* node3 = buynode(3);BTNode* node4 = buynode(4);BTNode* node5 = buynode(5);BTNode* node6 = buynode(6);BTNode* node7 = buynode(7);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;node2->right= node7;//满二叉树return node1;
}
返回二叉树节点个数
这里有两种方法:
一种是遇到空节点直接返回,否则size++,然后再递归使用左节点和右节点,这种方法就做计数
第二种是直接递归使用左节点加右节点+1,这种方法更加简洁,但是可读性没有第一种方法这么好
int BinaryTreeSize(BTNode* root)
{//static size = 0;//if (root == NULL)// return;//size++;//BinaryTreeSize(root->left);//BinaryTreeSize(root->right);//return size;if (root == NULL)return 0;return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
返回二叉树叶子节点个数
叶子节点就是没有孩子,即左节点和右节点都为空
当根节点root为空时直接返回0,当左节点left和右节点right都为空是就返回1,然后递归root的左节点和右节点相加,最后返回的就是叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
返回二叉树第k层节点个数
这里的二叉树根节点是第一层
首先k必须大于0,进行断言
如果根节点为空就直接返回0
如果k为1,就只有根节点一个节点,返回1
再递归左子树的k-1和右子树的k-1层节点数相加就是第k层的节点数
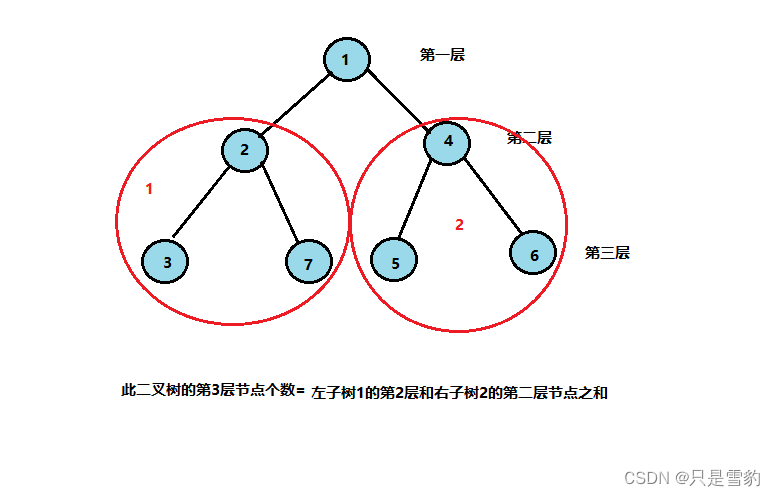
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
二叉树查找值为x的节点
查找节点其实大家都有误区
例如:
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;
BinaryTreeFind(root->left, x);BinaryTreeFind(root->right, x);
}
但是这种情况下如果没有这个节点怎么办呢
所以这是错误滴
正确的在下面:
我们申请空间分别存放递归后左节点和右节点的返回值,如果不为空就返回
如果到最后还没有返回值就是二叉树中没有这个节点,直接返回空
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* node1 = BinaryTreeFind(root->left, x);if (node1)return node1;BTNode* node2 = BinaryTreeFind(root->right, x);if (node2)return node2;return NULL;
}
二叉树的销毁
很简单,但是记得手动置空
void BinaryTreeDestory(BTNode* root)
{if (root == NULL)return;BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);//为了防止出现野指针,需要使用者自己手动置空,即root==Null
}
求二叉树的高度
其实而二叉树的高度就是层数,我们只要计算层数最多的分支即可
如果左子树大于右子树就返回左子树的递归结果+1,右子树反之
大家看一下下面这段代码
int BinaryTreeHeight(BTNode* root)
{if (root == NULL)return 0;return BinaryTreeHeight(root->left) > BinaryTreeHeight(root->right) ? BinaryTreeHeight(root->left) + 1 : BinaryTreeHeight(root->right) + 1;
}
上面这段代码是有问题的,他没有将其记录下来,就回返回很多次去查询数据,导致超出时间限制
下面这段代码给出了解决的办法
记录即可
int BinaryTreeHeight(BTNode* root)
{if (root == NULL)return 0;int leftheight = BinaryTreeHeight(root->left);int rightheight = BinaryTreeHeight(root->right);return leftheight > rightheight ? leftheight + 1 : rightheight+1;
}
二叉树的遍历
前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
前序、中序以及后序遍历的实现
这三个遍历很简单,难得是层序遍历
前序就是先访问根节点,然后左子树右子树,用递归解决即可
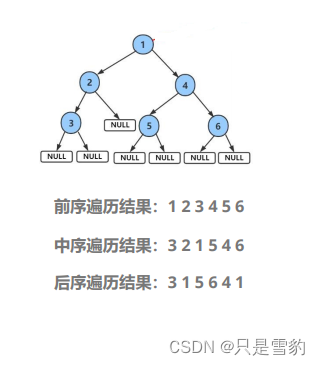
前序
void BinaryTreePrevOrder(BTNode* root)
{if (root){ putchar(root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);}
}
中序
void BinaryTreeInOrder(BTNode* root)
{if (root){BinaryTreeInOrder(root->_left);putchar(root->_data);BinaryTreeInOrder(root->_right);}
}
后序
void BinaryTreePostOrder(BTNode* root)
{if (root){BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);putchar(root->_data);}
}
层序遍历的实现
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
看图理解即可:
访问顺序是
A B C D E F G
层序遍历得实现其实要用到队列:
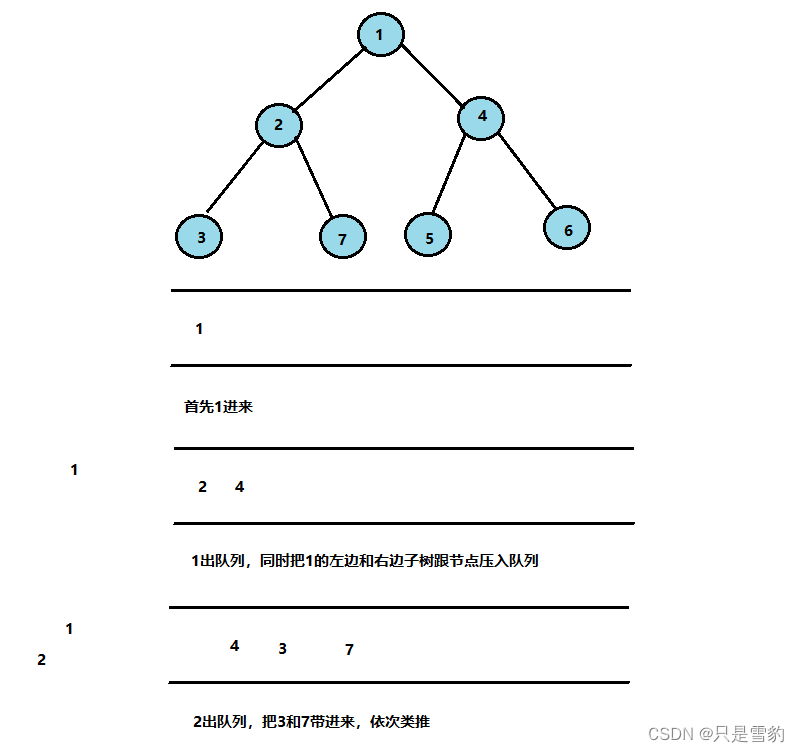
上图给了一个解释,大家可以研究研究
void BinaryTreeLevelOrder(BTNode* root)
{Queue qu;BTNode * cur;QueueInit(&qu);//首先压入根节点QueuePush(&qu, root);//循环的终止条件就是当队列为空时,此时二叉树层序遍历完成while (!QueueIsEmpty(&qu)){//第一次进入循环时cur为队列的队首,即根节点cur = QueueTop(&qu);putchar(cur->data);//当cur的左不为空是入队列if (cur->left){QueuePush(&qu, cur->left);}//当cur的右不为空是入队列if (cur->right){QueuePush(&qu, cur->right);}//删除此时的队首元素,并返回打印QueuePop(&qu);}QueueDestory(&qu);
}
二叉树是否为完全二叉树
判断是否未完全二叉树的条件是什么呢
就是层序遍历完成时中间有无空节点!
我们首先将根节点压入队列
然后再将队列队首元素删除返回后,判断队首元素是否为空,为空则跳出while循环,就当他是个完全二叉树的所有节点已经全部压入
如果不是空就将左子树和右子树的根节点压入
然后我们再用层序遍历来判断后面是否有非空节点,如果有的话就不是完全二叉树,return false
否则是完全二叉树
看图分析即可:
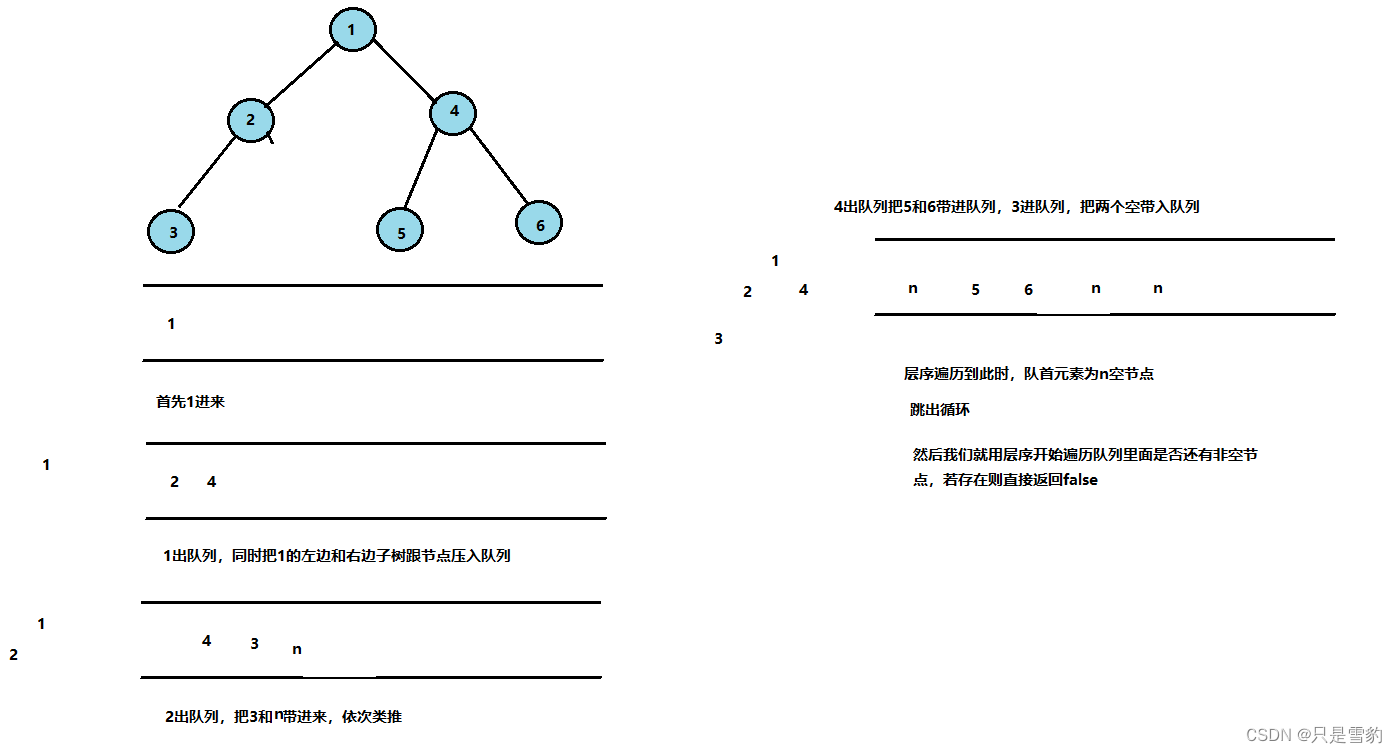
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)//遇空就跳出break;QueuePush(&q, front->left);QueuePush(&q, front->right);}
//检查后面是否有非空节点,有非空就是非完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}
好了,本文到此结束,感谢大家的支持!
相关文章:

二叉树链式结构的实现和二叉树的遍历以及判断完全二叉树
二叉树的实现 定义结构体 我们首先定义一个结构来存放二叉树的节点 结构体里分别存放左子节点和右子节点以及节点存放的数据 typedef int BTDataType; typedef struct BinaryTreeNode {BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right; }BTNode;…...

vue中的动画组件使用及如何在vue中使用animate.css
“< Transition >” 是一个内置组件,这意味着它在任意别的组件中都可以被使用,无需注册。它可以将进入和离开动画应用到通过默认插槽传递给它的元素或组件上。进入或离开可以由以下的条件之一触发: 由 v-if 所触发的切换由 v-show 所触…...

qt 5.15.2 网络文件下载功能
qt 5.15.2 网络文件下载功能 #include <QCoreApplication>#include <iostream> #include <QFile> #include <QTextStream> // #include <QtCore> #include <QtNetwork> #include <QNetworkAccessManager> #include <QNetworkRep…...

Wifi adb 操作步骤
1.连接usb 到主机 手机开起热点,电脑和车机连接手机,或者电脑开热点,车机连接电脑,车机和电脑连接同一个网络 因为需要先使用usb,后面切换到wifi usb 2.查看车机ip地址,和电脑ip地址 电脑win键r 输入cmd…...

湿货 - 231206 - 关于如何构造输入输出数据并读写至文件中
TAG - 造数据、读写文件 造数据、读写文件 造数据、读写文件//*.in // #include<bits/stdc.h> using namespace std;/* *********** *********** 全局 ********** *********** */ string Pre_File_Name; ofstream IN_cout; int idx;void Modify_ABS_Path( string& …...
EasyMicrobiome-易扩增子、易宏基因组等分析流程依赖常用软件、脚本文件和数据库注释文件
啥也不说了,这个好用,给大家推荐:YongxinLiu/EasyMicrobiome (github.com) 大家先看看引用文献吧,很有用:https://doi.org/10.1002/imt2.83 还有这个,后面马上介绍:YongxinLiu/EasyAmplicon: E…...

【Python百宝箱】漫游Python数据可视化宇宙:pyspark、dash、streamlit、matplotlib、seaborn全景式导览
Python数据可视化大比拼:从大数据处理到交互式Web应用 前言 在当今数字时代,数据可视化是解释和传达信息的不可或缺的工具之一。本文将深入探讨Python中流行的数据可视化库,从大数据处理到交互式Web应用,为读者提供全面的了解和…...

企业数字档案馆室建设指南
数字化时代,企业数字化转型已经成为当下各行业发展的必然趋势。企业数字化转型不仅仅是IT系统的升级,也包括企业内部各种文件、档案、合同等信息的数字化管理。因此,建设数字档案馆室也变得尤为重要。本篇文章将为您介绍企业数字档案馆室建设…...

JavaScript中处理时间差
ES6版本 function countdown(endTime, includeSeconds true) {// 获取当前时间let now new Date();// 将传入的结束时间字符串转换为日期对象let endDateTime new Date(endTime);// 检查传入的时间字符串是否只包含日期(不包含时分秒)if (endTime.tr…...
Multidimensional Scaling(MDS多维缩放)算法及其应用
在这篇博客中,我将与大家分享在流形分析领域的一个非常重要的方法,即多维缩放MDS。整体来说,该方法提供了一种将内蕴距离映射到显性欧氏空间的计算,为非刚性形状分析提供了一种解决方案。当初就是因为读了Bronstein的相关工作【1】…...

单片机_RTOS_架构
一. RTOS的概念 // 经典单片机程序 void main() {while (1){喂一口饭();回一个信息();} } ------------------------------------------------------ // RTOS程序 喂饭() {while (1){喂一口饭();} }回信息() {while (1){回一个信息();} }void main() {create_task(喂饭);cr…...

Golang rsa 验证
一下代码用于rsa 签名的验签, 签名可以用其他语言产生。也可以用golang生成。 package mainimport ("crypto""crypto/rsa""crypto/sha256""crypto/x509""encoding/pem""errors""fmt" )fun…...

网络安全威胁——跨站脚本攻击
跨站脚本攻击 1. 定义2. 跨站脚本攻击如何工作3. 跨站脚本攻击类型4. 如何防止跨站脚本攻击 1. 定义 跨站脚本攻击(Cross-site Scripting,通常称为XSS),是一种典型的Web程序漏洞利用攻击,在线论坛、博客、留言板等共享…...
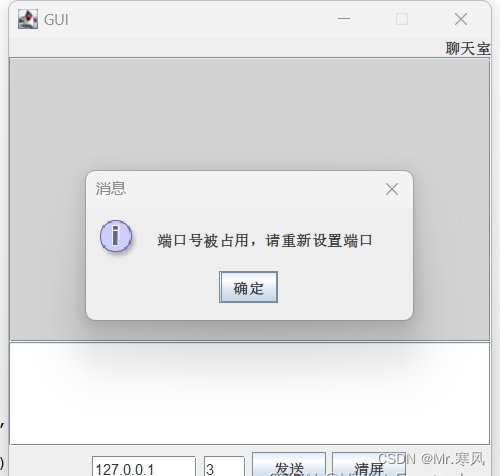
Java利用UDP实现简单的双人聊天
一、创建新项目 首先创建一个新的项目,并命名。 二、实现代码 import java.awt.*; import java.awt.event.*; import javax.swing.*; import java.net.*; import java.io.IOException; import java.lang.String; public class liaotian extends JFrame{ pri…...

HBase整合Phoenix
文章目录 一、简介1、Phoenix定义2、Phoenix架构 二、安装Phoenix1、安装 三、Phoenix操作1、Phoenix 数据映射2、Phoenix Shell操作3、Phoenix JDBC操作3.1 胖客户端3.2 瘦客户端 四、Phoenix二级索引1、为什么需要二级索引2、全局索引(global index)3、…...

C# 委托/事件/lambda
概念 委托 定义委托编译器会自动生成一个类派生自System.MulticastDelegate 这个类包含4个方法:一个构造器、Invoke、BeginInvoke、EndInvoke。 调用委托的时候实际上执行的是 Invoke方法。 MulticastDelegate类有三个重要字段: _targetÿ…...

13款趣味性不错(炫酷)的前端动画特效及源码(预览获取)分享(附源码)
文字激光打印特效 基于canvas实现的动画特效,你既可以设置初始的打印文字也可以在下方输入文字可实现激光字体打印,精简易用。 预览获取 核心代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8&q…...
C# 友元程序集
1.友元程序集 使用友元程序集可以将internal成员提供给其他的友元程序集访问。 程序集FriendTest1.dll [assembly:InternalsVisibleTo("FriendTest2")] namespace FriendTest1 {internal class Friend{string name;public string Name > name;public Friend(str…...
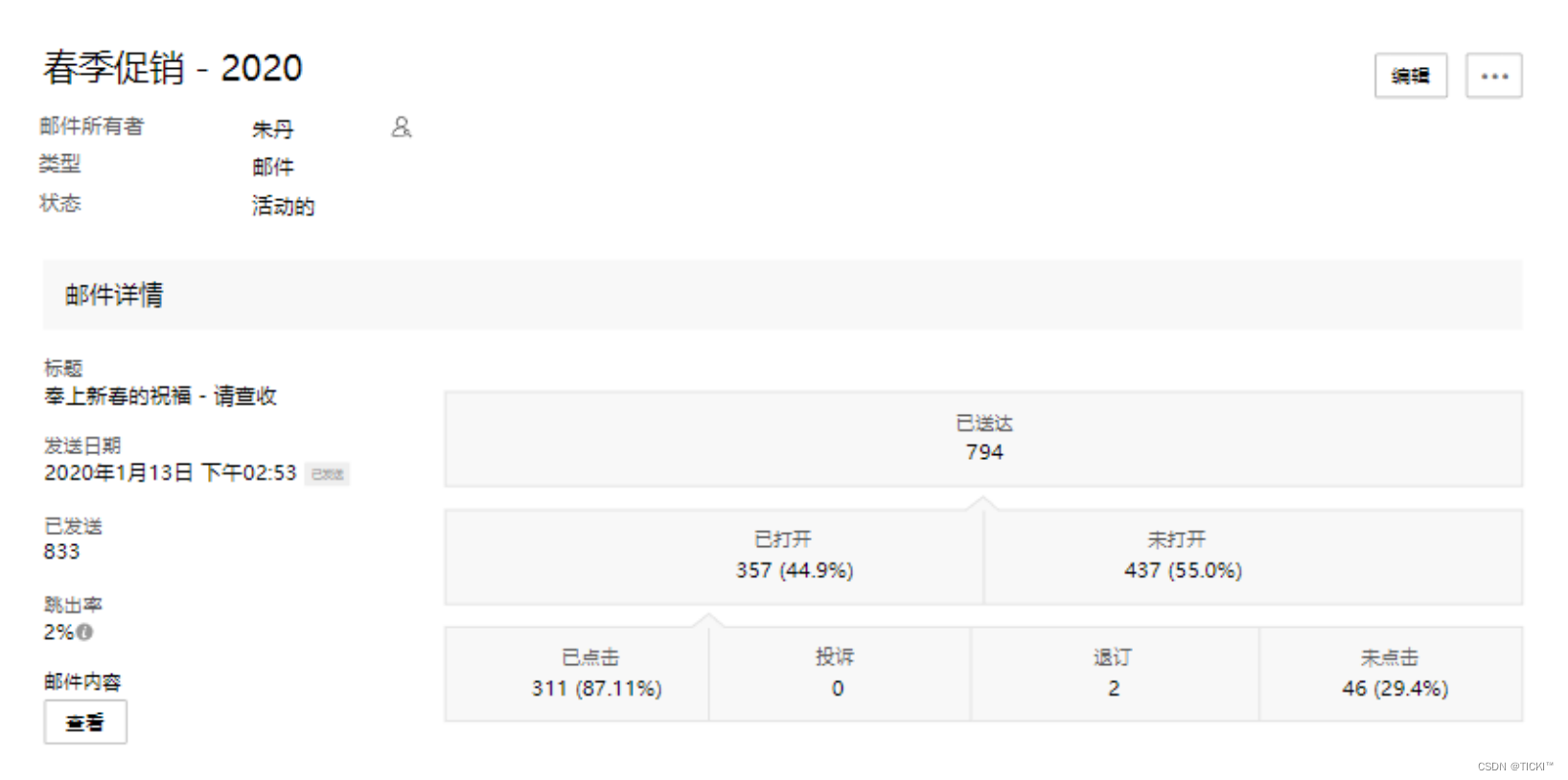
CRM系统的数据分析和报表功能对企业重要吗?
竞争日益激烈,企业需要更加高效地管理客户关系,以获取更多的商机。为此,许多企业选择使用CRM系统。在CRM中,数据分析功能扮演着重要的角色。下面就来详细说说,CRM系统数据分析与报表功能对企业来说重要吗? …...

【单体架构事务失效解决方式之___代理对象加锁】
单体架构__用户限买 一个id一单的多线程事务失效问题解决 背景介绍:有一种情况,我们在使用Synchronized的时候出现失效情况。 经过排查,是因为使用了this.当前对象,他现在使用的是目标对象加锁失效,使用代理对象加锁就…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...
