《深入理解计算机系统》学习笔记 - 第三课 - 浮点数
Floating Point 浮点数
文章目录
- Floating Point 浮点数
- 分数二进制示例
- 能代表的数
- 浮点数的表示方式
- 浮点数编码
- 规格化值
- 规格化值编码示例
- 非规格化的值
- 特殊值
- 示例
- IEEE 编码的一些特殊属性
- 四舍五入,相加,相乘
- 四舍五入
- 四舍五入的模式
- 二进制数的四舍五入
- 浮点数乘积
- 浮点数加法
- 浮点数的一些数学性质
- 浮点数在C中
- 类型转换的比较
- 《深入理解计算机系统》书籍学习笔记
浮点主要通过移动二进制小数点来表示尽可能大的取值范围,兼顾尽可能高的精度,同时还要受到位数有限的限制。
分数二进制示例
值 二进制表示 十进制
5 3/4 101.11 2^2 + 2^0 + 1/2^1 + 1/2^2
2 7/8 10.111 2^1 + 1/2^1 + 1/2^2 + 1/2^3
1 7/16 1.0111 2^0 + 1/2^2 + 1/2^3 + 1/2^4
- 分数除以2,就是小数点二进制右移1位。
- 乘以2, 就是小数点左移1位
- 数字0.111111111… 小于 1,无限接近于1
- 1/2 + 1/4 + 1/8 + … + 1/2^i + … -> 1.0
- 记为 1.0 - ε
能代表的数
-
只能精确地表示x/2k形式的数字
-
其他有理数有重复的位表示
值 二进制表达 十进制
1/3 0.01010101010101[01]... 1/2^2 + 1/2^4 + 1/2^6 + 1/2^8 + ...
1/5 0.001100110011[0011]... 1/2^3 + 1/2^4 + 1/2^7 + 1/2^8 + ...
1/10 0.0001100110011[0011]... 1/2^4 + 1/2^5 + 1/2^8 + 1/2^9 + ...
浮点数的表示方式
同一标准:
(–1)^s*M*2^E
看着是不是像二进制科学计数法。
- 符号位s: 决定了数是正数还是负数
- 显著值M(mantissa,小数部分): 通常是在[1.0,2.0]范围内的分数值。
- 指数E(exponent): 以2的幂表示值的权重
浮点数编码

- s 符号位
- exp 字段编码E(但是不等于E)
- frac 字段编码M (但是不等于M)
不同精度:
-
单精度:32 位(bits)
字段所占位数: s:exp:frac -> 1:8:23 -
双精度: 64 位(bits)
字段所占位数: s:exp:frac -> 1:11:52
规格化值
当exp != 000…0 , 并且exp != 111…1
指数编码有一个偏置值:E = Exp - Bias
Exp : exp字段,无符号值
Bias = 2^(k-1) -1
k 表示指数的位数
-
取值范围
单精度:k=8, Bias = 2^(8-1) - 1 = 127 (1 <= Exp <= 254, -126 <= E <= 127)
双精度: k=11,Bias = 2^(11-1) - 1 = 1023 (1 <= Exp <= 2046, -1022 <= E <= 1023) -
用隐含前导编码的有效数 1: M = 1.xxxxxx 二进制
xxxxx: 表示frac 字段编码
最小值:frac = 000…0(M=1.0)
最大值:frac = 111…1(M=2.0-ε)
注意: M 是固定前面有一个1,所以最小值才是1开始。
规格化值编码示例
-
值
Float F = 15213.0
15213 十进制 = 11101101101101 二进制
= 1.1101101101101 * 2^13 科学计数法 -
有效数
M(小数) = 1.1101101101101 二进制
frac(小数部分编码) = 1101101101101 0000000000 二进制 -
指数
E = 13
Bias = 127
Exp = 140 = 10001100 二进制 -
结果

非规格化的值
非规格化条件:exp = 000…0
指数值:E = 1 - Bias(注意:不是E = 0 - Bias)
以隐含前导0编码的有效数:M = 0.xxx…x
案例:
- exp = 000…0, frac = 000…0
代表0值 - exp = 000…0, frac != 000…0
最接近0.0的数字。
平均间隔。
特殊值
特殊值条件:exp = 111…1
案例:
-
exp = 111…1, frac = 000…0
代表无穷大。
操作溢出。
例如:正无穷大:1.0/0.0 = -1.0/-0.0 , 负无穷大:1.0/-0.0 -
exp = 111…1, frac != 000…0
Not-a-Number(NaN)
表示无法确定数值时的情况。
例如:sqrt(-1), 无穷大*0
示例
我们用简单的8位浮点数表示法,来理解浮点数。
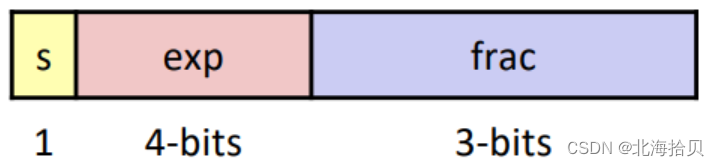
s: 1位符号位
exp: 4位指数位, 偏置位bias=2^(4-1)-1=7
frac: 3位小数位
s exp frac E Value 计算 备注
0 0000 000 -6 0 (-1)^0 * 0 * 2^(-6)
0 0000 001 -6 1/8*1/64 = 1/512 (-1)^0 * 2^(-3) * 2^(-6) // 最接近0值
0 0000 010 -6 2/8*1/64 = 2/512 (-1)^0 * 2^(-2) * 2^(-6)
…
0 0000 110 -6 6/8*1/64 = 6/512 (-1)^0 * 2^(-1)*2^(-2) * 2^(-6)
0 0000 111 -6 7/8*1/64 = 7/512 (-1)^0 * 2^(-1)*2^(-2)* 2^(-3) * 2^(-6) // 最大的非规格化值
0 0001 000 -6 8/8*1/64 = 8/512 (-1)^0 * 1 * 2^(-6) // 最小的规格化值
0 0001 001 -6 9/8*1/64 = 9/512 (-1)^0 * (1 + 2^(-3)) * 2^(-6)
…
0 0110 110 -1 14/8*1/2 = 14/16 (-1)^0 * (1 + 2^(-1)*2^(-2)) * 2^(-1)
0 0110 111 -1 15/8*1/2 = 15/16 (-1)^0 * (1 + 2^(-1)*2^(-2)* 2^(-3)) * 2^(-1) // 最接近1的(小于1的数)
0 0111 000 0 8/8*1 = 1 (-1)^0 * 1 * 2^0
0 0111 001 0 9/8*1 = 9/8 (-1)^0 * (1 + 2^(-3)) * 2^0 // 最接近1的(大于1的数)
0 0111 010 0 10/8*1 = 10/8 (-1)^0 * (1 + 2^(-2)) * 2^0
…
0 1110 110 7 14/8*128 = 224 (-1)^0 * (1 + 2^(-1)*2^(-2)) * 2^7
0 1110 111 7 15/8*128 = 240 (-1)^0 * (1 + 2^(-1)*2^(-2)* 2^(-3)) * 2^7 // 最大的规格化数
0 1111 000 7 inf
值的计算公式:v = (–1)^s * M * 2^E
规格化数: E = Exp – Bias
非规格化数: E = 1 – Bias
IEEE 编码的一些特殊属性
-
浮点数(FP)的0值和整型0值一样
所有的位都是0 -
除了非数字(NaN)之外,你可以比较任何浮点数。
当作无符号数来比较。
四舍五入,相加,相乘
四舍五入
基本思想:
- 先计算得到一个准确的值
- 然后根据你期望的精度进行处理
- 如果指数太大的化,可能会溢出
- 可能需要四舍五入来满足小数位数(frac)
四舍五入的模式
$1.40 $1.60 $1.50 $2.50 –$1.50
向0舍入 $1 $1 $1 $2 –$1
向下舍入 $1 $1 $1 $2 –$2
向上舍入 $2 $2 $2 $3 –$1
向偶数舍入 $1 $2 $2 $2 –$2
向0舍入:向0的方向舍去小数。
向下舍入:类似向下取整
向上舍入:类似向上取整
向偶数舍入:在四舍五入的基础上,考虑向偶数靠近,主要是在中位数时的处理方式和四舍五入不同。
二进制数的四舍五入
奇数是1,0是偶数。
二进制中间数100…,十进制中间数是500…
精度时小数后两位:
Value Binary Rounded Action Rounded Value
2 3/32 10.000112 10.002 (<1/2—down) 2
2 3/16 10.001102 10.012 (>1/2—up) 2 1/4
2 7/8 10.111002 11.002 ( 1/2—up) 3
2 5/8 10.101002 10.102 ( 1/2—down) 2 1/2
浮点数乘积
相乘:((–1)^s1 * M1 * 2^E1) x ((–1)^s2 * M2 * 2^E2)
准确值:: (–1)^s * M * 2^E
符号位 s: s1 ^ s2
有效位 M: M1 x M2
指数位 E: E1 + E2
修正:
- 如果 M >= 2, M 右移,增加E
- 如果E 超出范围,溢出
- 四舍五入 M 来符合精度要求。
浮点数加法
相加:((–1)^s1 * M1 * 2^E1) + ((–1)^s2 * M2 * 2^E2)
假设:E1 > E2
准确值:: (–1)^s * M * 2^E
符号位 s, 有效位 M: 对齐相加
指数位E: E1
修正:
- 如果 M >= 2, 右移M, 增加E。(小数点右移)
- 如果 M < 1, 左移 M 的 k 个位置, 减少 E 的 k。(小数点左移)
- 如果E超出范围溢出
- 将 M 适应小数(frac)精度
浮点数的一些数学性质
浮点数加法的数学性质:
- 与阿贝尔群的比较
- 加法封闭: 满足
- 但是可能产生 无穷大和NaN
- 结合律:满足
- 交换律:不满足
- 进行四舍五入时,可能溢出和不精确
- (3.14+1e10)-1e10 = 0, 3.14+(1e10-1e10) = 3.14
- 每个元素都有可加逆:几乎满足
- 除了无穷大和NaN
- 加法封闭: 满足
- 单调性
- a ≥ b ⇒ a+c ≥ b+c : 几乎满足
- 除了无穷大和NaN
- a ≥ b ⇒ a+c ≥ b+c : 几乎满足
浮点数乘法的数学性质和加法是类似的。
浮点数在C中
无符号和有符号的转换,从未改变过位的表示(位上的实际值),只是改变了某些位的解释方式。
整数,单精度浮点数,双进度浮点数的转换,位的表示发生了变化(实际值改变了),会对位的值产生实际影响。
- double/float -> int
- 截取小数部分
- 就像向0舍入
- int -> double
精确的转换,只要int(32) <= 53 位大小。 - int -> float
将会进行四舍五入操作。
类型转换的比较
三个不同类型的变量:
int x = …;
float f = …;
double d = …;
一些特性的比较:
* x == (int)(float) x // false
• x == (int)(double) x // true
• f == (float)(double) f // true
• d == (double)(float) d // false
• f == -(-f); // true
• 2/3 == 2/3.0 // false. 2/3=0 整数, 2/3.0 是浮点数。
• d < 0.0 ⇒ ((d*2) < 0.0) // true, 浮点数即使溢出也是负无穷大数
• d > f ⇒ -f > -d // true, 单调性
• d * d >= 0.0 // true
• (d+f)-d == f // false, 不满足结合律
《深入理解计算机系统》书籍学习笔记
《深入理解计算机系统》学习笔记 - 第一课 - 课程简介
《深入理解计算机系统》学习笔记 - 第二课 - 位,字节和整型
《深入理解计算机系统》学习笔记 - 第三课 - 位,字节和整型
《深入理解计算机系统》学习笔记 - 第四课 - 浮点数
相关文章:

《深入理解计算机系统》学习笔记 - 第三课 - 浮点数
Floating Point 浮点数 文章目录 Floating Point 浮点数分数二进制示例能代表的数浮点数的表示方式浮点数编码规格化值规格化值编码示例 非规格化的值特殊值 示例IEEE 编码的一些特殊属性四舍五入,相加,相乘四舍五入四舍五入的模式二进制数的四舍五入 浮…...

总结:服务器批量处理http请求的大致流程
总结:服务器批量处理http请求的大致流程 一客户端发起请求:可以多个请求同时发送二Web服务器解析请求(如:Nginx):可以多个请求同时解析三Servlet容器接收请求(如:tomcat)…...
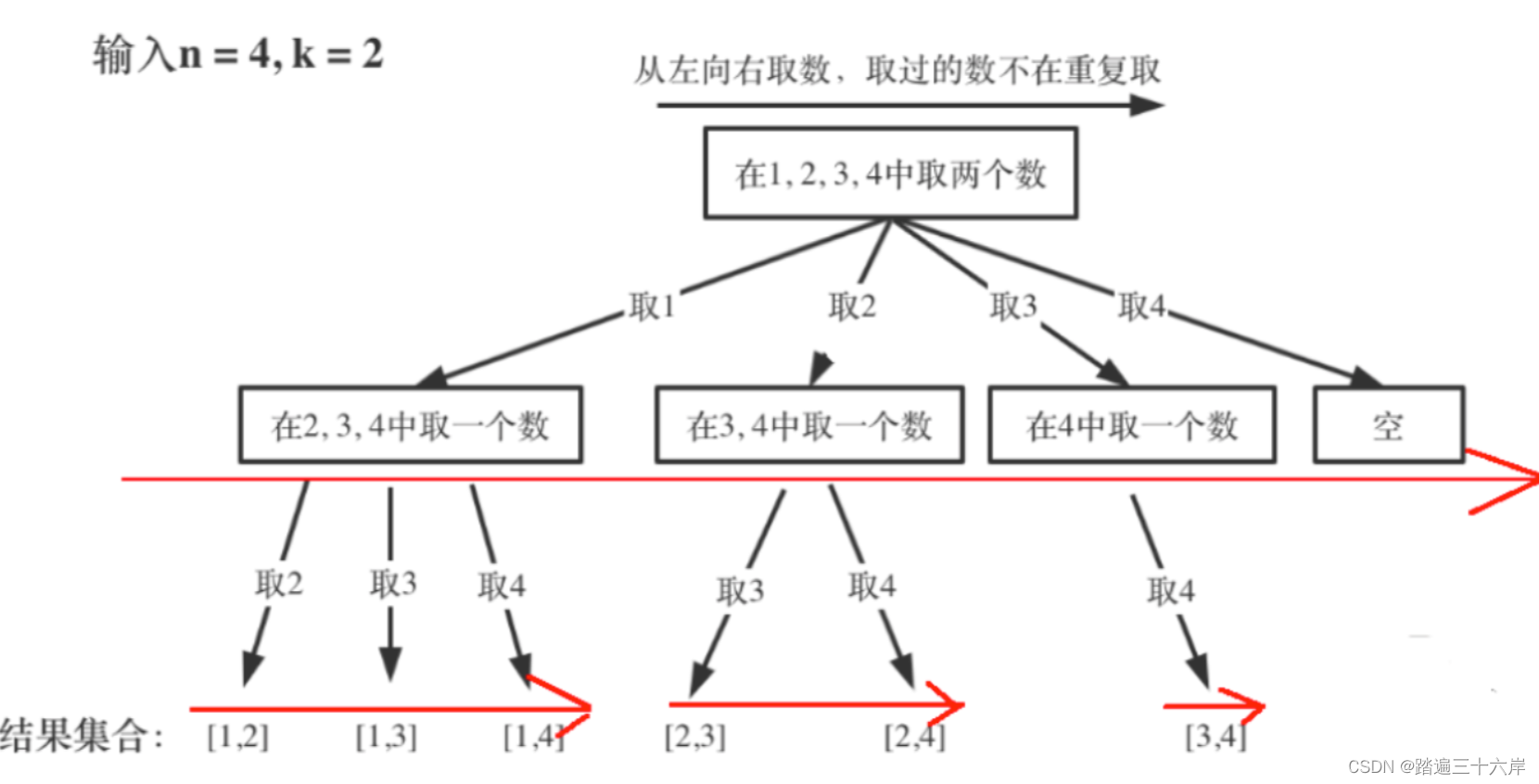
算法通关村第十八关-青铜挑战回溯是怎么回事
大家好我是苏麟 , 今天聊聊回溯是怎么个事 . 回溯是最重要的算法思想之一,主要解决一些暴力枚举也搞不定的问题,例如组合、分割、子集、排列,棋盘等。从性能角度来看回溯算法的效率并不高,但对于这些暴力都搞不定的算法能出结果就…...
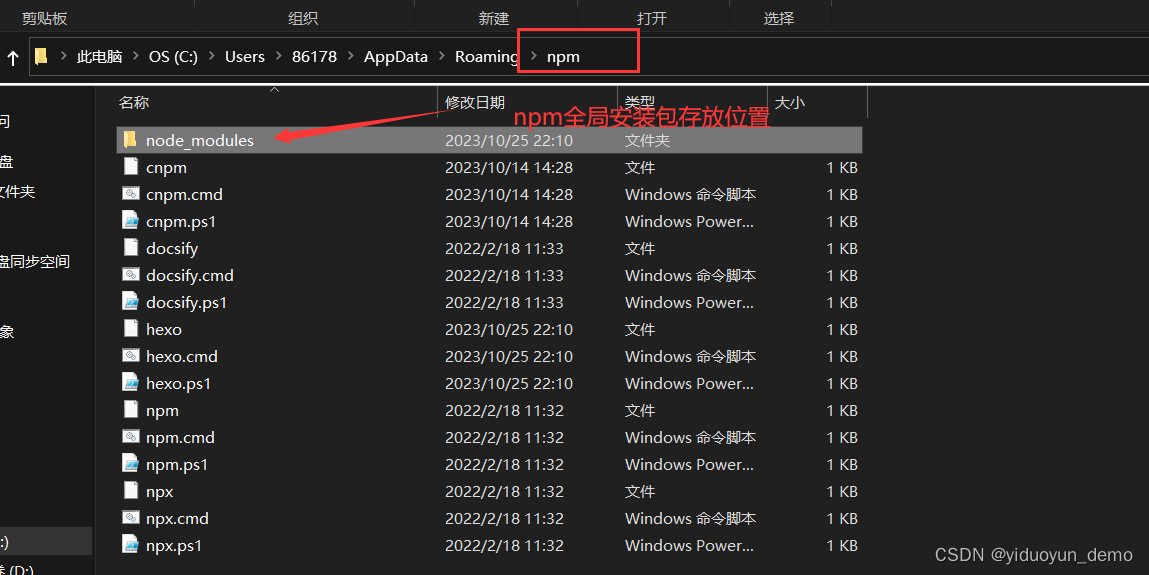
区分node,npm,nvm
目录 一,nodejs二,npm三,nvm 区分node,npm,nvm 几年前学习前端的时候学习的就是htmlcssjs 三件套。 现在只学习这些已经不能满足需要了。 一,nodejs nodejs是编程语言javascript运行时环境。(比…...

7-2 小霸王
幼儿园的老师给几位小朋友等量的长方体橡皮泥,但有个小朋友(小霸王)觉得自己的橡皮泥少了,就从另一个小朋友那里抢了一些。请问,是哪个小霸王抢了哪个小朋友的橡皮泥? 输入格式: 测试数据有多组。对于每组…...

Linux内核上游提交完整流程及示例
参考博客文章: 向linux内核提交代码 - 知乎 一、下载Linux内核源码 通过git下载Linux内核源码,具体命令如下: git clone git://git.kernel.org/pub/scm/linux/kernel/git/torvalds/linux.git 实际命令及结果如下: penghaoDin…...

TS学习——快速入门
TypeScript简介 TypeScript是JavaScript的超集。它对JS进行了扩展,向JS中引入了类型的概念,并添加了许多新的特性。TS代码需要通过编译器编译为JS,然后再交由JS解析器执行。TS完全兼容JS,换言之,任何的JS代码都可以直…...

深圳锐科达风力发电广播对讲解决方案
深圳锐科达风力发电广播对讲解决方案 风力发电对讲通常是在风塔的底部与机舱室安装一键对讲终端,可以一键呼叫控制中心值班人员,结构简单,组网方便,设备可以接入局域网或广域网构成功能应急呼叫系统。 系统实现的功能࿱…...

极智芯 | 解读国产AI算力 璧仞产品矩阵
欢迎关注我,获取我的更多经验分享 大家好,我是极智视界,本文分享一下 解读国产AI算力 璧仞产品矩阵。 璧仞在国产 AI 芯领域就是 "迷" 一样的存在,你要说它在市场上的 "建树" 泛善可陈的话,它又 "赫然" 在美国芯片禁令名单中。而这一切的一…...

Echarts折线图常见问题及案例代码
前言 ECharts 是一个使用 JavaScript 实现的开源可视化库,它可以帮助用户以简单的方式创建复杂的时间序列、条形图、饼图、地图等图形。 初学者,可参考下我的另外两篇文章,从基础到深入,解读饼状图的运用。 ECharts初始案例(入门) ECharts之折线图 常见问题及案例代码 …...
javaTCP协议实现一对一聊天
我们首先要完成服务端,不然出错,运行也要先运行服务端,如果不先连接服务端,就不监听,那客户端不知道连接谁 服务端 package d21z; import java.awt.BorderLayout; import java.awt.event.ActionEvent; import java.a…...
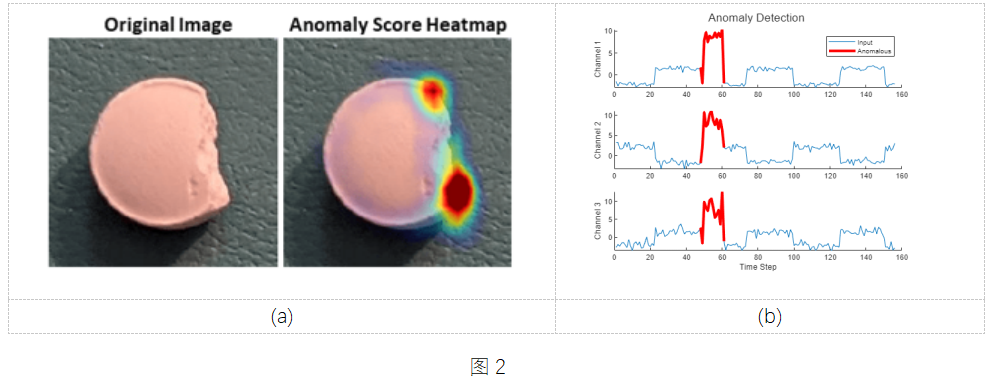
机器学习应用 | 使用 MATLAB 进行异常检测(上)
异常检测任务,指的是检测偏离期望行为的事件或模式,可以是简单地检测数值型数据中,是否存在远超出正常取值范围的离群值,也可以是借助相对复杂的机器学习算法识别数据中隐藏的异常模式。 在不同行业中,异常检测的典型…...

Java -jar参数详解
java -jar 命令用于执行打包成可执行 JAR 文件的 Java 应用程序。在运行时,你可以通过命令行传递参数给这个应用程序。 1. -jar 参数: 说明: 指定要执行的 JAR 文件。示例:java -jar your-application.jar 2. -D 参数ÿ…...
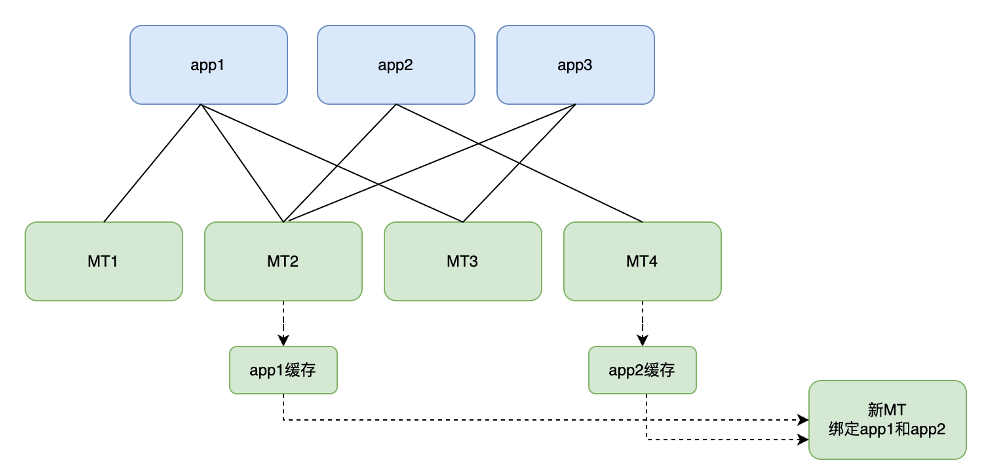
RocksDB 在 vivo 消息推送系统中的实践
作者:vivo 互联网服务器团队 - Zeng Luobin 本文主要介绍了 RocksDB 的基础原理,并阐述了 RocksDB 在vivo消息推送系统中的一些实践,通过分享一些对 RocksDB 原生能力的探索,希望可以给使用RocksDB的读者带来启发。 一、背景 在…...
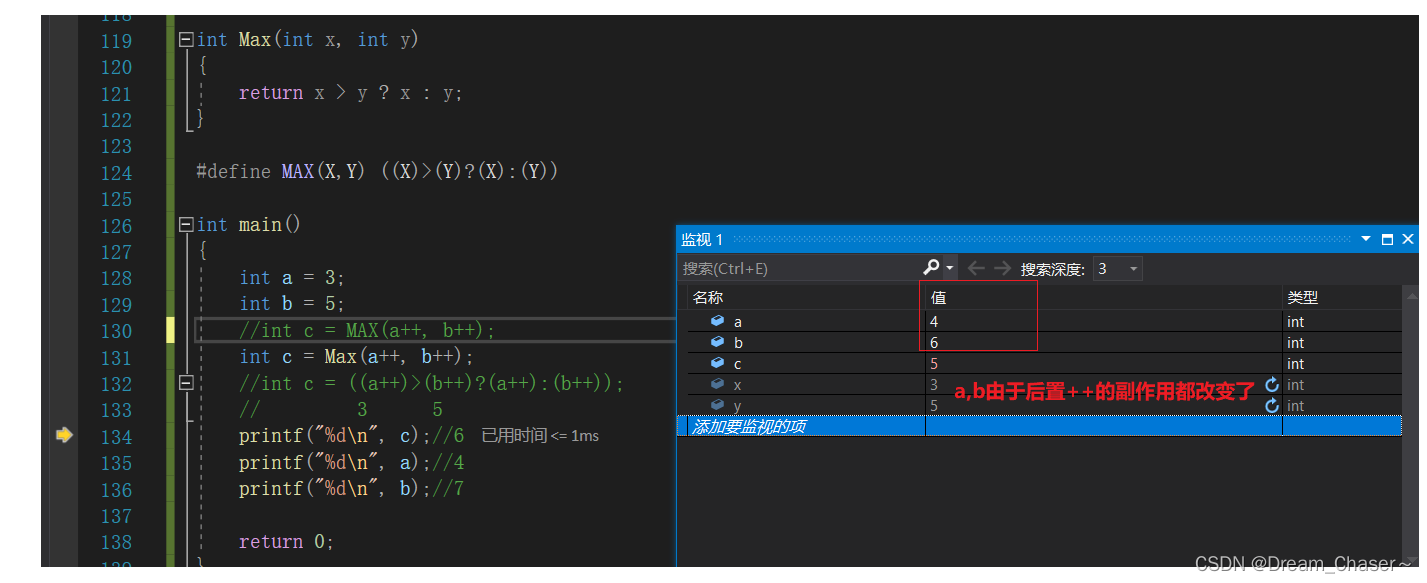
【C进阶】C程序是怎么运作的呢?-- 程序环境和预处理(上)
前言: 由于c语言的程序编译链接的这块知识点不清楚,回来复习一遍,以便于好理解c知识,我会尽快更新下一篇文章。 目录 1.程序的翻译环境和执行环境 2.翻译环境(编译链接) 编译(编译器…...

点滴生活记录1
2023/10/10 今天骑小电驴上班,带着小鸭子一起。路上的时候,我给小鸭子说,你要帮我看着点路,有危险的时候提醒我,也就刚说完没几分钟,一个没注意,直接撞到一个拦路铁墩子上,车子连人歪…...

gitea仓库迁移
(1)先安装git,再直接将源机器上的gitea文件夹复制到新机器上。这样原始数据及账号信息都还在。 (2)根据实际情况修改gitea\custom\conf\app.ini文件夹下app.ini文件的相关路径。 (3)如下命令启…...
〖大前端 - 基础入门三大核心之JS篇㊽〗- BOM特效开发
说明:该文属于 大前端全栈架构白宝书专栏,目前阶段免费,如需要项目实战或者是体系化资源,文末名片加V!作者:哈哥撩编程,十余年工作经验, 从事过全栈研发、产品经理等工作,目前在公司…...

【扩散模型】ControlNet从原理到实战
ControlNet从原理到实战 ControlNet原理ControlNet应用于大型预训练扩散模型ControlNet训练过程ControlNet示例1 ControlNet与Canny Edge2. ControlNet与Depth3. ControlNet与M-LSD Lines4. ControlNet与HED Boundary ControlNet实战Canny Edge实战Open Pose 小结参考资料 Cont…...

AI并行计算:CUDA和ROCm
1 介绍 1.1 CUDA CUDA(Compute Unified Device Architecture)是Nvidia于2006年推出的一套通用并行计算架构,旨在解决在GPU上的并行计算问题。其易用性和便捷性能够方便开发者方便的进行GPU编程,充分利用GPU的并行能力࿰…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...
