算法-贪心思想

贪心的思想非常不好解释，而且越使用权威的语言解释越难懂。而且做题的时候根据自己的理解可能直接做出来，但是非要解释一下怎么使用的贪心的话，就懵圈了。一般来说，贪心的题目没有固定的套路，一题一样，不过好在大部分的贪心算法题不是特别难。

一、贪心思想 

定义

指在对问题进行求解时，在每一步选择中都采取最好或者最优(即最有利)的选择，从而希望能够导致结果是最好或者最优的算法。

注意：贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解)，但是都是相对近似(接近)最优解的结果。

 

性质

1. 最优子结构性质

最优子结构性质是指问题的最优解包含了其子问题的最优解。

也就是说，在使用贪心算法解决问题时，我们可以通过子问题的最优解来构建全局最优解。通过将问题分解为各个子问题，并以递归的方式解决子问题，最终可以获得整体的最优解😁。

 

2. 贪心选择性质

贪心选择性质是指在每一步选择中，都采取当前最好的选择，而不考虑未来的影响。也就是说，我们每次做出局部最优的选择，希望这些局部最优解最终能够导致全局最优解。

注意：在选择使用贪心算法解决问题时，必须确保问题满足这两个性质。

应用场景

• 排序问题：选择排序、拓扑排序

• 优先队列：堆排序

• 赫夫曼压缩编码

• 图里的Prim、Fruskal和Dijkstra算法

• 硬币找零问题🤭

• 部分背包问题

• 并查集的按大小或者高度合并问题或者排名

• 任务调度部分场景

• 一些复杂问题的近似算法

 

二、贪心例题 

1、分发饼干

LeetCode 455：假设你是一位很棒的家长，想要给你的孩子们一些小饼干🍪。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，将这个饼干 j 分配给孩子 i ，这孩子会满足。要求尽可能满足越多数量的孩子，并输出这个最大数值。

示例：

• 输入: g = [1,2,3], s = [1,1]

• 输出: 1

• 解释: 你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。所以你应该输出1。

分析：这里既要满足小孩的胃口，也不要造成饼干尺寸的浪费。大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子，那么就应该优先满足胃口大的。这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。

使用贪心策略，先将饼干数组和小孩数组排序。然后从后向前遍历小孩数组，用大饼干优先满足胃口大的，并统计满足小孩数量就可以了。

 

public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int count = 0;int start = s.length - 1;//遍历孩子的胃口for(int i = g.length - 1 ; i >=0 ; i--){if(start >= 0 && g[i] <= s[start]){start--;count++;}}return count;
}

 

2、柠檬水找零

LeetCode 860：在柠檬水摊上，每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。

注意，一开始你手头没有任何零钱。

给你一个整数数组 bills ，其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

示例：

• 输入：bills = [5,5,5,10,20]

• 输出：true

解释:

• 前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。

• 第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。

• 第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。由于所有客户都得到了正确的找零，所以我们输出 true。

分析：收钱找零的情况有三种：

1. 如果给的是5，那么直接收下。

2. 如果给的是10元，那么收下一个10，给出一个5，此时必须要有一个5才行。

3. 如果给的是20，那么优先消耗一个10元，再给一个5元。假如没有10元，则给出3个5元。

第三种情况还要再分析：如果给的是20，那么优先消耗一个10元，再给一个5元；还是给出3个5元？

答：肯定是有10就先给10，没有才给多个5。因为10只能给账单20找零，而5可以给账单10和账单20找零，5更万能😉！所以这里的局部最优就是遇到账单20，优先消耗美元10，完成本次找零。

这就是局部最优可以推出全局最优，代码如下：

public boolean lemonadeChange(int[] bills) {//仅代表5元和10元纸币的数量，而不是总金额int cash_5 = 0;int cash_10 = 0;for(int i = 0;i<bills.length;i++){if(bills[i]==5){cash_5++;}if(bills[i] == 10){cash_5--;cash_10++;}if(bills[i] == 20){if(cash_10 > 0){cash_10--;cash_5--;}else{cash_5 -= 3;}}//如果遍历这一位客户的钱之后，纸币数量需要为负数，则直接返回falseif(cash_5 < 0 || cash_10 < 0) return false;}return true;
}

就像老爹说的那样：不要被事物的表面现象所迷惑，这题的关键是某种纸币的数量，而不是面值。

 

3、分发糖果

LeetCode 135：n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。你需要按照以下要求，给这些孩子分发糖果：

• 每个孩子至少分配到 1 个糖果。

• 相邻两个孩子评分更高的孩子会获得更多的糖果。

• 请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目。

示例 1：

• 输入：ratings = [1,0,2]

• 输出：5

• 解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。

示例 2：

• 输入：ratings = [1,2,2]

• 输出：4

• 解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

分析：首先我们来看这个题是什么意思。假如有5个孩子，因为每个孩子至少一个糖果，所以一定要花出去的最少糖果是{1,1,1,1,1} 一共5个。

然后是相邻孩子评分更高的能获得更多的糖果。假如评分为{1,2,3,2}，则最少花出去的糖果为{1,2,3,1}，因为前三个评分在增加，则糖果必须递增，因此分别要发的糖果最少为{1,2,3}个，最后一个因为评分低了，所以我们给最少1个。

另外，假如评分相等，例如{1,2,2,2,2,}，根据题目要求，则后面重复的都给一个的就行了，也就是分别给{1,2,1,1,1}个。

综上，可以从左向后依次比较，确定第一轮要预发的糖果数量，只要右边的比左边的大，就一直加1；如果右边比左边小，就设置为1 ，然后继续向右比较。结果如下：

 

 但是，题目是要求相邻的孩子评分高的孩子必须获得更多的糖果，上面序列的后面几个评分为 4 、3、 2 但是得到的糖果却是一样的，那怎么办呢？

很简单，在上面的基础上，再从右向左走一轮。如果左边的比右边的小，则不管。如果左边的比右边的大，则不是简单的加一，而是要在{i+1}的基础上，先加1再赋值给{i}。看例子：

最后四个评分为 {5 4 3 2 }，第一轮结束之后应该发的糖果为left={2,1,1,1}。如果只考虑从右向左的时候，很显然：

• 最后一个评分为2得到1个糖果

• 倒数第二个评分为3，得到2个糖果

• 倒数第三个评分为4，得到2+1=3个糖果

• 倒数第四个评分为5，得到3+1=4个糖果

因此最后四个的 right={4,3,2,1}，接下来每个位置i我们只要从 left[i] 和 right[i] 中选最大就行了。这里其实不用两个数组，一个数组更新两次即可，首先从左向后给数组 candyVec 赋值，然后再从右向左更新数组元素，每次赋值之前先比较一下取max即可。如下图：

 

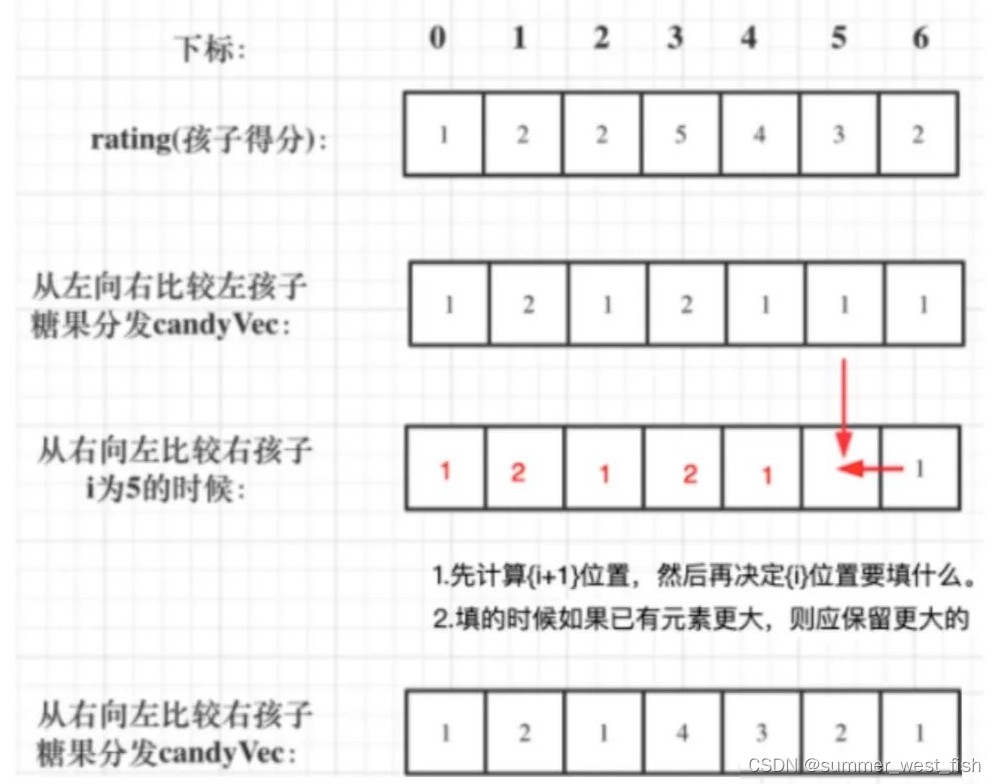
所以代码如下：

public int candy(int[] ratings) {int[] candyVec = new int[ratings.length];candyVec[0] = 1;for (int i = 1; i < ratings.length; i++) {if (ratings[i] > ratings[i - 1]) {candyVec[i] = candyVec[i - 1] + 1;} else {candyVec[i] = 1;}}for (int i = ratings.length - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1]) {// 屏蔽不是连续数据的情况，candyVec[i]=4 & candyVec[i + 1]=2candyVec[i] = Math.max(candyVec[i], candyVec[i + 1] + 1);}}int ans = 0;for (int s : candyVec) {ans += s;}return ans;
}