[足式机器人]Part4 南科大高等机器人控制课 Ch03 Operator View of Rigid-Body Transformation
本文仅供学习使用
本文参考:
B站:CLEAR_LAB
笔者带更新-运动学
课程主讲教师:
Prof. Wei Zhang
南科大高等机器人控制课 Ch03 Operator View of Rigid-Body Transformation
- 1. Rotation Operation via Differential Equation
- 1.1 Skew Symmetric Matrices
- 1.2 Rotation Operation via Differential Equation
- 1.3 Raotation Matrix as a Rotation Operator
- 2. Rotation Operation in Different Frames
- 2.1 Rotation Martix Properties
- 2.2 Rotation Operation in Different Frames
- 3. Rigid-Body Operation via Diffeential Equation
- 3.1 SE(3)
- 3.2 se(3)
- 4. Homogeneous Transformation Matrix as Rigid-Body Operator
- 5. Rigid-Body Operation of Screw Axis
1. Rotation Operation via Differential Equation
1.1 Skew Symmetric Matrices
Recall that cross product is a special linear transformation.
For any ω ⃗ ∈ R 3 \vec{\omega}\in \mathbb{R} ^3 ω∈R3, there is a matrix ω ⃗ ~ ∈ R 3 × 3 \tilde{\vec{\omega}}\in \mathbb{R} ^{3\times 3} ω~∈R3×3 such that ω ⃗ × R ⃗ = ω ⃗ ~ R ⃗ \vec{\omega}\times \vec{R}=\tilde{\vec{\omega}}\vec{R} ω×R=ω~R
ω ⃗ = [ ω 1 ω 2 ω 3 ] ⟷ ω ⃗ ~ = [ 0 − ω 3 ω 2 ω 3 0 − ω 1 − ω 2 ω 1 0 ] \vec{\omega}=\left[ \begin{array}{c} \omega _1\\ \omega _2\\ \omega _3\\ \end{array} \right] \longleftrightarrow \tilde{\vec{\omega}}=\left[ \begin{matrix} 0& -\omega _3& \omega _2\\ \omega _3& 0& -\omega _1\\ -\omega _2& \omega _1& 0\\ \end{matrix} \right] ω= ω1ω2ω3 ⟷ω~= 0ω3−ω2−ω30ω1ω2−ω10
Note that a ⃗ ~ = − a ⃗ ~ T \tilde{\vec{a}}=-\tilde{\vec{a}}^{\mathrm{T}} a~=−a~T (called skew stmmetric)
ω ⃗ ~ \tilde{\vec{\omega}} ω~ is called a skew-symmetric matrix representation of the vector ω ⃗ \vec{\omega} ω
The set of skew-symmetric matrices in : s o ( n ) ≜ { S ∈ R n × n : S T = − S } so\left( n \right) \triangleq \left\{ S\in \mathbb{R} ^{n\times n}:S^{\mathrm{T}}=-S \right\} so(n)≜{S∈Rn×n:ST=−S}
We are interested in case n = 2 , 3 n=2,3 n=2,3
Rotation matrix ∈ S O ( 3 ) { R T R = E , det ( R ) = 1 } \in SO\left( 3 \right) \left\{ R^{\mathrm{T}}R=E,\det \left( R \right) =1 \right\} ∈SO(3){RTR=E,det(R)=1}
1.2 Rotation Operation via Differential Equation
- Consider a point initially located at R ⃗ p 0 \vec{R}_{p_0} Rp0 at time t = 0 t=0 t=0
- Rotate the point with unit angular velocity ω ^ \hat{\omega} ω^. Assuming the rotation axis passing through the origin, the motion is describe by
R ⃗ ˙ p ( t ) = ω ^ × R ⃗ p = ω ^ ~ R ⃗ p ( t ) , p ( 0 ) = p 0 \dot{\vec{R}}_p\left( t \right) =\hat{\omega}\times \vec{R}_p=\tilde{\hat{\omega}}\vec{R}_p\left( t \right) ,p\left( 0 \right) =p_0 R˙p(t)=ω^×Rp=ω^~Rp(t),p(0)=p0
linear velocity at time t t t, recall x ˙ = A x , x ( 0 ) = x 0 ⇒ x ( t ) = e A t x 0 \dot{x}=Ax,x\left( 0 \right) =x_0\Rightarrow x\left( t \right) =e^{At}x_0 x˙=Ax,x(0)=x0⇒x(t)=eAtx0 - This is a linear ODE with solution : R ⃗ ˙ p ( t ) = ω ^ ~ R ⃗ p ( t ) ⇒ R ⃗ ˙ p ( t ) = e ω ^ ~ t R ⃗ p 0 \dot{\vec{R}}_p\left( t \right) =\tilde{\hat{\omega}}\vec{R}_p\left( t \right) \Rightarrow \dot{\vec{R}}_p\left( t \right) =e^{\tilde{\hat{\omega}}t}\vec{R}_{p_0} R˙p(t)=ω^~Rp(t)⇒R˙p(t)=eω^~tRp0
- After t = θ t=\theta t=θ, the point has been rotated by θ \theta θ degree. Note R ⃗ ˙ p ( θ ) = e ω ^ ~ θ R ⃗ p 0 \dot{\vec{R}}_p\left( \theta \right) =e^{\tilde{\hat{\omega}}\theta}\vec{R}_{p_0} R˙p(θ)=eω^~θRp0, e ω ^ ~ θ e^{\tilde{\hat{\omega}}\theta} eω^~θ is rotation operator
- R o t ( ω ^ , θ ) ≜ e ω ^ ~ θ \mathrm{Rot}\left( \hat{\omega},\theta \right) \triangleq e^{\tilde{\hat{\omega}}\theta} Rot(ω^,θ)≜eω^~θ can be viewed as a rotation operator that rotates a point about ω ^ \hat{\omega} ω^ through θ \theta θ degree
The discussion holds for any reference frame
1.3 Raotation Matrix as a Rotation Operator
- Theorem: Every rotation matrix R R R can be written as R = R o t ( ω ^ , θ ) ≜ e ω ^ ~ θ ∈ S O ( 3 ) { R T R = E , det ( R ) = 1 } R=\mathrm{Rot}\left( \hat{\omega},\theta \right) \triangleq e^{\tilde{\hat{\omega}}\theta}\in SO\left( 3 \right) \left\{ R^{\mathrm{T}}R=E,\det \left( R \right) =1 \right\} R=Rot(ω^,θ)≜eω^~θ∈SO(3){RTR=E,det(R)=1}, i.e. , it represents a rotation operation about ω ^ \hat{\omega} ω^ by θ \theta θ
- We have seen how to use R R R to represent frame orientation and change of coordinate between different frames. They are quite different from the operator interpretation of R R R
- To apply the rotation operation, all the vectors / matrices have to be expressed in the same refrence frame
For example, assume R = [ 1 0 0 0 0 − 1 0 1 0 ] = R o t ( x ^ , π 2 ) R=\left[ \begin{matrix} 1& 0& 0\\ 0& 0& -1\\ 0& 1& 0\\ \end{matrix} \right] =\mathrm{Rot}\left( \hat{x},\frac{\pi}{2} \right) R= 1000010−10 =Rot(x^,2π)
Consider a relation q = R p q=Rp q=Rp:
- Change reference frame interpretation : two frames { A } , { B } \left\{ A \right\} ,\left\{ B \right\} {A},{B} , one physical Point a a a
R R R : orientation of { B } \left\{ B \right\} {B} relative to { A } \left\{ A \right\} {A} : i.e. R = [ Q B A ] R=\left[ Q_{\mathrm{B}}^{A} \right] R=[QBA]
then : p = a B , q = a A , q = R p ⇒ a A = [ Q B A ] a B p=a^B,q=a^A,q=Rp\Rightarrow a^A=\left[ Q_{\mathrm{B}}^{A} \right] a^B p=aB,q=aA,q=Rp⇒aA=[QBA]aB- Rotation operator interpretation : one frame and two points
a → a ′ , p = a A , q = a ′ A ⇒ a ′ A = R a A a\rightarrow a^{\prime},p=a^A,q={a^{\prime}}^A\Rightarrow {a^{\prime}}^A=Ra^A a→a′,p=aA,q=a′A⇒a′A=RaAConsider the frame operation:
- Change of reference frame :
Have one “frame object”, two reference frames
Frame object { A } \left\{ A \right\} {A}, orientation in { O } \left\{ O \right\} {O} , is R A O , R A B R_{\mathrm{A}}^{O},R_{\mathrm{A}}^{B} RAO,RAB, ⇒ R A O = R B O R A B = R R A B \Rightarrow R_{\mathrm{A}}^{O}=R_{\mathrm{B}}^{O}R_{\mathrm{A}}^{B}=RR_{\mathrm{A}}^{B} ⇒RAO=RBORAB=RRAB- Rotation a frame : R ′ A = R R A {R^{\prime}}_A=RR_A R′A=RRA
two frame objects, one refrence frame
more precisely : R ′ A = R R A ⇒ R A ′ O = R R A O {R^{\prime}}_A=RR_A\Rightarrow R_{\mathrm{A}^{\prime}}^{O}=RR_{\mathrm{A}}^{O} R′A=RRA⇒RA′O=RRAO
2. Rotation Operation in Different Frames
2.1 Rotation Martix Properties
[ Q ] [ Q ] T = E \left[ Q \right] \left[ Q \right] ^{\mathrm{T}}=E [Q][Q]T=E
[ Q 1 ] [ Q 2 ] ∈ S O ( 3 ) , i f [ Q 1 ] , [ Q 2 ] ∈ S O ( 3 ) \left[ Q_1 \right] \left[ Q_2 \right] \in SO\left( 3 \right) ,if\,\,\left[ Q_1 \right] ,\left[ Q_2 \right] \in SO\left( 3 \right) [Q1][Q2]∈SO(3),if[Q1],[Q2]∈SO(3): product of two rotation matrices is also a rotation matrix
p , q ∈ R 3 , ∥ [ Q ] R ⃗ p − [ Q ] R ⃗ q ∥ 2 = ∥ [ Q ] ( R ⃗ p − R ⃗ q ) ∥ 2 = ( R ⃗ p − R ⃗ q ) T [ Q ] T [ Q ] ( R ⃗ p − R ⃗ q ) = ∥ R ⃗ p − R ⃗ q ∥ 2 p,q\in \mathbb{R} ^3,\left\| \left[ Q \right] \vec{R}_p-\left[ Q \right] \vec{R}_{\mathrm{q}} \right\| ^2=\left\| \left[ Q \right] \left( \vec{R}_p-\vec{R}_{\mathrm{q}} \right) \right\| ^2=\left( \vec{R}_p-\vec{R}_{\mathrm{q}} \right) ^{\mathrm{T}}\left[ Q \right] ^{\mathrm{T}}\left[ Q \right] \left( \vec{R}_p-\vec{R}_{\mathrm{q}} \right) =\left\| \vec{R}_p-\vec{R}_{\mathrm{q}} \right\| ^2 p,q∈R3, [Q]Rp−[Q]Rq 2= [Q](Rp−Rq) 2=(Rp−Rq)T[Q]T[Q](Rp−Rq)= Rp−Rq 2
∥ R ⃗ p − R ⃗ q ∥ = ∥ [ Q ] R ⃗ p − [ Q ] R ⃗ q ∥ \left\| \vec{R}_p-\vec{R}_{\mathrm{q}} \right\| =\left\| \left[ Q \right] \vec{R}_p-\left[ Q \right] \vec{R}_{\mathrm{q}} \right\| Rp−Rq = [Q]Rp−[Q]Rq : rotation operator preserves distance
[ Q ] ( v ⃗ × w ⃗ ) = [ Q ] v ⃗ × [ Q ] w ⃗ \left[ Q \right] \left( \vec{v}\times \vec{w} \right) =\left[ Q \right] \vec{v}\times \left[ Q \right] \vec{w} [Q](v×w)=[Q]v×[Q]w
[ Q ] w ⃗ ~ [ Q ] T = [ Q ] w ⃗ ~ \left[ Q \right] \tilde{\vec{w}}\left[ Q \right] ^{\mathrm{T}}=\widetilde{\left[ Q \right] \vec{w}} [Q]w~[Q]T=[Q]w —— important
2.2 Rotation Operation in Different Frames
Consider two frames { A } \left\{ A \right\} {A} and { B } \left\{ B \right\} {B}, the actual numerical values of the operator R o t ( ω ^ , θ ) \mathrm{Rot}\left( \hat{\omega},\theta \right) Rot(ω^,θ) depend on both the reference frame to repersent ω ^ \hat{\omega} ω^ and the reference frame to represent the operator itself
Consider a rotation axis ω ^ \hat{\omega} ω^ (coordinate free vector), with { A } \left\{ A \right\} {A} - frame coordinate ω ^ A \hat{\omega}^A ω^A and { B } \left\{ B \right\} {B} - frame. We know ω ⃗ A = [ Q B A ] ω ⃗ B \vec{\omega}^A=\left[ Q_{\mathrm{B}}^{A} \right] \vec{\omega}^B ωA=[QBA]ωB
Let B R o t ( B ω ^ , θ ) ^B\mathrm{Rot}\left( ^B\hat{\omega},\theta \right) BRot(Bω^,θ) and A R o t ( A ω ^ , θ ) ^A\mathrm{Rot}\left( ^A\hat{\omega},\theta \right) ARot(Aω^,θ) be the two rotation matrices, representing the same rotation operatioon R o t ( ω ^ , θ ) \mathrm{Rot}\left( \hat{\omega},\theta \right) Rot(ω^,θ) in frames { A } \left\{ A \right\} {A} and { B } \left\{ B \right\} {B}
We have the relation : A R o t ( A ω ^ , θ ) = [ Q B A ] B R o t ( B ω ^ , θ ) [ Q A B ] ^A\mathrm{Rot}\left( ^A\hat{\omega},\theta \right) =\left[ Q_{\mathrm{B}}^{A} \right] ^B\mathrm{Rot}\left( ^B\hat{\omega},\theta \right) \left[ Q_{\mathrm{A}}^{B} \right] ARot(Aω^,θ)=[QBA]BRot(Bω^,θ)[QAB]
-
Approach 1 : two points p → p ′ ⇒ R ⃗ p ′ A = A R o t ( A ω ^ , θ ) R ⃗ p A p\rightarrow p^{\prime}\Rightarrow \vec{R}_{\mathrm{p}^{\prime}}^{A}=^A\mathrm{Rot}\left( ^A\hat{\omega},\theta \right) \vec{R}_{\mathrm{p}}^{A} p→p′⇒Rp′A=ARot(Aω^,θ)RpA
{ B } \left\{ B \right\} {B} - frame : R ⃗ p ′ B = B R o t ( B ω ^ , θ ) R ⃗ p B \vec{R}_{\mathrm{p}^{\prime}}^{B}=^B\mathrm{Rot}\left( ^B\hat{\omega},\theta \right) \vec{R}_{\mathrm{p}}^{B} Rp′B=BRot(Bω^,θ)RpB
⇒ [ Q B A ] R ⃗ p ′ B = [ Q B A ] B R o t ( B ω ^ , θ ) R ⃗ p B ⇒ R ⃗ p ′ A = [ Q B A ] B R o t ( B ω ^ , θ ) [ Q B A ] R ⃗ p A ⇒ A R o t ( A ω ^ , θ ) = [ Q B A ] B R o t ( B ω ^ , θ ) [ Q B A ] \Rightarrow \left[ Q_{\mathrm{B}}^{A} \right] \vec{R}_{\mathrm{p}^{\prime}}^{B}=\left[ Q_{\mathrm{B}}^{A} \right] ^B\mathrm{Rot}\left( ^B\hat{\omega},\theta \right) \vec{R}_{\mathrm{p}}^{B}\Rightarrow \vec{R}_{\mathrm{p}^{\prime}}^{A}=\left[ Q_{\mathrm{B}}^{A} \right] ^B\mathrm{Rot}\left( ^B\hat{\omega},\theta \right) \left[ Q_{\mathrm{B}}^{A} \right] \vec{R}_{\mathrm{p}}^{A}\Rightarrow ^A\mathrm{Rot}\left( ^A\hat{\omega},\theta \right) =\left[ Q_{\mathrm{B}}^{A} \right] ^B\mathrm{Rot}\left( ^B\hat{\omega},\theta \right) \left[ Q_{\mathrm{B}}^{A} \right] ⇒[QBA]Rp′B=[QBA]BRot(Bω^,θ)RpB⇒Rp′A=[QBA]BRot(Bω^,θ)[QBA]RpA⇒ARot(Aω^,θ)=[QBA]BRot(Bω^,θ)[QBA] -
Approach 2 : for a ⃗ ∈ R 3 , a ⃗ ~ ∈ s o ( 3 ) , [ Q ] ∈ S O ( 3 ) \vec{a}\in \mathbb{R} ^3,\tilde{\vec{a}}\in so\left( 3 \right) ,\left[ Q \right] \in SO\left( 3 \right) a∈R3,a~∈so(3),[Q]∈SO(3)
⇒ [ Q ] a ⃗ ∈ R 3 , [ Q ] a ⃗ ~ = [ Q ] a ⃗ ~ [ Q ] T \Rightarrow \left[ Q \right] \vec{a}\in \mathbb{R} ^3,\widetilde{\left[ Q \right] \vec{a}}=\left[ Q \right] \tilde{\vec{a}}\left[ Q \right] ^{\mathrm{T}} ⇒[Q]a∈R3,[Q]a =[Q]a~[Q]T
R o t ( ω ⃗ A , θ ) = e ω ⃗ ~ A θ = e [ Q B A ] ω ⃗ B ~ θ = e [ Q B A ] ω ⃗ ~ B [ Q B A ] T θ = [ Q B A ] e ω ⃗ ~ B θ [ Q B A ] T ← e P A P − 1 = P e A P − 1 Rot\left( \vec{\omega}^A,\theta \right) =e^{\tilde{\vec{\omega}}^A\theta}=e^{\widetilde{\left[ Q_{\mathrm{B}}^{A} \right] \vec{\omega}^B}\theta}=e^{\left[ Q_{\mathrm{B}}^{A} \right] \tilde{\vec{\omega}}^B\left[ Q_{\mathrm{B}}^{A} \right] ^{\mathrm{T}}\theta}=\left[ Q_{\mathrm{B}}^{A} \right] e^{\tilde{\vec{\omega}}^B\theta}\left[ Q_{\mathrm{B}}^{A} \right] ^{\mathrm{T}}\gets e^{PAP^{-1}}=Pe^AP^{-1} Rot(ωA,θ)=eω~Aθ=e[QBA]ωB θ=e[QBA]ω~B[QBA]Tθ=[QBA]eω~Bθ[QBA]T←ePAP−1=PeAP−1
3. Rigid-Body Operation via Diffeential Equation
Recall: Every [ Q ] ∈ S O ( 3 ) \left[ Q \right] \in SO\left( 3 \right) [Q]∈SO(3) can be viewed as the state transition matrix associated with the rotation ODE(1). It maps the initial position to the current position(after the rotation motion)
- p ⃗ ( θ ) = R o t ( ω ⃗ , θ ) p ⃗ 0 \vec{p}\left( \theta \right) =Rot\left( \vec{\omega},\theta \right) \vec{p}_0 p(θ)=Rot(ω,θ)p0 viewed as solution to p ⃗ ˙ ( t ) = ω ⃗ ~ p ⃗ ( t ) , p ⃗ ( 0 ) = p ⃗ 0 \dot{\vec{p}}\left( t \right) =\tilde{\vec{\omega}}\vec{p}\left( t \right) ,\vec{p}\left( 0 \right) =\vec{p}_0 p˙(t)=ω~p(t),p(0)=p0 at t = θ t=\theta t=θ
- The above relation requires that the rotation axis passes through the origin.
We can obtain similar ODE characterization for [ T ] ∈ S E ( 3 ) \left[ T \right] \in SE\left( 3 \right) [T]∈SE(3) , which will lead to exponential coordinate of SE(3)
Recall : Theorem (Chasles): Every rigid body motion can be realized by a screw motion
Consider a point p p p undergoes a screw motion with screw axis S \mathcal{S} S and unit speed ( θ ˙ = 1 \dot{\theta}=1 θ˙=1). Let the cooresponding twist be V = θ ˙ S = ( ω ⃗ , v ⃗ ) \mathcal{V} =\dot{\theta}\mathcal{S} =\left( \vec{\omega},\vec{v} \right) V=θ˙S=(ω,v) . The motion can be described be the following ODE.
p ⃗ ˙ ( t ) = ω ⃗ × p ⃗ ( t ) + v ⃗ ⇒ [ p ⃗ ˙ ( t ) 0 ] = [ ω ⃗ ~ v ⃗ 0 0 ] [ p ⃗ ( t ) 1 ] \dot{\vec{p}}\left( t \right) =\vec{\omega}\times \vec{p}\left( t \right) +\vec{v}\Rightarrow \left[ \begin{array}{c} \dot{\vec{p}}\left( t \right)\\ 0\\ \end{array} \right] =\left[ \begin{matrix} \tilde{\vec{\omega}}& \vec{v}\\ 0& 0\\ \end{matrix} \right] \left[ \begin{array}{c} \vec{p}\left( t \right)\\ 1\\ \end{array} \right] p˙(t)=ω×p(t)+v⇒[p˙(t)0]=[ω~0v0][p(t)1]
Solution in homogeneous coordinate is :
[ p ⃗ ( t ) 1 ] = exp ( [ ω ⃗ ~ v ⃗ 0 0 ] t ) [ p ⃗ ( 0 ) 1 ] \left[ \begin{array}{c} \vec{p}\left( t \right)\\ 1\\ \end{array} \right] =\exp \left( \left[ \begin{matrix} \tilde{\vec{\omega}}& \vec{v}\\ 0& 0\\ \end{matrix} \right] t \right) \left[ \begin{array}{c} \vec{p}\left( 0 \right)\\ 1\\ \end{array} \right] [p(t)1]=exp([ω~0v0]t)[p(0)1]
3.1 SE(3)
For any twist V = ( ω ⃗ , v ⃗ ) \mathcal{V} =\left( \vec{\omega},\vec{v} \right) V=(ω,v), let [ V ] \left[ \mathcal{V} \right] [V] be its matrix representation of twist V \mathcal{V} V
[ V ] = [ ω ⃗ ~ v ⃗ 0 0 ] ∈ R 4 × 4 \left[ \mathcal{V} \right] =\left[ \begin{matrix} \tilde{\vec{\omega}}& \vec{v}\\ 0& 0\\ \end{matrix} \right] \in \mathbb{R} ^{4\times 4} [V]=[ω~0v0]∈R4×4
-
The abve definition also applies to a screw axis S = ( ω ⃗ , v ⃗ ) , [ S ] = [ ω ⃗ ~ v ⃗ 0 0 ] \mathcal{S} =\left( \vec{\omega},\vec{v} \right) ,\left[ \mathcal{S} \right] =\left[ \begin{matrix} \tilde{\vec{\omega}}& \vec{v}\\ 0& 0\\ \end{matrix} \right] S=(ω,v),[S]=[ω~0v0]
-
With this notation, the solution is [ p ⃗ ( t ) 1 ] = e [ S ] t [ p ⃗ ( 0 ) 1 ] \left[ \begin{array}{c} \vec{p}\left( t \right)\\ 1\\ \end{array} \right] =e^{\left[ \mathcal{S} \right] t}\left[ \begin{array}{c} \vec{p}\left( 0 \right)\\ 1\\ \end{array} \right] [p(t)1]=e[S]t[p(0)1]
-
Fact: e [ S ] t ∈ S E ( 3 ) e^{\left[ \mathcal{S} \right] t}\in SE\left( 3 \right) e[S]t∈SE(3) is always a valid homogeneous transformation matrix.
[ T ] = e [ S ] t = [ [ Q ] R ⃗ 0 1 ] \left[ T \right] =e^{\left[ \mathcal{S} \right] t}=\left[ \begin{matrix} \left[ Q \right]& \vec{R}\\ 0& 1\\ \end{matrix} \right] [T]=e[S]t=[[Q]0R1] -
Fact: Any T ∈ S E ( 3 ) T\in SE\left( 3 \right) T∈SE(3) can be written as [ T ] = e [ S ] t \left[ T \right] =e^{\left[ \mathcal{S} \right] t} [T]=e[S]t, i.e. , it can be viewed as an operator that moves a point/frame along the screw axis S \mathcal{S} S at unit speed for time t t t
3.2 se(3)
∀ ω ⃗ ∈ R 3 → ω ⃗ ~ ∈ s o ( 3 ) → e ω ⃗ ~ θ ∈ S O ( 3 ) ∀ S ∈ R 6 → [ S ] ∣ 4 × 4 = [ ω ⃗ ~ v ⃗ 0 0 ] ∈ s e ( 3 ) → e [ S ] θ ∈ S E ( 3 ) \forall \vec{\omega}\in \mathbb{R} ^3\rightarrow \tilde{\vec{\omega}}\in so\left( 3 \right) \rightarrow e^{\tilde{\vec{\omega}}\theta}\in SO\left( 3 \right) \\ \forall \mathcal{S} \in \mathbb{R} ^6\rightarrow \left. \left[ \mathcal{S} \right] \right|_{4\times 4}=\left[ \begin{matrix} \tilde{\vec{\omega}}& \vec{v}\\ 0& 0\\ \end{matrix} \right] \in se\left( 3 \right) \rightarrow e^{\left[ \mathcal{S} \right] \theta}\in SE\left( 3 \right) ∀ω∈R3→ω~∈so(3)→eω~θ∈SO(3)∀S∈R6→[S]∣4×4=[ω~0v0]∈se(3)→e[S]θ∈SE(3)
Similar to s o ( 3 ) so\left( 3 \right) so(3) , we can define s e ( 3 ) se\left( 3 \right) se(3) :
s e ( 3 ) = { ( ω ⃗ ~ , v ⃗ ) , ω ⃗ ~ ∈ s o ( 3 ) , v ⃗ ∈ R 3 } se\left( 3 \right) =\left\{ \left( \tilde{\vec{\omega}},\vec{v} \right) ,\tilde{\vec{\omega}}\in so\left( 3 \right) ,\vec{v}\in \mathbb{R} ^3 \right\} se(3)={(ω~,v),ω~∈so(3),v∈R3}
- s e ( 3 ) se\left( 3 \right) se(3) contains all matrix representation of twists or equivalently all twists.
- In some references, [ V ] \left[ \mathcal{V} \right] [V] is called a twist
- Sometimes, we may abuse notation by writing V ∈ s e ( 3 ) \mathcal{V} \in se\left( 3 \right) V∈se(3)
4. Homogeneous Transformation Matrix as Rigid-Body Operator
-
ODE for rigid motion under V = ( ω ⃗ , v ⃗ ) \mathcal{V} =\left( \vec{\omega},\vec{v} \right) V=(ω,v)
p ⃗ ˙ = v ⃗ + ω ⃗ × p ⃗ ⇒ [ p ⃗ ˙ 0 ] = [ ω ⃗ ~ v ⃗ 0 0 ] [ p ⃗ 1 ] ⇒ [ p ⃗ ˙ 0 ] = e [ V ] t [ p ⃗ 1 ] \dot{\vec{p}}=\vec{v}+\vec{\omega}\times \vec{p}\Rightarrow \left[ \begin{array}{c} \dot{\vec{p}}\\ 0\\ \end{array} \right] =\left[ \begin{matrix} \tilde{\vec{\omega}}& \vec{v}\\ 0& 0\\ \end{matrix} \right] \left[ \begin{array}{c} \vec{p}\\ 1\\ \end{array} \right] \Rightarrow \left[ \begin{array}{c} \dot{\vec{p}}\\ 0\\ \end{array} \right] =e^{\left[ \mathcal{V} \right] t}\left[ \begin{array}{c} \vec{p}\\ 1\\ \end{array} \right] p˙=v+ω×p⇒[p˙0]=[ω~0v0][p1]⇒[p˙0]=e[V]t[p1] -
Consider “unit velocity” V = S \mathcal{V} =\mathcal{S} V=S, then time t t t means degree
if not unit speed : V = θ ˙ S \mathcal{V} =\dot{\theta}\mathcal{S} V=θ˙S -
[ p ⃗ ′ 1 ] = [ T ] [ p ⃗ 1 ] \left[ \begin{array}{c} \vec{p}^{\prime}\\ 1\\ \end{array} \right] =\left[ T \right] \left[ \begin{array}{c} \vec{p}\\ 1\\ \end{array} \right] [p′1]=[T][p1] : “rotate” p ⃗ \vec{p} p about screw axis S \mathcal{S} S by θ \theta θ degree
[ T ] = e [ S ] θ \left[ T \right] =e^{\left[ \mathcal{S} \right] \theta} [T]=e[S]θ, two points : [ p ⃗ 1 ] → [ p ⃗ ′ 1 ] \left[ \begin{array}{c} \vec{p}\\ 1\\ \end{array} \right] \rightarrow \left[ \begin{array}{c} \vec{p}^{\prime}\\ 1\\ \end{array} \right] [p1]→[p′1] , more precisely : [ p ⃗ O ′ 1 ] = [ T O ] [ p ⃗ O 1 ] \left[ \begin{array}{c} {\vec{p}^O}^{\prime}\\ 1\\ \end{array} \right] =\left[ T^O \right] \left[ \begin{array}{c} \vec{p}^O\\ 1\\ \end{array} \right] [pO′1]=[TO][pO1]
For [ T ] ∈ S E ( 3 ) \left[ T \right] \in SE\left( 3 \right) [T]∈SE(3) config representative [ T B A ] \left[ T_{\mathrm{B}}^{A} \right] [TBA] : config of { B } \left\{ B \right\} {B} relative to { A } \left\{ A \right\} {A} —— [ p ⃗ A 1 ] = [ T B A ] [ p ⃗ B 1 ] \left[ \begin{array}{c} \vec{p}^A\\ 1\\ \end{array} \right] =\left[ T_{\mathrm{B}}^{A} \right] \left[ \begin{array}{c} \vec{p}^B\\ 1\\ \end{array} \right] [pA1]=[TBA][pB1]——same physical point but two different frames -
[ T ] [ T A ] \left[ T \right] \left[ T_A \right] [T][TA] : “rotate” { A } \left\{ A \right\} {A}-frame about S \mathcal{S} S by θ \theta θ degree
Rigid-Body Operator in Different Frames
Expression of [ T ] \left[ T \right] [T] in another frame (other than { O } \left\{ O \right\} {O}):
[ T O ] ↔ [ T B O ] − 1 [ T O ] [ T B O ] \left[ T^O \right] \leftrightarrow \left[ T_{\mathrm{B}}^{O} \right] ^{-1}\left[ T^O \right] \left[ T_{\mathrm{B}}^{O} \right] [TO]↔[TBO]−1[TO][TBO]
5. Rigid-Body Operation of Screw Axis
Consider an arbitrary screw axis S \mathcal{S} S , suppose the axis has gone through a rigid transformation [ T ] = ( [ Q ] , R ⃗ ) \left[ T \right] =\left( \left[ Q \right] ,\vec{R} \right) [T]=([Q],R) and the resulting new screw axis is S ′ \mathcal{S} ^{\prime} S′ , then
S ′ = [ A d T ] S \mathcal{S} ^{\prime}=\left[ Ad_T \right] \mathcal{S} S′=[AdT]S
Let’s work an arbitrary frame { A } \left\{ A \right\} {A} (rigidly attached to the screw axis)
Let { B } \left\{ B \right\} {B} be the frame obtained be apply [ T ] \left[ T \right] [T] operation
the coordinate of S \mathcal{S} S in { A } \left\{ A \right\} {A} is the same as the coordinate of S ′ \mathcal{S} ^{\prime} S′ in { B } \left\{ B \right\} {B} : S A = S ′ B \mathcal{S} ^A={\mathcal{S} ^{\prime}}^B SA=S′B
We also know [ T B ] = [ T ] [ T A ] , [ T ] = [ T B A ] \left[ T_B \right] =\left[ T \right] \left[ T_{\mathrm{A}} \right] ,\left[ T \right] =\left[ T_{\mathrm{B}}^{A} \right] [TB]=[T][TA],[T]=[TBA]
Multiply [ X B A ] \left[ X_{\mathrm{B}}^{A} \right] [XBA] : ⇒ [ X B A ] S A = [ X B A ] S ′ B = S ′ A ⇒ S ′ A = [ X B A ] S A \Rightarrow \left[ X_{\mathrm{B}}^{A} \right] \mathcal{S} ^A=\left[ X_{\mathrm{B}}^{A} \right] {\mathcal{S} ^{\prime}}^B={\mathcal{S} ^{\prime}}^A\Rightarrow {\mathcal{S} ^{\prime}}^A=\left[ X_{\mathrm{B}}^{A} \right] \mathcal{S} ^A ⇒[XBA]SA=[XBA]S′B=S′A⇒S′A=[XBA]SA
[ X B A ] = [ [ Q B A ] 0 R ⃗ ~ B A [ Q B A ] [ Q B A ] ] = [ A d T ] \left[ X_{\mathrm{B}}^{A} \right] =\left[ \begin{matrix} \left[ Q_{\mathrm{B}}^{A} \right]& 0\\ \tilde{\vec{R}}_{\mathrm{B}}^{A}\left[ Q_{\mathrm{B}}^{A} \right]& \left[ Q_{\mathrm{B}}^{A} \right]\\ \end{matrix} \right] =\left[ Ad_T \right] [XBA]=[[QBA]R~BA[QBA]0[QBA]]=[AdT]
1
2
3
4
5
6
7
8
9
相关文章:

[足式机器人]Part4 南科大高等机器人控制课 Ch03 Operator View of Rigid-Body Transformation
本文仅供学习使用 本文参考: B站:CLEAR_LAB 笔者带更新-运动学 课程主讲教师: Prof. Wei Zhang 南科大高等机器人控制课 Ch03 Operator View of Rigid-Body Transformation 1. Rotation Operation via Differential Equation1.1 Skew Symmetr…...

SpringBoot项目静态资源默认访问目录
SpringBoot项目:静态资源默认访问目录 参考博客:https://blog.csdn.net/weixin_43808717/article/details/118281904...

xtu oj 1255 勾股数
题目描述 勾股数是指满足a2b2c2的正整数,比如最有名的“勾三股四弦五”。 现在给你两个正整数,请问是否存在另外一个正整数,使其成为“勾股数”? 输入 第一行是一个整数K,表示样例的个数。 以后每行一个样例,为两个…...

【ArcGIS Pro微课1000例】0051:创建数据最小几何边界范围(点、线、面数据均可)
本实例为专栏系统文章:创建点数据最小几何边界(范围),配套案例数据,持续同步更新! 文章目录 一、工具介绍二、实战演练三、注意事项一、工具介绍 创建包含若干面的要素类,用以表示封闭单个输入要素或成组的输入要素指定的最小边界几何。 工具界面及参数如下所示: 核心…...

Oracle 怎樣修改DB_NAME
DBNEWID 是一个数据库实用程序,用于更改 Oracle 数据库的 DBNAME 和 DBID。可以更改 DBID 或 DBNAME 或两者。 DBNAME 是在创建数据库时指定的数据库名称,DBID 是创建数据库时分配给数据库的唯一编号。 以下步骤演示如何使用 DBNEWID 实用程序更改 Oracl…...

git标签的管理与思考
git 标签管理 git 如何打标签呢? 标签是什么? 标签 相当于一个 版本管理的一个贴纸,随时 可以通过标签 切换到 这个版本的状态 , 有人可能有疑问 git commit 就可以知道 代码的改动了, 为啥还需要标签来管理呢? …...
)
ESP32网络编程-OTA方式升级固件(基于Arduino IDE)
OTA方式升级固件(基于Arduino IDE) 文章目录 OTA方式升级固件(基于Arduino IDE)1、ESP32的OTA介绍2、OTA升级固件方式3、软件准备4、硬件准备5、代码实现ESP32吸引人的编程方式之一就是通过OTA方式升级固件。本文将详细介绍在Arduino IDE中升级固件。 1、ESP32的OTA介绍 O…...

力扣-151. 反转字符串中的单词
文章目录 看下去,你一定可以理解此题,写的简单易懂力扣题目解题思路函数构成1.反转函数2.消除掉多余空格函数 整体函数 看下去,你一定可以理解此题,写的简单易懂 力扣题目 给你一个字符串 s ,请你反转字符串中 单词 …...
VSCode Keil Assintant 联合开发STM32
文章目录 VSCodeKeil AssistantUV5🥇软件下载🥇配置环境🥇插件安装🥈C/C Extension Pack🥉C/C Extension Pack介绍🥉插件安装 🥈Keil Assistant🥉Keil Assistant介绍🥉插…...

华为交换机基本配置
一、配置时间 sys ntp-service unicast-server 192.168.1.1 ntp-service unicast-server 192.168.1.2 clock timezone UTC add 8 clock timezone CST add 08:00:00 undo ntp-service disable q手动设置一个时间 clock datetime 13:43:00 2023-10-10save ysys保存!保…...
more命令)
每天一个Linux命令 -- (7)more命令
欢迎阅读《每天一个Linux命令》系列!在本篇文章中,将介绍Linux系统下的more命令,它用于逐屏显示文件的内容。 概念 more命令是Linux系统下的文件逐屏显示命令,用于逐屏显示文件的内容。 命令操作 more命令的语法如下࿱…...

JUnit 之初体验
文章目录 1.定义2.引入1)使用 Maven 工具2)使用 Gradle 工具3)使用 Jar 包 2.样例0)前提1)测试类2)测试方法3)测试断言4)实施 总结 1.定义 JUnit 是一个流行的 Java 单元测试框架&a…...

【前端设计模式】之适配器模式
适配器模式是一种常见的设计模式,用于将一个类的接口转换成客户端所期望的另一个接口。在前端开发中,适配器模式可以帮助我们解决不同框架或库之间的兼容性问题,提高代码的复用性和可维护性。 适配器模式特性 适配器类:适配器类…...
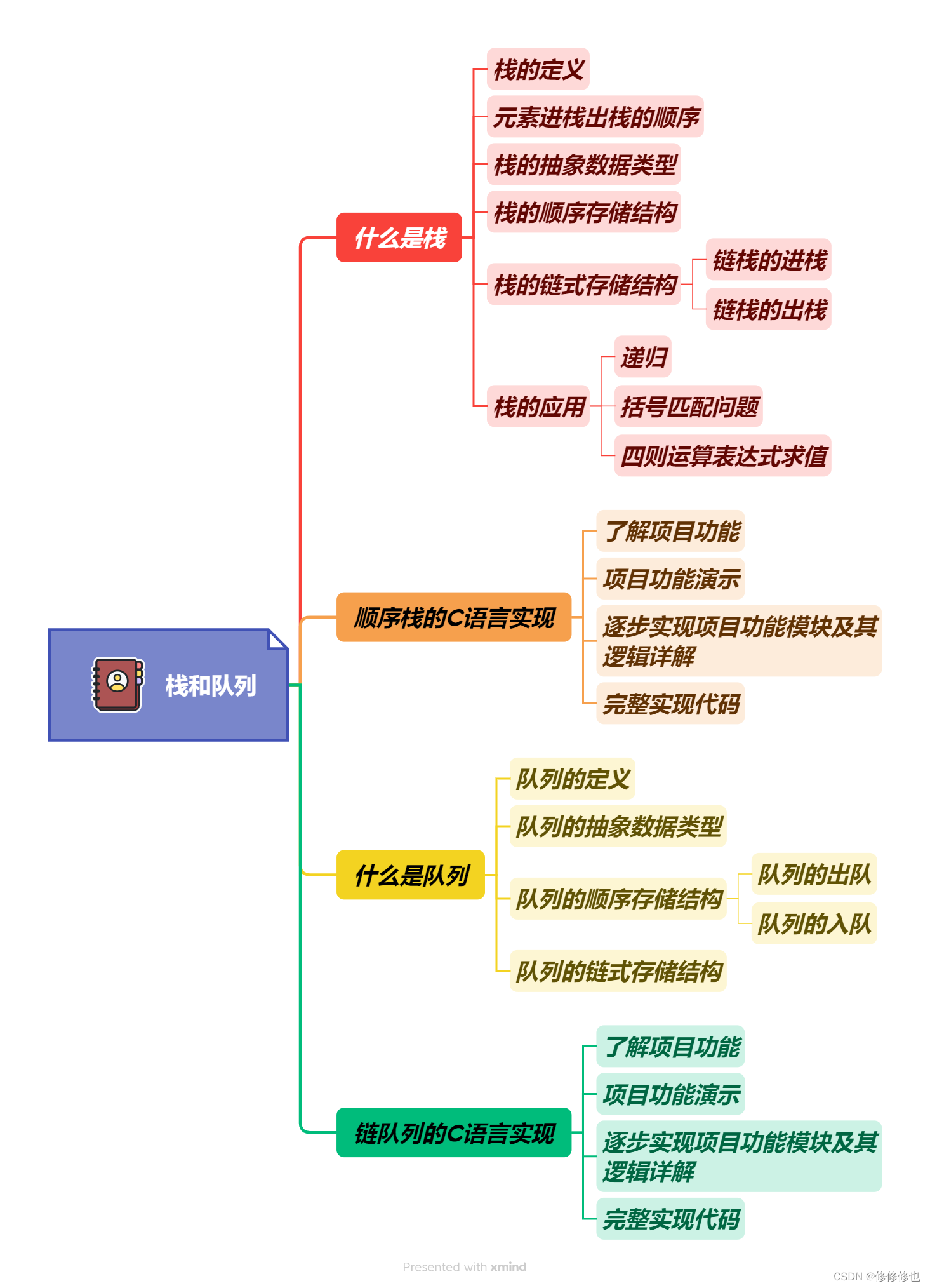
【数据结构】循环队列
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 目录 🎏队列顺序存储的不足 🎏循环队列的定义 🎏设计循环队列 结语 🎏队列顺序存储的不足 我们假设用一个可以存放为n个数据…...

Docker的资源控制
Docker的资源控制: 对容器使用宿主机的资源进行限制,Docker 通过 Cgroup 来控制容器使用的资源配额,包括 CPU 内存 磁盘i/o Docker 使用Linux自带的功能cgroup,Cgroup 是 ControlGroups 的缩写 C crontrol groups是Linux内核…...
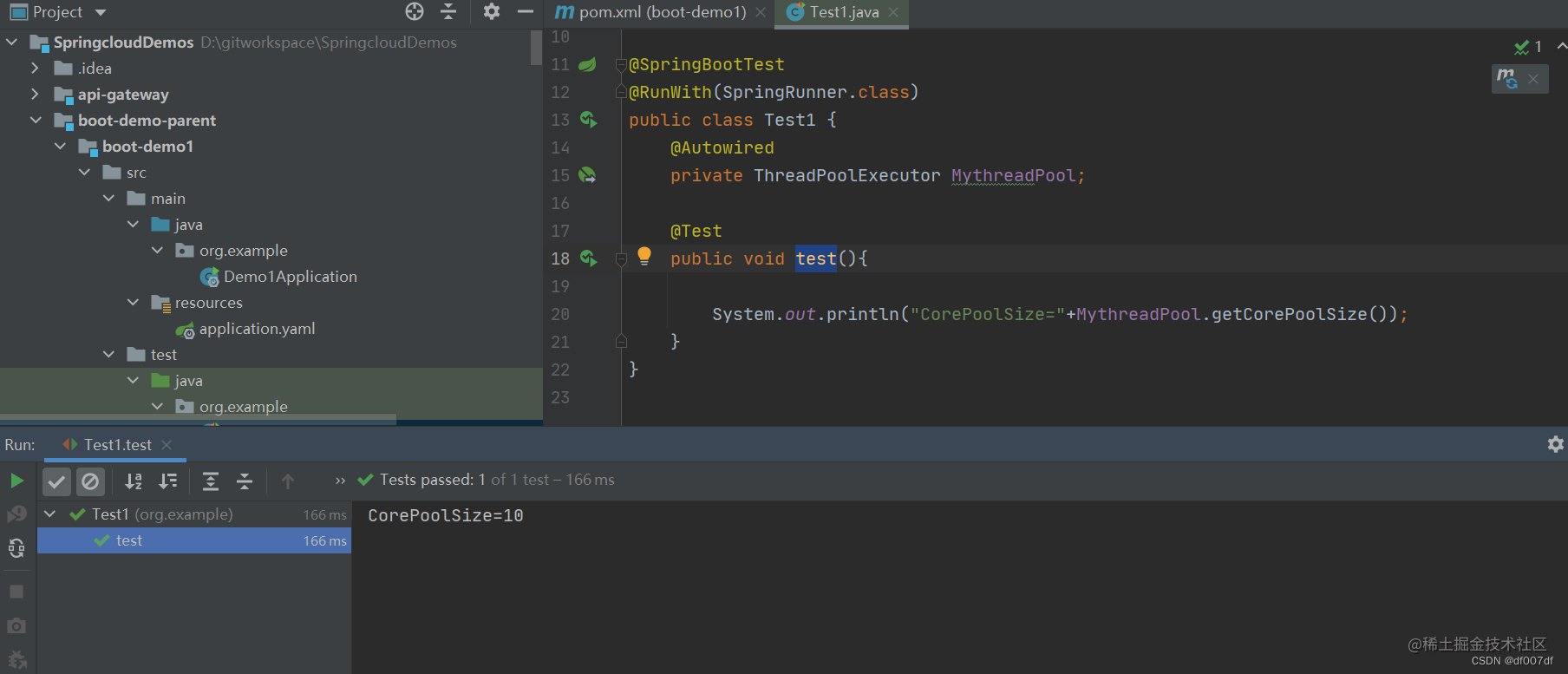
SpringBoot 自动装配原理详解
什么是 SpringBoot 自动装配? 我们现在提到自动装配的时候,一般会和 Spring Boot 联系在一起。但是,实际上 Spring Framework 早就实现了这个功能。Spring Boot 只是在其基础上,通过 SPI 的方式,做了进一步优化。 Spr…...
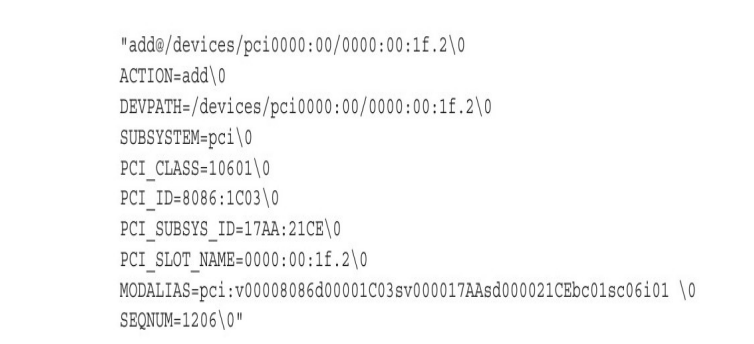
深度探索Linux操作系统 —— 构建initramfs
系列文章目录 深度探索Linux操作系统 —— 编译过程分析 深度探索Linux操作系统 —— 构建工具链 深度探索Linux操作系统 —— 构建内核 深度探索Linux操作系统 —— 构建initramfs 文章目录 系列文章目录前言一、为什么需要 initramfs二、initramfs原理探讨三、构建基本的init…...

使用cmake构建Qt6.6的qt quick项目,添加应用程序图标的方法
最近,在学习qt的过程中,遇到了一个难题,不知道如何给应用程序添加图标,按照网上的方法也没有成功,后来终于自己摸索出了一个方法。 1、准备一张图片作为图标,保存到工程目录下面,如logo.ico。 …...

VUE宝典之vue-dialog使用
文章目录 🍁vue-dialog概述🍁vue-dialog项目引入🍂安装Vue Dialog插件🍂引入Vue Dialog插件🍂引入 Vue Dialog 组件🍂在组件中使用Vue Dialog 🍁vue-dialog代码示例🍁vue-dialog父子…...

AWTK 串口屏开发(1) - Hello World
1. 功能 这个例子很简单,制作一个调节温度的界面。在这里例子中,模型(也就是数据)里只有一个温度变量: 变量名数据类型功能说明温度整数温度。范围 (0-100) 摄氏度 2. 创建项目 从模板创建项目,将 hmi/…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
