排序-选择排序与堆排序
文章目录
- 一、选择排序
- 二、堆排序
- 三、时间复杂度
- 四、稳定性
一、选择排序
思想:
将数组第一个元素作为min,然后进行遍历与其他元素对比,找到比min小的数就进行交换,直到最后一个元素就停止,然后再将第二个元素min,再遍历,以此下去直到最后一个数据
流程图:

代码实现:
//交换
void Swap(int* a,int* b) {int t = *a;*a = *b;*b = t;
}
//打印
void Print(int* arr, int n) {for (int i = 0;i < n; i++)printf("%d ", arr[i]);
}
//直接选择排序
void SelectSort(int* arr, int size) {for (int i = 0; i < size; i++){int min = i;//从第一个开始//每次从i+1的位置开始就不会影响到前面的了for (int j = i+1; j < size; j++) {//比较if (arr[min] > arr[j])min =j;//记录下标}Swap(&arr[i], &arr[min]);//交换}}
int main() {int arr[] = { 4,3,1,5,2};
SelectSort(arr, sizeof(arr) / sizeof(arr[0]));
Print(arr, sizeof(arr) / sizeof(arr[0]));return 0;
}
运行结果:
选择排序优化:
我们可以设置一个min和一个max,将小的放到左边,大的放到右边,我们再设置两个控制左右两边下标的变量p,q,当它们相遇时就结束。
流程图:

特殊情况:max的位置等于p时,我们先交换arr[p]和arr[min],但是max指向p这个位置,但是p这位置的值已经改变了,这时我们就要进行纠正,将max=min,这样才能成功找到原来在p位置的值
如:

代码实现:
//交换
void Swap(int* a,int* b) {int t = *a;*a = *b;*b = t;
}
//打印
void Print(int* arr, int n) {for (int i = 0;i < n; i++)printf("%d ", arr[i]);
}
//优化选择排序void SelectSort1(int* arr, int size) {int p = 0, q = size-1;//p指向数组开头,q指向数组最后一个位置while (p < q) {//当错过或者相遇就结束int min = p, max = p;//迭代位置for (int i = p; i <= q; i++){if (arr[min] > arr[i])//找到最小值min = i;if (arr[max] < arr[i])//找到最大值max = i;}Swap(&arr[min], &arr[p]);//交换if (max == p)//5 2 3 4 1//判断是否要纠正max = min;Swap(&arr[max], &arr[q]);//交换p++, q--;}
}
int main() {int arr[] = { 4,3,1,5,2 };SelectSort1(arr, sizeof(arr) / sizeof(arr[0]));Print(arr, sizeof(arr) / sizeof(arr[0]));return 0;
}
运行结果:
二、堆排序
堆:
结构性:用数组表示的完全二叉树;
有序性:任一结点的关键字是其子树所有结点的最大值(或最小值)
“最大堆(MaxHeap)”,也称“大顶堆”,即最大值所有父亲大于等于孩子
“最小堆(MinHeap)”,也称“小顶堆”,即最小值所有父亲小于等于孩子
小堆:堆顶数据是最小的,并且所有节点都小于左右子树
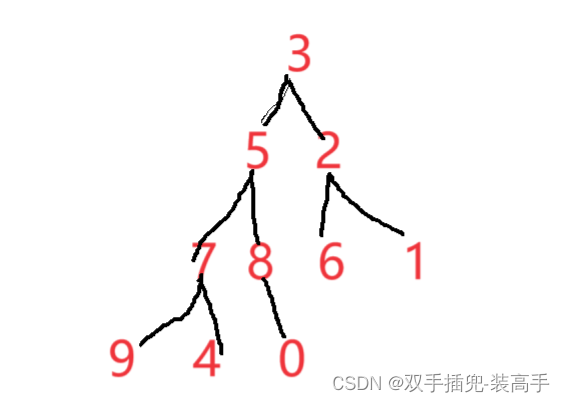
大堆:堆顶数据是最大的 ,并且所有节点都大于左右子树
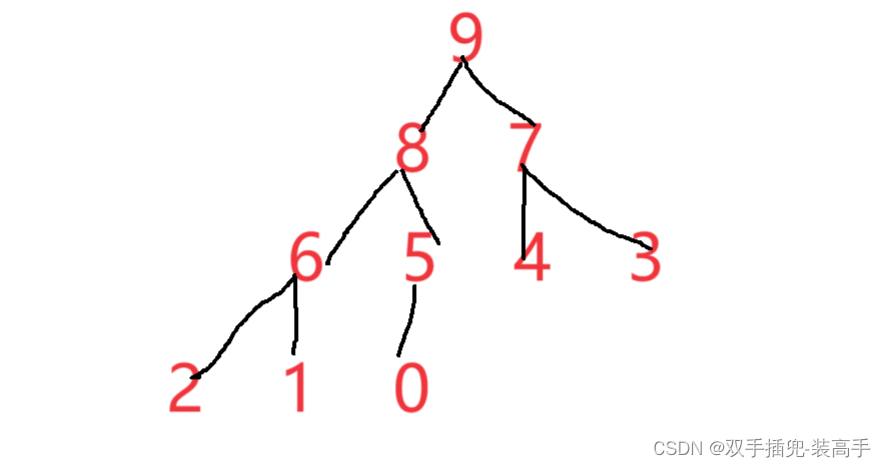
用堆来实现排序:
(1)使用向下调整算法:
前提:左右子树必须是小堆或者大堆
作用:建堆
如:
左右子树对比选择,再与根比较
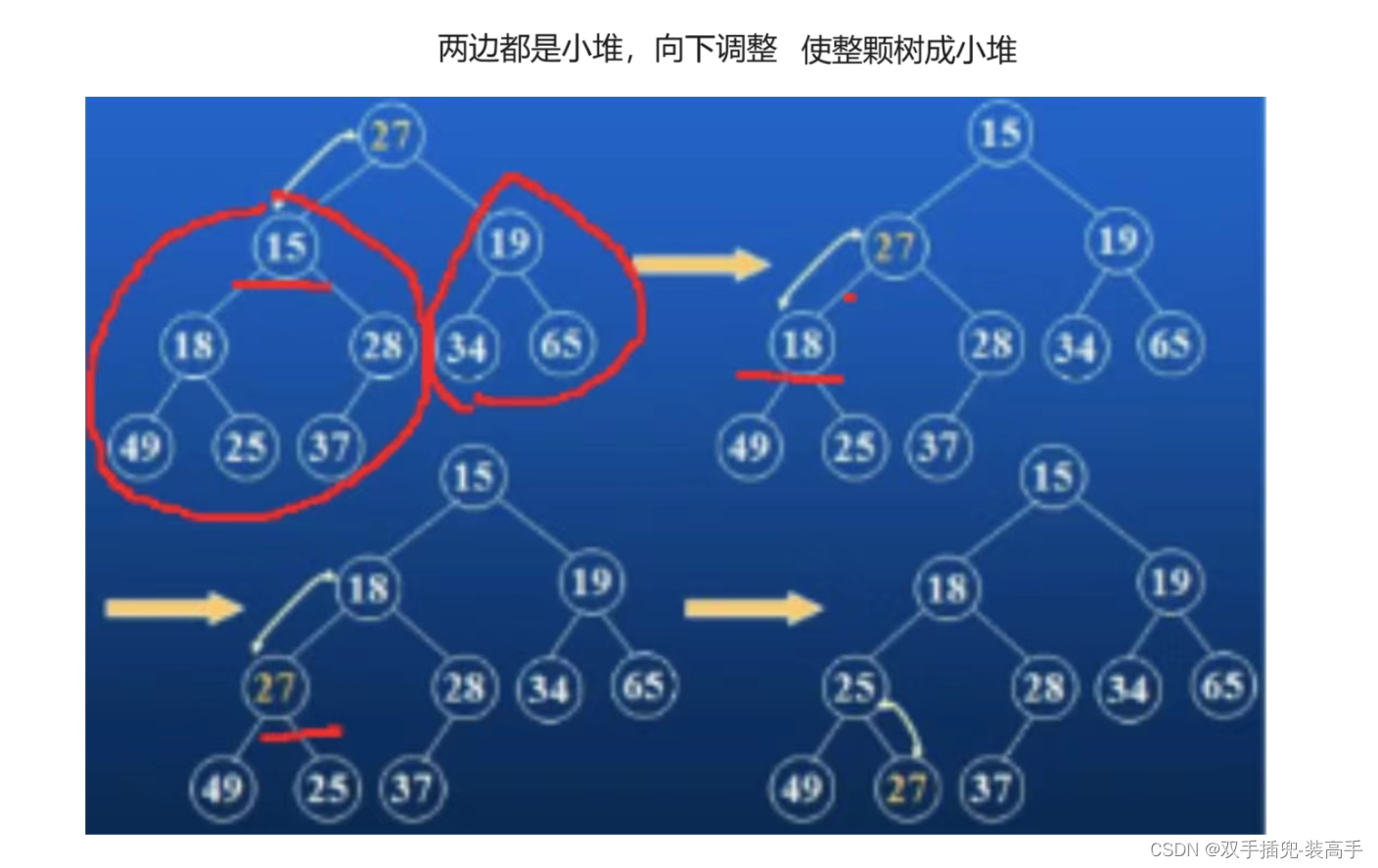
(2)建堆
当我们要实现升序时,通过向下调整法要建大堆
建的过程:因为使完全二叉树,我们可以从最后非叶点节点开始建,直到没有节点就结束。
如:
建大堆
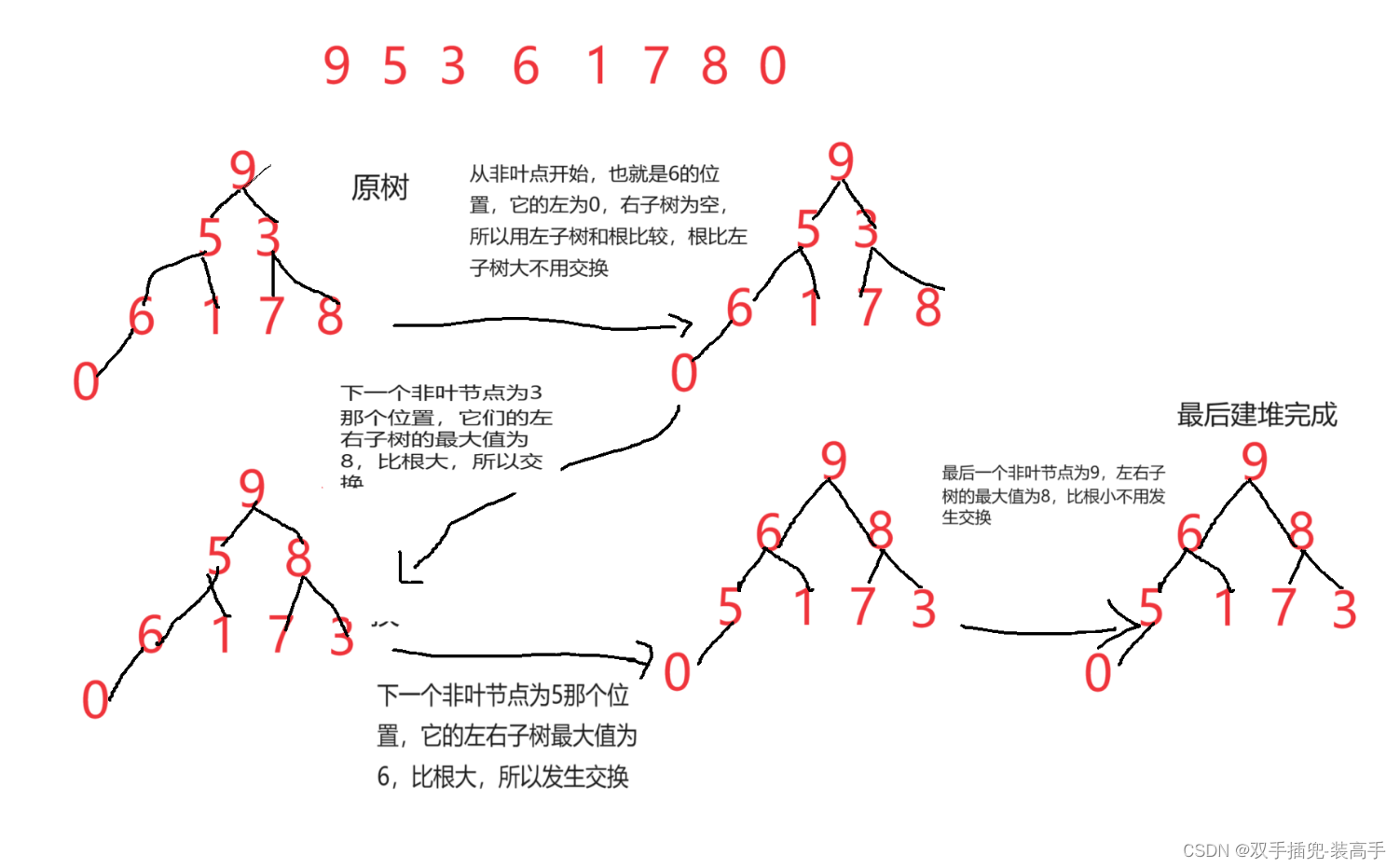
找左右子树位置:
树的左子树的下标等于根的下标*2+1,的下标等于根的下标 *2+2
建完后,我们可以将最后一个元素和第一个元素交换,然后再做向下调整即可不用重新建堆了,再让第一个元素和倒数第二个元素交换,以此类推…
为什么不建小堆呢?如果建小堆的话,用第一个根(最小值)就是数组的第一个元素了,我们不能动它,那么再让数组的第二元素重新做根,但是这样的话顺序就会被打破,又要重新建堆了,那样时间复杂度会提高(如何实现降序的话可以建小堆)
代码实现:
//交换
void Swap(int* a,int* b) {int t = *a;*a = *b;*b = t;
}
//打印
void Print(int* arr, int n) {for (int i = 0;i < n; i++)printf("%d ", arr[i]);
}
//向下调整 大堆
void AdjustDwon(int *arr,int p,int size) {int q = p;//节点位置int z = q * 2 + 1;//节点左子树,z+1就是右子树的位置了while (z<size) {//当z大于数组长度时就说明该节点不存在左右子树//判断左右子树大小,后面是判断是否有右子树if (arr[z] <arr[z + 1]&&z+1<size)z += 1;if (arr[z] > arr[q]) {//判断是否比根大Swap(&arr[z], &arr[q]);q = z;z = q * 2 + 1;//迭代}elsebreak;}
}
void HeapSort(int* arr, int size) {//建堆,size-1-1就是除2(求子树公式反过来用,最后减一是因为我们求的是下标)for (int i = (size - 1 - 1) / 2; i >= 0; i--) {AdjustDwon(arr, i, size);}int ned = size - 1;
//最后一个下标位置开始,和下标为0的元素交换,一直交换下去,并且交换一次就调整一次//当ned==1就证明排好了while (ned>0) {Swap(&arr[0], &arr[ned]);AdjustDwon(arr, 0, ned);//重新调整ned--;}
}int main() {int arr[] = { 4,3,1,5,2 };HeapSort(arr, sizeof(arr)/sizeof(arr[0]));Print(arr, sizeof(arr) / sizeof(arr[0]));
return 0}
运行结果:
三、时间复杂度
选择排序:
n-1 ,n-2…2,1
是一个等差数列求前n-1项和,粗略来算就是n^2
所以时间复杂度为O(n^2)
堆排序:
建堆:O(n)

向下调整的时间复杂度为:
假设树高为 h,树的结点为n,因为n=2^h-1,那么h=log(n-1)(以2为底)
所以为O(logn-1)
我们还要进行n次这个向下调整(当然在进行的过程中n是会变化的)
那么总的次数n+nlogn
所以时间复杂度为O(nlogn)
四、稳定性
稳定性:
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[4],且r[1]在r[4]之前,而在排序后的序列中,r[1]仍在r[4]之前,则称这种排序算法是稳定的;否则称为不稳定的。
选择排序:不稳定
如:

堆排序:不稳定
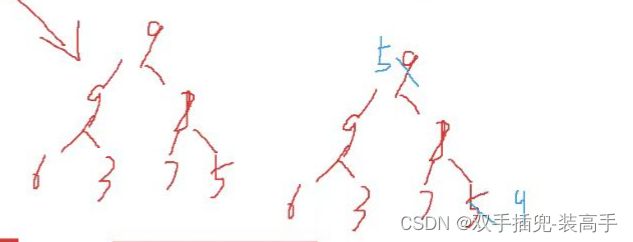
第一个9直接到最后了
以上就是我的分享了,如果有什么错误,欢迎在评论区留言。
最后,谢谢大家的观看!
相关文章:

排序-选择排序与堆排序
文章目录 一、选择排序二、堆排序三、时间复杂度四、稳定性 一、选择排序 思想: 将数组第一个元素作为min,然后进行遍历与其他元素对比,找到比min小的数就进行交换,直到最后一个元素就停止,然后再将第二个元素min&…...
d2l绘图不显示的问题
之前试了各种方法都不行 在pycharm中还是不行,但是在anaconda中的命令行是可以的 anaconda prompt conda activaye py39 #进入f盘 F: #运行文件 python F:\python_code\softmax.py...

智能优化算法应用:基于人工蜂群算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于人工蜂群算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于人工蜂群算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.人工蜂群算法4.实验参数设定5.算法结果6.…...
云原生的 CI/CD 框架tekton - Trigger(二)
上一篇为大家详细介绍了tekton - pipeline,由于里面涉及到的概念比较多,因此需要好好消化下。同样,今天在特别为大家分享下tekton - Trigger以及案例演示,希望可以给大家提供一种思路哈。 文章目录 1. Tekton Trigger2. 工作流程3…...
maven环境搭建
maven历史版本下载:https://archive.apache.org/dist/maven/ 新建系统变量编辑Path,添加bin目录mvn -v测试查看版本号conf目录下新建repository文件夹,作为本地仓库 settings.xml <?xml version"1.0" encoding"UTF-8&…...
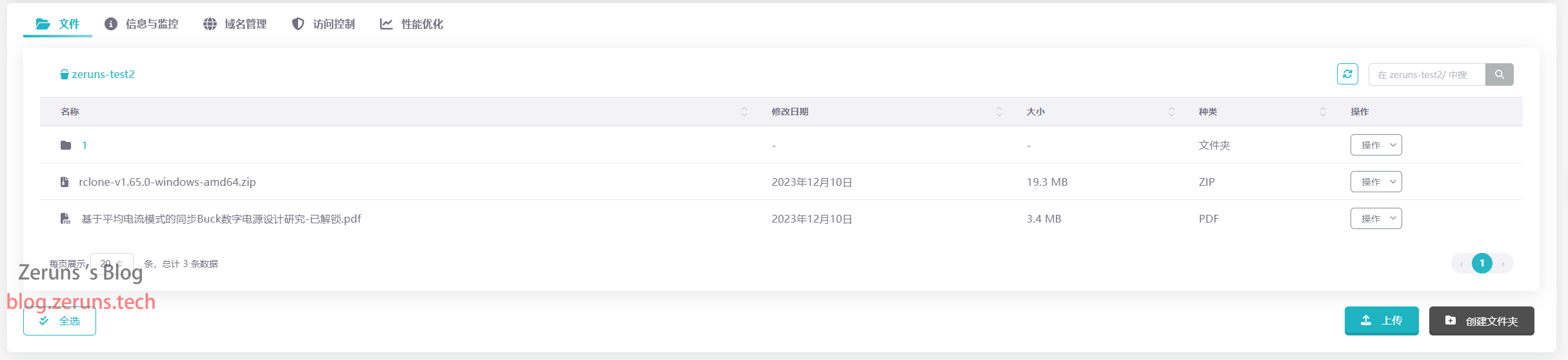
利用Rclone将阿里云对象存储迁移至雨云对象存储的教程,对象存储数据迁移教程
使用Rclone将阿里云对象存储(OSS)的文件全部迁移至雨云对象存储(ROS)的教程,其他的对象存储也可以参照本教程。 Rclone简介 Rclone 是一个用于和同步云平台同步文件和目录命令行工具。采用 Go 语言开发。 它允许在文件系统和云存储服务之间或在多个云存储服务之间…...

二叉树的前序遍历
问题描述: 给你二叉树的根节点root,返回节点值的前序遍历。 示例 1: 输入:root [1,null,2,3] 输出:[1,2,3]示例 2: 输入:root [] 输出:[]示例 3: 输入:ro…...

final的安全发布
final的安全发布 两个关键字“发布”“安全” 所谓发布通俗一点的理解就是创建一个对象,使这个对象能被当前范围之外的代码所使用 比如Object o new Object(); 然后接下来使用对象o 但是对于普通变量的创建,之前分析过,大致分为三个步骤&am…...
生成对抗网络 优化算法进化算法)
3易懂AI深度学习算法:长短期记忆网络(Long Short-Term Memory, LSTM)生成对抗网络 优化算法进化算法
继续写:https://blog.csdn.net/chenhao0568/article/details/134920391?spm1001.2014.3001.5502 1.https://blog.csdn.net/chenhao0568/article/details/134931993?spm1001.2014.3001.5502 2.https://blog.csdn.net/chenhao0568/article/details/134932800?spm10…...
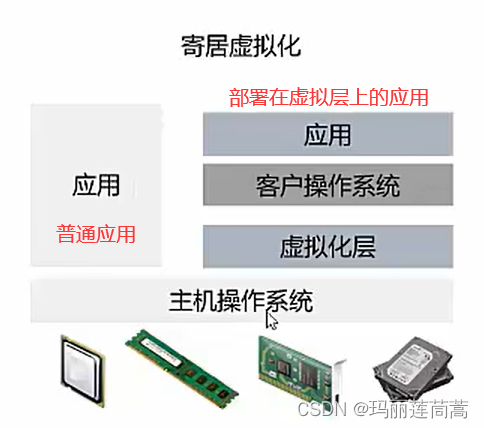
云计算 云原生
一、引言 云计算需要终端把信息上传到服务器,服务器处理后再返回给终端。在之前人手一台手机的情况下,云计算还是能handle得过来的。但是随着物联网的发展,什么东西都要联网,那数据可就多了去了,服务器处理不过来&…...

深拷贝、浅拷贝 react的“不可变值”
知识获取源–晨哥(现实中的人 嘿嘿) react中如果你想让一个值始终不变 或者说其他操作不影响该值 它只是作用初始化的时候 使用了浅拷贝–改变了初始值 会改变初始值(selectList1) 都指向同一个地址 const selectList1 { title: 大大, value: 1 };con…...

赛宁网安多领域亮相第三届网络空间内生安全发展大会
2023年12月8日,第三届网络空间内生安全发展大会在宁开幕。两院院士、杰出专家学者和知名企业家相聚南京,围绕数字经济新生态、网络安全新范式进行广泛研讨,为筑牢数字安全底座贡献智慧和力量。 大会围绕“一会、一赛、一展”举办了丰富多彩的…...
)
LintCode 123 · Word Search (DFS字符处理经典题!)
123 Word Search Algorithms Medium Description Given a 2D board and a string word, find if the string word exists in the grid. The string word can be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally o…...
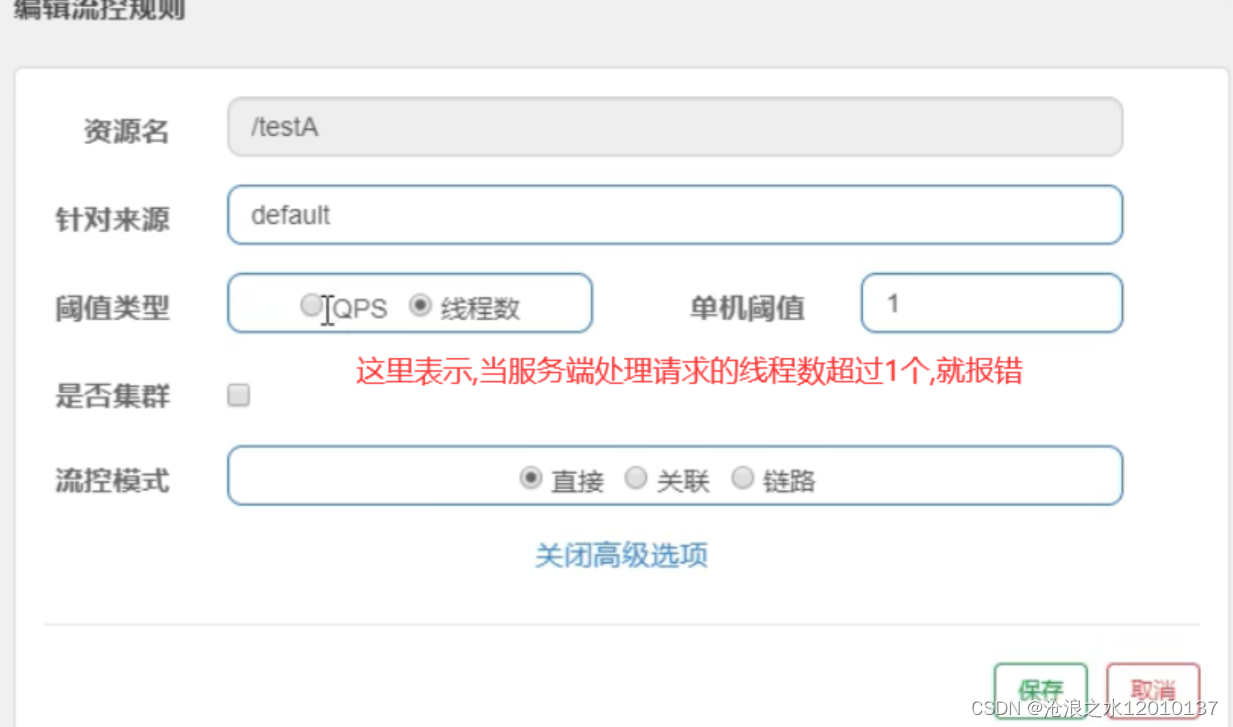
SpringCloud面试题——Sentinel
一:什么是Sentinel? Sentinel是一个面向分布式架构的轻量级服务保护框架,实现服务降级、服务熔断、服务限流等功能 二:什么是服务降级? 比如当某个服务繁忙,不能让客户端的请求一直等待,应该立刻返回给客户端一个备…...

【精选】 VulnHub (超详细解题过程)
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【python】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收藏…...
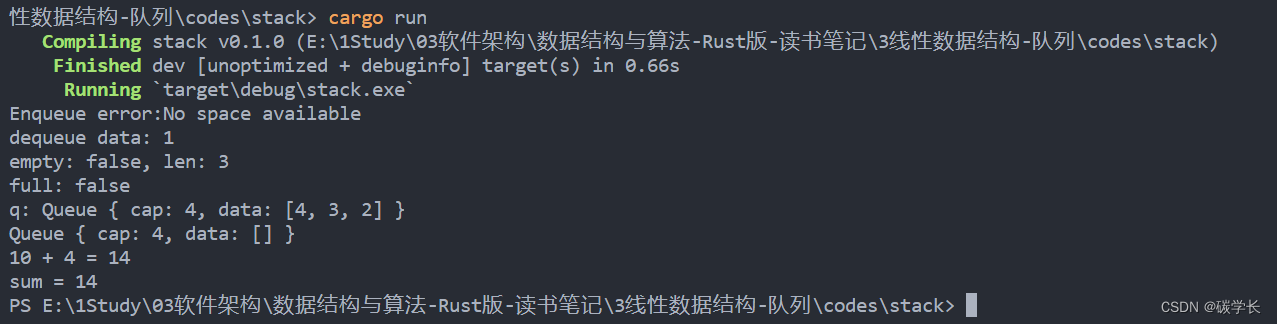
数据结构与算法-Rust 版读书笔记-2线性数据结构-队列
数据结构与算法-Rust 版读书笔记-2线性数据结构-队列 1、队列:先进先出 队列是项的有序集合,其中,添加新项的一端称为队尾,移除项的另一端称为队首。一个元素在从队尾进入队列后,就会一直向队首移动,直到…...

Android Kotlin Viewbinding封装
目录 Viewbinding配置 Activity封装 Activity使用 Fragment封装 Fragment使用 Dialog封装 Dialog使用 Viewbinding配置 android { viewBinding { enabled true } } Activity封装 import android.os.Bundle import android.view.LayoutInflater import androidx.ap…...
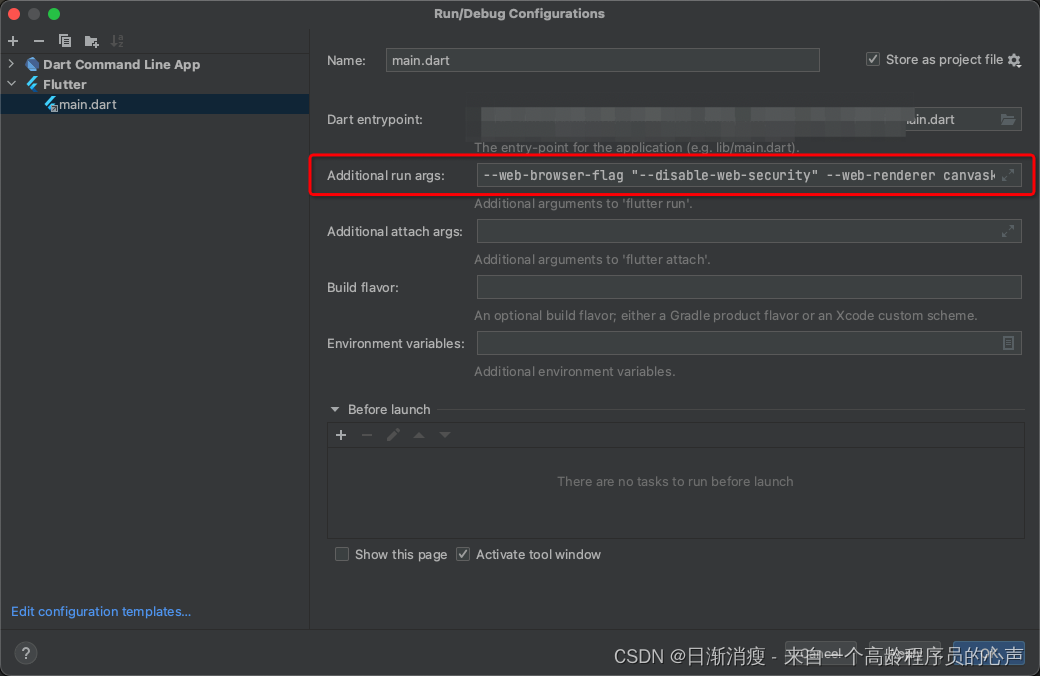
Flutter:web项目跨域问题解决
前后端解决系列 文章目录 一、Flutter web客户端解决本地环境调试跨域问题二、Flutter web客户端解决线上环境跨域问题 一、Flutter web客户端解决本地环境调试跨域问题 就一句命令【--web-browser-flag "--disable-web-security"】,用来屏蔽浏览器域名请…...
--A2L文件生成的方法)
汽车标定技术(十二)--A2L文件生成的方法
目录 1.工具生成 1.1 CANape/ASAP2 Studio 1.2 ASAP2ToolKit 1.3 Matlab/Simulink 2.手写A2L要点 3.小结 A2L文件的制作一直以来是一个很少有人关注的方向,不管是标定工程师还是Slave协议栈的开...

《PySpark大数据分析实战》-03.了解Hive
📋 博主简介 💖 作者简介:大家好,我是wux_labs。😜 热衷于各种主流技术,热爱数据科学、机器学习、云计算、人工智能。 通过了TiDB数据库专员(PCTA)、TiDB数据库专家(PCTP…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...
