FastAPI之响应模型
前言
响应模型我认为最主要的作用就是在自动化文档的显示时,可以直接给查看文档的小伙伴显示返回的数据格式。对于后端开发的伙伴来说,其编码的实际意义不大,但是为了可以不用再额外的提供文档,我们只需要添加一个 response_model=xxx,还是很爽的
示例
没有响应模型
from fastapi import FastAPI, Header
from pydantic import BaseModelapp = FastAPI()class Resp(BaseModel):code: intmsg: strdata: list@app.get("/")
async def read_root():return Resp(code=0, msg='success', data=[{"name": "Python"}, {"name": "Java"}])
效果
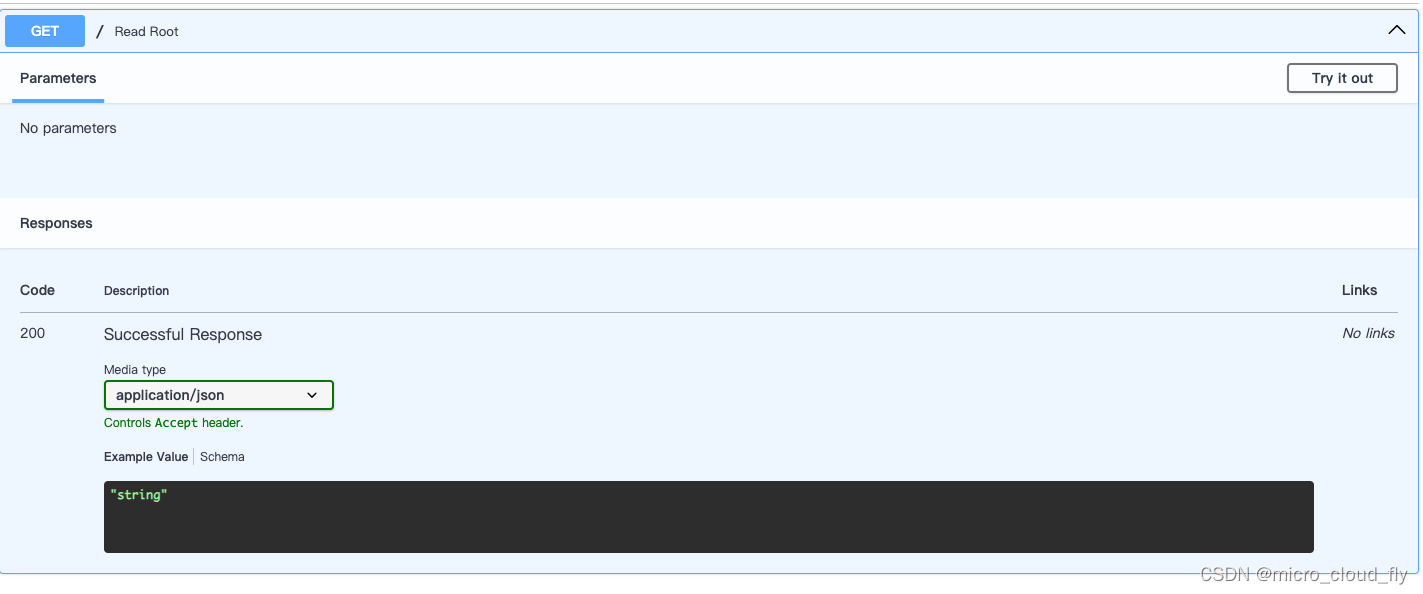
此时我们的文档只可以看到返回的是字符串,这和没写文档一样,现在尝试加上response_model
添加响应模型
from fastapi import FastAPI, Header
from pydantic import BaseModelapp = FastAPI()class User(BaseModel):id: intname: strclass Resp(BaseModel):code: intmsg: strdata: list[User]@app.get("/",response_model=Resp)
async def read_root():return Resp(code=0,msg='success',data=[User(id=1, name='test'),User(id=2, name='test2')])
打开自动化文档,显示效果如下:
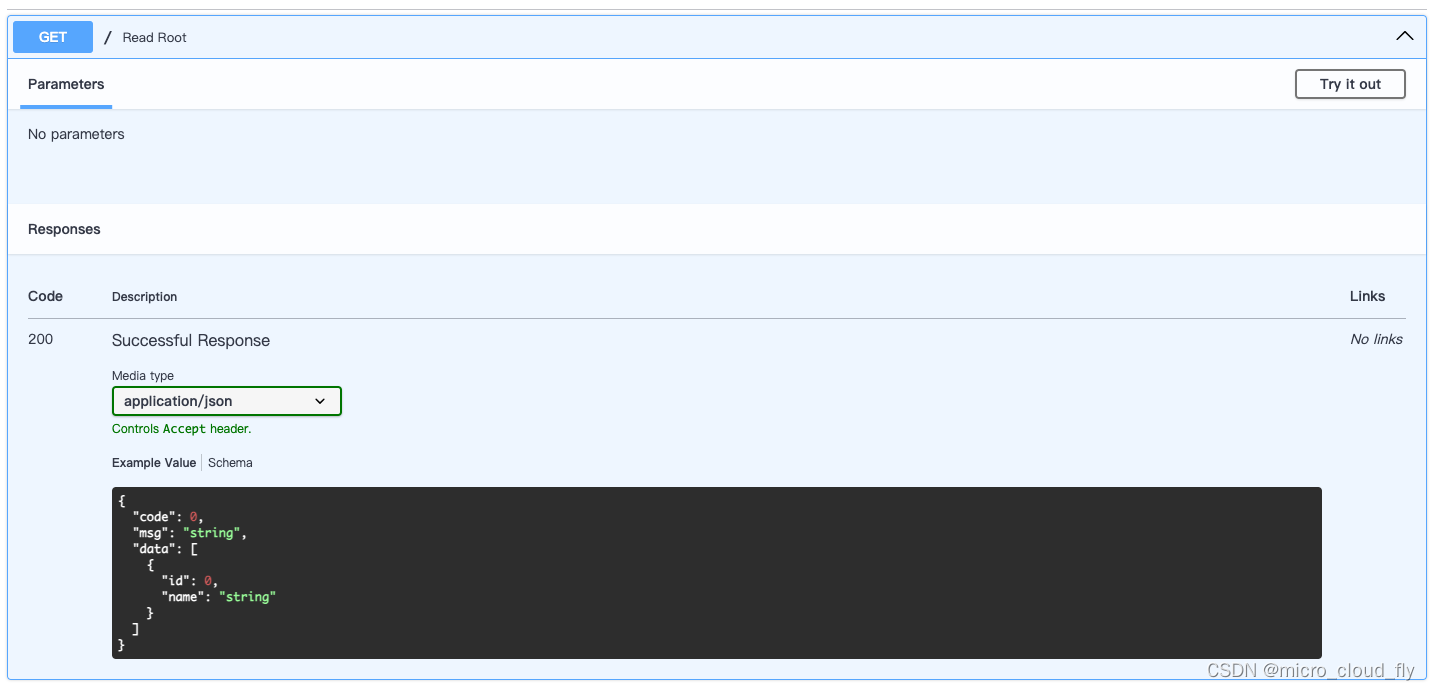
此时我们需要格外注意,我们规定了返回的是Resp模型,这个模型中有code、msg、data三个字段,如果我们返回的数据缺少了一个字段,那么,请求接口的时候,就会报错,比如我们把msg='success'注释掉,再次请求,将会有错误产生:

进阶使用:response_model_exclude_unset
如果你不想在响应模型中包括默认值未被修改的字段,你可以使用response_model_exclude_unset参数。
@app.post("/items/exclude_unset", response_model=Item, response_model_exclude_unset=True)
async def create_item_exclude_unset(item: Item):return item
在这个例子中,如果你提交了一个不包含description和tax字段的请求(因为它们有默认值且未修改),响应将不会包含这些字段。
response_model_include和response_model_exclude
response_model_include和response_model_exclude参数让你可以更精细地控制响应数据。response_model_include指定应该包含的字段,而response_model_exclude指定应该排除的字段。
只包含特定字段
@app.post("/items/include", response_model=Item, response_model_include={"name", "price"})
async def create_item_include(item: Item):return item
在这个例子中,响应只会包含name和price字段,即使其他字段在请求体中被定义。
排除特定字段
@app.post("/items/exclude", response_model=Item, response_model_exclude={"tax"})
async def create_item_exclude(item: Item):return item
在这个例子中,返回的响应将不包含tax字段。
实操演示
为了更好地理解这些概念,我们实现一个实例,其中我们创建一个简单的商品入库API,并在不同的端点展示response_model的不同用法。
from typing import Setfrom fastapi import FastAPI
from pydantic import BaseModelapp = FastAPI()class Item(BaseModel):name: strdescription: str = Noneprice: floattax: float = Nonetags: Set[str] = set()# 默认的response_model使用
@app.post("/items/", response_model=Item)
async def create_item(item: Item):return item# 排除未设置的字段
@app.post("/items/exclude_unset", response_model=Item, response_model_exclude_unset=True)
async def create_item_exclude_unset(item: Item):# 模拟item创建return item# 只包含特定字段
@app.post("/items/include_only", response_model=Item, response_model_include=["name", "price"])
async def create_item_include_only(item: Item):# 模拟item创建return item# 排除特定字段
@app.post("/items/exclude_some", response_model=Item, response_model_exclude=["tax"])
async def create_item_exclude_some(item: Item):# 模拟item创建return item
当你运行这个FastAPI应用并向这些端点发送请求时,你应该会注意到,每个端点都根据设定的参数,返回不同结构的JSON响应。
记得要调试和测试每个端点,确保它的行为符合预期,这样你就能更好地理解response_model的这些高级特性如何帮助你控制API的响应格式。
结论
response_model和其他相关参数提供了强大的方式来控制你的API响应。通过选择性地包括、排除或者隐藏响应数据的特定字段,你可以创建更加灵活和高效的API端点。这些特性尤其在处理大型数据模型或希望限制客户端收到数据的场景下非常有用。通过本教程的介绍,希望你能在自己的FastAPI项目中更加自如地使用这些高级功能。
相关文章:

FastAPI之响应模型
前言 响应模型我认为最主要的作用就是在自动化文档的显示时,可以直接给查看文档的小伙伴显示返回的数据格式。对于后端开发的伙伴来说,其编码的实际意义不大,但是为了可以不用再额外的提供文档,我们只需要添加一个 response_mod…...

Python数据科学视频讲解:数据清洗、特征工程和数据可视化的注意事项
1.6 数据清洗、特征工程和数据可视化的注意事项 视频为《Python数据科学应用从入门到精通》张甜 杨维忠 清华大学出版社一书的随书赠送视频讲解1.6节内容。本书已正式出版上市,当当、京东、淘宝等平台热销中,搜索书名即可。内容涵盖数据科学应用的全流程…...
Unity优化——加速物理引擎1
大家好,这里是七七,今天开始更新物理引擎相关的优化部分了,本文介绍的是物理引擎内部工作情况。 Unity技术有两种不同的物理引擎:用于3D物理的Nvidia的PhysX和用于2D物理的开源项目Box2D。然而,Unity对它们的实现是高…...

PHP的最新版本是多少?有什么新特性?
截至日期(2022年1月),PHP的最新稳定版本是PHP 8.0。以下是PHP 8.0的一些主要新特性: JIT 编译器: 引入了即时编译(Just-In-Time,JIT)引擎,提升了PHP脚本的执行性能。 命…...
漏洞复现-云安宝-云匣子Fastjson命令执行(附漏洞检测脚本)
免责声明 文章中涉及的漏洞均已修复,敏感信息均已做打码处理,文章仅做经验分享用途,切勿当真,未授权的攻击属于非法行为!文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何直接或者间接的…...

oh-my-zsh 安装和配置
安装zsh sudo apt update sudo apt install zsh安装oh-my-zsh sh -c "$(curl -fsSL https://gitee.com/mirrors/oh-my-zsh/raw/master/tools/install.sh)"配置~/.zshrc sudo vim ~/.zshrc添加以下内容 ZSH_THEME"steeef" HISTFILE~/.zsh_history HISTS…...

LinuxBasicsForHackers笔记 -- 日志系统
日志文件存储有关操作系统和应用程序运行时发生的事件的信息,包括任何错误和安全警报。 rsyslog 日志守护进程 Linux 使用名为 syslogd 的守护进程自动记录计算机上的事件。 rsyslog 配置文件 与 Linux 中的几乎所有应用程序一样,rsyslog 由位于 /et…...

WPS Office JS宏实现批量处理Word中的标题和正文的样式
该篇讲解下word文档中的标题和正文批量修改样式,如下图: 前面一篇已讲解了WPS Office宏编辑器操作方法,这里不细讲了,如有不清楚可以查看该篇:https://blog.csdn.net/jiciqiang/article/details/134653657?spm1001.20…...

论文怎么改才能降低重复率
一、引言:智能工具助力,轻松降低论文重复率 论文的重复率是学术写作中的重要问题,如何有效降低重复率成为了许多研究者的关注焦点。如今,智能工具的发展为我们提供了更多选择。本文将介绍几种实用的智能工具,包括快码…...

【从零开始学习JVM | 第六篇】快速了解 直接内存
前言: 当谈及Java虚拟机(JVM)的内存管理时,我们通常会想到堆内存和栈内存。然而,还有一种被称为"直接内存"的特殊内存区域,它在Java应用程序中起着重要的作用。直接内存提供了一种与Java堆内存和…...
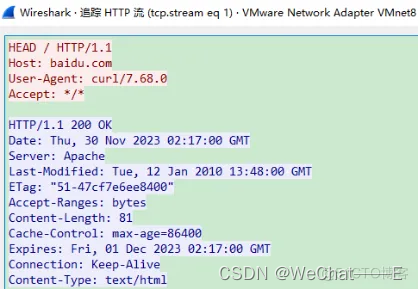
Wireshark中的http协议包分析
Wireshark可以跟踪网络协议的通讯过程,本节通过http协议,在了解Wireshark使用的基础上,重温http协议的通讯过程。 TCP(Transmission Control Protocol,传输控制协议)是一种面向连接的、可靠的、基于 字节流…...
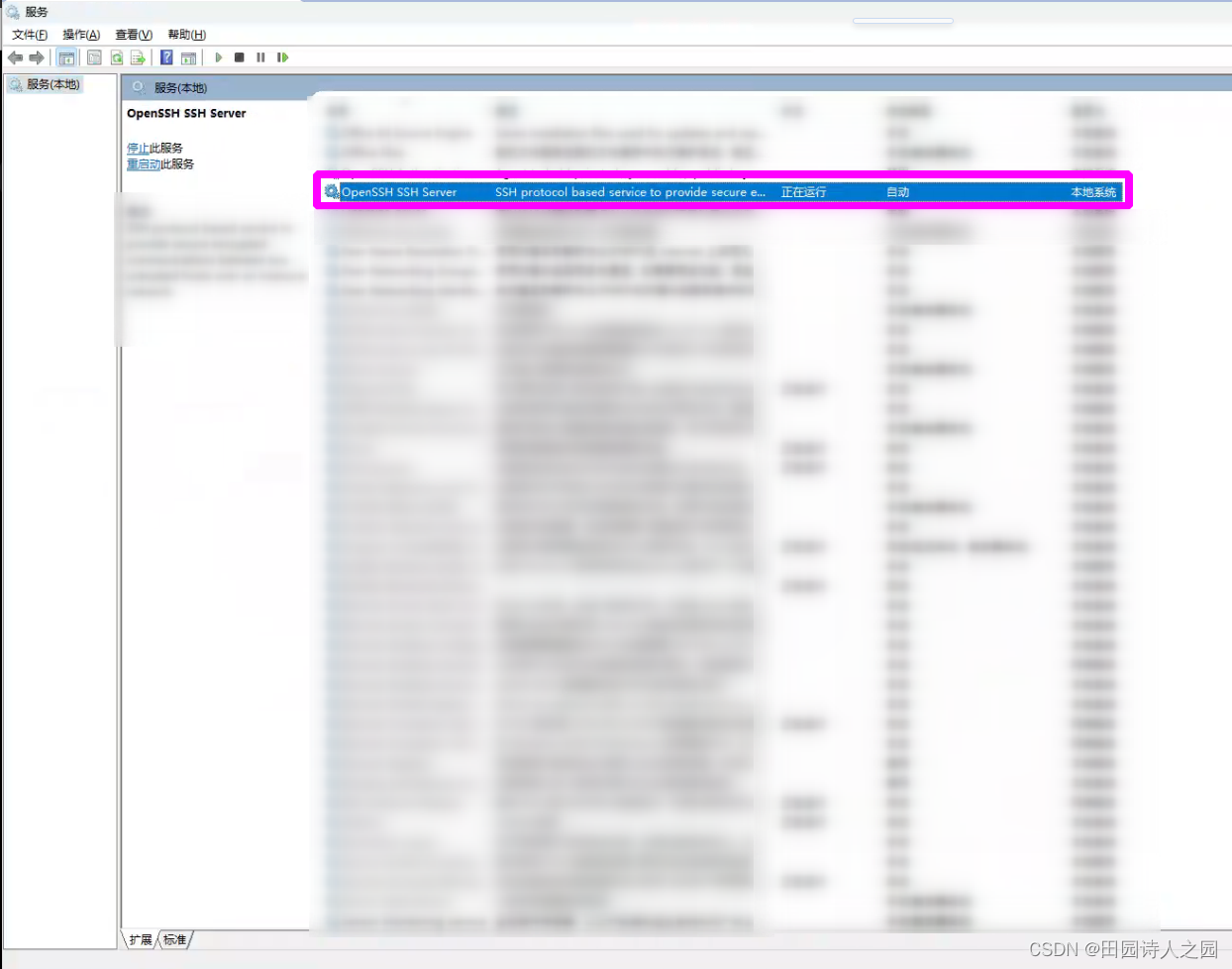
ubuntu如何远程ssh登录Windows环境并执行测试命令
ubuntu如何远程ssh登录Windows环境并执行测试命令 1 paramiko模块简介1.1 安装paramiko1.2 paramiko基本用法1.2.1 创建SSHClient实例1.2.2 设置主机密钥策略1.2.3 连接SSH服务器1.2.4 执行命令1.2.5 关闭SSH连接1.2.6 异常处理 2 windows的配置2.1 启动OpenSSH服务2.2 配置防火…...

人工智能应用专栏----专栏介绍
文章目录 本专栏主要记录人工智能的应用方面的内容,包括chatGPT、AI绘图等等; 订阅后可私聊我获取 《从零注册并登录使用ChatGPT》 《从零开始使用chatGPT的API;通过chatgpt-next-web部署自己chatGPT web网页;无需翻墙,…...
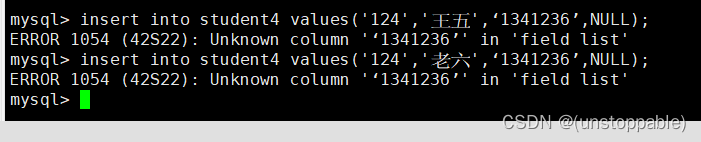
【lesson11】表的约束(4)
文章目录 表的约束的介绍唯一键约束测试建表插入测试建表插入测试建表插入测试修改表插入测试 表的约束的介绍 真正约束字段的是数据类型,但是数据类型约束很单一,需要有一些额外的约束,更好的保证数据的合法性,从业务逻辑角度保…...
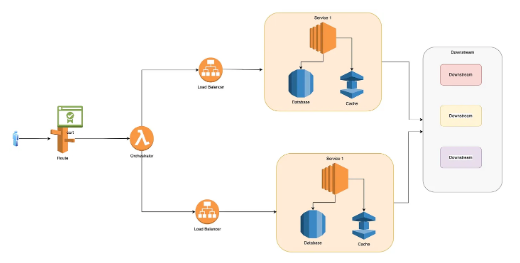
将单体应用程序迁移到微服务
多年来,我处理过多个单体应用,并将其中一些迁移到了微服务架构。我打算写下我所学到的东西以及我从经验中用到的策略,以实现成功的迁移。在这篇文章中,我将以AWS为例,但基本原则保持不变,可用于任何类型的基…...
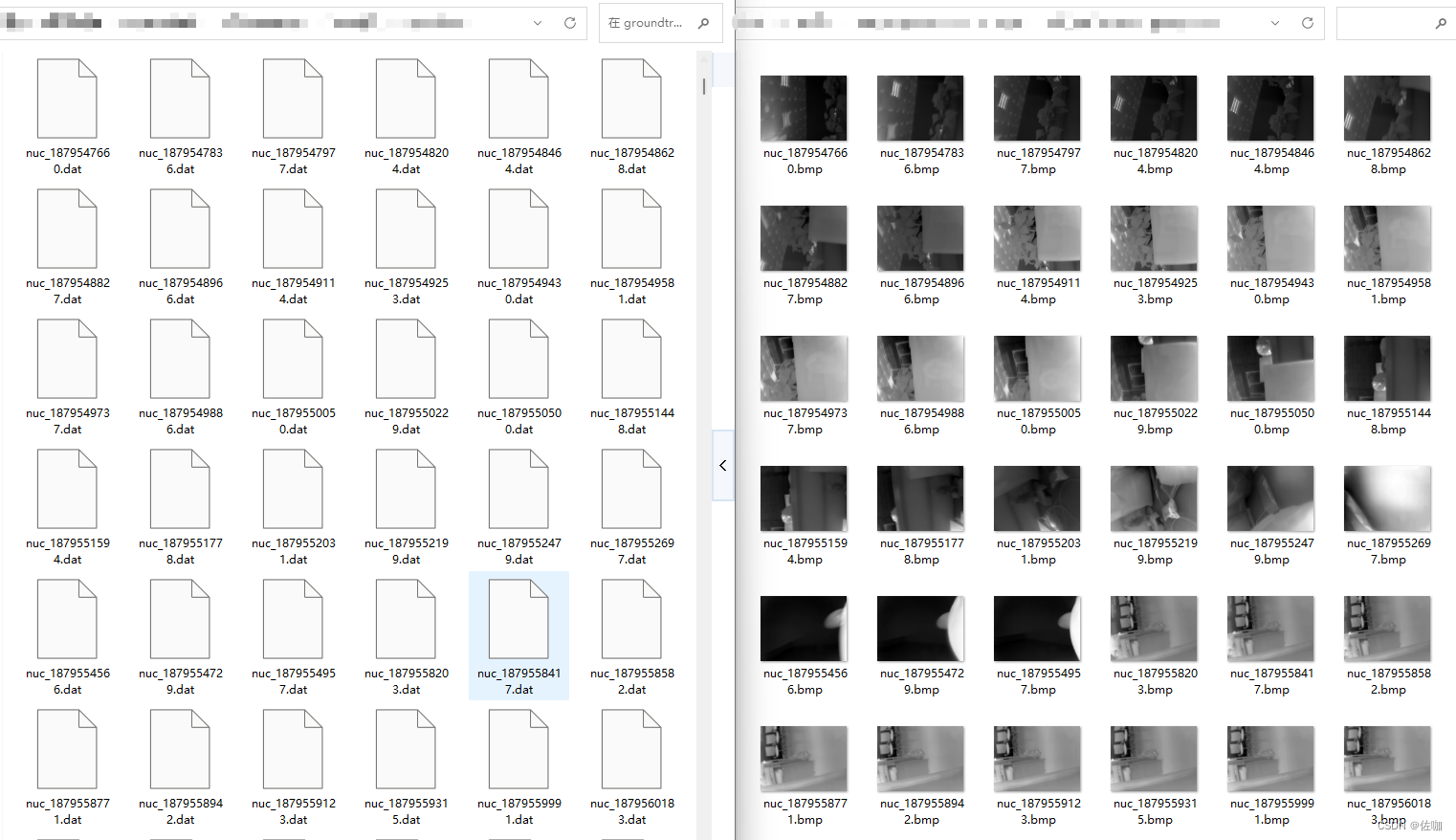
Python读取.dat格式数据并转为.png,.jpg,.bmp等可视化格式(附代码)
.dat文件的命名规则没有统一的规定,但通常以.dat为扩展名。 目录 一、 .dat格式数据1.1 .dat数据用途1.2 常见的.dat文件格式1.3 .dat文件示例 二、读取.dat格式数据2.1 单个.dat文件读取并转换2.1.1 代码2.1.2 查看数据2.1.3 输出查看8Bit图片 2.2 批量.dat文件读取…...
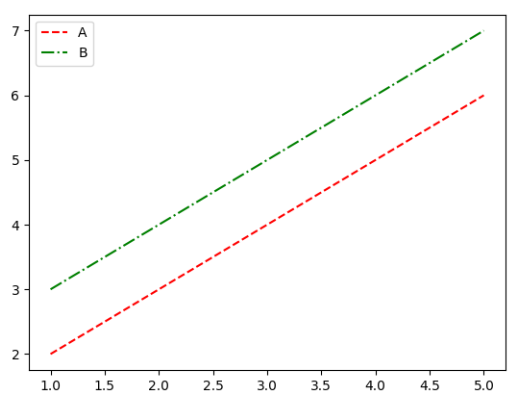
matplotlib 默认属性和绘图风格
matplotlib 默认属性 一、绘图风格1. 绘制叠加折线图2. Solarize_Light23. _classic_test_patch4. _mpl-gallery5. _mpl-gallery-nogrid6. bmh7. classic8. fivethirtyeight9. ggplot10. grayscale11. seaborn12. seaborn-bright13. seaborn-colorblind14. seaborn-dark15. sea…...

ip地址怎么转化为十进制
IP地址是在计算机网络中广泛使用的一种标识符,它用于唯一地标识网络上的设备。在网络通信过程中,IP地址扮演着非常重要的角色。但是,对于一些非专业人士来说,IP地址可能是一个陌生的概念。为了更好地理解IP地址,本文…...

【Spring进阶系列丨第五篇】详解Spring中的依赖注入
文章目录 一、说明二、构造函数注入2.1、方式一【index索引方式】2.1.1、定义Bean2.1.2、主配置文件中配置Bean2.1.3、测试 2.2、方式二【indextype组合方式】2.2.1、定义Bean2.2.2、主配置文件配置Bean2.2.3、测试2.2.4、解决方案 2.3、方式三【name方式】2.3.1、定义Bean2.3.…...

DAP数据集成与算法模型如何结合使用
企业信息化建设会越来越完善,越来越体系化,当今数据时代背景下更加强调、重视数据的价值,以数据说话,通过数据为企业提升渠道转化率、改善企业产品、实现精准运营,为企业打造自助模式的数据分析成果,以数据…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
