直接插入排序与希尔排序
目录
前言
插入排序
直接插入排序
时空复杂度
直接插入排序的特性
希尔排序(缩小增量排序)
预排序
顺序排序
多组并排
小总结
直接插入排序
时空复杂度
希尔排序的特性
前言
字可能有点多,但是真的理解起来真的没那么难😘
记得一定要连起来看,我把排序的实现过程拆开来讲述了😭😭😭
插入排序
基本思想:每次将一个待排序的记录按其关键字大小插入到前面已经排好的子序列,直到全部记录插入完成
分类:直接插入排序、折半插入排序(不再描述)、希尔排序
注意事项:解决排序的基本思想是先解决一次排序的内容,然后再去解决整体的排序
直接插入排序
基本思想:向有序数组中插入数据后,使数组重新有序(插入数据前数组已经有序了)
实现步骤:1、起初我们假设有序数组的范围为[0,end]([0,end]并不是整个数组的长度只是数组中有序数组的长度)end表示有序数组尾元素的下标,tmp表示有序数组尾元素的下一个元素

2、判断tmp是否小于有序数组中的下标为end的元素,如果小于则将下标为end的元素往后挪一位(后续空间足够且均为空)--end,再次将此时下标为end的元素与tmp比较,大于tmp则该元素也向后移动......

3、如果tmp大于等于下标为end的元素,那么证明它应该在当该元素的后面一位,即下标为end+1的位置,break跳出循环,然后进行赋值(a[end + 1] = tmp)
4、如果一直到最后有序数组中元素个数都大于tmp,此时end的下标会变为-1,跳出循环后将tmp的值放在有序数组的首元素位置即a[end + 1] = a[-1 + 1] = a[0]处即可(这也是为什么不在else中进行a[end+1] = tmp赋值的原因,就是为了防止有序数组全部比较完后,发现tmp需要位于有序数组首元素的位置,而此时end值变为-1,会导致跳出循环,如果这时候赋值a[-1]是非法的,倒不如和“如果中间出现了tmp大于等于下标为end的元素要跳出循环赋值的”情况放在一起)
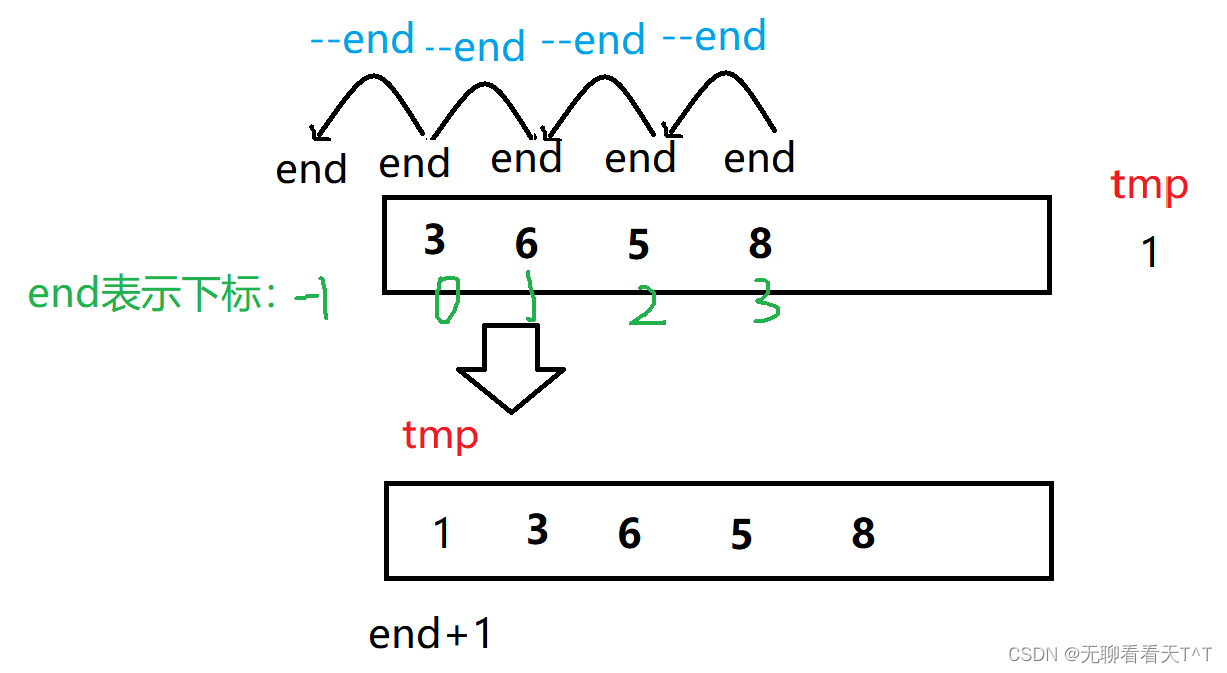
int end;
int tmp = a[end + 1];
while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else{break;}}
a[end + 1] = tmp;
5、至此我们完成了将一个数据插入有序数组的过程,那么我们该如何实现将整个无序数组通过直接插入排序变为有序呢?答:只需要一点点的改动
6、让我们为这段程序套上一层外壳:
//直接插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; ++i){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}}
这就是完整的直接插入排序了,其中InsertSort函数的两个参数int* a表示传入的无序数组,int n表示整个数组的长度,它与将一个数据插入有序数组的代码的区别在于,外套了一层for循环,以及将end赋值为i
7、for循环实现的效果是将数组中的每一个元素都遍历一遍,并进行插入数组的操作,i表示数组元素下标,初始化i为0,数组的长度为n,所以数组元素下标i应该n-1,即i < n-1(额,为什么要写小于这是一个求闭区间中数字个数的数学问题:(n-1) - (0) +(1) = n )
8、将end赋值为i,是为了配合外层的for循环,当i=0时我们将数组下标为0的元素视为一个有序数组,然后接下来就是向有序数组中插入数据然后通过直接插入排序使数组重新变得有序的过程(也就是我们第一个代码块中实现的效果)
时空复杂度
最坏时间复杂度:O(N^2)(数组完全逆序,1个无序需比较n次,n个无序需比较n^2次)
最好时间复杂度:O(N)(当个数为n的数组中只有一个数不满足有序)
空间复杂度:O(1)
直接插入排序的特性
1、元素集合越接近有序,直接插入排序算法的时间效率越高
2、它是一种稳定的排序算法
希尔排序(缩小增量排序)
基本思想:将待排序的序列分割成若干个子序列,并对这些子序列进行插入排序,每进行完一轮对子序列的插入排序,就缩小它们之间的增量,通过多次重复上述内容,最终使整个序列变的十分的趋近于一个完整的有序序列(预排序),当它们之间的间隔缩小为1时,再进行一次完整的直接插入排序即可将整个序列变为完整的有序序列(直接插入排序)
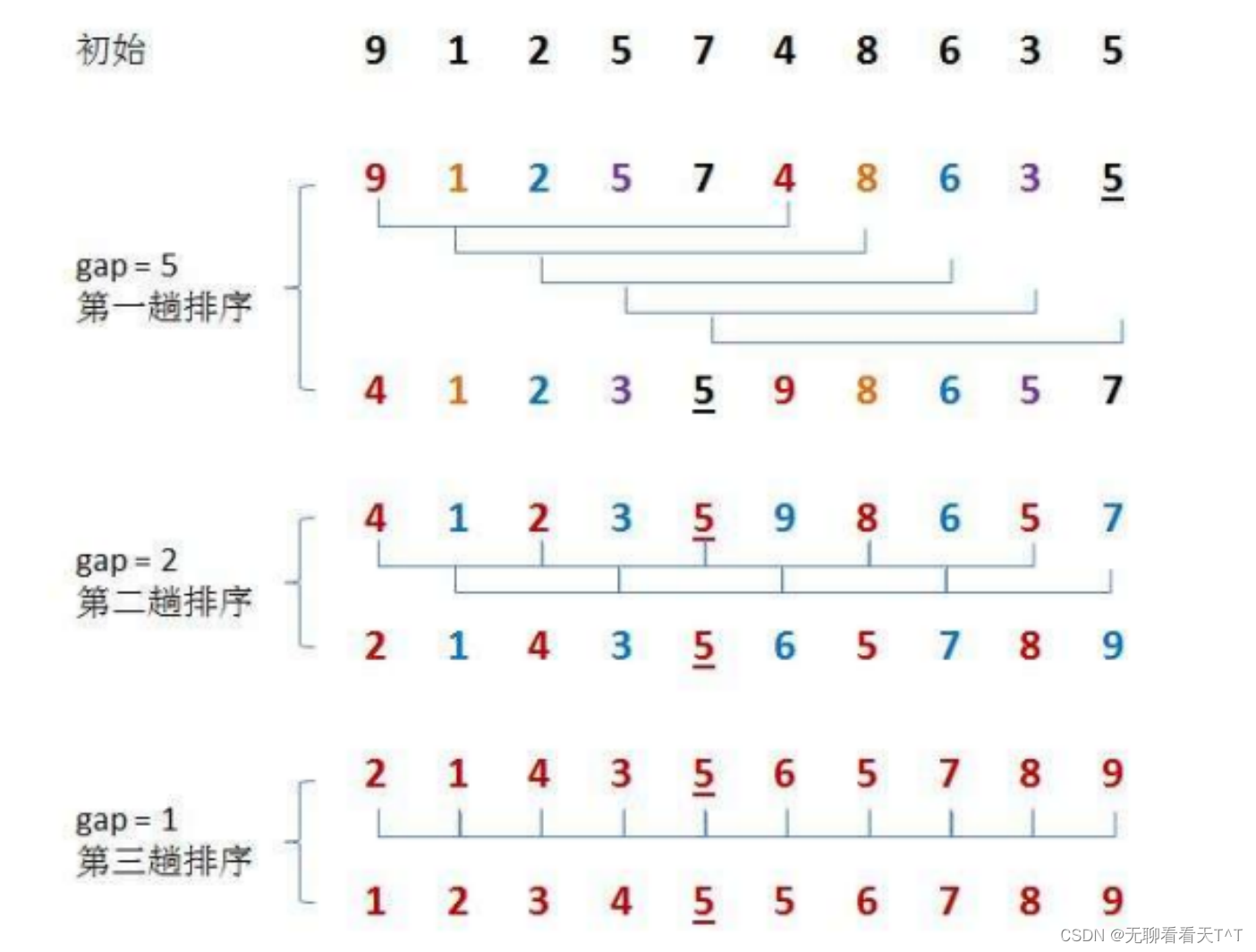
预排序
预排序有两种实现方式:顺序排序和多组并排
顺序排序
实现步骤:1、我们现在要做的不是将两个相邻的元素进行判断,而是将下标间隔为gap的元素进行直接插入排序,下图为进行一次的过程:

int gap = 3;
int end = 0;
int tmp = a[end + gap];
while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}
a[end + gap] = tmp;关于如何实现数字交换的解释:这个过程其实很有趣,首先tmp会记录每组中在后面的值,当前面的值大于后面的值时,前面的值会被赋值给后面的值得位置,此时end也会像之前那样向前走,如果初始end为0,gap为3,那么此时end=end - gap = -3 < 0,跳出循环,将存放后面值都tmp赋值给a[end + gap] = a[-3 + 3] = a[0],这样就实现了交换
2、然后我们在第一次的基础上完成一轮的排序,这时我们的end就得向前移动,我们利用外层循环的i来实现它的移动,规定在每次循环后i = i + gap,然后令循环体中的end等于此时的i即可,同时为了保证数组不会越界还需要规定i的取值不能超过n - gap,因为每次循环i都会增加gap个,有可能a[end]数组不越界,但是a[end + gap]后就数组越界了:
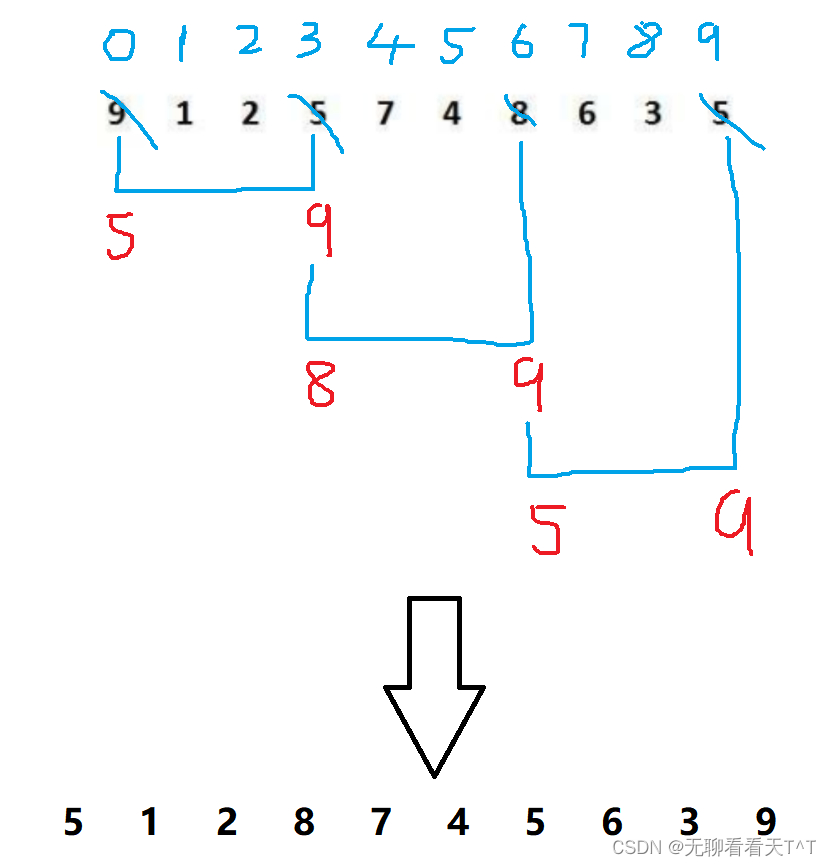
int gap = 3;
for(int i = 0;i<n-gap;i += gap)
{int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;
}3、完成一轮后,我们继续比较那些没有比较过的数,再通过一层for循环控制,此时内层for循环的i的值应该由j决定,j每次循环后只会加一(为啥要加一我真不想解释了):
int gap = 3;
for(int j = 0;j<gap;j++)
{for(int i = j;i<n-gap;i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}
}
多组并排
图有点丑,但是应该能理解吧~
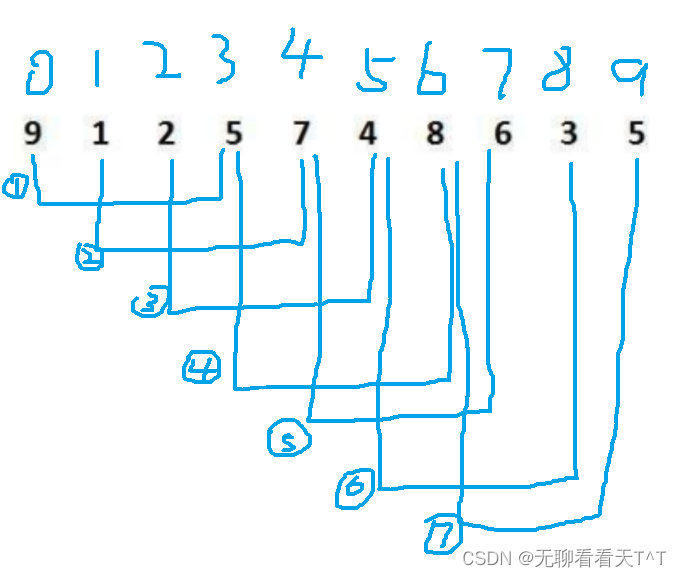
int gap = 3;
for(int i = 0;i<n-gap;++i)
{int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;
}小总结
- gap越大,大的值更快的调到后面,小的值可以更快的调到前面,越不接近有序
- gap越小,大和小的值跳的越慢,但是越接近有序,如果gap == 1预排序就是插入排序
直接插入排序
通过上面的结论我们可以发现,当gap>1时就是预排序,当gap == 1时预排序就是直接插入排序,且gap越接近于1排出来的队列就越有序,那么我们将预排序中的gap最后经过多次的预排序后让它变为1就可以实现最总的希尔排序了(gap肯定是先变为1然后进行一次直接插入排序后才会结束while循环的,所以最后不需要再多写一个直接插入排序):
int gap = n;
while(gap > 1)
{//gap = gap / 2;gap = gap / 3 + 1;for(int i = 0;i<n-gap;++i){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}
}一般情况下我们选择每次进行预排序时,将gap/2以达到gap在经历多次预排序后变为1的目的(gap的初始值无论是奇数还是偶数,最后/2必然可以得到1),但是我们更推荐令gap = gap / 3 + 1,这样可以实现更快的排序,gap将更快的被变为1(选择+1,是因为有些数比如18多次/3后会变为0,+1可以将0变为1避免了这一问题)
时空复杂度
最坏时间复杂度:O(N^2)(由于希尔排序的时间复杂度依赖于增量序列的函数,这涉及数学上尚未解决的数学难题,所以时间复杂度分析比较困难,当n在某个特定范围时,希尔排序的时间复杂度约为O(n^1.3),最坏情况下希尔排序的时间复杂度为O(N^2))
最好时间复杂度:
希尔排序的最好时间复杂度是有争议的,因为它取决于增量序列的选择和具体实现方式。在经典的希尔排序算法中,使用常见的希尔增量(gap = gap/2)作为增量序列时,最好情况下希尔排序可以达到接近O(n log n)级别的时间复杂度。这是因为较大间隔下元素会跳跃地进行比较和交换操作,使得部分元素能够快速就位。
然而,并没有一个通用且确定性质优良的最佳增量序列被找到。理论上存在一些特定情况下可以达到线性时间复杂度O(n) 的特殊增量序列选择方法。但在一般情况下,并不能保证获得更好优化后的时间复杂度。
因此,在实际应用中无法给出确切且普适可行地最佳时间复杂度定义。不同场景、不同数据集以及不同选取方式可能会导致差异结果。
需要注意,在实际应用中,对于大多数常见输入数据集来说,即便在平均和最坏情况下希尔排序也能表现出相对较高效率,并且相比于其他简单排序算法仍然具有改进之处。
空间复杂度:O(1)
希尔排序的特性
- 希尔排序是对直接插入排序的优化
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在许多书中给出的希尔排序的时间复杂度都不固定
~over~
相关文章:

直接插入排序与希尔排序
目录 前言 插入排序 直接插入排序 时空复杂度 直接插入排序的特性 希尔排序(缩小增量排序) 预排序 顺序排序 多组并排 小总结 直接插入排序 时空复杂度 希尔排序的特性 前言 字可能有点多,但是真的理解起来真的没那么难&#…...
敏捷:应对软件定义汽车时代的开发模式变革
随着软件定义汽车典型应用场景的落地,汽车从交通工具转向智能移动终端的趋势愈发明显。几十年前,一台好车的定义主要取决于高性能的底盘操稳与动力系统;几年前,一台好车的定义主要取决于智能化系统与智能交互能否满足终端用户的用…...

做题笔记:SQL Sever 方式做牛客SQL的题目--查询每天刷题通过数最多的前二名用户
----查询每天刷题通过数最多的前二名用户id和刷题数 现有牛客刷题表questions_pass_record,请查询每天刷题通过数最多的前二名用户id和刷题数,输出按照日期升序排序,查询返回结果名称和顺序为: date|user_id|pass_count 表单创建…...

Vue3 用 Proxy API 替代 defineProperty API 的那些事
一、Object.defineProperty 定义:Object.defineProperty() 方法会直接在一个对象上定义一个新属性,或者修改一个对象的现有属性,并返回此对象 1.1 为什么能实现响应式 通过defineProperty 两个属性,get及set get 属性的 gett…...
成都工业学院Web技术基础(WEB)实验五:CSS3动画制作
写在前面 1、基于2022级计算机大类实验指导书 2、代码仅提供参考,前端变化比较大,按照要求,只能做到像,不能做到一模一样 3、图片和文字仅为示例,需要自行替换 4、如果代码不满足你的要求,请寻求其他的…...
三剑客之 docker-compose文件书写项目多服务容器运行)
【Docker】学习笔记(三)三剑客之 docker-compose文件书写项目多服务容器运行
简介 引言(需求) 为了完成一个完整项目势必用到N多个容器配合完成项目中的业务开发,一旦引入N多个容器,N个容器之间就会形成某种依赖,也就意味着某个容器的运行需要其他容器优先启动之后才能正常运行; 容…...

node.js基础
node.js基础 🍓什么是node.js🍓node.js模块🍒🍒 内置模块🍅🍅🍅fs模块🍅🍅🍅path模块🍅🍅🍅http模块 🍒&#…...

fastapi实现websocket在线聊天
最近要实现一个在线聊天功能,基于fastapi的websocket实现了这个功能。下面介绍一下遇到的技术问题 1.问题难点 在线上环境部署时,一般是多进程的方式进行部署启动fastapi服务,而每个启动的进程都有自己的独立存储空间。导致存储的连接对象分…...
LLM推理部署(六):TogetherAI推出世界上LLM最快推理引擎,性能超过vLLM和TGI三倍
LLM能有多快?答案在于LLM推理的最新突破。 TogetherAI声称,他们在CUDA上构建了世界上最快的LLM推理引擎,该引擎运行在NVIDIA Tensor Core GPU上。Together推理引擎可以支持100多个开源大模型,比如Llama-2,并在Llama-2–…...
Unity | 渡鸦避难所-2 | 搭建场景并添加碰撞器
1 规范项目结构 上期中在导入一系列的商店资源包后,Assets 目录已经变的混乱不堪 开发过程中,随着资源不断更新,遵循一定的项目结构和设计规范是非常必要的。这可以增加项目的可读性、维护性、扩展性以及提高团队协作效率 这里先做下简单的…...
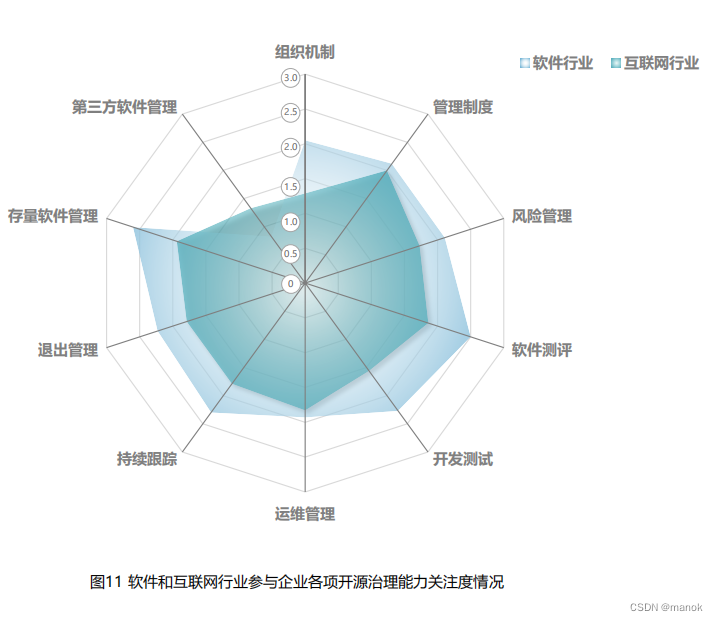
展望2024年供应链安全
2023年是开展供应链安全,尤其是开源治理如火如荼的一年,开源治理是供应链安全最重要的一个方面,所以我们从开源治理谈起。我们先回顾一下2023的开源治理情况。我们从信通院《2023年中国企业开源治理全景观察》发布的信息。信通院调研了来自七…...

React 列表页实现
一、介绍 列表页是常用的功能,从后端获取列表数据,刷新到页面上。开发列表页需要考虑以下技术要点:1.如何翻页;2.如何进行内容搜索;3.何时进行页面刷新。 二、使用教程 1.user-service 根据用户id获取用户列表,返回…...

【程序人生】还记得当初自己为什么选择计算机?
✏️ 初识计算机: 还记得人生中第一次接触计算机编程是在高中,第一门编程语言是Python(很可惜由于条件限制的原因,当时没能坚持学下去......现在想来有点后悔,没能坚持,唉......)。但是…...
、WTForms的使用)
9-tornado-Template优化方法、个人信息案例、tornado中ORM的使用(peewee的使用、peewee_async)、WTForms的使用
在很多情况下,前端模板中在很多页面有都重复的内容可以使用,比如页头、页尾、甚至中间的内容都有可能重复。这时,为了提高开发效率,我们就可以考虑在共同的部分提取出来, 主要方法有如下: 1. 模板继承 2. U…...

IDEA中.java .class .jar的含义与联系
当使用IntelliJ IDEA这样的集成开发环境进行Java编程时,通常涉及.java源代码文件、.class编译后的字节码文件以及.jar可执行的Java存档文件。 1. .java 文件: 1.这些文件包含了Java源代码,以文本形式编写。它们通常位于项目中的源代码目录中…...

北斗三号短报文森林消防应急通信及天通野外图传综合方案
森林火灾突发性强、破坏性大、危险性高,是全球发生最频繁、处置最困难、危害最严重的自然灾害之一,是生态文明建设成果和森林资源安全的最大威胁,甚至可能引发生态灾难和社会危机。我国总体上是一个缺林少绿、生态脆弱的国家,是一…...

js Array.every()的使用
2023.12.13今天我学习了如何使用Array.every()的使用,这个方法是用于检测数组中所有存在的元素。 比如我们需要判断这个数组里面的全部元素是否都包含张三,可以这样写: let demo [{id: 1, name: 张三}, {id: 2, name: 张三五}, {id: 3, name…...

前端编码中快速填充内容--乱数假文
写前端页面的时候,如果要快速插入图片,可以使用 https://picsum.photos/ 详见笔者这篇博文: 工具网站:随机生成图片的网站-CSDN博客 可是,如果要快速填充文字内容该怎么做呢? 以前,我们都是…...

数据结构二维数组计算题,以行为主?以列为主?
1.假设以行序为主序存储二维数组Aarray[1..100,1..100],设每个数据元素占2个存储单元,基地址为10,则LOC[5,5]( )。 A.808 B.818 C.1010 D&…...

springboot(ssm电影院订票信息管理系统 影院购票系统Java系统
springboot(ssm电影院订票信息管理系统 影院购票系统Java系统 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或8.0࿰…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
