Leetcode 47 全排列 II
题意理解:
首先理解全排列是什么?全排列:使用集合中所有元素按照不同元素进行排列,将所有的排列结果的集合称为全排列。
这里的全排列难度升级了,问题在于集合中的元素是可以重复的。
问题:相同的元素会导致排列重复,需要对结果进行去重操作。
难点:如何去重?
解题思路:
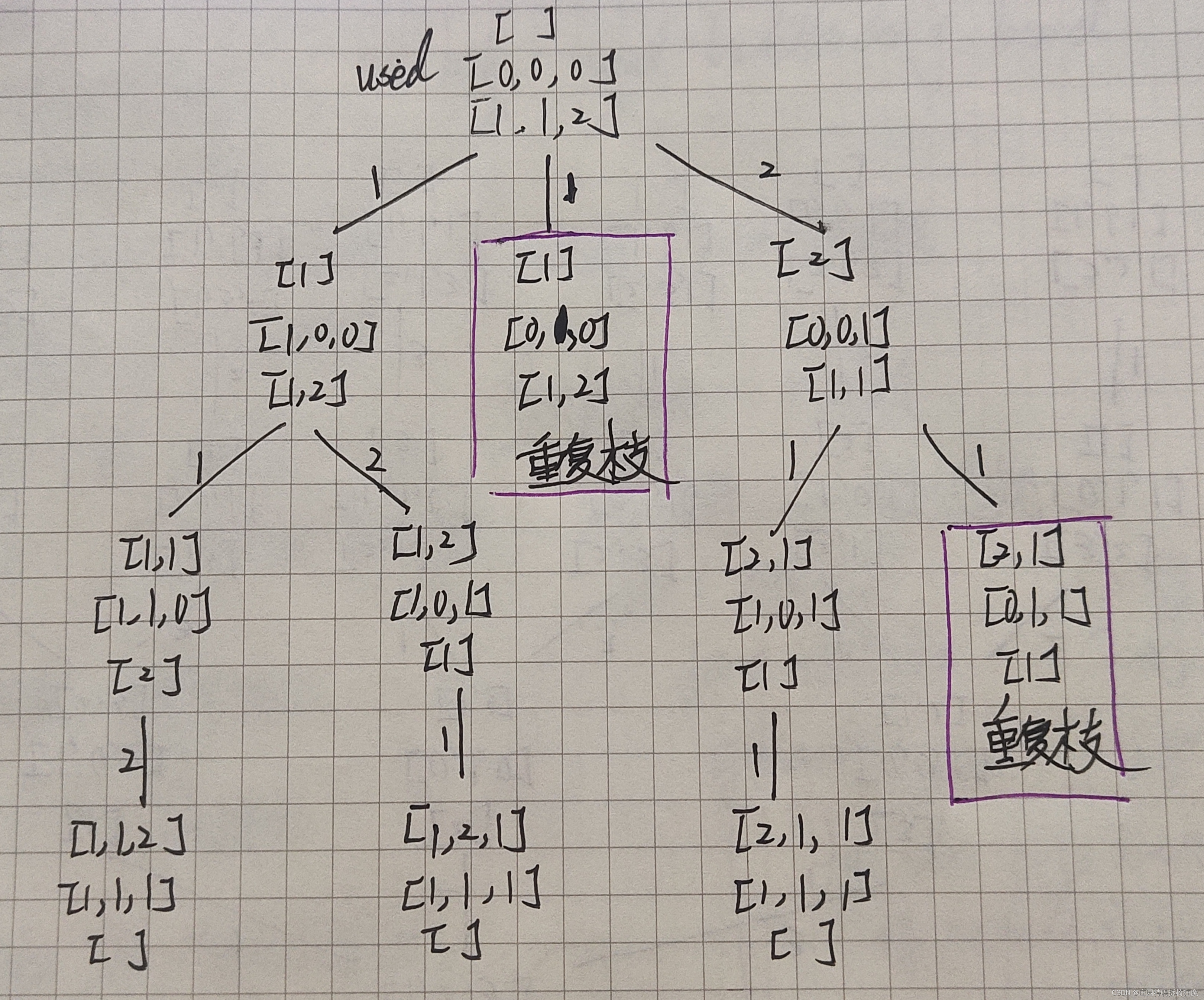
排列可以用回溯方法来进行解决。可以将其解决方案抽象为一棵树结构。
我们可以发现:
当前枝当前层,选择到重复的元素时,后出现两个相同的树枝结构,造成相同的相同的重复的结果,所以去重应该剪枝:当前枝当前层重复元素的选择。——树层去重。
为了实现树层去重:我们维护一个used[]数组来记录元素的访问状态。
used数组的作用:
保证所有元素只是用一次。
来辅助树层去重操作。
1.暴力回溯+剪枝优化
回溯解决问题的三个关键步骤:
确定返回值和参数列表
确定终止条件
确定单层递归逻辑:1.保证元素只用一次 2.树层剪枝,防止重复值造成结果重复。
List<List<Integer>> result=new ArrayList<>();LinkedList<Integer> path=new LinkedList<>();boolean[] used=null;public List<List<Integer>> permuteUnique(int[] nums) {Arrays.sort(nums);used=new boolean[nums.length];//初始化默认值falsebacktracking(nums);return result;}public void backtracking(int[] nums){//确定终止条件if(path.size()== nums.length){result.add(new ArrayList<>(path));return;}//单层递归逻辑for(int i=0;i<nums.length;i++){if(used[i]==true) continue;//该元素用过if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false) continue;//同枝同层剪枝path.add(nums[i]);used[i]=true;backtracking(nums);path.removeLast();used[i]=false;}}2.分析
时间复杂度:O(n×n!)
空间复杂度:O(n)
相关文章:
Leetcode 47 全排列 II
题意理解: 首先理解全排列是什么?全排列:使用集合中所有元素按照不同元素进行排列,将所有的排列结果的集合称为全排列。 这里的全排列难度升级了,问题在于集合中的元素是可以重复的。 问题:相同的元素会导致…...
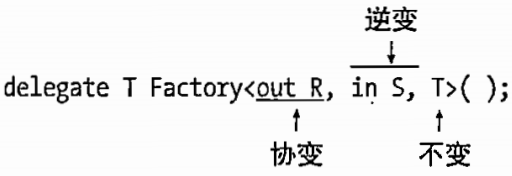
C# 图解教程 第5版 —— 第18章 泛型
文章目录 18.1 什么是泛型18.2 C# 中的泛型18.3 泛型类18.3.1 声明泛型类18.3.2 创建构造类型18.3.3 创建变量和实例18.3.4 使用泛型的示例18.3.5 比较泛型和非泛型栈 18.4 类型参数的约束18.4.1 Where 子句18.4.2 约束类型和次序 18.5 泛型方法18.5.1 声明泛型方法18.5.2 调用…...

保障事务隔离级别的关键措施
目录 引言 1. 锁机制的应用 2. 多版本并发控制(MVCC)的实现 3. 事务日志的记录与恢复 4. 数据库引擎的实现策略 结论 引言 事务隔离级别是数据库管理系统(DBMS)中的一个关键概念,用于控制并发事务之间的可见性。…...

Docker导入导出镜像、导入导出容器的命令详解以及使用的场景
一、Docker 提供用于管理镜像和容器命令 1.1 docker save 与 docker load 这是一对操作,用于处理 Docker 镜像。这个操作会将所有的镜像层以及元数据打包到一个 tar 文件中。然后,你可以使用 docker load 命令将这个 tar 文件导入到任何 Docker 环境中…...
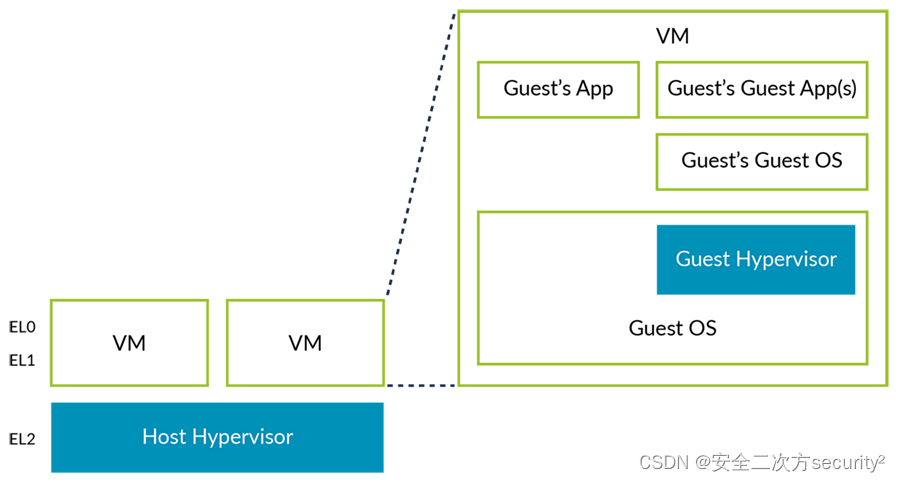
虚拟化嵌套
在理论上,可以在虚拟机(VM)内运行一个hypervisor,这个概念被称为嵌套虚拟化: 我们将第一个hypervisor称为Host Hypervisor,将VM内的hypervisor称为Guest Hypervisor。 在Armv8.3-A发布之前,可以通过在EL0中运行Guest Hypervisor来在VM中运行Guest Hypervisor。然而,这…...

【XILINX】记录ISE/Vivado使用过程中遇到的一些warning及解决方案
前言 XILINX/AMD是大家常用的FPGA,但是在使用其开发工具ISE/Vivado时免不了会遇到很多warning,(大家是不是发现程序越大warning越多?),并且还有很多warning根据消除不了,看着特心烦? 我这里汇总一些我遇到的…...
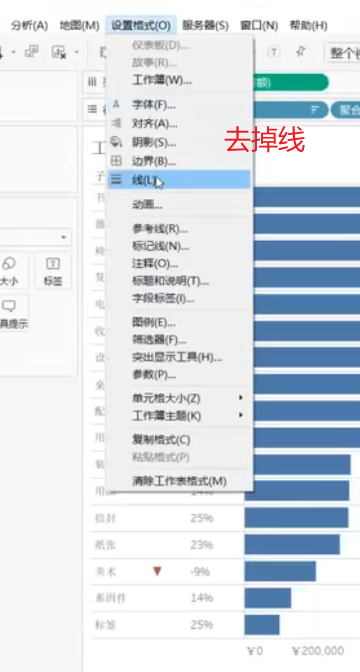
Tableau进阶--Tableau数据故事慧(20)解构Tableau的绘图逻辑
官网介绍 官网连接如下: https://www.tableau.com/zh-cn tableau的产品包括如下: 参考:https://zhuanlan.zhihu.com/p/341882097 Tableau是功能强大、灵活且安全些很高的端到端的数据分析平台,它提供了从数据准备、连接、分析、协作到查阅…...
)
45.0/HTML 简介(详细版)
目录 45.1 互联网简介 45.2 网页技术与分类 45.3 HTML 简介 45.3.1 什么是 HTML?(面试题) 45.3.2 HTML 文件结构 45.3.3 HTML 语法 45.3.4 实例演练步骤(面试题) 45.4 head 中的常用标签 45.4.1 title 标记 45.4.2 meta 标记 45.4.3 45.4.4 45.4.4(面试题)总结: 45…...

Python 如何进行游戏开发?
游戏开发是一个广泛的领域,Python 作为一门灵活的编程语言,可以用于不同类型的游戏开发。以下是一些建议和步骤,帮助你开始使用 Python 进行游戏开发: 1、选择游戏开发库/框架: Pygame: Pygame 是一个用于…...

到底什么是DevOps
DevOps不是一组工具,也不是一个特定的岗位。在我看来DevOps更像是一种软件开发文化,一种实现快速交付能力的手段。 DevOps 强调的是高效组织团队之间如何通过自动化的工具协作和沟通来完成软件的生命周期管理,从而更快、更频繁地交付更稳定的…...

Keil生成bin文件
Keil生成bin文件_keil5生成bin文件-CSDN博客...
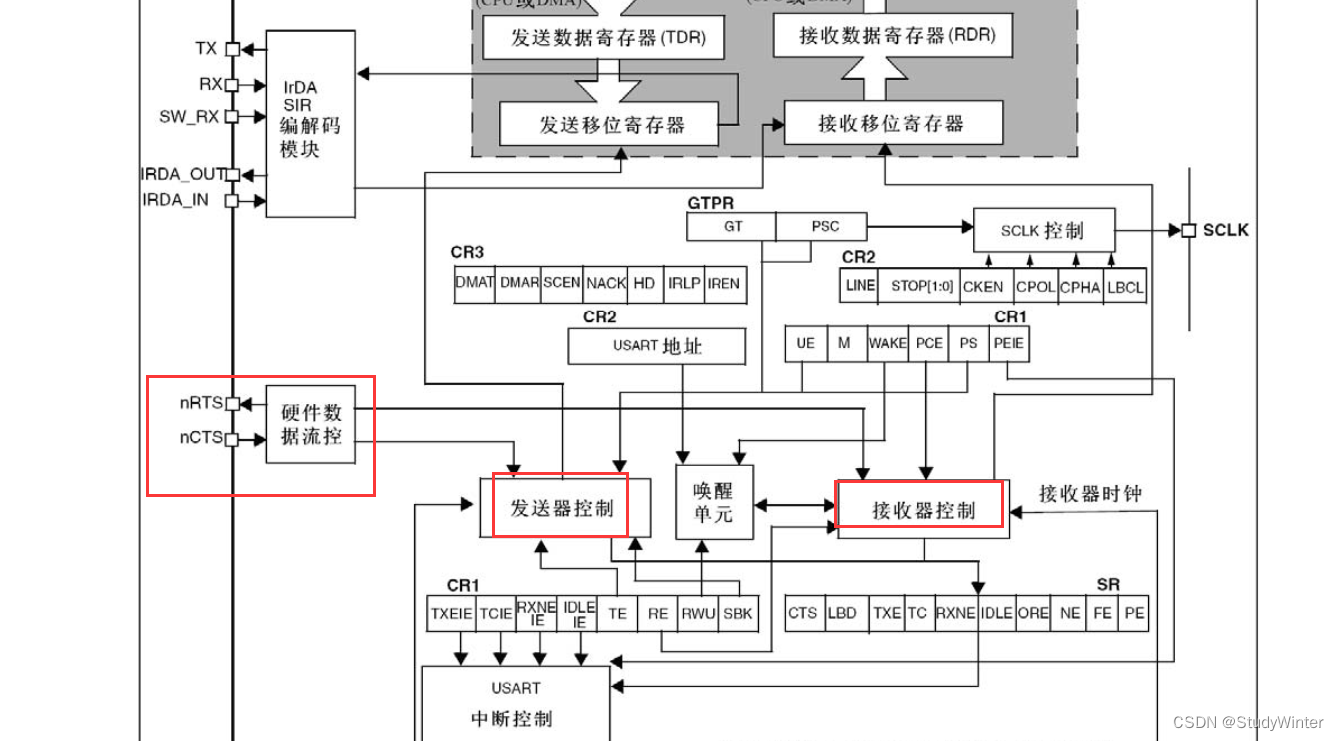
【STM32】USART串口协议
1 通信接口 通信的目的:将一个设备的数据传送到另一个设备,扩展硬件系统 通信协议:制定通信的规则,通信双方按照协议规则进行数据收发 USRT:TX是数据发送引脚,RX是数据接受引脚; I2C…...

淋雨试验箱
产品概述 KDZD-IPX34淋雨试验箱是对户外电子电工产品的防水性能测试的一种装置。该设备通过不同尺寸的喷嘴喷水,产品外壳表面淋水冲洗来检测防水性能。在测试物品时,将样品放在转台上,试验启动时,水流通过压力计和流量计控制水…...
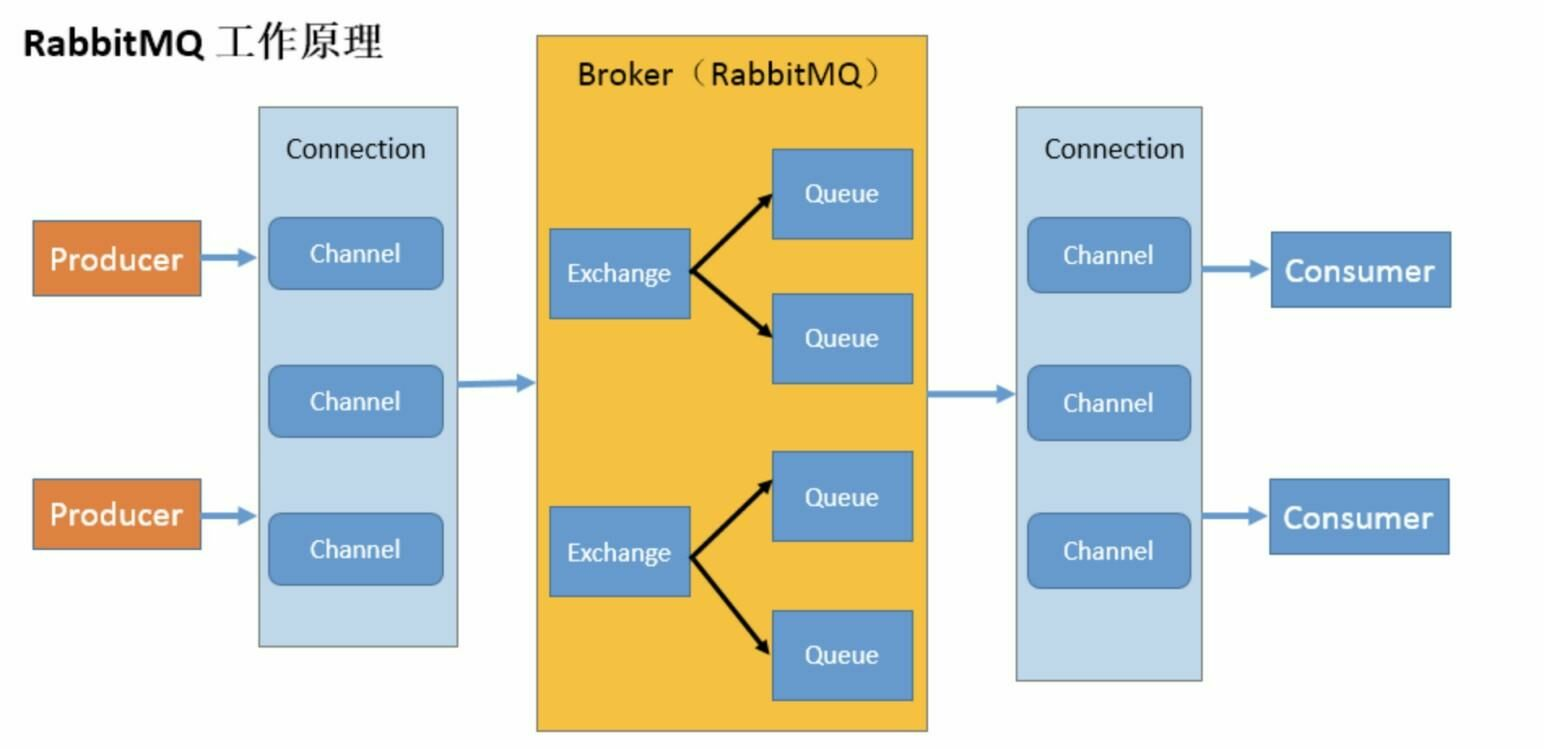
02-MQ入门之RabbitMQ简单概念说明
二:RabbitMQ 介绍 1.RabbitMQ的概念 RabbitMQ 是一个消息中间件:它接受并转发消息。你可以把它当做一个快递站点,当你要发送一个包裹时,你把你的包裹放到快递站,快递员最终会把你的快递送到收件人那里,按…...
敏感信息泄漏怎么破?来试试极狐GitLab 的密钥检测吧
前言 在应用程序开发过程中,一个很常见的问题就是:开发人员为了本地 debug 方便,会 hardcode 一些信息,比如连接数据库的用户名、密码、连接第三方 app 的 token、certificate 等,如果在提交代码的时候没有及时删除 ha…...

go学习之网络编程
文章目录 网络编程1、网络编程的基本介绍2.网络编程的基础知识1)协议(tcp/ip)2)OSI与TCP/ip参考模型3)ip地址4)端口(port)介绍5)tcp socket编程的客户端和服务器端 3.socket编程快速入门4.经典项目-海量用户即时通讯系…...

将数组中的数逆序存放
本题要求编写程序,将给定的n个整数存入数组中,将数组中的这n个数逆序存放,再按顺序输出数组中的元素。 输入格式: 输入在第一行中给出一个正整数n(1≤n≤10)。第二行输入n个整数,用空格分开。 输出格式:…...

Unity Web 浏览器-3D WebView中有关于CanvasWebViewPrefab
一、CanvasWebViewPrefab默认设置 这个是在2_CanvasWebViewDemo示例场景文件中可以可以查看得到,可以看出CanvasWebViewPrefab的默认配置如下。 二、Web 浏览器网页和Unity内置UI的渲染顺序 1、如果你勾选了以下这个Native 2D Mode选项的话,那么Unit…...
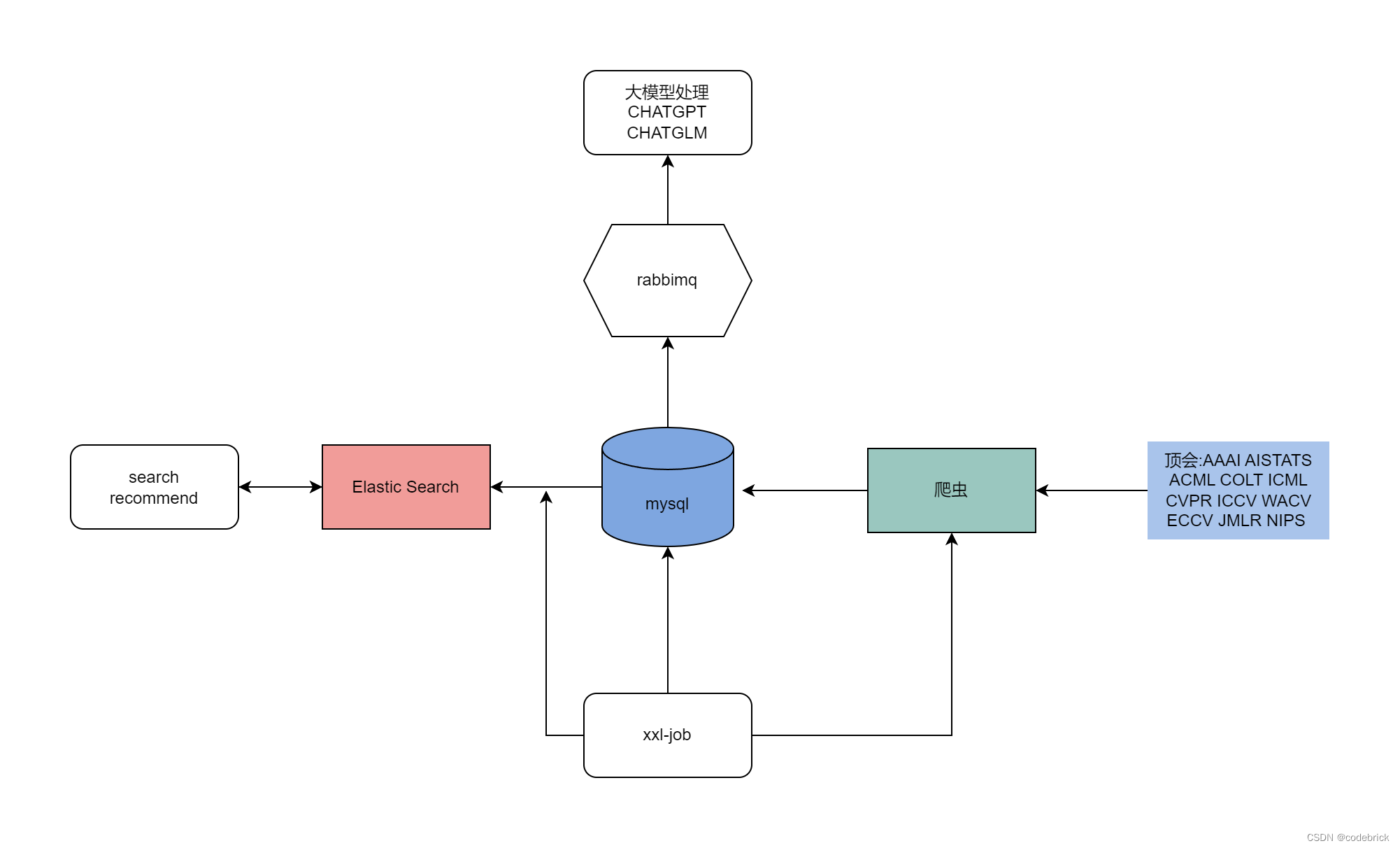
一款计算机顶会爬取解析系统 paper info
一款计算机顶会爬取解析系统 paper info 背景项目实现的功能 技术方案架构设计项目使用的技术选型 使用方法本地项目部署使用ChatGPT等大模型创建一个ChatGPT助手使用阿里云 顶会数据量 百度网盘pfd文件json文件 Q&A github链接 :https://github.com/codebricki…...

CommonJs模块化实现原理ES Module模块化原理
CommonJs模块化实现原理 首先看一个案例 初始化项目 npm init npm i webpack -D目录结构如下: webpack.config.js const path require("path"); module.exports {mode: "development",entry: "./src/index.js",output: {path: p…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

LeetCode 0386.字典序排数:细心总结条件
【LetMeFly】386.字典序排数:细心总结条件 力扣题目链接:https://leetcode.cn/problems/lexicographical-numbers/ 给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。 你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。…...

STM32 低功耗设计全攻略:PWR 模块原理 + 睡眠 / 停止 / 待机模式实战(串口 + 红外 + RTC 应用全解析)
文章目录 PWRPWR(电源控制模块)核心功能 电源框图上电复位和掉电复位可编程电压监测器低功耗模式模式选择睡眠模式停止模式待机模式 修改主频一、准备工作二、修改主频的核心步骤:宏定义配置三、程序流程:时钟配置函数解析四、注意…...
