逆向获取某音乐软件的加密(js逆向)
本文仅用于技术交流,不得以危害或者是侵犯他人利益为目的使用文中介绍的代码模块,若有侵权请联系作者更改。
老套路,打开开发者工具,直接开始找到需要的数据位置,然后观察参数,请求头,cookie是否加密,我相信这部分内容大家都比较清楚。
第一个基本上,你均不影响结果,重要的还是他下方的内容
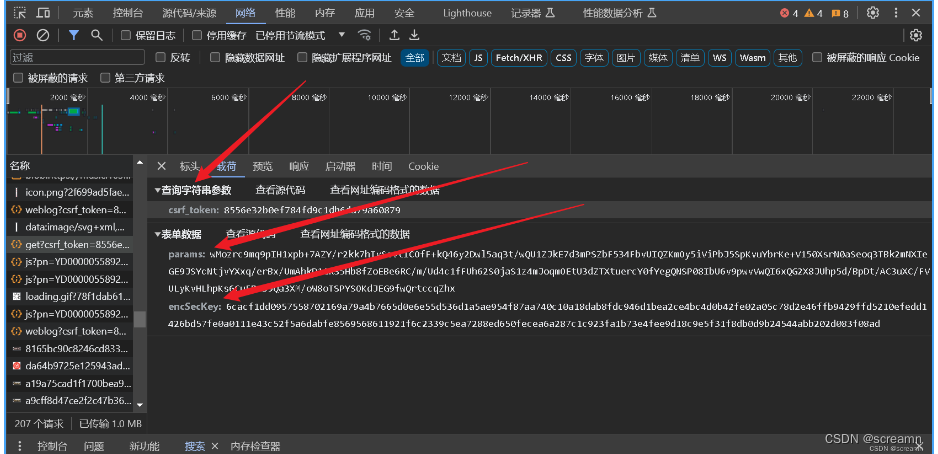
现在我们直接来照这个params参数,直接搜索,也可以打XHR断点快速找到这个位置,但是这里的话我推荐大家直接搜索,因为这个加密的参数不是字母代替的,而是一个英文单词,这样搜出来的内容可能会比xhr断点得到的更为准确,要是说加密参数是m="密文这种",如果搜m=或者=m均出现大量情况的话,分析请求再来决定使用什么方法快速定位。
这边直接搜索,搜出来的也不少,但是他们均在一个文件中,那么我们可以缩小查找范围了,先开始点击查看。

进入文件后,直接搜索encSecKey,观察这里面是不是存在这个参数,直接找到,加密的两个参数的位置,所以说很多时候这种查找都是有技巧的,实在不行才去一个一个的查看。
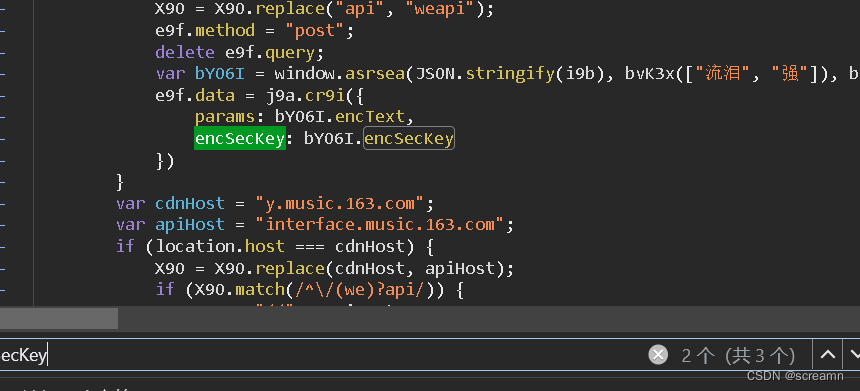
剩下的就是扣代码了,这个我只带大家扣一部分的代码,完整的还得大家去扣,主要是里面有些一些小坑,带大家过一下就行,剩下的纯缺啥补啥。
打上断点,开始调试
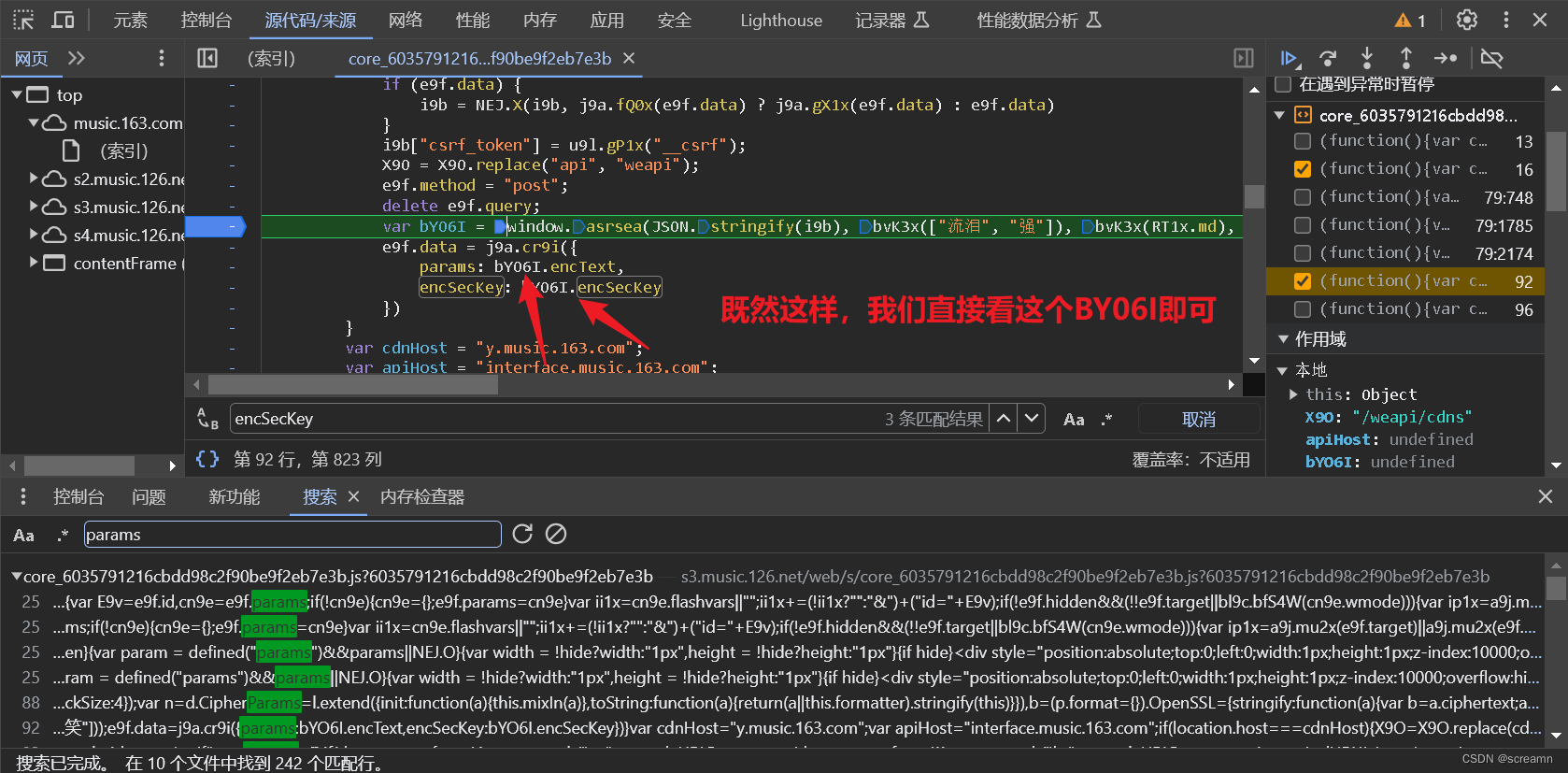
依次解析这里面的参数,避免存在加密的。固定值,多刷新几次发现没有改变。

依次进行后面的参数验证,我们发现全部都是常量,所以直接记录下来,直接拿来用。
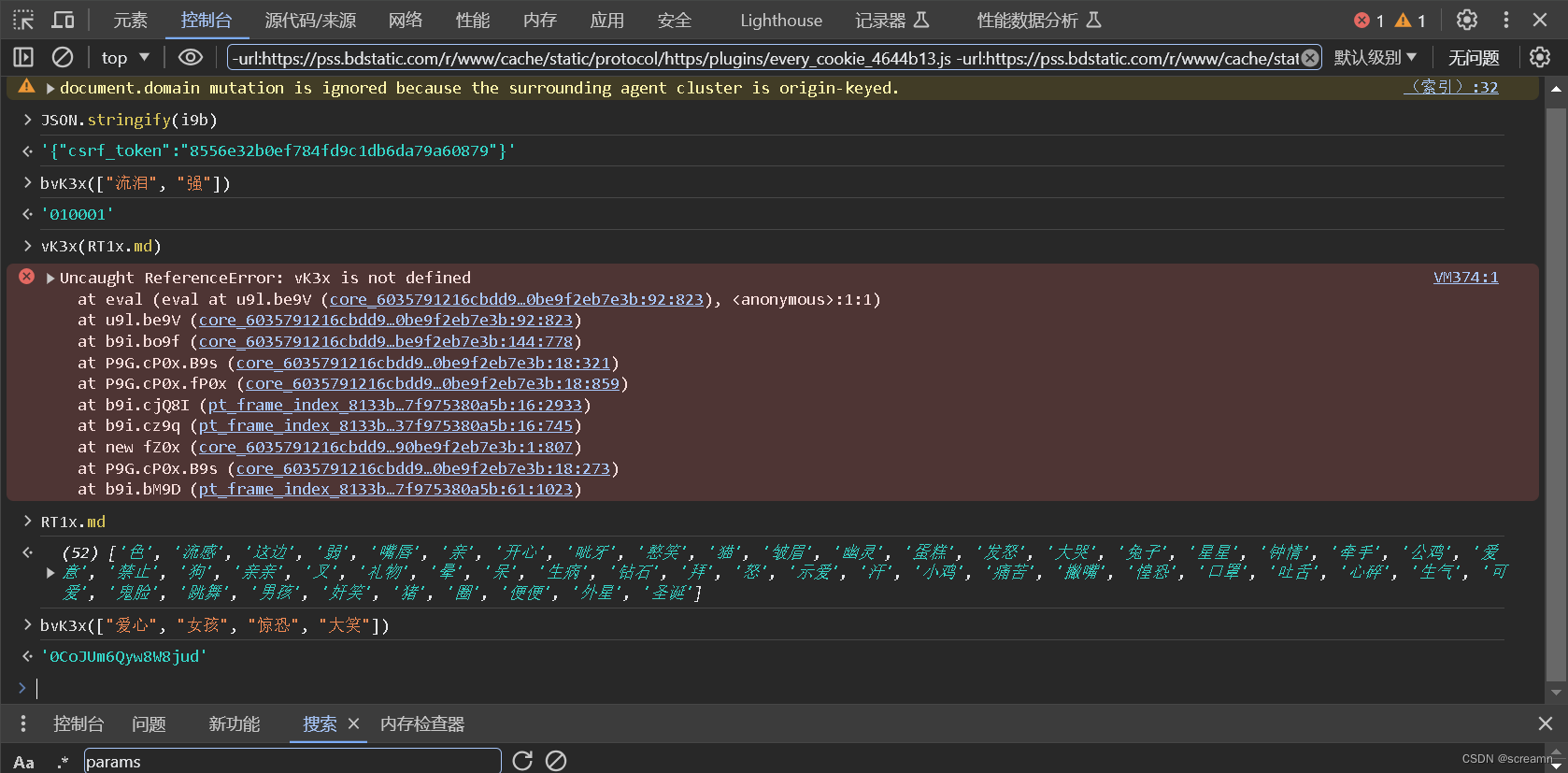
现在开始找加密形式。


开始补全这个内容,发现少a继续扣。
有其他的参数,扣下来a,继续扣。
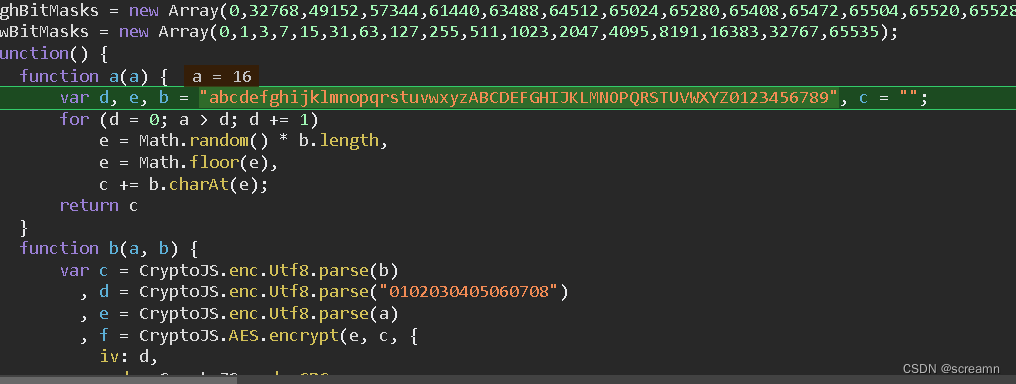
这个b函数我们需要注意一下,这里面 的加密是通过js中的库函数加密的,所以我们在js中直接引用即可,剩下的都是扣代码,这边给出后续扣下来的代码。
function arrayCopy(a, b, c, d, e) {var g, h, f = Math.min(b + e, a.length);for (g = b,h = d; f > g; ++g,++h)c[h] = a[g]
}
function biFromNumber(a) {var c, b = new BigInt;for (b.isNeg = 0 > a,a = Math.abs(a),c = 0; a > 0;)b.digits[c++] = a & maxDigitVal,a >>= biRadixBits;return b
}
function reverseStr(a) {var c, b = "";for (c = a.length - 1; c > -1; --c)b += a.charAt(c);return b
}
function digitToHex(a) {var b = 15, c = "";for (i = 0; 4 > i; ++i)c += hexToChar[a & b],a >>>= 4;return reverseStr(c)
}
function biToHex(a) {var d, b = "";for (biHighIndex(a),d = biHighIndex(a); d > -1; --d)b += digitToHex(a.digits[d]);return b
}
function biModuloByRadixPower(a, b) {var c = new BigInt;return arrayCopy(a.digits, 0, c.digits, 0, b),c
}
function biDivideByRadixPower(a, b) {var c = new BigInt;return arrayCopy(a.digits, b, c.digits, 0, c.digits.length - b),c
}
function biMultiply(a, b) {var d, h, i, k, c = new BigInt, e = biHighIndex(a), f = biHighIndex(b);for (k = 0; f >= k; ++k) {for (d = 0,i = k,j = 0; e >= j; ++j,++i)h = c.digits[i] + a.digits[j] * b.digits[k] + d,c.digits[i] = h & maxDigitVal,d = h >>> biRadixBits;c.digits[k + e + 1] = d}return c.isNeg = a.isNeg != b.isNeg,c
}
function BarrettMu_multiplyMod(a, b) {var c = biMultiply(a, b);return this.modulo(c)
}
function BarrettMu_powMod(a, b) {var d, e, c = new BigInt;for (c.digits[0] = 1,d = a,e = b; ;) {if (0 != (1 & e.digits[0]) && (c = this.multiplyMod(c, d)),e = biShiftRight(e, 1),0 == e.digits[0] && 0 == biHighIndex(e))break;d = this.multiplyMod(d, d)}return c
}
function BarrettMu_modulo(a) {var i, b = biDivideByRadixPower(a, this.k - 1), c = biMultiply(b, this.mu), d = biDivideByRadixPower(c, this.k + 1), e = biModuloByRadixPower(a, this.k + 1), f = biMultiply(d, this.modulus), g = biModuloByRadixPower(f, this.k + 1), h = biSubtract(e, g);for (h.isNeg && (h = biAdd(h, this.bkplus1)),i = biCompare(h, this.modulus) >= 0; i;)h = biSubtract(h, this.modulus),i = biCompare(h, this.modulus) >= 0;return h
}
function biMultiplyByRadixPower(a, b) {var c = new BigInt;return arrayCopy(a.digits, 0, c.digits, b, c.digits.length - b),c
}
function biShiftRight(a, b) {var e, f, g, h, c = Math.floor(b / bitsPerDigit), d = new BigInt;for (arrayCopy(a.digits, c, d.digits, 0, a.digits.length - c),e = b % bitsPerDigit,f = bitsPerDigit - e,g = 0,h = g + 1; g < d.digits.length - 1; ++g,++h)d.digits[g] = d.digits[g] >>> e | (d.digits[h] & lowBitMasks[e]) << f;return d.digits[d.digits.length - 1] >>>= e,d.isNeg = a.isNeg,d
}
function biMultiplyDigit(a, b) {var c, d, e, f;for (result = new BigInt,c = biHighIndex(a),d = 0,f = 0; c >= f; ++f)e = result.digits[f] + a.digits[f] * b + d,result.digits[f] = e & maxDigitVal,d = e >>> biRadixBits;return result.digits[1 + c] = d,result
}
function biSubtract(a, b) {var c, d, e, f;if (a.isNeg != b.isNeg)b.isNeg = !b.isNeg,c = biAdd(a, b),b.isNeg = !b.isNeg;else {for (c = new BigInt,e = 0,f = 0; f < a.digits.length; ++f)d = a.digits[f] - b.digits[f] + e,c.digits[f] = 65535 & d,c.digits[f] < 0 && (c.digits[f] += biRadix),e = 0 - Number(0 > d);if (-1 == e) {for (e = 0,f = 0; f < a.digits.length; ++f)d = 0 - c.digits[f] + e,c.digits[f] = 65535 & d,c.digits[f] < 0 && (c.digits[f] += biRadix),e = 0 - Number(0 > d);c.isNeg = !a.isNeg} elsec.isNeg = a.isNeg}return c
}
function biCompare(a, b) {if (a.isNeg != b.isNeg)return 1 - 2 * Number(a.isNeg);for (var c = a.digits.length - 1; c >= 0; --c)if (a.digits[c] != b.digits[c])return a.isNeg ? 1 - 2 * Number(a.digits[c] > b.digits[c]) : 1 - 2 * Number(a.digits[c] < b.digits[c]);return 0
}
function biShiftLeft(a, b) {var e, f, g, h, c = Math.floor(b / bitsPerDigit), d = new BigInt;for (arrayCopy(a.digits, 0, d.digits, c, d.digits.length - c),e = b % bitsPerDigit,f = bitsPerDigit - e,g = d.digits.length - 1,h = g - 1; g > 0; --g,--h)d.digits[g] = d.digits[g] << e & maxDigitVal | (d.digits[h] & highBitMasks[e]) >>> f;return d.digits[0] = d.digits[g] << e & maxDigitVal,d.isNeg = a.isNeg,d
}
var maxDigits, ZERO_ARRAY, bigZero, bigOne, dpl10, lr10, hexatrigesimalToChar, hexToChar, highBitMasks, lowBitMasks, biRadixBase = 2, biRadixBits = 16, bitsPerDigit = biRadixBits, biRadix = 65536, biHalfRadix = biRadix >>> 1, biRadixSquared = biRadix * biRadix, maxDigitVal = biRadix - 1, maxInteger = 9999999999999998;
setMaxDigits(20),dpl10 = 15,lr10 = biFromNumber(1e15),hexatrigesimalToChar = new Array("0", "1", "2", "3", "4", "5", "6", "7", "8", "9", "a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p", "q", "r", "s", "t", "u", "v", "w", "x", "y", "z"),hexToChar = new Array("0", "1", "2", "3", "4", "5", "6", "7", "8", "9", "a", "b", "c", "d", "e", "f"),highBitMasks = new Array(0, 32768, 49152, 57344, 61440, 63488, 64512, 65024, 65280, 65408, 65472, 65504, 65520, 65528, 65532, 65534, 65535),lowBitMasks = new Array(0, 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047, 4095, 8191, 16383, 32767, 65535);function biNumBits(a) {var e, b = biHighIndex(a), c = a.digits[b], d = (b + 1) * bitsPerDigit;for (e = d; e > d - bitsPerDigit && 0 == (32768 & c); --e)c <<= 1;return e
}
function biDivideModulo(a, b) {var f, g, h, i, j, k, l, m, n, o, p, q, r, s, c = biNumBits(a), d = biNumBits(b), e = b.isNeg;if (d > c)return a.isNeg ? (f = biCopy(bigOne),f.isNeg = !b.isNeg,a.isNeg = !1,b.isNeg = !1,g = biSubtract(b, a),a.isNeg = !0,b.isNeg = e) : (f = new BigInt,g = biCopy(a)),new Array(f, g);for (f = new BigInt,g = a,h = Math.ceil(d / bitsPerDigit) - 1,i = 0; b.digits[h] < biHalfRadix;)b = biShiftLeft(b, 1),++i,++d,h = Math.ceil(d / bitsPerDigit) - 1;for (g = biShiftLeft(g, i),c += i,j = Math.ceil(c / bitsPerDigit) - 1,k = biMultiplyByRadixPower(b, j - h); -1 != biCompare(g, k);)++f.digits[j - h],g = biSubtract(g, k);for (l = j; l > h; --l) {for (m = l >= g.digits.length ? 0 : g.digits[l],n = l - 1 >= g.digits.length ? 0 : g.digits[l - 1],o = l - 2 >= g.digits.length ? 0 : g.digits[l - 2],p = h >= b.digits.length ? 0 : b.digits[h],q = h - 1 >= b.digits.length ? 0 : b.digits[h - 1],f.digits[l - h - 1] = m == p ? maxDigitVal : Math.floor((m * biRadix + n) / p),r = f.digits[l - h - 1] * (p * biRadix + q),s = m * biRadixSquared + (n * biRadix + o); r > s;)--f.digits[l - h - 1],r = f.digits[l - h - 1] * (p * biRadix | q),s = m * biRadix * biRadix + (n * biRadix + o);k = biMultiplyByRadixPower(b, l - h - 1),g = biSubtract(g, biMultiplyDigit(k, f.digits[l - h - 1])),g.isNeg && (g = biAdd(g, k),--f.digits[l - h - 1])}return g = biShiftRight(g, i),f.isNeg = a.isNeg != e,a.isNeg && (f = e ? biAdd(f, bigOne) : biSubtract(f, bigOne),b = biShiftRight(b, i),g = biSubtract(b, g)),0 == g.digits[0] && 0 == biHighIndex(g) && (g.isNeg = !1),new Array(f, g)
}
function biDivide(a, b) {return biDivideModulo(a, b)[0]
}
function biCopy(a) {var b = new BigInt(!0);return b.digits = a.digits.slice(0),b.isNeg = a.isNeg,b
}
function BarrettMu(a) {this.modulus = biCopy(a),this.k = biHighIndex(this.modulus) + 1;var b = new BigInt;b.digits[2 * this.k] = 1,this.mu = biDivide(b, this.modulus),this.bkplus1 = new BigInt,this.bkplus1.digits[this.k + 1] = 1,this.modulo = BarrettMu_modulo,this.multiplyMod = BarrettMu_multiplyMod,this.powMod = BarrettMu_powMod
}
function charToHex(a) {var h, b = 48, c = b + 9, d = 97, e = d + 25, f = 65, g = 90;return h = a >= b && c >= a ? a - b : a >= f && g >= a ? 10 + a - f : a >= d && e >= a ? 10 + a - d : 0
}
function hexToDigit(a) {var d, b = 0, c = Math.min(a.length, 4);for (d = 0; c > d; ++d)b <<= 4,b |= charToHex(a.charCodeAt(d));return b
}
function biFromHex(a) {var d, e, b = new BigInt, c = a.length;for (d = c,e = 0; d > 0; d -= 4,++e)b.digits[e] = hexToDigit(a.substr(Math.max(d - 4, 0), Math.min(d, 4)));return b
}
function BigInt(a) {this.digits = "boolean" == typeof a && 1 == a ? null : ZERO_ARRAY.slice(0),this.isNeg = !1
}
function biHighIndex(a) {for (var b = a.digits.length - 1; b > 0 && 0 == a.digits[b];)--b;return b
}
var CryptoJS = require('crypto-js')
function b(a, b) {var f = ""var c = CryptoJS.enc.Utf8.parse(b), d = CryptoJS.enc.Utf8.parse("0102030405060708"), e = CryptoJS.enc.Utf8.parse(a), f = CryptoJS.AES.encrypt(e, c, {iv: d,mode: CryptoJS.mode.CBC});return f.toString()
}
function a(a) {var d, e, b = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789", c = "";for (d = 0; a > d; d += 1)e = Math.random() * b.length,e = Math.floor(e),c += b.charAt(e);return c
}
function setMaxDigits(a) {maxDigits = a,ZERO_ARRAY = new Array(maxDigits);for (var b = 0; b < ZERO_ARRAY.length; b++)ZERO_ARRAY[b] = 0;bigZero = new BigInt,bigOne = new BigInt,bigOne.digits[0] = 1
}
function encryptedString(a, b) {for (var f, g, h, i, j, k, l, c = new Array, d = b.length, e = 0; d > e;)c[e] = b.charCodeAt(e),e++;for (; 0 != c.length % a.chunkSize;)c[e++] = 0;for (f = c.length,g = "",e = 0; f > e; e += a.chunkSize) {for (j = new BigInt,h = 0,i = e; i < e + a.chunkSize; ++h)j.digits[h] = c[i++],j.digits[h] += c[i++] << 8;k = a.barrett.powMod(j, a.e),l = 16 == a.radix ? biToHex(k) : biToString(k, a.radix),g += l + " "}return g.substring(0, g.length - 1)
}
function RSAKeyPair(a, b, c) {this.e = biFromHex(a),this.d = biFromHex(b),this.m = biFromHex(c),this.chunkSize = 2 * biHighIndex(this.m),this.radix = 16,this.barrett = new BarrettMu(this.m)
}
function c(a, b, c) {var d, e;return setMaxDigits(131),d = new RSAKeyPair(b, "", c),e = encryptedString(d, a)
}function cr8j(gF9w) {return (gF9w, "&", !0)
}基本的思路学习,然后自己着手写一次,理解会更多,点个赞再走吧!
相关文章:

逆向获取某音乐软件的加密(js逆向)
本文仅用于技术交流,不得以危害或者是侵犯他人利益为目的使用文中介绍的代码模块,若有侵权请联系作者更改。 老套路,打开开发者工具,直接开始找到需要的数据位置,然后观察参数,请求头,cookie是…...
C语言—每日选择题—Day42
第一题 1. 下面程序输出的结果是() #include <stdio.h> int main () {int x;x printf("I See, Sea in C");printf("x%d" , x); } A:2 B:随机值 C:都不是 D:15 答案及解析 D p…...

jsp文件引用的css修改后刷新不生效问题
问题 在对 JavaWeb 项目修改的过程中,发现修改了 jsp 文件引入的 css 文件的代码后页面的样式没有更新的问题。 原因 导致这个问题的原因可能是因为浏览器缓存的问题。 解决方法 下面介绍两种解决方法,供大家参考: 1、给 link 标签的 c…...
SpringBoot运维中的高级配置
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开心好久好久😎 📚系列专栏:Java全栈,…...

Centos7下OpenLDAP安装
openldap server 安装配置 openldap server 安装 # yum 安装相关包 $ sudo yum -y install openldap openldap-servers openldap-devel compat-openldap openldap-clients# 复制一个默认配置到指定目录下,并授权,这一步一定要做,然后再启动服务,不然生产密码时会报错 # Op…...

2036开关门,1109开关门
一:2036开关门 1.1题目 1.2思路 1.每次都是房间号是服务员的倍数的时候做处理,所以外层(i)枚举服务员1~n,内层(j)枚举房间号1~n,当j % i0时,做处理 2.这个处理指的是&…...
最简单的pixel刷机和安装面具、lsposed
一 下载手机对应的系统 1,手机usb连接然后重启进入Fastboot模式:adb reboot bootloader2,找到你下载的系统,Windows 系统 直接运行 flash-all.bat上图 :左边就是安卓11和12的系统,右边是对应的手机型号 下…...

深度学习第5天:GAN生成对抗网络
☁️主页 Nowl 🔥专栏 《深度学习》 📑君子坐而论道,少年起而行之 文章目录 一、GAN1.基本思想2.用途3.模型架构 二、具体任务与代码1.任务介绍2.导入库函数3.生成器与判别器4.预处理5.模型训练6.图片生成7.不同训练轮次的结果对比 一…...

从零开始搭建企业管理系统(七):RBAC 之用户管理
RBAC 之用户管理 创建表(Entity)用户表角色表权限表用户角色表关系注解ManyToMany 角色权限表 接口开发UserControllerUserServiceUserServiceImplUserRepository 问题解决update 更新问题懒加载问题JSON 循环依赖问题 根据上一小结对表的设计࿰…...
phpstudy搭建WordPress教程
一、phpstudy新建配置WordPress 打开phpstudy,启动Apache(或者Nginx)和MySQL服务 来到数据库部分,点击[创建数据库],填写新建数据库的名称,用户名以及密码,完成后点击确认 来到网站部分&#x…...

typedef的使用
在C语言中,有一个关键字叫做typedef,有些人对此感到很疑惑。不熟悉此知识的同学都会对编程失去细心,直接劝退(因为之前我就是这样)。、 因为好不容易认识了C语言中所有的关键字(就是类型吧,像啥…...
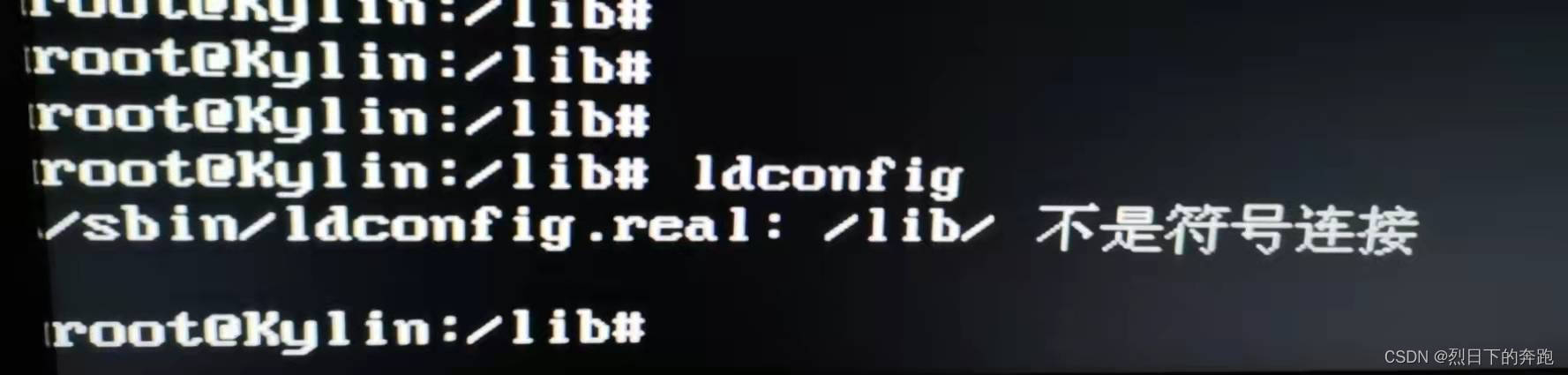
服务器系统启动卡logo问题解决分析
系统版本:Kylin-4.0.2-server-sp4-20200808.J1-57s-xxc_01-20210112-x86_64 问题:系统启动一直卡在麒麟logo那里,进不去系统。在gurb里去掉系统启动参数quiet和splash,发现启动卡在如下界面。 排查:开始怀疑是掉电导致…...
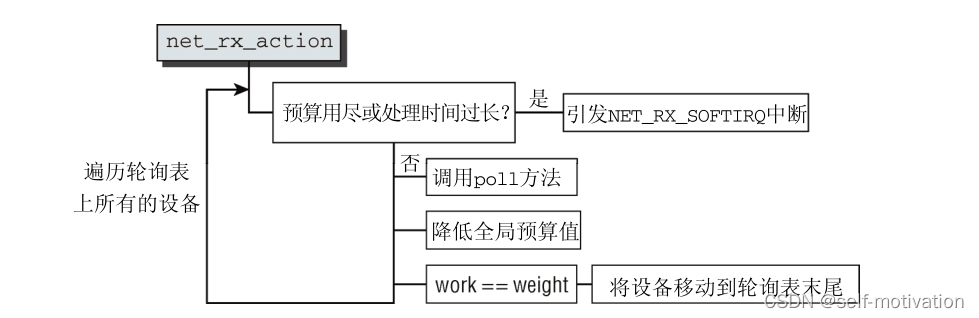
Linux NAPI ------------- epoll边缘触发模式
Linux处理网络数据包的一般流程 分组到达内核的时间是不可预测的。所有现代的设备驱动程序都使用中断来通知内核有分组到达。 网络驱动程序对特定于设备的中断设置了一个处理例程,因此每当该中断被引发时(即分组到达),内核都调用…...

使用poi-tl填充word模板,并转化为pdf输出
后端 依赖 <dependency><groupId>com.deepoove</groupId><artifactId>poi-tl</artifactId><version>1.12.0</version> </dependency>Word版本 Word版本填充代码 // 培训详情HashMap<String, Object> textMap new Ha…...

计算机视觉-机器学习-人工智能 顶会会议召开地址
计算机视觉-机器学习-人工智能 顶会会议召开地址 最近应该要整理中文资料的参考文献,很多会议文献都需要补全会议地点(新国标要求)。四处百度感觉也挺麻烦的,而且没有比较齐全的网站可以搜索。因此自己整理了一下计算机视觉-机器…...
GAN的原理分析与实例
为了便于理解,可以先玩一玩这个网站:GAN Lab: Play with Generative Adversarial Networks in Your Browser! GAN的本质:枯叶蝶和鸟。生成器的目标:让枯叶蝶进化,变得像枯叶,不被鸟准确识别。判别器的目标&…...
什么是POM设计模式?
为什么要用POM设计模式 前期,我们学会了使用PythonSelenium编写Web UI自动化测试线性脚本 线性脚本(以快递100网站登录举栗): import timefrom selenium import webdriver from selenium.webdriver.common.by import Bydriver …...
没有数据线,在手机上查看电脑备忘录怎么操作
在工作中,电脑和手机是我最常用的工具。我经常需要在电脑上记录一些重要的工作事项,然后又需要在手机上查看这些记录,以便随时了解工作进展。但是,每次都需要通过数据线来传输数据,实在是太麻烦了。 有一次࿰…...
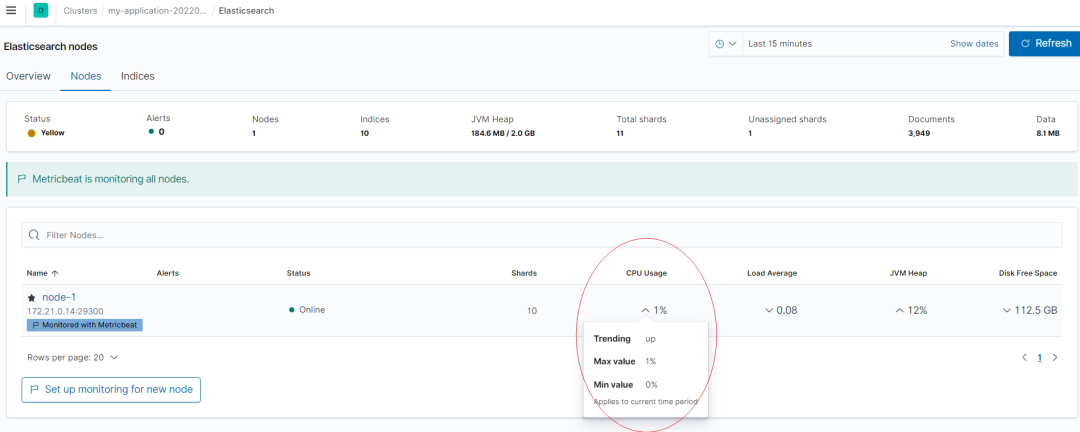
Elasitcsearch--解决CPU使用率升高
原文网址:Elasitcsearch--解决CPU使用率升高_IT利刃出鞘的博客-CSDN博客 简介 本文介绍如何解决ES导致的CPU使用率升高的问题。 问题描述 线上环境 Elasticsearch CPU 使用率飙升常见问题如下: Elasticsearch 使用线程池来管理并发操作的 CPU 资源。…...

vue和jQuery有什么区别
Vue 和 jQuery 是两种不同类型的前端工具,它们有一些显著的区别: Vue 响应式数据绑定:Vue 提供了双向数据绑定和响应式更新的能力,使得数据与视图之间的关系更加直观和易于维护。组件化开发:Vue 鼓励使用组件化的方式…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
