【模型量化】神经网络量化基础及代码学习总结
1 量化的介绍
量化是减少神经网络计算时间和能耗的最有效的方法之一。在神经网络量化中,权重和激活张量存储在比训练时通常使用的16-bit或32-bit更低的比特精度。当从32-bit降低到8-bit,存储张量的内存开销减少了4倍,矩阵乘法的计算成本则二次地减少了16倍。
神经网络已被证明对量化具有鲁棒性,这意味着它们可以被量化到较低的位宽,而对网络精度的影响相对较小。然而,神经网络的量化并不是自由的。低位宽量化会给网络带来噪声,从而导致精度的下降。虽然一些网络对这种噪声具有鲁棒性,但其他网络需要额外的工作来利用量化的好处。
量化实际上是将FLOAT32(32位浮点数)的参数量化到更低精度,精度的变化并不是简单的强制类型转换,而是为不同精度数据之间建立一种数据映射关系,最常见的就是定点与浮点之间的映射关系,使得以较小的精度损失代价得到较好的收益。
2 均匀仿射量化
均匀仿射量化也称为非对称量化,定义如下:
s s s:放缩因子(scale factor)/量化步长(step size),是浮点数
z z z:零点(zero-point),是整数,保证真实的0不会有量化误差,对ReLU和zero-padding很重要
b b b:位宽(bit-width),是整数,比如2, 4, 6, 8
s s s和 z z z的作用是将浮点数转化为整数,范围由b来定
1)将真实输入的浮点数 x \mathbb x x转化为无符号整数:
x i n t = c l a m p ( ⌊ x s ⌉ + z ; 0 , 2 b − 1 ) \mathbf{x}_{int} = \mathrm{clamp}(\lfloor\frac{\mathbf{x}}{s}\rceil+z; 0, 2^b-1) xint=clamp(⌊sx⌉+z;0,2b−1)
截断/四舍五入函数的定义:
c l a m p ( x ; a , c ) = { a , x < a , x , a ≤ x ≤ b , b , x > c . \mathrm{clamp}(x; a, c) = \begin{cases} a, x < a, \\ x, a \leq x\leq b,\\ b, x>c. \end{cases} clamp(x;a,c)=⎩ ⎨ ⎧a,x<a,x,a≤x≤b,b,x>c.
2)反量化(de-quantization)近似真实的输入 x \mathbf x x:
x ≈ x ^ = s ( x i n t − z ) \mathbf x\approx \mathbf{\hat x} =s(\mathbf x_{int} -z) x≈x^=s(xint−z)
结合以上1)2)步骤,得到如下量化函数的普遍定义:
x ^ = q ( x ; s , z , b ) = s ( c l a m p ( ⌊ x s ⌉ + z ; 0 , 2 b − 1 ) − z ) \mathbf{\hat x}=q(\mathbf x; s, z, b)=s(\mathrm{clamp}(\lfloor\frac{\mathbf{x}}{s}\rceil+z; 0, 2^b-1)-z) x^=q(x;s,z,b)=s(clamp(⌊sx⌉+z;0,2b−1)−z)
可以发现,量化函数包含了1)中的“浮点转整数”以及“反量化近似浮点”两个过程,这个过程通常被称为 伪量化(fake quantization)操作。
对伪量化的理解:把输入的浮点数据量化到整数,再反量化回 浮点数,以此来模拟量化误差,同时在反向传播的时候,采用Straight-Through-Estimator (STE)把导数回传到前面的层。
由上面的公式,有两个误差概念:
1) 截断误差(clipping error):浮点数 x x x超过量化范围时,会被截断,产生误差
2)舍入误差(rounding error):在做 ⌊ ⋅ ⌉ \lfloor \cdot\rceil ⌊⋅⌉时,会产生四舍五入的误差,误差范围在 [ − 1 2 , 1 2 ] [-\frac{1}{2}, \frac{1}{2}] [−21,21]
为了权衡两种误差,就需要设计合适的s和z,而它们依赖于量化范围和精度。
根据反量化过程,我们设 整数格 上的最大和最小值分别是 Q P = q m a x / s , Q N = q m i n / 2 Q_P=q_{max}/s, Q_N=q_{min}/2 QP=qmax/s,QN=qmin/2,量化值(浮点) 范围为 ( q m i n , q m a x ) (q_{min}, q_{max}) (qmin,qmax),其中 q m i n = s Q P = s ( 0 − z ) = − s z , q m a x = s Q N = s ( 2 b − 1 − z ) q_{min}=sQ_P=s(0-z)=-sz, q_{max}=sQ_N=s(2^b-1-z) qmin=sQP=s(0−z)=−sz,qmax=sQN=s(2b−1−z)。 x \mathbf x x超过这个范围会被截断,产生截断误差,如果希望减小截断误差,可以增大s的值,但是增大s会增大舍入误差,因为舍入误差的范围是 [ − 1 2 s , 1 2 s ] [-\frac{1}{2}s, \frac{1}{2}s] [−21s,21s]。
怎么计算放缩因子 s s s?
s = q m a x − q m i n 2 b − 1 . s=\frac{q_{max}-q_{min}}{2^b-1}. s=2b−1qmax−qmin.
2.1 对称均匀量化
对称均匀量化是上面非对称量化的简化版,限制了放缩因子 z = 0 z=0 z=0,但是偏移量的缺失限制了整数和浮点域之间的映射。
反量化(de-quantization)近似真实的输入 x \mathbf x x:
x ≈ x ^ = s x i n t x\approx \hat x =s\mathbf x_{int} x≈x^=sxint
将真实输入的浮点数 x \mathbb x x转化为无符号整数:
x i n t = c l a m p ( ⌊ x s ⌉ ; 0 , 2 b − 1 ) \mathbf{x}_{int} = \mathrm{clamp}(\lfloor\frac{\mathbf{x}}{s}\rceil; 0, 2^b-1) xint=clamp(⌊sx⌉;0,2b−1)
将真实输入的浮点数 x \mathbb x x转化为有符号整数:
x i n t = c l a m p ( ⌊ x s ⌉ ; − 2 b , 2 b − 1 ) \mathbf{x}_{int} = \mathrm{clamp}(\lfloor\frac{\mathbf{x}}{s}\rceil; -2^b, 2^b-1) xint=clamp(⌊sx⌉;−2b,2b−1)


坐标轴上方(蓝色)表示整数量化格,下方(黑色)表示浮点格。可以很清楚地看到,放缩因子 s s s就是量化的步长(step size), s x i n t s\mathbf x_{int} sxint是反量化近似真实浮点数。
2.2 Power-of-two量化(2的幂)
Power-of-two量化是对称量化的特例,放缩因子被限制到2的幂, s = 2 − k s=2^{-k} s=2−k,这对硬件是高效的,因为放缩 s s s相当于简单的比特移位操作(bit-shifting)。
2.3 量化的粒度
1)Per-tensor(张量粒度):神经网络中最常用,硬件实现简单,累加结果都用同样的放缩因子 s w s x s_ws_x swsx
2)Per-channel(通道粒度):更细粒度以提升模型性能,比如对于权重的不同输出通道采用不同的量化
3)Per-group(分组粒度)
3 量化模拟过程/伪量化
量化模拟:为了测试神经网络在量化设备上的运行效果,我们经常在用于训练神经网络的相同通用硬件上模拟量化行为。
我们的目的:使用浮点硬件来近似的定点运算。
优势:与在实际的量化硬件上实验或在使用量化的卷积核上实验相比,这种模拟明显更容易实现

(a)在设备推理过程中,对硬件的所有输入(偏置、权重和输入激活)都是定点格式
(b)然而,当我们使用通用的深度学习框架和通用硬件来模拟量化时,这些量都是以浮点格式表示的。这就是为什么我们在计算图中引入量化器块来诱导量化效应的原因
值得注意的是:
1)每个量化器都由一组量化参数(放缩因子、零点、位宽)来定义
2)量化器的输入和输出都是浮点格式,但输出都在量化网格上
3)每个量化器都由该公式计算: x ^ = q ( x ; s , z , b ) = s ( c l a m p ( ⌊ x s ⌉ + z ; 0 , 2 b − 1 ) − z ) \mathbf{\hat x}=q(\mathbf x; s, z, b)=s(\mathrm{clamp}(\lfloor\frac{\mathbf{x}}{s}\rceil+z; 0, 2^b-1)-z) x^=q(x;s,z,b)=s(clamp(⌊sx⌉+z;0,2b−1)−z),也就是包含了反量化过程
4)模拟量化实际上还是在浮点数上计算,模拟的其实是(截断与舍入)误差
4 基于STE的反向传播优化过程
严峻的优化问题:量化公式中中的round函数的梯度要么为零,要么到处都不定义,这使得基于梯度的训练不可能进行。一种解决方案就是采用straight-through estimator (STE)方法将round函数的梯度近似为1:
∂ ⌊ y ⌉ ∂ y = 1 \frac{\partial \lfloor y\rceil}{\partial y}=1 ∂y∂⌊y⌉=1
于是,量化的梯度就可求了,现对输入 x \mathbf x x进行求导:
∂ x ^ ∂ x = ∂ q ( x ) ∂ x = ∂ c l a m p ( ⌊ x s ⌉ ; Q N , Q P ) s ∂ x = { s ∂ Q N ∂ x = 0 , x < q m i n , s ∂ ⌊ x / s ⌉ ∂ x = s ∂ ⌊ x / s ⌉ ∂ ( x / s ) ∂ ( x / s ) ∂ x = s ⋅ 1 ⋅ 1 s = 1 , q m i n ≤ x ≤ q m a x , s ∂ Q P ∂ x = 0 , x > q m a x . = { 0 , x < q m i n , 1 , q m i n ≤ x ≤ q m a x , 0 , x > q m a x . \frac{\partial\mathbf{\hat x}}{\partial\mathbf x}=\frac{\partial q(\mathbf x)}{\partial\mathbf x}\\~~~~~~=\frac{\partial \mathrm{clamp}(\lfloor\frac{\mathbf x}{s}\rceil; Q_N, Q_P)s}{\partial\mathbf x}\\~~~~~~=\begin{cases} s\frac{\partial Q_N}{\partial \mathbf x}=0, \mathbf x < q_{min}, \\ s\frac{\partial \lfloor \mathbf x/s\rceil}{\partial \mathbf x}=s\frac{\partial \lfloor \mathbf x/s\rceil}{\partial (\mathbf x/s)}\frac{\partial (\mathbf x/s)}{\partial \mathbf x}=s\cdot 1\cdot \frac{1}{s}=1, q_{min} \leq x\leq q_{max},\\ s\frac{\partial Q_P}{\partial \mathbf x}=0, x>q_{max}. \end{cases}\\~~~~~~=\begin{cases} 0, \mathbf x < q_{min}, \\ 1, q_{min} \leq \mathbf x\leq q_{max},\\ 0, \mathbf x>q_{max}. \end{cases} ∂x∂x^=∂x∂q(x) =∂x∂clamp(⌊sx⌉;QN,QP)s =⎩ ⎨ ⎧s∂x∂QN=0,x<qmin,s∂x∂⌊x/s⌉=s∂(x/s)∂⌊x/s⌉∂x∂(x/s)=s⋅1⋅s1=1,qmin≤x≤qmax,s∂x∂QP=0,x>qmax. =⎩ ⎨ ⎧0,x<qmin,1,qmin≤x≤qmax,0,x>qmax.
也就是说,根据STE方法,当输入 x \mathbf x x在量化范围内时,其量化值对真实浮点值的梯度为1,反之为0。
对 s s s求导的数学推导过程如下文中LSQ工作所示。
下图展示了基于STE的反向传播过程,计算时有效跳过了量化器。

5 经典量化工作
Learned Step Size Quantization (ICLR 2020)
顾名思义,LSQ这篇文章就是在上述介绍的伪量化中引入可学习/训练的放缩因子 s s s。
设clamp的在 整数格 上的最大和最小值分别是 Q P = q m a x / s , Q N = q m i n / 2 Q_P=q_{max}/s, Q_N=q_{min}/2 QP=qmax/s,QN=qmin/2。
x ^ = s ( c l a m p ( ⌊ x s ⌉ ; Q N , Q P ) ) = { s Q N , x s < Q N , s ⌊ x s ⌉ , Q N ≤ x s ≤ Q P , s Q P , x s > Q P . \hat x=s(\mathrm{clamp}(\lfloor\frac{\mathbf{x}}{s}\rceil; Q_N, Q_P))\\~~~~=\begin{cases} sQ_N, \frac{\mathbf{x}}{s} < Q_N, \\ s\lfloor\frac{\mathbf{x}}{s}\rceil, Q_N \leq \frac{\mathbf{x}}{s}\leq Q_P,\\ sQ_P, \frac{\mathbf{x}}{s}>Q_P. \end{cases} x^=s(clamp(⌊sx⌉;QN,QP)) =⎩ ⎨ ⎧sQN,sx<QN,s⌊sx⌉,QN≤sx≤QP,sQP,sx>QP.
x ^ \mathbf{\hat x} x^对 s s s求导有:
∂ x ^ ∂ s = { Q N , x s < Q N , ⌊ x s ⌉ + s ∂ ⌊ x s ⌉ ∂ s , Q N ≤ x s ≤ Q P , Q P , x s > Q P . \frac{\partial\mathbf{\hat x}}{\partial s}=\begin{cases} Q_N, \frac{\mathbf{x}}{s} < Q_N, \\ \lfloor\frac{\mathbf{x}}{s}\rceil + s\frac{\partial\lfloor\frac{\mathbf{x}}{s}\rceil}{\partial s}, Q_N \leq \frac{\mathbf{x}}{s}\leq Q_P,\\ Q_P, \frac{\mathbf{x}}{s}>Q_P. \end{cases} ∂s∂x^=⎩ ⎨ ⎧QN,sx<QN,⌊sx⌉+s∂s∂⌊sx⌉,QN≤sx≤QP,QP,sx>QP.
其中, Q N , Q P , ⌊ x s ⌉ Q_N, Q_P, \lfloor\frac{\mathbf{x}}{s}\rceil QN,QP,⌊sx⌉都可以直接得到,但是 s ∂ ⌊ x s ⌉ ∂ s s\frac{\partial\lfloor\frac{\mathbf{x}}{s}\rceil}{\partial s} s∂s∂⌊sx⌉就不那么好算了。
根据STE,将round函数梯度近似为一个直通操作:
s ∂ ⌊ x s ⌉ ∂ s = s ∂ x s ∂ s = − s x s 2 = − x s s\frac{\partial\lfloor\frac{\mathbf{x}}{s}\rceil}{\partial s}=s\frac{\partial\frac{\mathbf{x}}{s}}{\partial s}=-s\frac{\mathbf x}{s^2}=-\frac{\mathbf x}{s} s∂s∂⌊sx⌉=s∂s∂sx=−ss2x=−sx
于是,得到LSQ原文中的导数值:
∂ x ^ ∂ s = { Q N , x s < Q N , ⌊ x s ⌉ − x s , Q N ≤ x s ≤ Q P , Q P , x s > Q P . \frac{\partial\mathbf{\hat x}}{\partial s}=\begin{cases} Q_N, \frac{\mathbf{x}}{s} < Q_N, \\ \lfloor\frac{\mathbf{x}}{s}\rceil - \frac{\mathbf x}{s}, Q_N \leq \frac{\mathbf{x}}{s}\leq Q_P,\\ Q_P, \frac{\mathbf{x}}{s}>Q_P. \end{cases} ∂s∂x^=⎩ ⎨ ⎧QN,sx<QN,⌊sx⌉−sx,QN≤sx≤QP,QP,sx>QP.
在LSQ中,每层的权重和激活值都有不同的 s s s,被初始化为 2 ⟨ ∣ x ∣ ⟩ Q P \frac{2\langle| \mathbf x|\rangle}{\sqrt{Q_P}} QP2⟨∣x∣⟩。
计算 s s s的梯度时,还需要兼顾模型权重的梯度,二者差异不能过大,LSQ定义了如下比例:
R = ∇ s L s / ∣ ∣ ∇ w L ∣ ∣ ∣ ∣ w ∣ ∣ → 1 R=\frac{\nabla_sL}{s}/\frac{||\nabla_wL||}{||w||}\rightarrow1 R=s∇sL/∣∣w∣∣∣∣∇wL∣∣→1。
为了保持训练的稳定,LSQ在 s s s的梯度上还乘了一个梯度缩放系数 g g g,对于权重, g = 1 / N W Q P g=1/\sqrt{N_WQ_P} g=1/NWQP,对于激活, g = 1 / N F Q P g=1/\sqrt{N_FQ_P} g=1/NFQP。其中, N W N_W NW是一层中的权重的大小, N F N_F NF是一层中的特征的大小。
代码实现
参考:LSQuantization复现
import torch
import torch.nn.functional as F
import math
from torch.autograd import Variableclass FunLSQ(torch.autograd.Function):@staticmethoddef forward(ctx, weight, alpha, g, Qn, Qp):assert alpha > 0, 'alpha = {}'.format(alpha)ctx.save_for_backward(weight, alpha)ctx.other = g, Qn, Qpq_w = (weight / alpha).round().clamp(Qn, Qp) # round+clamp将FP转化为intw_q = q_w * alpha # 乘scale重量化回FPreturn w_q@staticmethoddef backward(ctx, grad_weight):weight, alpha = ctx.saved_tensorsg, Qn, Qp = ctx.otherq_w = weight / alphaindicate_small = (q_w < Qn).float()indicate_big = (q_w > Qp).float()indicate_middle = torch.ones(indicate_small.shape).to(indicate_small.device) - indicate_small - indicate_biggrad_alpha = ((indicate_small * Qn + indicate_big * Qp + indicate_middle * (-q_w + q_w.round())) * grad_weight * g).sum().unsqueeze(dim=0) # 计算s梯度时的判断语句grad_weight = indicate_middle * grad_weightreturn grad_weight, grad_alpha, None, None, Nonenbits = 4
Qn = -2 ** (nbits - 1)
Qp = 2 ** (nbits - 1) - 1
g = 1.0 / 2
2 LSQ+: Improving low-bit quantization through learnable offsets and better initialization (CVPR 2020)
LSQ+和LSQ非常相似,就放在一起讲了。LSQ在LSQ+的基础上,引入了可学习的offset,也就是零点 z z z,其定义如下:
x i n t = c l a m p ( ⌊ x − β s ⌉ ; Q N , Q P ) \mathbf x_{int}=\mathrm{clamp}(\lfloor\frac{\mathbf{x-\beta}}{s}\rceil; Q_N, Q_P) xint=clamp(⌊sx−β⌉;QN,QP)
x ^ = s x i n t + β \mathbf{\hat x}=s\mathbf x_{int}+\beta x^=sxint+β
然后按照LSQ的方式对 s , β s,\beta s,β求偏导数进行优化。
3 XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks
算是非常早期将二值(1-bit)表示引入神经网络的文章了,本文提出两种近似:
1)Binary-Weight-Network:只有权重是1-bit
对于输入 I \mathbf I I,我们用二值滤波器 B ∈ { + 1 , − 1 } \mathbf B\in \{+1, -1\} B∈{+1,−1}和一个放缩因子 α \alpha α来近似真实浮点滤波器 W \mathbf W W: W ≈ α B \mathbf W\approx \alpha \mathbf B W≈αB,于是卷积的计算可以近似为:
I ∗ W ≈ ( I ⊕ B ) α \mathbf I*\mathbf W\approx (\mathbf I\oplus \mathbf B)\alpha I∗W≈(I⊕B)α
如何优化二值权重?我们的目标是找到 W = α B \mathbf W=\alpha \mathbf B W=αB的最优估计,解决如下优化问题:
J ( B , α ) = ∣ ∣ W − α B ∣ ∣ 2 α ∗ , B ∗ = a r g m i n α , B J ( B , α ) J(\mathbf B, \alpha)=||\mathbf W-\alpha \mathbf B||^2~~~~\alpha^*, \mathbf B^*=\mathrm{argmin_{\alpha, \mathbf B}}J(\mathbf B, \alpha) J(B,α)=∣∣W−αB∣∣2 α∗,B∗=argminα,BJ(B,α)
展开后得到:

其中, B ⊤ B , W ⊤ W \mathbf B^\top \mathbf B, \mathbf W^\top \mathbf W B⊤B,W⊤W都是常数,因此优化目标集中在第二项 W ⊤ B \mathbf W^\top \mathbf B W⊤B上:

这个优化问题的解可以是使 B = + 1 ( W ≥ 0 ) , B = − 1 ( W < 0 ) \mathbf B=+1(\mathbf W\geq 0), \mathbf B=-1(\mathbf W< 0) B=+1(W≥0),B=−1(W<0),原因是这样可以保持 W ⊤ B \mathbf W^\top \mathbf B W⊤B取最大值+1。因此,可以得到 B ∗ = s i g n ( W ) \mathbf B^*=\mathrm{sign}(\mathbf W) B∗=sign(W)。
然后,求解放缩因子 α \alpha α的最优解,我们用 J J J对 α \alpha α求偏导数:
∂ J ∂ α = 2 α B ⊤ B − 2 W ⊤ B \frac{\partial J}{\partial \alpha}=2\alpha\mathbf B^\top\mathbf B-2\mathbf W^\top \mathbf B ∂α∂J=2αB⊤B−2W⊤B
当偏导数等于0时,可求解:
α ∗ = W ⊤ B B ⊤ B = W ⊤ B n \alpha^*=\frac{\mathbf W^\top \mathbf B}{\mathbf B^\top \mathbf B}=\frac{\mathbf W^\top \mathbf B}{n} α∗=B⊤BW⊤B=nW⊤B
其中,令 n = B ⊤ B n=\mathbf B^\top \mathbf B n=B⊤B,此时的 B \mathbf B B代入 B ∗ \mathbf B^* B∗,于是:
α ∗ = W ⊤ B n = W ⊤ s i g n ( W ) n = ∑ ∣ W ∣ n = 1 n ∣ ∣ W ∣ ∣ 1 \alpha^*=\frac{\mathbf W^\top \mathbf B}{n}=\frac{\mathbf W^\top \mathrm{sign}(\mathbf W)}{n}=\frac{\sum |\mathbf W|}{n}=\frac{1}{n}||\mathbf W||_1 α∗=nW⊤B=nW⊤sign(W)=n∑∣W∣=n1∣∣W∣∣1
其中, ∣ ∣ ⋅ ∣ ∣ 1 ||\cdot||_1 ∣∣⋅∣∣1表示 ℓ 1 \ell_1 ℓ1-norm,即对矩阵中的所有元素的绝对值求和。
总结
二值权重/滤波器的最优估计是权重的符号函数值,放缩因子的最优估计是权重的绝对值平均值。

训练过程
需要注意的是,反向传播计算梯度用的近似的权重 W ~ \tilde W W~,而真正被更新的权重应该是真实的高精度权重 W W W。

2)XNOR-Networks:权重和激活值都是1-bit,乘法全部简化为异或计算
二值dot product计算
X ⊤ W ≈ β H ⊤ α B \mathbf X^\top W\approx \beta \mathbf H^\top \alpha \mathbf B X⊤W≈βH⊤αB,其中, H , B ∈ { − 1 , + 1 } , β , α ∈ R + \mathbf H, \mathbf B\in \{-1, +1\}, \beta, \alpha\in\mathbb R^+ H,B∈{−1,+1},β,α∈R+,优化目标如下:

令 Y = X W , C ∈ { − 1 , + 1 } , C = H B , γ = α β \mathbf Y=\mathbf X \mathbf W, \mathbf C\in \{-1, +1\}, \mathbf C=\mathbf H \mathbf B, \gamma=\alpha\beta Y=XW,C∈{−1,+1},C=HB,γ=αβ,于是优化目标简化为:

根据Binary-Weight-Network,通过符号函数可以求解最优的二值激活值和权重:

同理,根据,通过 ℓ 1 \ell_1 ℓ1-norm可以求解最优的放缩因子:

二值卷积计算
对于输入 I \mathbf I I,首先计算 A = ∑ ∣ I : , : , i ∣ c \mathbf A=\frac{\sum |\mathbf I_{:, :, i}|}{c} A=c∑∣I:,:,i∣,其中 c c c是输入通道数,这个过程计算了跨通道的输入 I \mathbf I I中元素的绝对值的平均值。然后将 I \mathbf I I和一个2D滤波器 k ∈ R w × h \mathbf k\in \mathbb R^{w\times h} k∈Rw×h做卷积, K = A ∗ k , k i j = 1 w h \mathbf K=\mathbf A * \mathbf k, \mathbf k_{ij}=\frac{1}{wh} K=A∗k,kij=wh1。 K \mathbf K K中包含了 I \mathbf I I中左右子张量的放缩因子 β \beta β。
于是,卷积的近似计算如下:

其中, ⊛ \circledast ⊛表示XNOR+bitcount操作。

代码参考:XNOR-Net-PyTorch
符号函数直接通过sign函数实现:
input = input.sign()
参考资料
- 量化训练之可微量化参数—LSQ
- A White Paper on Neural Network Quantization
相关文章:

【模型量化】神经网络量化基础及代码学习总结
1 量化的介绍 量化是减少神经网络计算时间和能耗的最有效的方法之一。在神经网络量化中,权重和激活张量存储在比训练时通常使用的16-bit或32-bit更低的比特精度。当从32-bit降低到8-bit,存储张量的内存开销减少了4倍,矩阵乘法的计算成本则二…...

次模和K次模是多项式可解吗?
次模是多项式可解吗 **是的,**次模函数的最优化问题通常是多项式时间可解的。这是因为次模性质导致了问题的结构,使得可以利用高效的算法进行求解。 具体来说,针对次模函数的最优化问题,例如极大化或极小化这样的目标函数…...
网络安全——SQL注入实验
一、实验目的要求: 二、实验设备与环境: 三、实验原理: 四、实验步骤: 五、实验现象、结果记录及整理: 六、分析讨论与思考题解答: 七、实验截图: 一、实验目的要求: 1、…...

【cocotb】【达坦科技DatenLord】Cocotb Workshop分享
https://www.bilibili.com/video/BV19e4y1k7EE/?spm_id_from333.337.search-card.all.click&vd_sourcefd0f4be6d0a5aaa0a79d89604df3154a 方便RFM实现 cocotb_test 替代makefile , 类似python 函数执行...

Kafka系列之:统计kafka集群Topic的分区数和副本数,批量增加topic副本数
Kafka系列之:统计kafka集群Topic的分区数和副本数,批量增加topic副本数 一、创建KafkaAdminClient二、获取kafka集群topic元信息三、获取每个topic的名称、分区数、副本数四、生成增加topic副本的json文件五、执行增加topic副本的命令六、确认topic增加副本是否成功一、创建K…...

开具实习证明:在线实习项目介绍
大数据在线实习项目,是在线上为学生提供实习经验的项目。我们希望能够帮助想要在毕业后从事数据科学类工作的学生更加顺利地适应从教室到职场的转换;也帮助那些在工作中需要处理数据、实现数据价值的其他职能的从业者高效快速地掌握每天都能用起来的数据…...
MFC逆向之CrackMe Level3 过反调试 + 写注册机
今天我来分享一下,过反调试的方法以及使用IDA还原代码 写注册机的过程 由于内容太多,我准备分为两个帖子写,这个帖子主要是写IDA还原代码,下一个帖子是写反调试的分析以及过反调试和异常 这个CrackMe Level3是一个朋友发我的,我也不知道他在哪里弄的,我感觉挺好玩的,对反调试…...

【Centos】
一、Virtualbox安装Centos 1、Virtualbox 下载地址: Virtualbox 2、Centos 下载地址: Centos 3、Virtualbox安装Centos教程 Virtualbox安装Centos教程: Virtualbox安装Centos教程...

1+X大数据平台运维职业技能等级证书中级
hadoop: 由于我的功能限制,我无法直接为您执行这些操作或提供实际的截图。但我可以为您提供一步步的指导,帮助您完成这些任务。 1. 解压JDK安装包到“/usr/local/src”路径,并配置环境变量。 - 解压JDK:tar -zxf jd…...
网络基础(五):网络层协议介绍
目录 一、网络层 1、网络层的概念 2、网络层功能 3、IP数据包格式 二、ICMP协议 1、ICMP的作用和功能 2、ping命令的使用 2.1ping命令的通用格式 2.2ping命令的常用参数 2.3TypeCode:查看不同功能的ICMP报文 2.4ping出现问题 3、Tracert 4、冲突域 5、…...
浅显易懂 @JsonIgnore 的作用
1.JsonIgnore作用 在json序列化/反序列化时将java bean中使用了该注解的属性忽略掉 2.这个注解可以用在类/属性上 例如:在返回user对象时,在pwd属性上使用这个注解,返回user对象时会直接去掉pwd这个字段,不管这个属性有没…...

【计算机设计大赛作品】诗意千年—唐朝诗人群像的数字展现_附源码—信息可视化赛道获奖项目深入剖析【可视化项目案例-20】
🎉🎊🎉 你的技术旅程将在这里启航! 记得看本专栏里顶置的可视化宝典导航贴哦! 🚀🚀 本专栏为可视化专栏,包含现有的所有可视化技术。订阅专栏用户在文章底部可下载对应案例完整源码以供大家深入的学习研究。 🎓 每一个案例都会提供完整代码和详细的讲解,不论你…...
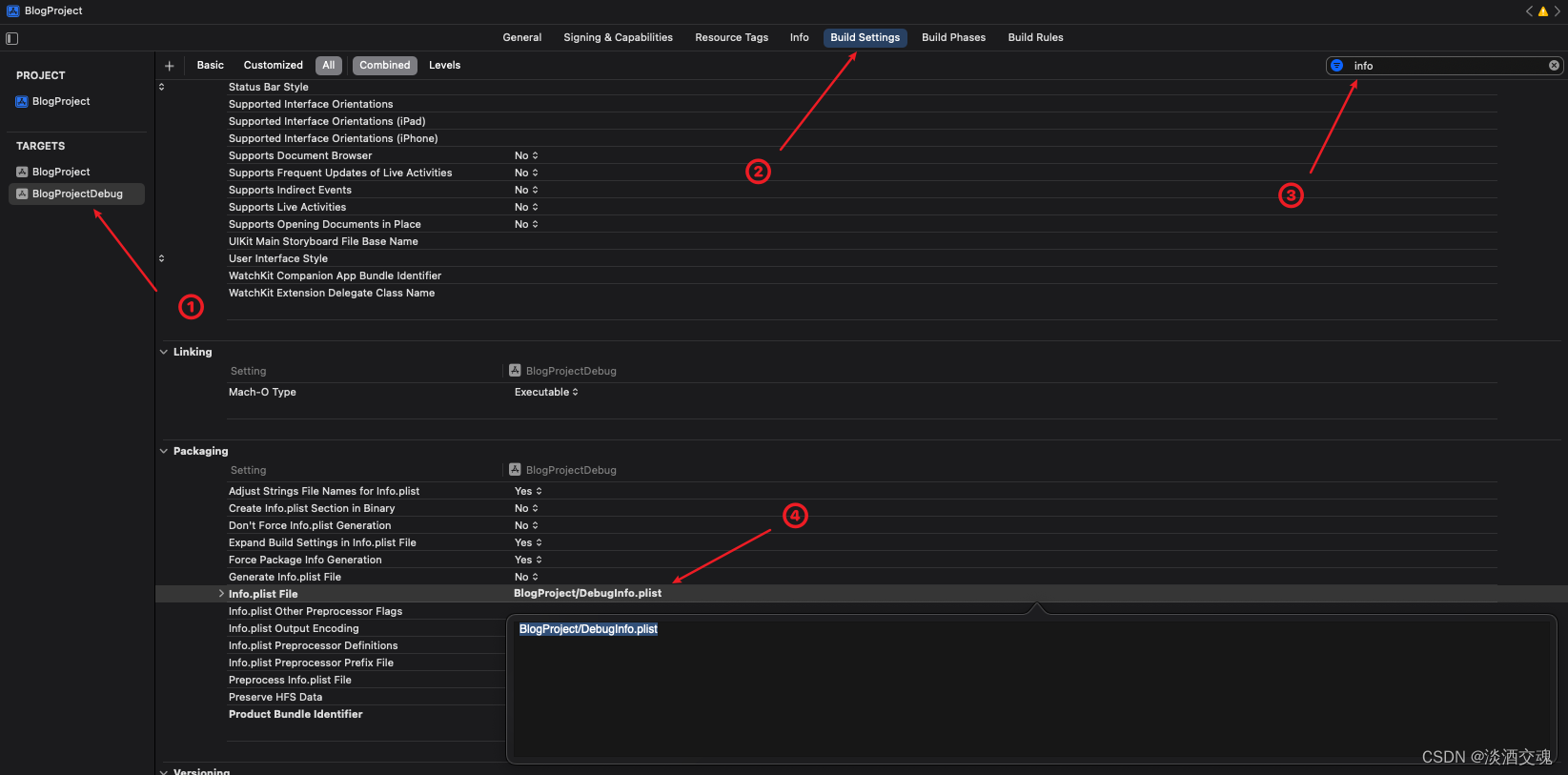
「Swift」Xcode多Target创建
前言:我们日常开发中会使用多个环境,如Dev、UAT,每个环境对应的业务功能都不同,但每个环境之间都只存在较小的差异,所以此时可以使用创建多个Target来实现,每个Target对应这个一个App,可以实现一…...

Python文件命名规则:批量重命名与规则匹配的文件
我从一个旧的 iOS 项目中获得了一个文件夹,其中包含许多类似于 image.png image2x.png another-image.png another-image2x.png然而,由于该项目现在只需要 2x.png 图像,我已经删除了所有的文件没有 2x 的名称。 但是我现在想知道如何轻松…...

『npm』一条命令快速配置npm淘宝国内镜像
📣读完这篇文章里你能收获到 一条命令快速切换至淘宝镜像恢复官方镜像 文章目录 一、设置淘宝镜像源二、恢复官方镜像源三、查看当前使用的镜像 一、设置淘宝镜像源 npm config set registry https://registry.npm.taobao.org服务器建议全局设置 sudo npm config…...
Java EE 多线程之线程安全的集合类
文章目录 1. 多线程环境使用 ArrayList1. 1 Collections.synchronizedList(new ArrayList)1.2 CopyOnWriteArrayList 2. 多线程环境使用队列2.1 ArrayBlockingQueue2.2 LinkedBlockingQueue2.3 PriorityBlockingQueue2.4 TransferQueue 3. 多线程环境使用哈希表3.1 Hashtable3.…...

明明随机数
明明想在学校中请一些同学一起做一项问卷调查,为了实验的客观性,他先用计算机生成了N个1到1000之间的随机整数(N<100),对于其中重复的数字,只保留一个,把其余相同的数去掉,不同的数对应着不同的学生的学…...

优思学院|如何建立公司运营指标体系?如何推行六西格玛改进运营指标?
关键绩效指标 (KPI) 是测量您团队或组织朝重要商业目标进展表现如何的量化指标,组织会在多个层面使用 KPI,这视乎您想要追踪何指标而定,您可以设定全组织的、特定团队的、或甚至是个人 KPI。 良好的KPI能让公司管理者掌握组织的营运是否进度…...
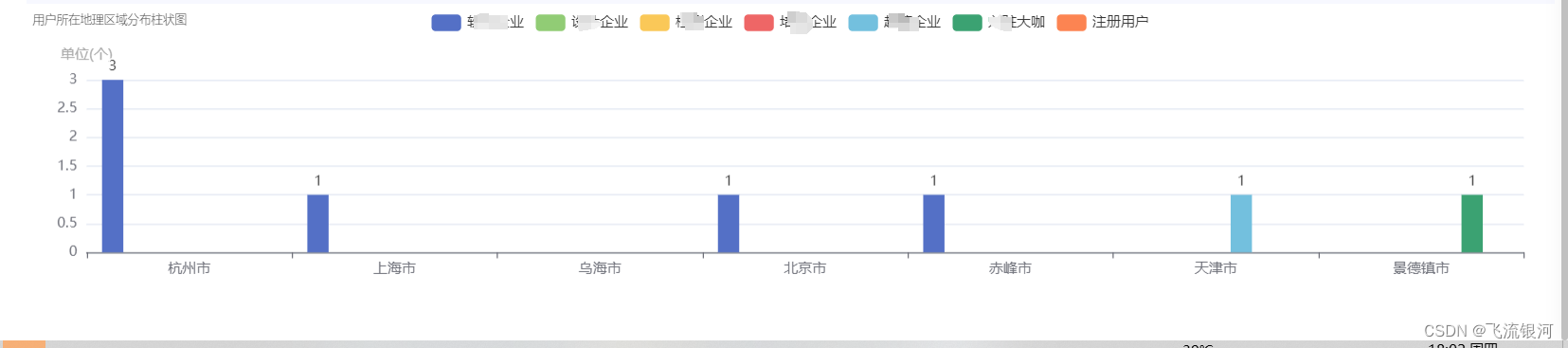
vue2 echarts不同角色多个类型数据的柱状图
前端代码: 先按照echarts插件。在页面里引用 import * as echarts from "echarts";设置div <div style"width:100%;height:250px;margin-top: 4px;" id"addressChart"></div>方法: addressEcharts() {const option {g…...

Mysql表的数据类型
数据类型 https://www.sjkjc.com/mysql/varchar/ MySQL 中的数据类型包括以下几个大类: 字符串类型 数字类型 日期和时间类型 二进制类型 地理位置数据类型 JSON 数据类型 MySQL 字符串数据类型 VARCHAR:纯文本字符串,字符串长度是可变的…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
