Python卡尔曼滤波器OpenCV跟踪和预测物体的轨迹
模拟简单物体二维运动和预测位置
预测数学式
想象一下你正坐在一辆汽车里,在雾中行驶。 你几乎看不到路,但你有一个 GPS 系统可以告诉你你的速度和位置。 问题是,这个 GPS 并不完美; 它有时会产生噪音或不准确的读数。 您如何知道您的实际位置以及行驶速度?
卡尔曼滤波器提供了答案。它结合了:
- 系统(您的汽车)根据其模型预测什么(称为预测步骤)。
- 它接收到的噪声测量结果(在这个类比中是 GPS 读数)产生的估计值在统计上比预测或测量本身更可靠。
卡尔曼滤波器主要有两个步骤:
预测:
x ′ = A x + B u P ′ = A P k − 1 A T + Q \begin{aligned} x^{\prime} & =A x+B u \\ P^{\prime} & =A P_{k-1} A^T+Q \end{aligned} x′P′=Ax+Bu=APk−1AT+Q
- x ′ x^{\prime} x′是预测状态。
- A A A是状态转换模型。
- B B B是控制输入模型。
- u u u是控制向量。
- P ′ P^{\prime} P′是预测估计协方差。
- Q Q Q是过程噪声协方差。
更新:
y = z − H x S = H P ′ H T + R K = P ′ H T S − 1 x = x ′ + K y P = ( I − K H ) P ′ \begin{aligned} y & =z-H x \\ S & =H P^{\prime} H^T+R \\ K & =P^{\prime} H^T S^{-1} \\ x & =x^{\prime}+K y \\ P & =(I-K H) P^{\prime} \end{aligned} ySKxP=z−Hx=HP′HT+R=P′HTS−1=x′+Ky=(I−KH)P′
- y y y是残值
- z z z是测量值
- H H H是观测模型
- S S S是协方差
- R R R是测量噪声协方差
- K K K是卡尔曼增益
- x x x是是更新后的状态估计
- P P P是是更新后的估计协方差
代码处理
安装OpenCV和Matplotlib。
使用 OpenCV 实现卡尔曼滤波器
OpenCV 提供了一个方便的 KalmanFilter 类,让我们可以实现卡尔曼滤波器,而不必陷入数学细节的困境。 在本演示中,我们将模拟对象的简单 2D 运动并使用卡尔曼滤波器来估计其位置。
让我们首先初始化 2D 运动的卡尔曼滤波器。
# Initialize the Kalman filter
kalman_2d = cv2.KalmanFilter(4, 2)
kalman_2d.measurementMatrix = np.array([[1, 0, 0, 0], [0, 1, 0, 0]], np.float32)
kalman_2d.transitionMatrix = np.array([[1, 0, 1, 0], [0, 1, 0, 1], [0, 0, 1, 0], [0, 0, 0, 1]], np.float32)
kalman_2d.processNoiseCov = np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]], np.float32) * 1e-4
代码释义:
- 我们系统的状态由 4x1 矩阵表示: [ x , y , x ˙ , y ˙ ] [x, y, \dot{x}, \dot{y}] [x,y,x˙,y˙] ,其中 x x x 和 y y y 是二维坐标,并且 x ˙ \dot{x} x˙ 和 y ˙ \dot{y} y˙ 分别表示 x 和 y 方向的速度。
- measurementMatrix 将状态与测量联系起来。在我们的例子中,我们只测量位置,而不测量速度.。
- TransitionMatrix 表示状态转换模型。为简单起见,我们假设速度恒定。
- processNoiseCov 代表与我们的流程相关的噪声。
模拟物体运动和可视化
我们将模拟一个沿直线移动的物体,并在其测量中添加一些噪声。当物体移动时,我们将应用卡尔曼滤波器来估计其真实位置。
- 我们有 200 个预测状态,每个状态都用一个矩阵表示。
- 我们还有 200 个噪声测量,每个都由一个2*1 矩阵表示。
让我们可视化对象的真实路径、噪声测量值以及卡尔曼滤波器估计的路径。
fig, ax = plt.subplots(figsize=(10, 6))
ax.set_xlim(0, 4 * np.pi)
ax.set_ylim(-1.5, 1.5)
ax.set_title("Kalman Filter in 2D Motion Estimation")
ax.set_xlabel("X Position")
ax.set_ylabel("Y Position")# Plotting the true path, noisy measurements, and Kalman filter estimations
ax.plot(true_path[:, 0], true_path[:, 1], 'g-', label="True Path")
ax.scatter(np.array(measurements)[:, 0], np.array(measurements)[:, 1], c='red', s=20, label="Noisy Measurements")
ax.plot(np.array(predictions)[:, 0, 0], np.array(predictions)[:, 1, 0], 'b-', label="Kalman Filter Estimation")
ax.legend()
plt.show()
代码释义:
- **True Path:**这是对象所采取的实际路径(尽管我们在现实场景中没有这个路径)。
- **Noisy Measurements:**这些是我们从传感器获得的读数,这些读数被噪声破坏了。
- **Kalman Filter Estimations:**这些是卡尔曼滤波器估计的位置,理想情况下应该接近真实路径。
这是我们模拟的 2D 运动的可视化:
预测真实物体的轨迹
跟踪视频人物
二维对象跟踪
源代码
参阅一 - 亚图跨际
参阅二 - 亚图跨际
相关文章:

Python卡尔曼滤波器OpenCV跟踪和预测物体的轨迹
模拟简单物体二维运动和预测位置 预测数学式 想象一下你正坐在一辆汽车里,在雾中行驶。 你几乎看不到路,但你有一个 GPS 系统可以告诉你你的速度和位置。 问题是,这个 GPS 并不完美; 它有时会产生噪音或不准确的读数。 您如何知…...

LeetCode Hot100 25.K个一组翻转链表
题目: 给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。 k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。 你不能只是单纯…...

中职网络安全应急响应—Server2228
应急响应 任务环境说明: 服务器场景:Server2228(开放链接) 用户名:root,密码:p@ssw0rd123 1. 找出被黑客修改的系统别名,并将倒数第二个别名作为Flag值提交; 通过用户名和密码登录系统 在 Linux 中,利用 “alias” 命令去查看当前系统中定义的所有别名 flag:ss …...

springboot 获取路径
PostConstructpublic void setup() {try {// jar包所在目录 /Users/mashanshanString path this.getClass().getProtectionDomain().getCodeSource().getLocation().getPath();System.out.println("path:" path); // file:/Users/mashanshan/manual-admin-0.0.1-…...

C#上位机与欧姆龙PLC的通信01----项目背景
最近,【西门庆】作为项目经理负责一个70万的北京项目,需要在工控系统集成软件开发中和欧 姆龙PLC对接,考虑项目现场情况优先想到了采用FinsTCP通讯协议,接下来就是记录如何一步步实现这些通讯过程的,希望给电气工程师&…...

SE考研真题总结(二)
接上条,今天继续更新~ SE考研真题总结(一)-CSDN博客文章浏览阅读340次,点赞6次,收藏11次。本帖开始分享考研真题中设计【软件工程】的部分,预计会出5期左右,敬请期待~https://blog.csdn.net/js…...
vue中预览pdf的方法
使用vue-pdf 备注:这里只介绍了一页的pdf <div class"animation-box-pdf"><pdf :src"http://xxxx" /> </div>import Pdf from vue-pdf // src可以是文件地址url,也可以是文件流blob(将blob转成url&a…...

详谈前端中常用的加/密算法
本文主要详细介绍了在前端开发中常用的加/解密算法,以及前端如何实现。 总的来说:前端加密无论使用哪个加密都一样是有可能性被他人获取到相关的公钥或密钥的(比如:拦截请求、查看源代码等),然后进行加密与…...

宣布全面推出适用于 macOS 的 Amazon EC2 M2 Pro Mac 实例
即日起,Amazon Elastic Compute Cloud (Amazon EC2) M2 Pro Mac 实例现已全面推出 (GA)。在为 Apple 平台(例如 iOS、macOS、iPadOS、tvOS、watchOS、visionOS 和 Safari)构建和测试应用程序时,这些实例的性能比现有的 M1 Mac 实例…...

【记录版】SpringBoot下Filter注册源码解读
SpringBoot TomcatEmbeddedContext Servlet ApplicationFilterChain Filter 背景: 在之前博客中有说明SpringBoot内嵌Web容器后,Filter及Servlet解析与注册流程的变化。将Filter实例封装成FilterRegistrationBean实例并添加到ServletContext后&…...

WPF的WebBrowser控件
在 WPF 中显示网页,你可以使用 WebBrowser 控件来实现。WebBrowser 控件是一个嵌入式的浏览器控件,可以加载和显示网页内容。 以下是在 WPF 中显示网页的示例代码: <Window x:Class"WpfApp.MainWindow"xmlns"http://sche…...
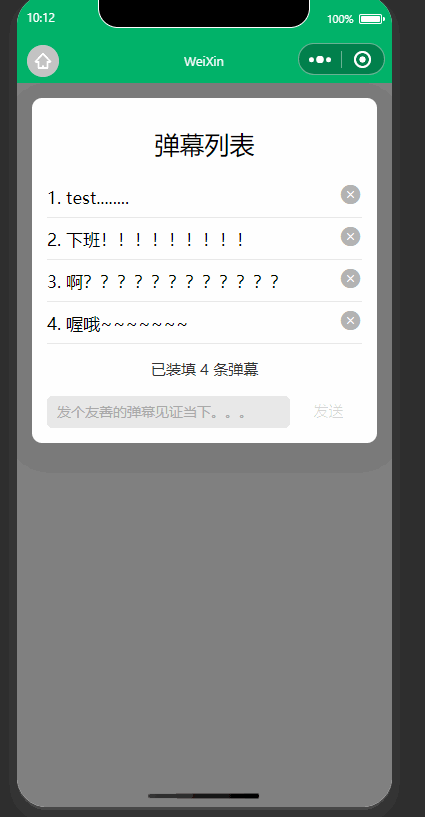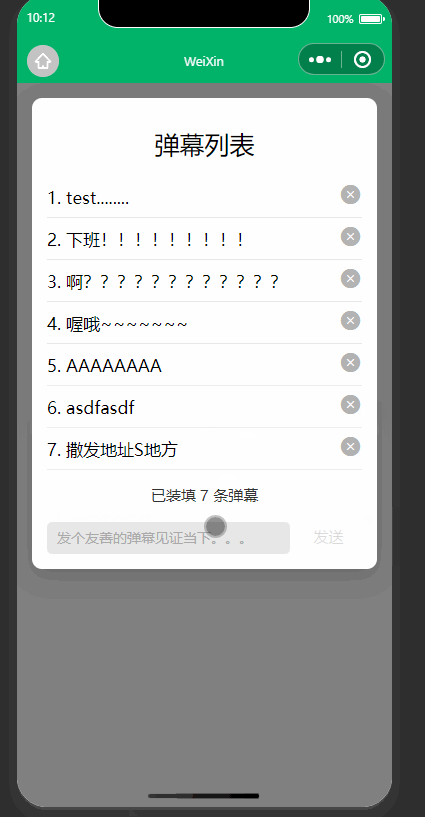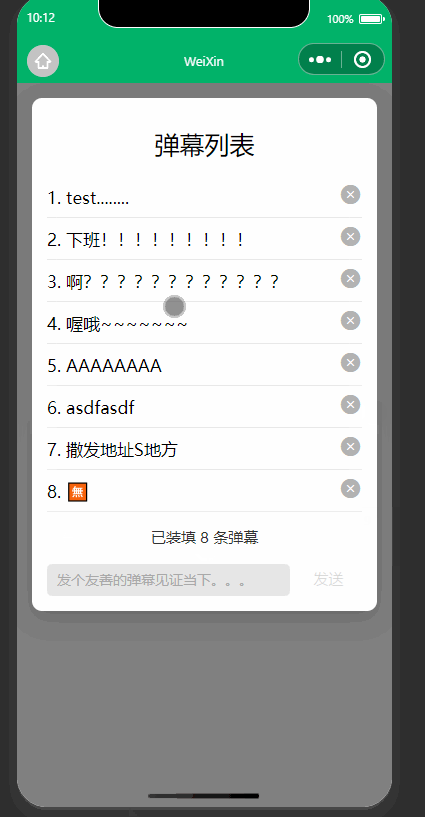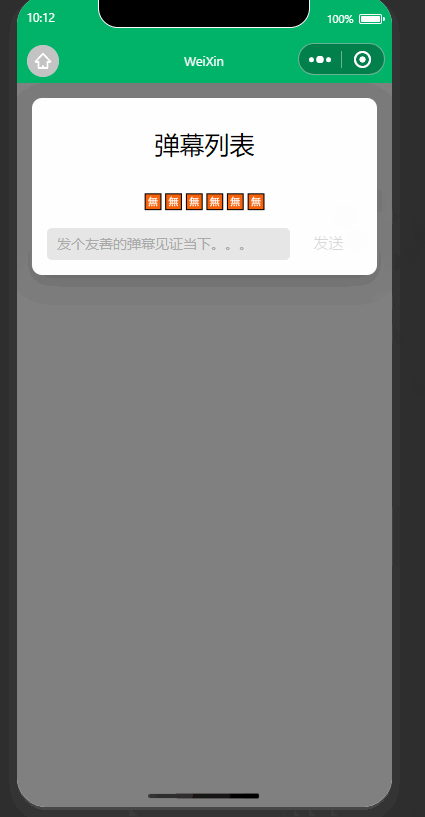
WX小程序案例(一):弹幕列表
WXML内容 <!--pages/formCase/formCase.wxml--> <!-- <text>pages/formCase/formCase.wxml</text> --> <view class"bk bkimg"><!-- <image src"/static/imgs/ceeb653ely1g9na2k0k6ug206o06oaa8.gif" mode"scal…...
基于ssm医用物理学实验考核系统论文
摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本医用物理学实验考核系统就是在这样的大环境下诞生,其可以帮助管理者在短时间内处理完毕庞大的数…...
鸿蒙HarmonyOS4.0 入门与实战
一、开发准备: 熟悉鸿蒙官网安装DevEco Studio熟悉鸿蒙官网 HarmonyOS应用开发官网 - 华为HarmonyOS打造全场景新服务 应用设计相关资源: 开发相关资源: 例如开发工具 DevEco Studio 的下载 应用发布: 开发文档:...
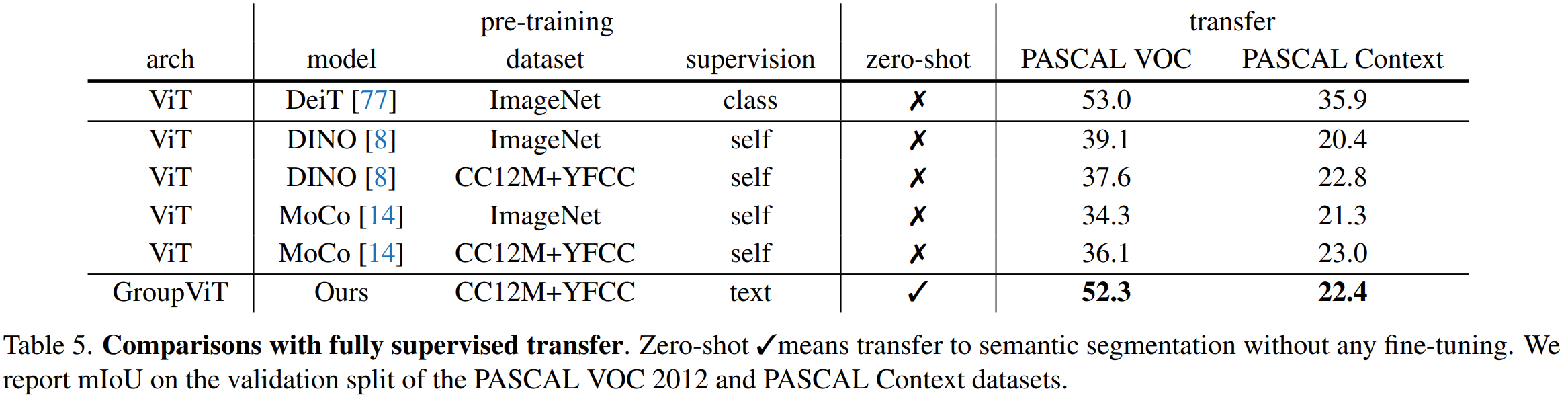
论文阅读——GroupViT
GroupViT: Semantic Segmentation Emerges from Text Supervision 一、思想 把Transformer层分为多个组阶段grouping stages,每个stage通过自注意力机制学习一组tokens,然后使用学习到的组tokens通过分组模块Grouping Block融合相似的图片tokens。通过这…...

时光机器:用rrweb打造可回溯的用户体验!
在现代Web应用中,理解用户如何与你的产品互动变得越来越重要。rrweb(record and replay the web)是一个开源库,它能够记录用户在网站上的所有操作,并能够像回放视频一样回放这些操作。这就像给你的网站装上了一台时光机…...

不同的葡萄品种的葡萄酒有什么共同特质?
在某种程度上几乎所有的葡萄酒都是混合的,在大多数葡萄酒产地,法律允许在单一品种葡萄酒中混入高达15%的另一种葡萄酒,且还能被称为由主要葡萄酿造的单一品种葡萄酒酒。这些单一品种葡萄酒混合了少量其他葡萄酒,是为了创造一个特质…...

Visual Studio编辑器中C4996 ‘scanf‘: This function or variable may be unsafe.问题解决方案
目录 编辑 题目:简单的ab 1. 题目描述 2. 输入格式 3. 输出格式 4. 样例输入 5. 样例输出 6. 解题思路 7. 代码示例 8. 报错解决 方案一 方案二 方案三 方案四 总结 题目:简单的ab 1. 题目描述 输入两个整数a和b,…...
C与C++编程语言的区别和联系
一、引言 C和C是两种广泛使用的编程语言,它们都在软件开发领域有着广泛的应用。虽然C是从C语言演化而来的,但两者之间存在一些重要的区别和联系。本文将详细介绍这两种编程语言的相同点和不同点,并通过实际例子进行说明。 二、C与C的相同点 …...

UE4 UMG 颜色字体和PS对应关系
与PS中对应的是Hex sRGB色号 但是PS中采用的16进制色号为6位 UE4中的为8位 UMG制作时默认dpi为96像素/英寸,psd默认dpi是72像素/英寸。 在GUI设计时将dpi设为96,或者将72dpi下字体的字号乘以0.75,都能还原效果图中的效果。...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
