【贪心】LeetCode-406. 根据身高重建队列
406. 根据身高重建队列。
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
示例 2:
输入:people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出:[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]
提示:
1 <= people.length <= 2000
0 <= hi <= 10^6
0 <= ki < people.length
题目数据确保队列可以被重建
算法分析
解题思路
- 先排序,h升序,k降序
- 根据k值站位
class Solution {public int[][] reconstructQueue(int[][] people) {//h升序,k降序Arrays.sort(people, (o1,o2) -> o1[0] != o2[0] ? o2[0]- o1[0] : o1[1] - o2[1]);List<int[]> ans = new ArrayList<int[]>();for (int[] person : people) {ans.add(person[1], person);}return ans.toArray(new int[ans.size()][]);}
}
复杂性分析
时间复杂度:O(n2)
空间复杂度:O(logn)
相关文章:

【贪心】LeetCode-406. 根据身高重建队列
406. 根据身高重建队列。 假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。 请你重新…...
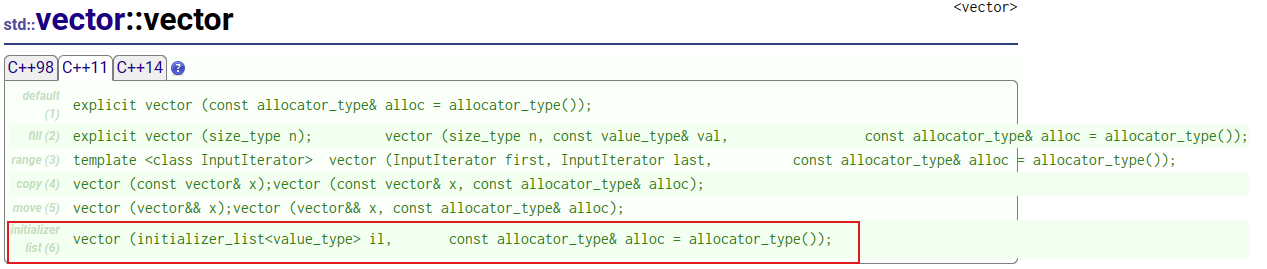
【C++11特性篇】C++11中新增的initializer_list——初始化的小利器
前言 大家好吖,欢迎来到 YY 滴C11系列 ,热烈欢迎! 本章主要内容面向接触过C的老铁 主要内容含: 欢迎订阅 YY滴C专栏!更多干货持续更新!以下是传送门! 目录 一.探究std::initializer_list是什么…...

springboot(ssm宠物美容机构CRM系统 宠物服务商城系统Java系统
springboot(ssm宠物美容机构CRM系统 客户关系管理系统Java系统 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或8.0ÿ…...

LSTM 双向 Bi-LSTM
目录 一.Bi-LSTM介绍 二.Bi-LSTM结构 Bi-LSTM 代码实例 一.Bi-LSTM介绍 由于LSTM只能从序列里由前往后预测,为了既能够从前往后预测,也能从后往前预测,Bi-LSTM便被发明了出来。简单来说,BiLSTM就是由前向LSTM与后向LSTM组合而成。 二.Bi-LSTM结构 转自:...

2024测试开发面试题完整版本(附答案)
目录 1. 什么是软件测试, 谈谈你对软件测试的了解 2. 我看你简历上有写了解常见的开发模型和测试模型, 那你跟我讲一下敏捷模型 3. 我看你简历上还写了挺多开发技能的, 那你给我讲讲哈希表的实现流程 4. 谈一谈什么是线程安全问题, 如何解决 5. 既然你选择走测…...
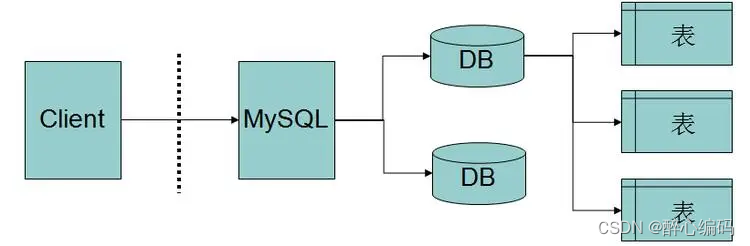
MySQL作为服务端的配置过程与实际案例
MySQL是一款流行的关系型数据库管理系统,广泛应用于各种业务场景中。作为服务端,MySQL的配置过程对于数据库的性能、安全性和稳定性至关重要。本文将详细介绍MySQL作为服务端的配置过程,并通过一个实际案例进行举例说明。 一、MySQL服务端配…...

Appium 自动化自学篇 —— 初识Appium自动化!
Appium 简介 随着移动终端的普及,手机应用越来越多,也越来越重要。而作为测试 的我们也要与时俱进,努力学习手机 App 的相关测试,文章将介绍手机自动化测试框架 Appium 。 那究竟什么是 Appium 呢? 接下来我们一起来学习PythonS…...
Linux基本操作指令
哈喽小伙伴们,从这篇文章开始,在学习数据结构的同时,我们开启一个新的篇章——Linux操作系统的学习,这将会是又一个新的开始,希望小伙伴们能够认真细心,不要掉队哦。 目录 一.什么是Linux 二.为什么要学习…...

探索SD-WAN技术对传统制造业实现智能制造的作用
在智能制造背景下,传统制造业面临着日益增长的信息化建设需求。随着企业趋向数字化转型,构建稳定、高效的网络基础设施成为提升企业核心竞争力的重要一环。 制造业企业信息化建设中的组网需求: 第一,连接多地分支机构,…...

C++基础-this指针详解
本文详细讲解C++this指针 定义 this 是 C++ 中的一个关键字,一个特殊的指针,它指向当前对象地址(换句话说,其值为 &object),通过它可以访问当前对象的所有成员。 类定义好后我们就可以通过类来创建多个实例对象,每个对象都有各自的实例属性(实例变量),但是非内…...
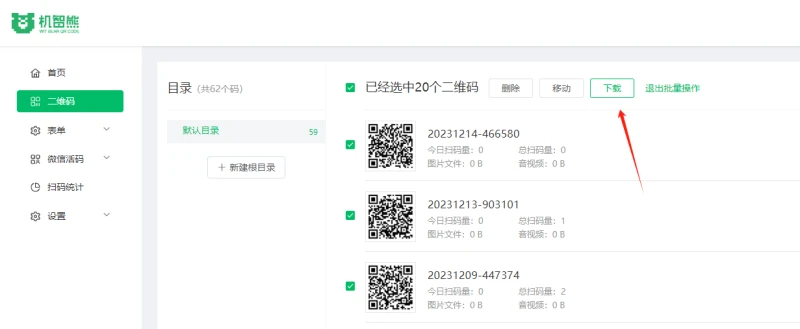
如何一键生成多个文件二维码?批量文件二维码制作技巧
文件能批量生成二维码吗?现在的二维码用途范围越来越广,比如常见的有图文、文件、问卷、音频或者视频等内容生成二维码图片,扫码查看内容。那么当需要将很多的文件每个都单独生成一个二维码时,有没有比较简单快捷的操作方法吗&…...

SQL连续
SQL连续 1、连续概述2、SQL连续及应用2.1、静态连续2.2、动态连续1、连续概述 连续问题是实际数据开发中比较常见的场景。例如,统计用户连续活跃天数等 SQL如何解决连续问题?本文主要介绍连续性问题,重点以常见的连续活跃场景为例,抽象出通用的连续问题解决方案。连续问题…...

sql server导出与导入
解决:不同版本sql server复制表、导数据;把数据库的结构和全部数据从2016版导入到2014版。 分离数据为mdf,ldf后,导入过程中无权限、被占用问题。 文章目录 使用脚本(.sql文件)导出导入备注 使用mdf,mlf导…...
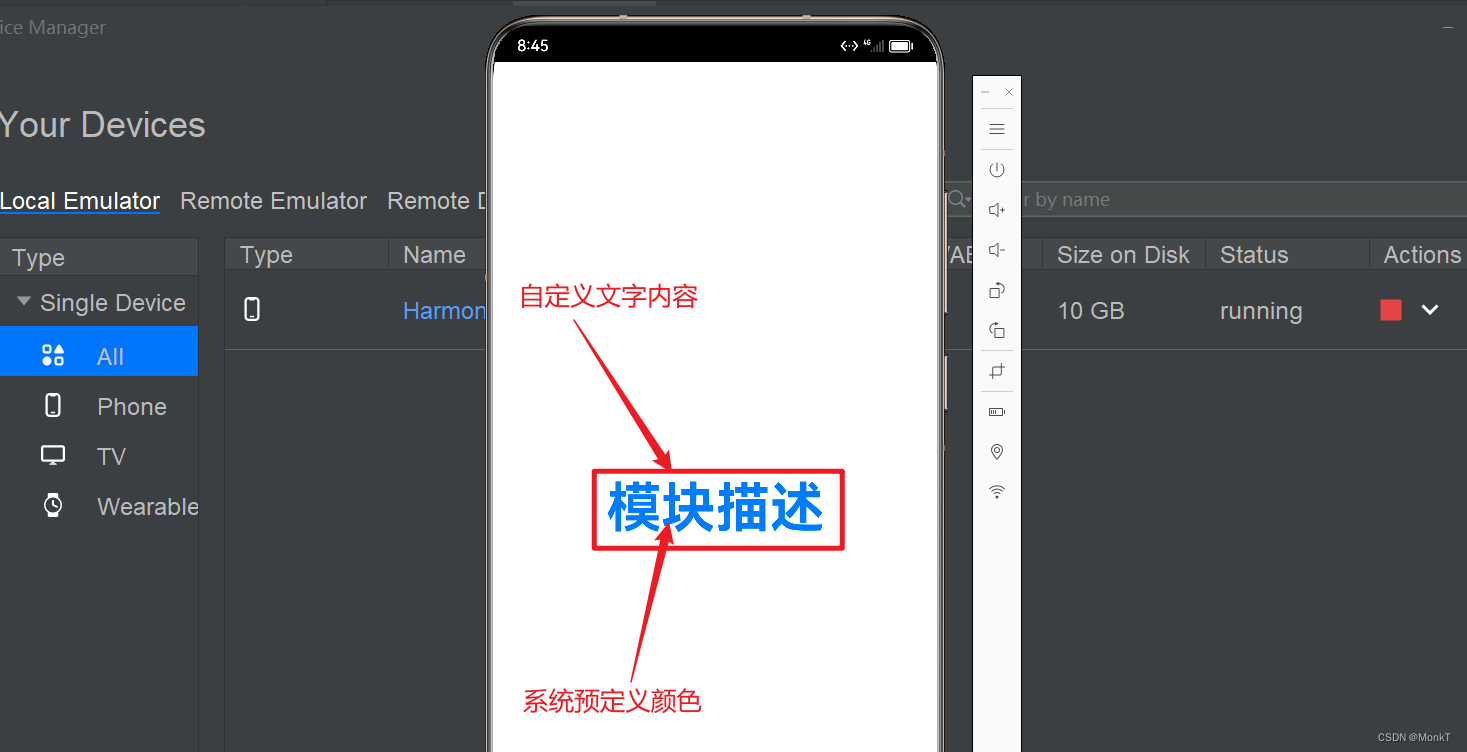
DevEco Studio 项目鸿蒙(HarmonyOS)资源引用(自定统和系统)
DevEco Studio 项目鸿蒙(HarmonyOS)资源引用(自定统和系统) 一、操作环境 操作系统: Windows 10 专业版 IDE:DevEco Studio 3.1 SDK:HarmonyOS 3.1 二、资源访问 HarmonyOS应用资源分为两类,一类是应用资源&…...

使用国内镜像源安装opencv
在控制台输入命令: pip install opencv-python -i https://pypi.tuna.tsinghua.edu.cn/simple 验证安装: step 1: 打开终端;step 2: 输入python,进入Python编译环境;step 3: 粘贴…...
人工智能与大数据的紧密联系
随着科技的飞速发展,人工智能(Artificial Intelligence,AI)和大数据(Big Data)已成为当今社会的热门话题。人工智能在许多领域的应用越来越广泛,而大数据则提供了支持和驱动AI技术的巨大资源。本…...

macbookpro 2024怎么恢复出厂设置
可能你的MacBook曾经是高性能的代表,但是现在它正慢慢地逝去了自己的光芒?随着逐年的使用以及文件的添加和程序的安装,你的MacBook可能会开始变得迟缓卡顿,或者失却了以往的光彩。如果你发现你的Mac开始出现这些严重问题ÿ…...

Linux系统编程(二):标准 I/O 库(下)
参考引用 UNIX 环境高级编程 (第3版)嵌入式Linux C应用编程-正点原子 1. 标准 I/O 库简介 标准 I/O 库是指:标准 C 库中用于文件 I/O 操作(如:读、写文件等)相关的一系列库函数的集合 标准 I/O 库函数相关的函数定义都在头文件 &…...
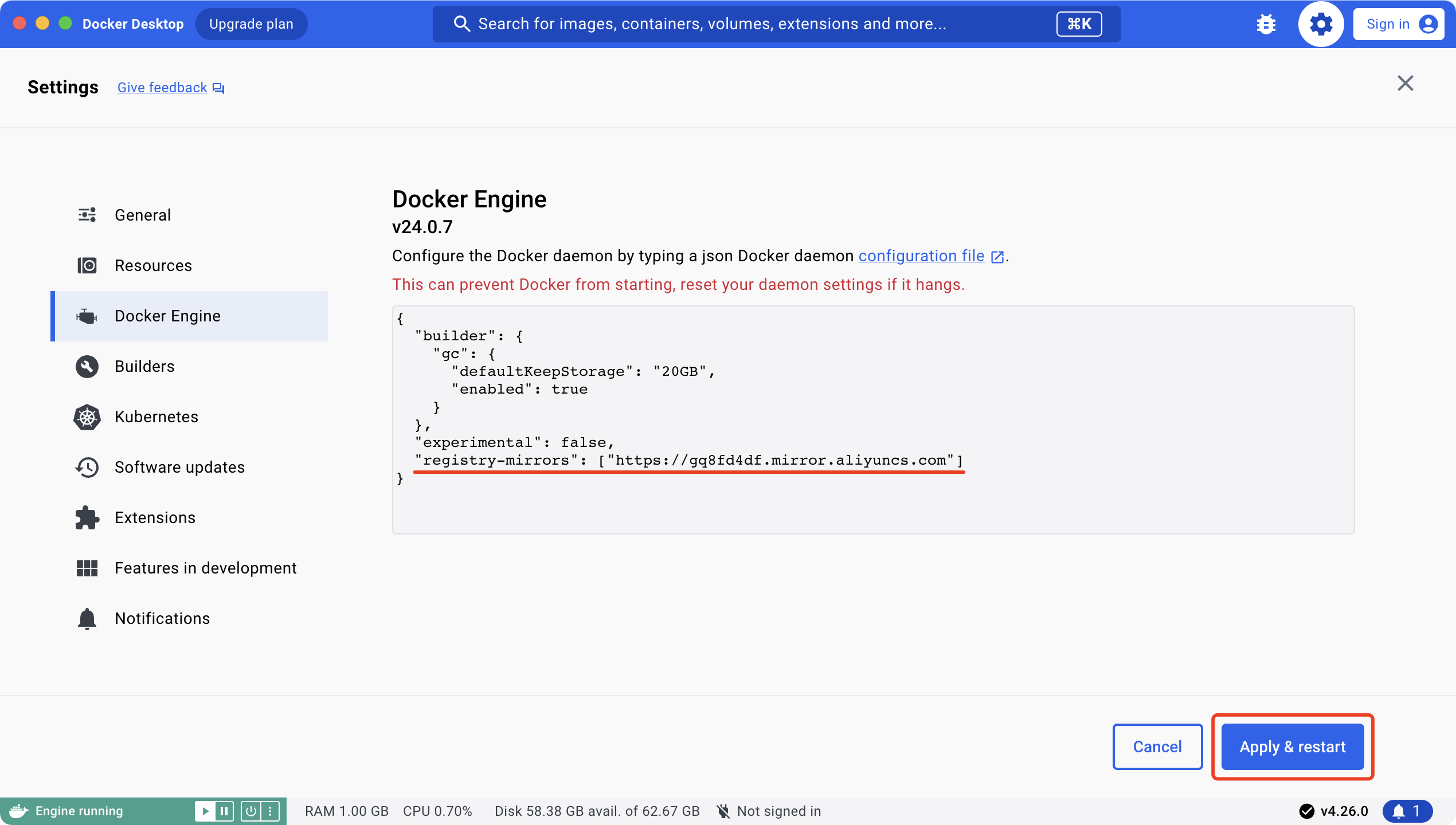
Mr. Cappuccino的第65杯咖啡——MacOS安装Docker
MacOS安装Docker 下载Docker安装Docker查看Docker相关信息镜像加速 下载Docker Docker官网 Docker文档中心 Docker桌面版下载地址 安装Docker 查看Docker相关信息 docker --versiondocker info镜像加速 阿里云镜像加速器 "registry-mirrors": ["https://gq8…...
)
解决 Docker Hub 国内无法访问的方法(Docker 镜像下载加速)
参考文章: 知乎:解决目前Docker Hub国内无法访问方法汇总 docker配置 修改配置文件 vim /etc/docker/daemon.json配置内容如下: {"builder": {"gc": {"defaultKeepStorage": "20GB","enab…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...
