matlab - 特殊矩阵、矩阵求值、稀疏矩阵
学习视频
1.特殊矩阵
1.1 通用特殊矩阵
format
% 零矩阵(全0) 幺矩阵(全1) 单位矩阵
% zeros ones eye rand(生成0~1的随机元素) randn(生成均值为1,方差为0的符合正太分布的随机阵)zeros(3) % 3x3的全0方阵
zeros(3, 4) % 3x4的全0矩阵
exA = ones(3, 5) % 3x5的全1矩阵
zeros(size(exA)) % 和exA大小一致的全0矩阵eye(3, 3), eye(5, 3) % 主对角线为1的全0矩阵

示例:


1.2 用于特殊领域的矩阵
魔方矩阵(magic)

范德蒙矩阵(vander)

希尔伯特矩阵(hilb)

2. 矩阵变换
2.1 基础概念
对角阵(diag)
主对角线有值,其他均为0的矩阵
diag作用1 - 创建对角阵:


diag作用2 - 取对角线:

数量矩阵(k*eye)
只有主对角线有值,且全相同

单位矩阵(eye)
只有主对角线有值,且全是1

三角阵

秩(rank)
非零子式的最高阶数就是秩
设在矩阵 A中有一个不等于0的r阶子式D,且所有r+1阶子式(如果存在的话)全等于0,那么D称为矩阵A的最高阶非零子式,数r称为矩阵A的秩,记作R(A).并规定零矩阵的秩等于0.
-是否可逆:只有满秩的矩阵才可逆
-初等变换后矩阵的秩不变
-判断非齐次线性方程组(方程组右侧的值不全为0)解的情况

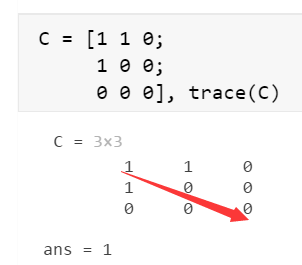
迹(trace)
矩阵主对角线元素的和,trace()计算;相似变换时矩阵的迹不变
逆(inv)和广义逆(pinv)
设A是数域上的一个n阶方阵,若在相同数域上存在另一个n阶矩B,使得:
AB=BA=I
则我们称B是A的逆矩阵,而A则被称为可逆矩阵。

示例:

伪逆:对于非方阵、奇异阵(是方阵,但是行列式为0)、非满秩矩阵(rank(A) ~= n)是不存在逆矩阵的;但是可以去定义一个伪逆矩阵pinv()。

行列式
矩阵行列式是指矩阵的全部元素构成的行列式。排成 n 阶方阵形式的 n^2 个数所确定的一个数称为 n 阶方阵 A 的行列式,记为:det(A) 或 |A|
一个 2x2 的矩阵的行列式可表示为:

范数(norm)
简单来说,用来度量某个向量空间(或矩阵)中的每个向量的长度或大小。
条件数(cond)
矩阵A的条件数等于A的范数与A的逆的范数的乘积,即cond(A)=‖A‖·‖A^(-1)‖,是判断矩阵病态与否的一种度量,条件数越大矩阵越病态。(条件数同时描述了矩阵 A 对向量的拉伸能力和压缩能力,换句话说,令向量发生形变的能力。条件数越大,向量在变换后越可能变化得越多。)
示例:

2.2 矩阵的转置与旋转
转置(.')

共轭转置(')

旋转(rot90(A, k))

左右翻转(fliplr)

上下翻转(flipud)

3.矩阵求值
3.1行列式求值(det)

3.2 矩阵的秩与迹

3.3向量和矩阵的范数


3.4 矩阵的条件数

4.矩阵特征值与特征向量(eig)


5.稀疏矩阵
5.1区分稀疏矩阵(含极大量0元素的矩阵) 和 采用稀疏方式存储的矩阵

5.2稀疏存储方式的产生(sparse)

5.3与稀疏矩阵操作相关的函数
find()

full()

spconvert()

spdiags()

5.4稀疏矩阵应用实例


相关文章:

matlab - 特殊矩阵、矩阵求值、稀疏矩阵
学习视频1.特殊矩阵1.1 通用特殊矩阵format % 零矩阵(全0) 幺矩阵(全1) 单位矩阵 % zeros ones eye rand(生成0~1的随机元素) randn(生成均值为1,方差为0的符合正太分布的随机阵)zeros(3) % 3x3的全0方阵 zeros(3, 4) % 3x4的全0矩阵 exA ones(3, 5) % 3x5的…...
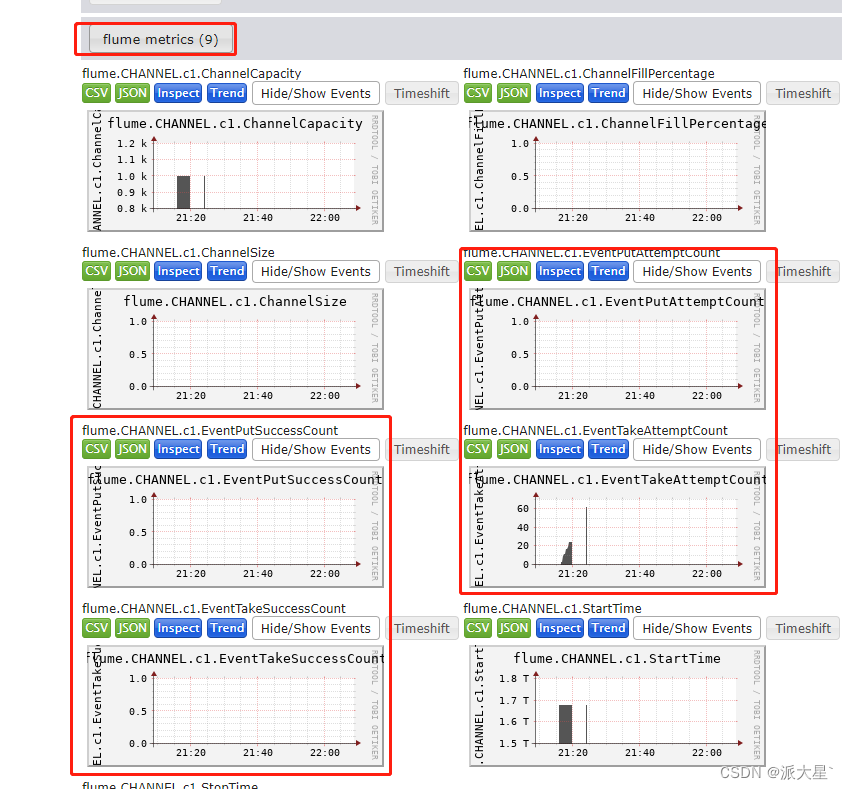
Flume使用入门
目录 一. Flume简单介绍 1. Agent 2. Source 3. Sink 4. Channel 5. Event 二. 环境安装 1. 创建日志目录 2. 修改日志配置文件 3.修改运行堆内存 4. 确定日志打印的位置 5. 修改flume使用内存 内存调大 三. 校验flume 1. 安装netcat工具和net-tools工具 2. 判…...
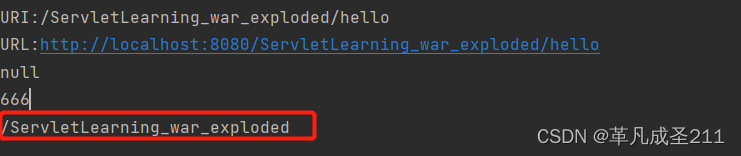
【Servlet篇2】Servlet的工作过程,Servlet的api——HttpServletRequest
一、Servlet的工作过程 二、Tomcat的初始化 步骤1:寻找到当前目录下面所有需要加载的Servlet(也就是类) 步骤2:根据类加载的结果创建实例(通过反射),并且放入集合当中 步骤3:实例创建好之后,调用Servlet的init()方…...

【JAVASE】注解
文章目录1.概述2.JDK内置注解2.1override注解2.2 Deprecated注解3.元注解4.注解中定义属性4.1 属性value4.2 属性是一个数组5. 反射注解6.注解在开发中的作用1.概述 注解,也叫注释,是一种引用数据类型。编译后也同样生成class字节码文件。 语法 [修饰…...
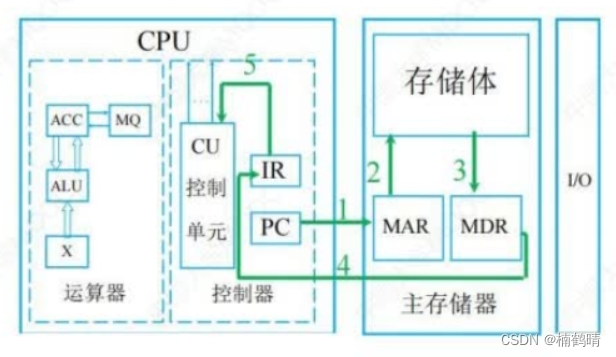
【408之计算机组成原理】计算机系统概述
目录前言一、计算机的发展历程1. 计算机发展的四代变化2. 计算机元件的更新换代3. 计算机软件的发展二、计算机系统层次结构1. 计算机系统的组成2. 冯诺依曼体系结构3. 计算机的功能部件1. 输入设备2. 输出设备3. 存储器4. 运算器5. 控制器三、 分析计算机各个部件在执行代码中…...
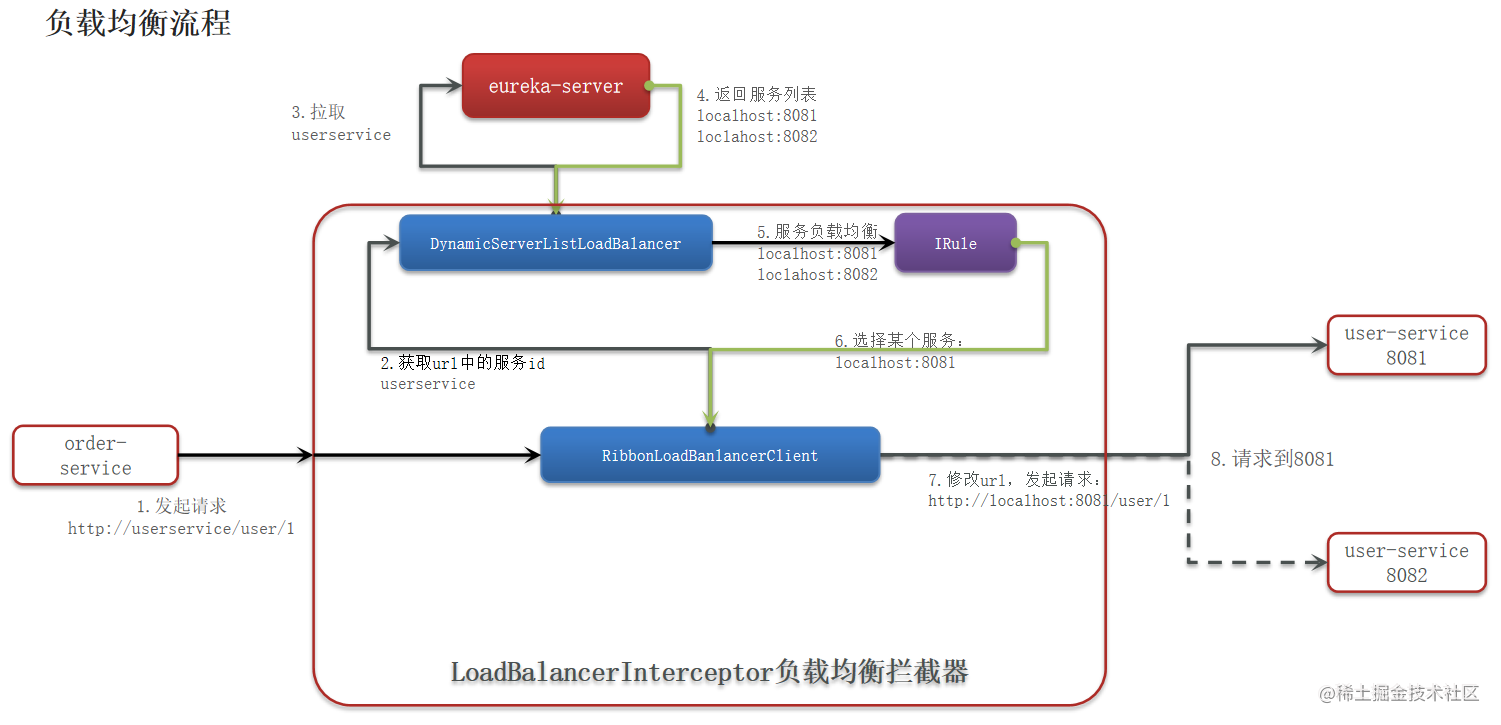
1.Spring Cloud (Hoxton.SR10) 学习笔记—基础知识
本文目录如下:一、Spring Cloud基础知识什么是微服务架构?服务拆分 有哪些注意事项?什么是分布式集群?分布式的 CAP 原则?组件 - Spring Cloud 哪几个组件比较重要?组件 - 为什么要使用这些组件?组件 - Na…...

嵌入式开发工具箱【持续更新中】【VMware、Ubuntutftp、nfs、SecureCRT、XShell、Source Insight 4.0】
一、概述 本文主要介绍嵌入式开发过程中需要用到的工具及简单的使用方法。避免在搭建嵌入式开发环境时,需要四处寻找文档,收藏此文章,一文搞定。 大多数嵌入式开发环境是使用Linux作为目标开发系统,所以开发主机一般都是Linux系统…...

深究Java Hibernate框架下的Deserialization
写在前面 Hibernate是一个开源免费的、基于 ORM 技术的 Java 持久化框架。通俗地说,Hibernate 是一个用来连接和操作数据库的 Java 框架,它最大的优点是使用了 ORM 技术。 Hibernate 支持几乎所有主流的关系型数据库,只要在配置文件中设置好…...
微服务一 实用篇 - Docker安装
《微服务一 实用篇 - Docker安装》 提示: 本材料只做个人学习参考,不作为系统的学习流程,请注意识别!!! 《微服务一 实用篇 - Docker安装》《微服务一 实用篇 - Docker安装》0.安装Docker1.CentOS安装Docker1.1.卸载(可选)1.2.安装docker1.3.启动docker…...

JavaSE22-集合2-map
文章目录一、集合概念二、map集合1、Map集合的特点2、HashMap2.1 HashMap特点2.2 创建对象2.3 常用方法2.4 遍历2.4.1 使用entrySet遍历2.4.2 使用keySet遍历3、HashMap的key去重原理一、集合概念 集合就是用于存储多个数据的容器。相对于具有相同功能的数组来说,集…...
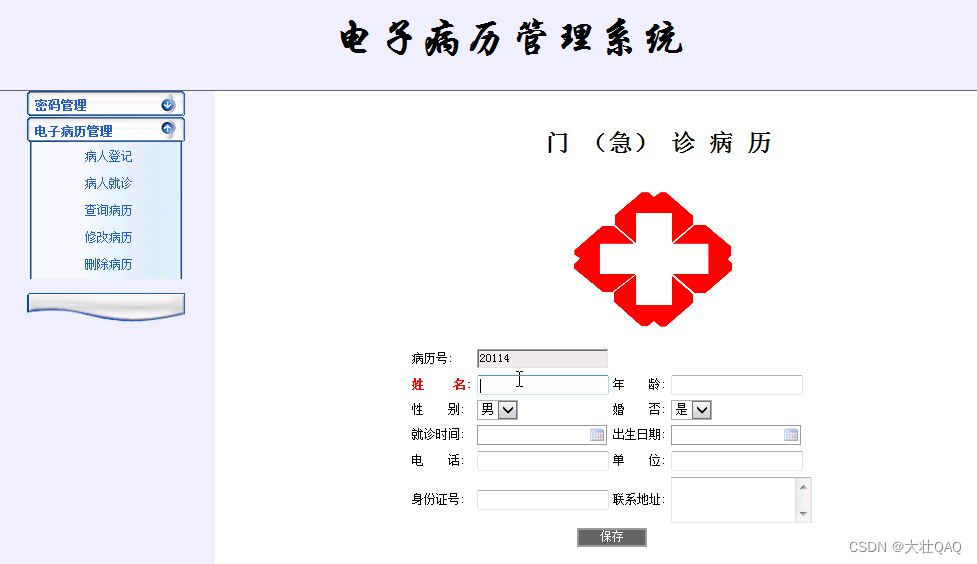
【项目精选】病历管理系统设计与实现(源码+视频)
点击下载源码 企业财务管理系统主要用于电子病历来提高医院各项工作的效率和质量,促进医学科研、教学;减轻各类事务性工作的劳动强度,使他们腾出更多的精力和时间来服务于病人。本系统结构如下: 电子病例系统: 病人登…...
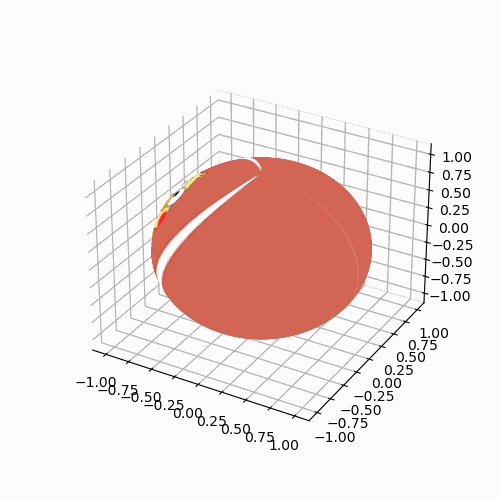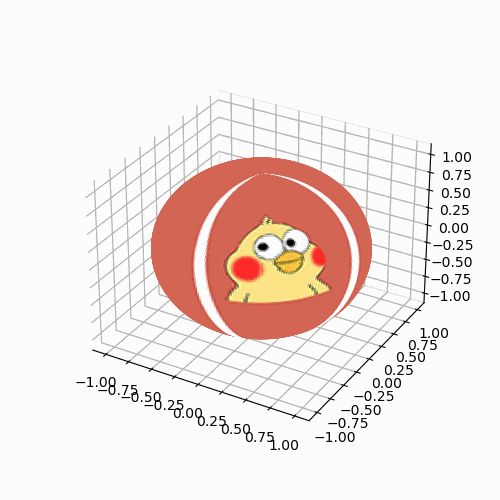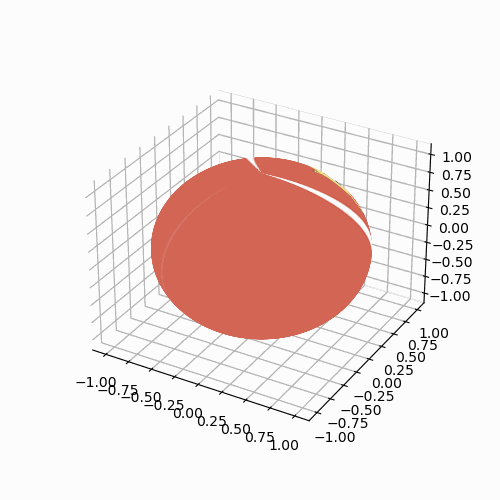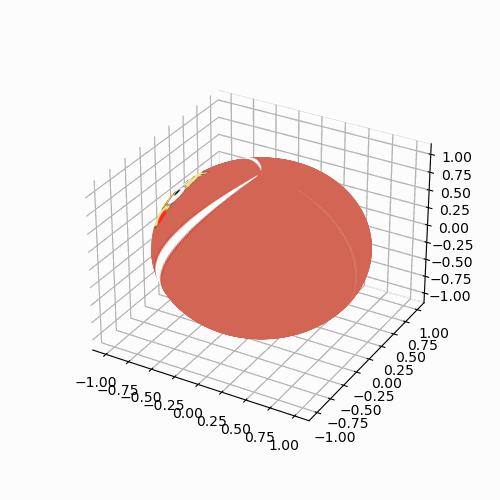
如何用Python把篮球和鸡联系起来
文章目录画个球让球转起来画个球 不管篮球和不和鸡联系起来,都首先得有个球,或者说要有一个球面,用参数方程可以表示为 xrcosϕcosθyrcosϕsinθzrsinϕ\begin{aligned} x & r\cos\phi\cos\theta\\ y & r\cos\phi\sin\th…...
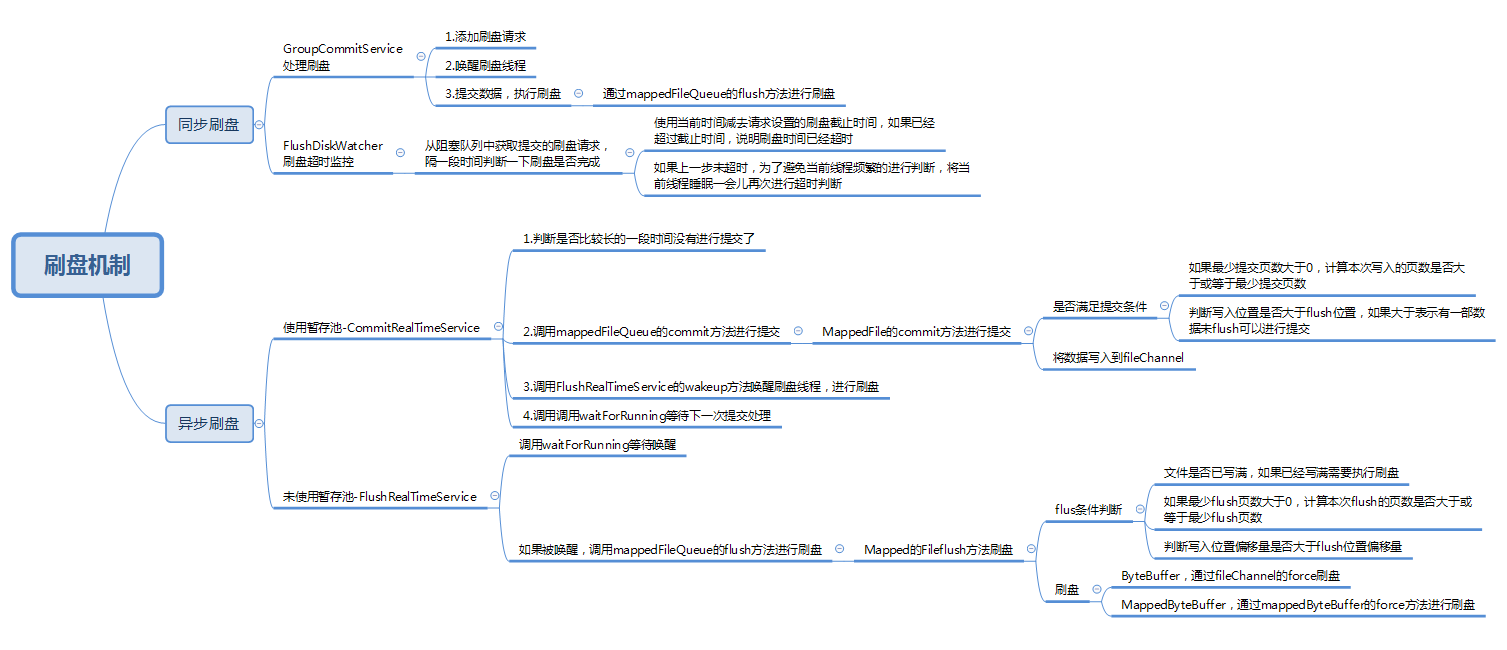
【RocketMQ】消息的刷盘机制
刷盘策略 CommitLog的asyncPutMessage方法中可以看到在写入消息之后,调用了submitFlushRequest方法执行刷盘策略: public class CommitLog {public CompletableFuture<PutMessageResult> asyncPutMessage(final MessageExtBrokerInner msg) {// …...

AMBA-AXI(一)burst 传输-INCR/WRAP/Fixed
💡Note:本文是根据AXI协议IHI0022F_b_amba_axi_protocol_spec.pdf(issue F)整理的。主要是分享AXI3.0和4.0部分。如果内容有问题请大家在评论区中指出,有补充或者疑问也可以发在评论区,互相学习ὤ…...
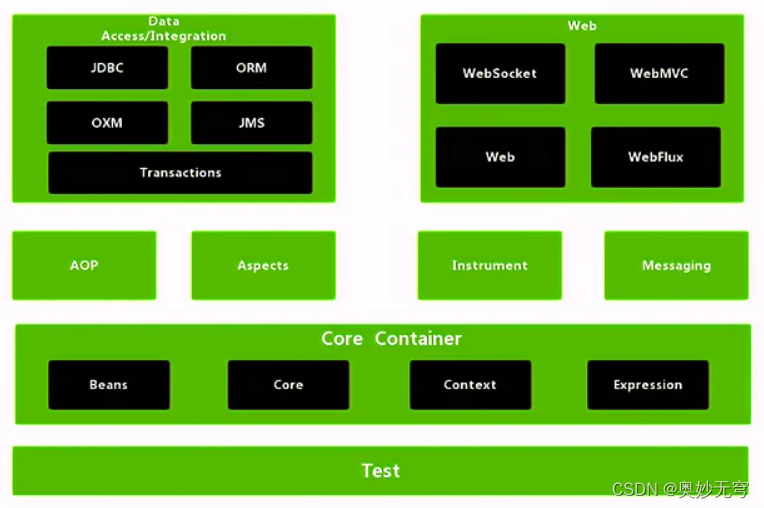
Java知识复习(八)Spring基础
1、什么是Spring框架? Spring :是一款开源的轻量级 Java 开发框架,旨在提高开发人员的开发效率以及系统的可维护性 2、Spring、SpringMVC和SpringBoot的区别 Spring主要指Spring Framework,就是指如上图所示的各项功能模块Spr…...

WuThreat身份安全云-TVD每日漏洞情报-2023-02-27
漏洞名称:OTFCC 缓冲区错误漏洞 漏洞级别:中危 漏洞编号:CVE-2022-35060,CNVD-2023-11996,CNNVD-202209-1527 相关涉及:OTFCC OTFCC 漏洞状态:EXP 参考链接:https://tvd.wuthreat.com/#/listDetail?TVD_IDTVD-2022-23648 漏洞名称:MuYucms 存在任意代码执行漏洞 漏洞级别:高危…...

上海交大陈海波教授、夏虞斌教授领衔巨作上市:《操作系统:原理与实现》
❤️作者主页:小虚竹 ❤️作者简介:大家好,我是小虚竹。2022年度博客之星评选TOP 10🏆,Java领域优质创作者🏆,CSDN博客专家🏆,华为云享专家🏆,掘金年度人气作…...

dpi数据接入shell脚
原文:dpi数据接入shell脚本_weixin_34416754的博客-CSDN博客 ##############从ftp服务器拿数据文件 #!/bin/bash #获取感知优良率DPI数据 #DCN服务器信息 uSichuan pS988188# ip137.192.5.53 #获取日期,根据日期抓取文件 Tdate -d "3 days ago&…...
Easyrecovery数据恢复软件工作原理及使用介绍教程
Easyrecovery是一款强大的数据恢复软件,它专门解决磁盘数据恢复问题。在计算机世界里,数据丢失经常是一件令人头疼的事情,但是有了Easyrecovery,您可以放心大胆地享受数据备份和恢复的乐趣。EasyRecovery使用Ontrack公司复杂的模式…...

【面试题】社招中级前端笔试面试题总结
大厂面试题分享 面试题库后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库typeof null 的结果是什么,为什么?typeof null 的结果是Object。在 JavaScript 第一个版本中,所有值都存储在…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
