代码随想录刷题题Day15
刷题的第十五天,希望自己能够不断坚持下去,迎来蜕变。😀😀😀
刷题语言:C++
Day15 任务
● 513.找树左下角的值
● 112. 路径总和 113.路径总和ii
● 106.从中序与后序遍历序列构造二叉树 105.从前序与中序遍历序列构造二叉树
1 找树左下角的值
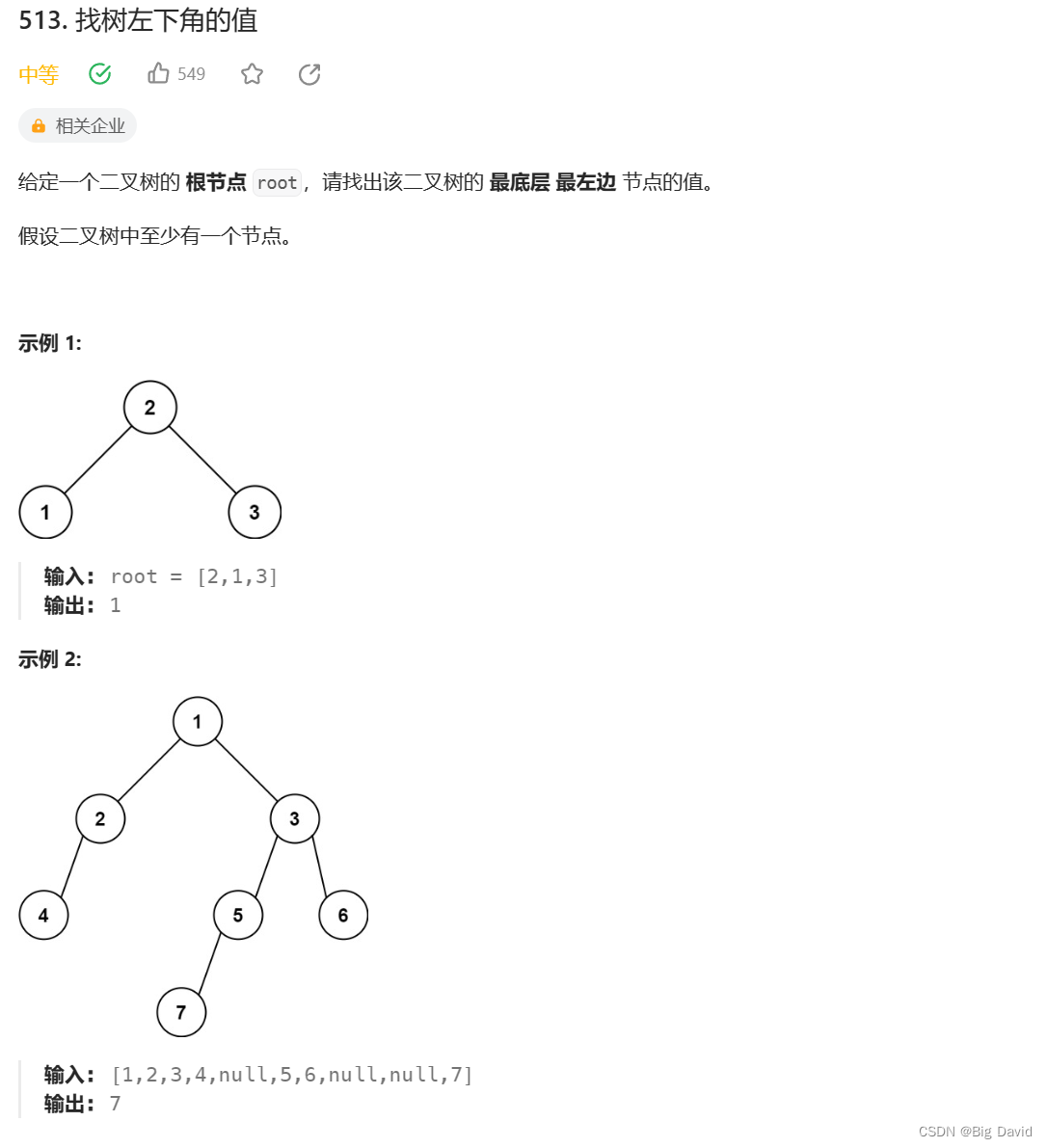
本题要找出树的最后一行最左边的值
思路1:层序遍历
思路2:递归
迭代法
层序遍历模板参考代码随想录刷题题Day12
class Solution {
public:int findBottomLeftValue(TreeNode* root) {queue<TreeNode*> que;int result;if (root != NULL) que.push(root);while (!que.empty()){int size = que.size();for (int i = 0; i < size; i++){TreeNode* node = que.front();que.pop();if (i == 0) result = node->val;// 记录最后一行第一个元素if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}return result;}
};
递归法
误区:不是一直向左遍历,最后一个就是答案
一直向左遍历到最后一个,未必是最后一行
关键:在树的最后一行找到最左边的值
(1) 判断最后一行:深度最大的叶子节点
(2) 最左边的值:可以使用前序遍历(当然中序,后序都可以,因为本题没有 中间节点的处理逻辑,只要左优先就行),保证优先左边搜索,然后记录深度最大的叶子节点,此时就是树的最后一行最左边的值。
(1)确定递归函数的参数和返回值
参数:要遍历的树的根节点,最长深度
返回值:void
int maxDepth = INT_MIN;// 全局变量 记录最大深度
int result; // 全局变量 最大深度最左节点的数值
void traversal(TreeNode* node, int depth)
(2)确定终止条件
当遇到叶子节点的时候,就需要统计一下最大的深度了,所以需要遇到叶子节点来更新最大深度。
if (node->left == NULL && node->right == NULL)
{if (depth > maxDepth){maxDepth = depth; // 更新最大深度result = node->val; // 最大深度最左面的数值}return;
}
(3)确定单层递归的逻辑
找最大深度的时候,递归的过程中依然要使用回溯
// 中
if (node->left) {// 左depth++;// 深度加一traversal(node->left, depth);depth--;// 回溯,深度减一
}
if (node->right) {// 右depth++;// 深度加一traversal(node->right, depth);depth--;// 回溯,深度减一
}
C++:
class Solution {
public:int maxDepth = INT_MIN;int result;void traversal(TreeNode* node, int depth) {if (node->left == NULL && node->right == NULL) {if (maxDepth < depth) {maxDepth = depth;result = node->val;}}if (node->left) {depth++;traversal(node->left, depth);depth--;}if (node->right) {depth++;traversal(node->right, depth);depth--;}return;}int findBottomLeftValue(TreeNode* root) {traversal(root, 0);return result;}
};
精简版本C++:
class Solution {
public:int maxDepth = INT_MIN;int result;void traversal(TreeNode* node, int depth) {if (node->left == NULL && node->right == NULL) {if (maxDepth < depth) {maxDepth = depth;result = node->val;}}if (node->left) {traversal(node->left, depth + 1);// 隐藏着回溯}if (node->right) {traversal(node->right, depth + 1);// 隐藏着回溯}return;}int findBottomLeftValue(TreeNode* root) {traversal(root, 0);return result;}
};
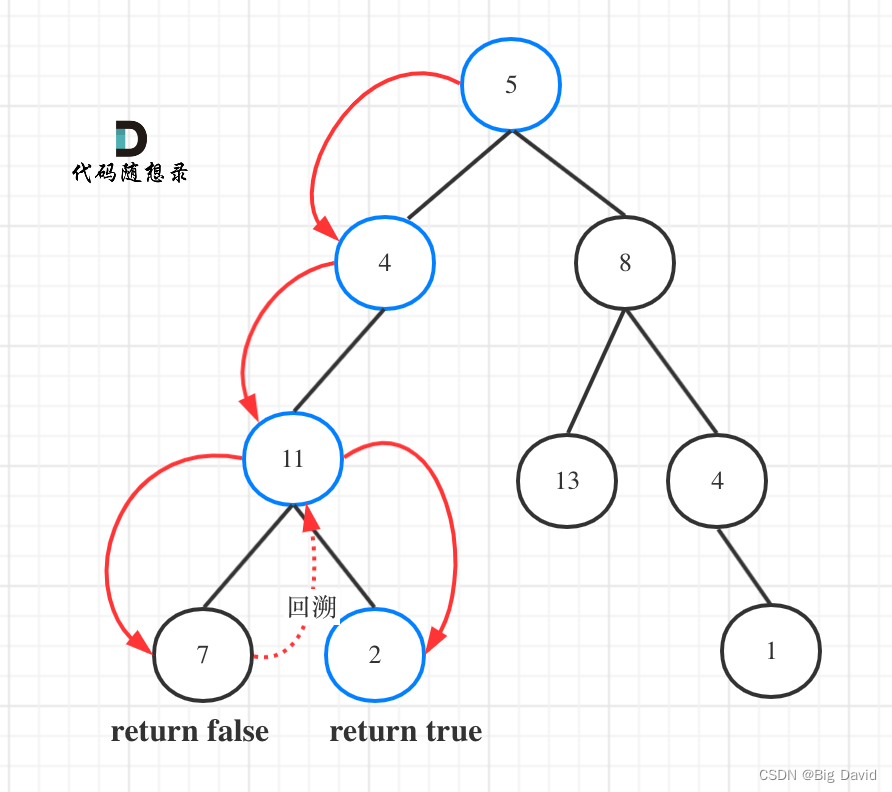
2 路径总和
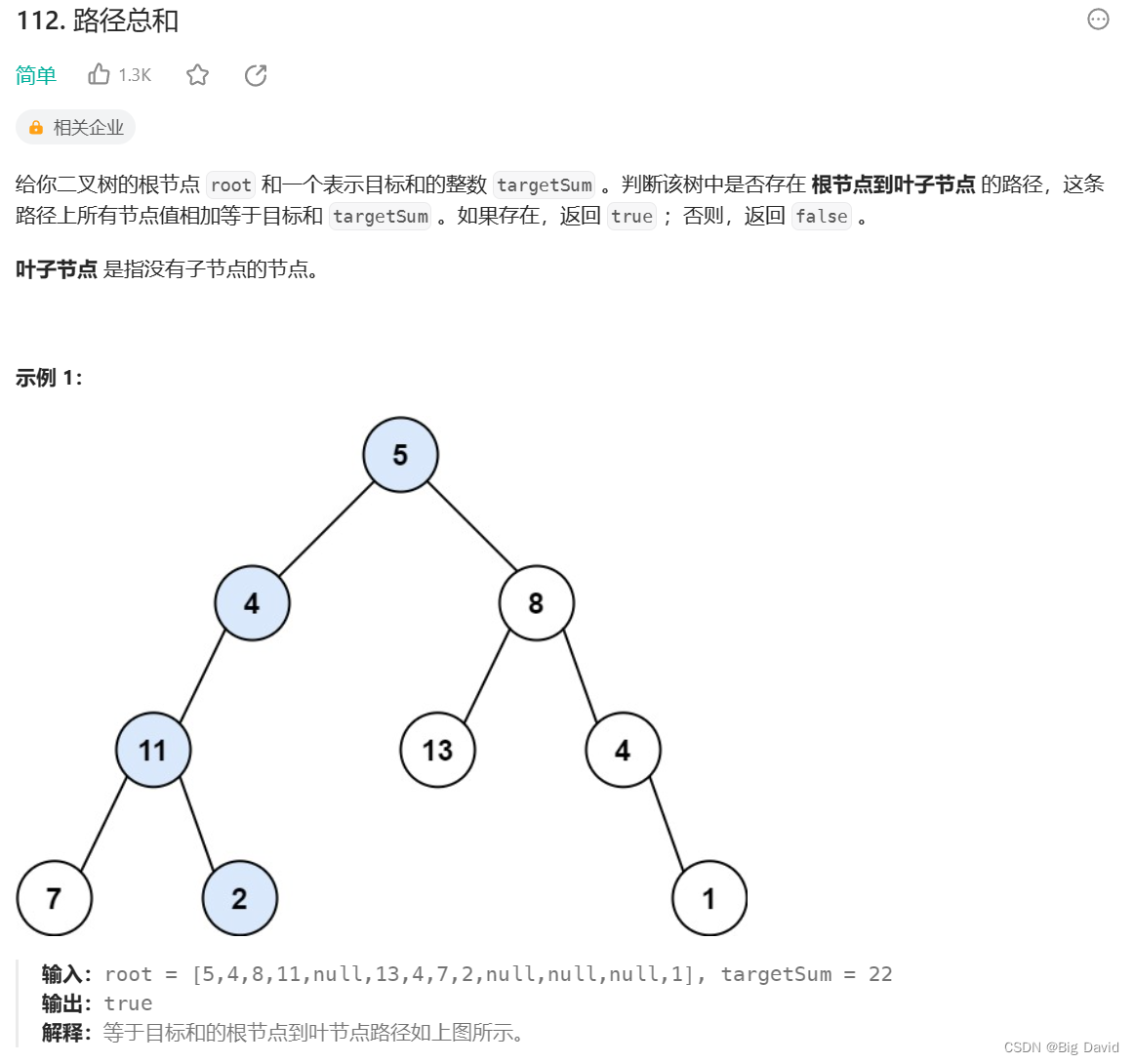
思路:
使用深度优先遍历的方式,本题前中后序都可以,因为中间节点没有处理逻辑
递归法
(1)确定递归函数的参数和返回类型
参数:二叉树的根节点、计算器(用来计算二叉树的一条边之和是否正好是目标和)
返回值:要找一条符合条件的路径,所以递归函数需要返回值,遍历的路线,并不要遍历整棵树,及时返回,返回类型是bool
递归函数返回值:
(1)如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值
(2)如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。
(3)如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回
bool traversal(TreeNode* node, int count)
(2)确定终止条件
计数器count初始为目标和,然后每次减去遍历路径节点上的数值
- 如果最后count == 0,同时到了叶子节点的话,说明找到了目标和
- 如果遍历到了叶子节点,count不为0,就是没找到
if (node->left == NULL && node->right == NULL && count == 0) return true;
if (node->left == NULL && node->right == NULL && count != 0) return false;
(3)确定单层递归的逻辑
递归函数是有返回值的,如果递归函数返回true,说明找到了合适的路径,应该立刻返回
if (node->left) {// 左 (空节点不遍历)// 遇到叶子节点返回true,则直接返回trueif (traversal(node->left, count - node->left->val)) return true;
}
if (node->right) {// 右 (空节点不遍历)// 遇到叶子节点返回true,则直接返回trueif (traversal(node->right, count - node->right->val)) return true;
return false;
把回溯的过程表现出来:
if (node->left) {// 左count -= node->left->val;// 递归,处理节点;if (traversal(node->left, count)) return true;count += node->left->val;// 回溯,撤销处理结果
}
if (node->right) { // 右count -= node->right->val;if (traversal(node->right, count)) return true;count += node->right->val;// 回溯,撤销处理结果
}
C++:
class Solution {
public:bool traversal(TreeNode* node, int count) {if (node->left == NULL && node->right == NULL && count == 0) return true;// 遇到叶子节点,并且计数为0if (node->left == NULL && node->right == NULL && count != 0) return false;// 遇到叶子节点直接返回if (node->left) {// 左count -= node->left->val;// 递归,处理节点;if (traversal(node->left, count)) return true;count += node->left->val;// 回溯,撤销处理结果}if (node->right) {// 右count -= node->right->val;// 递归,处理节点if (traversal(node->right, count)) return true;count += node->right->val;// 回溯,撤销处理结果}return false;}bool hasPathSum(TreeNode* root, int targetSum) {if (root == NULL) return false;return traversal(root, targetSum - root->val);}
};
精简版本C++:
class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if (!root) return false;if (!root->left && !root->right && targetSum == root->val) {return true;}return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);}
};
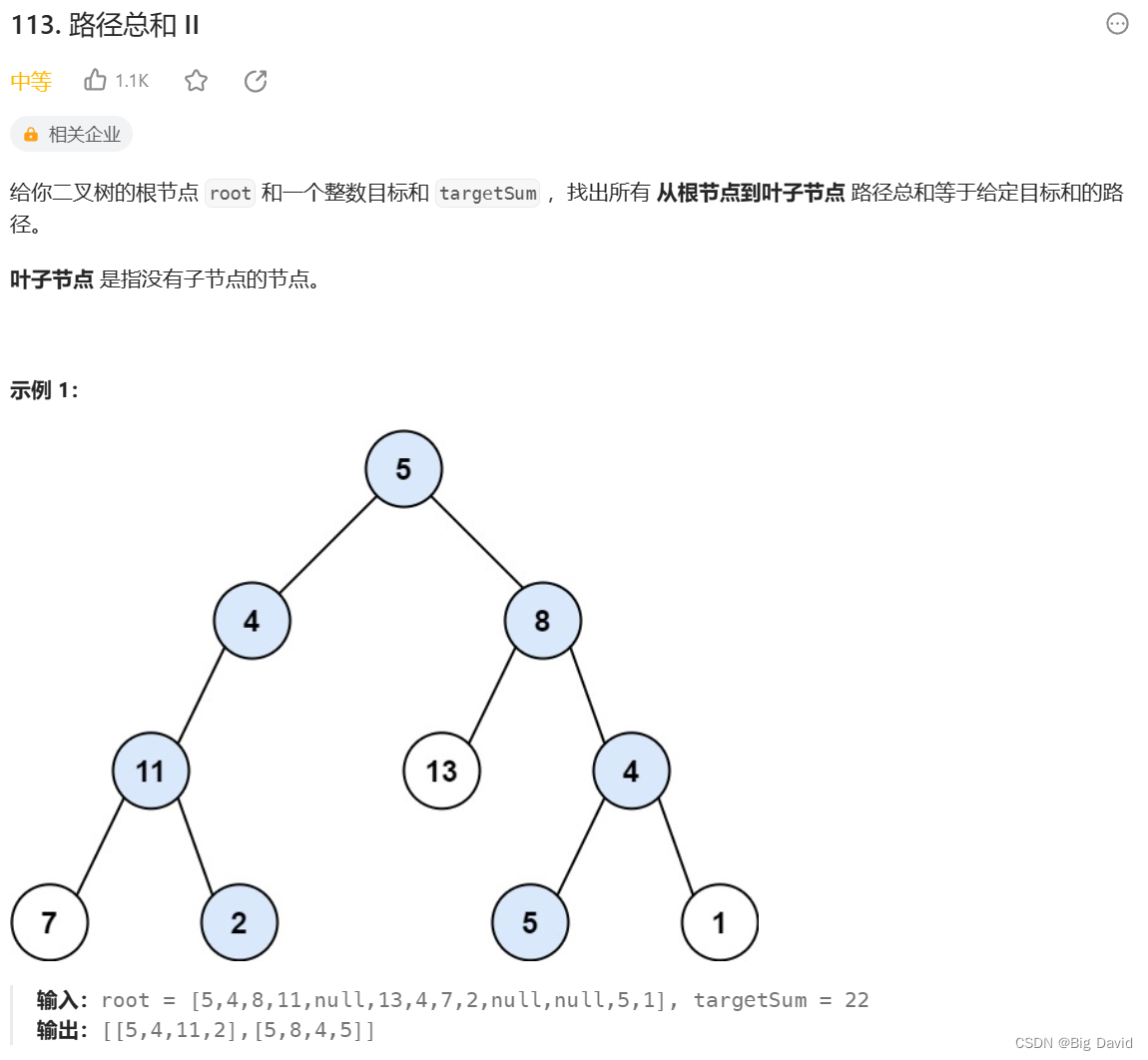
思路:
路径总和ii要遍历整个树,找到所有路径,所以递归函数不要返回值!
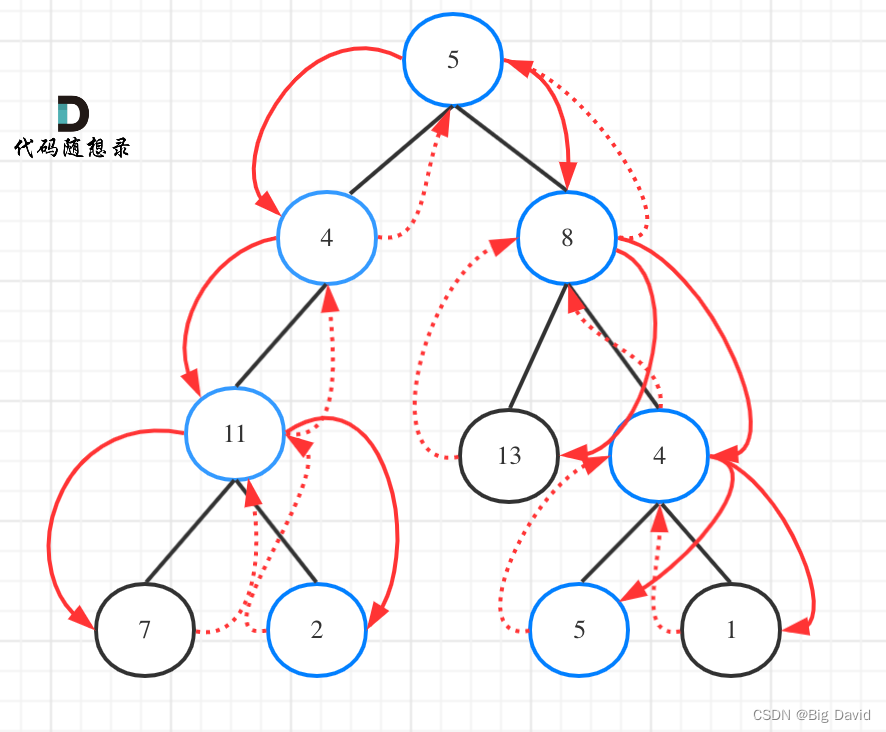
class Solution {
public:vector<vector<int>> result;vector<int> path;// 递归函数不需要返回值,因为我们要遍历整个树void traversal(TreeNode* node, int count) {if (node->left == NULL && node->right == NULL && count == 0) {result.push_back(path);return;}if (node->left == NULL && node->right == NULL) return;// 遇到叶子节点而没有找到合适的边,直接返回if (node->left) {// 左 (空节点不遍历)path.push_back(node->left->val);count -= node->left->val;traversal(node->left, count);// 递归count += node->left->val;// 回溯path.pop_back();// 回溯}if (node->right) {// 右 (空节点不遍历)path.push_back(node->right->val);count -= node->right->val;traversal(node->right, count);// 递归count += node->right->val;// 回溯path.pop_back();// 回溯}return;}vector<vector<int>> pathSum(TreeNode* root, int targetSum) {result.clear();path.clear();if (root == NULL) return result;path.push_back(root->val);// 把根节点放进路径traversal(root, targetSum - root->val);return result;}
};
3 从中序与后序遍历序列构造二叉树
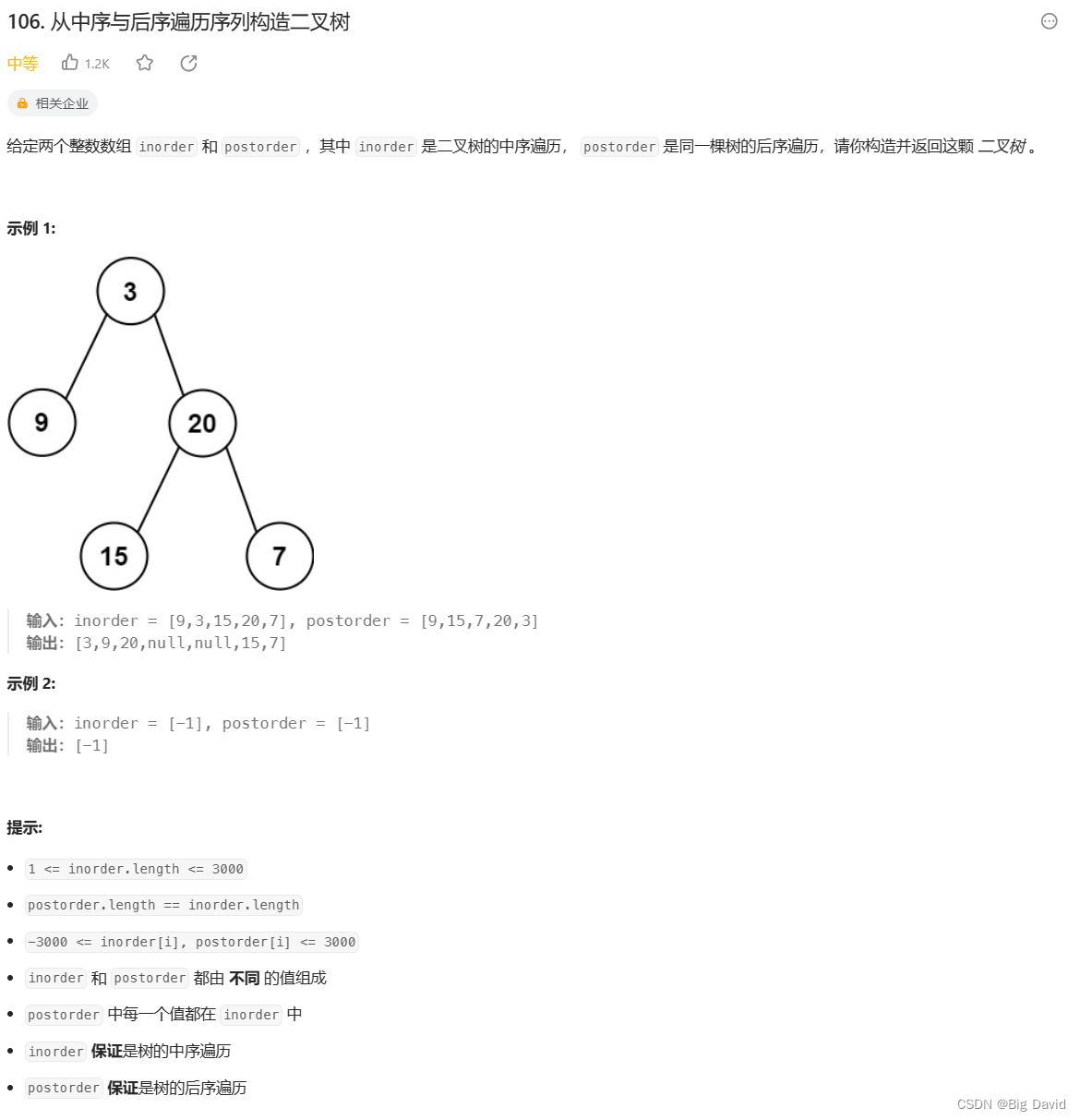
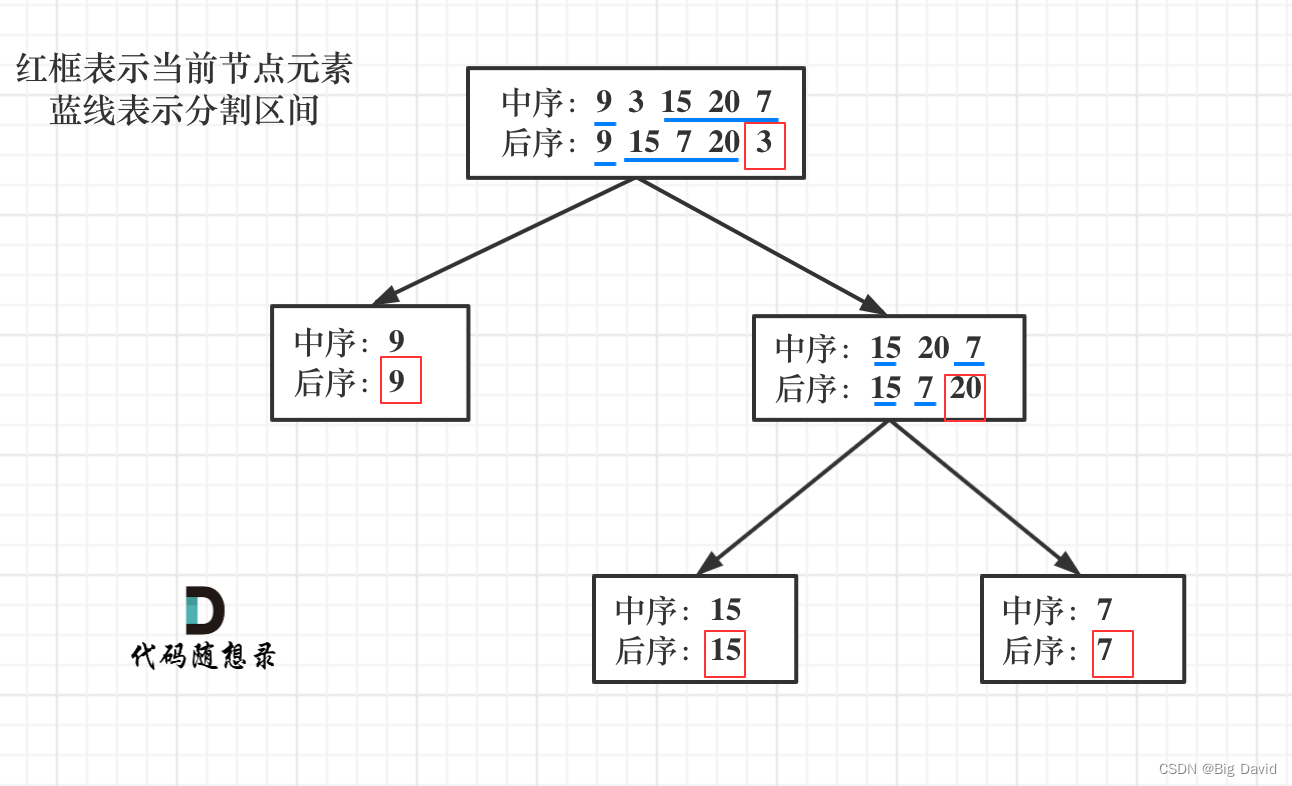
思路:
- 后序数组为0,空节点
- 后序数组最后一个元素为节点元素
- 寻找中序数组位置作为切割点
- 切中序数组
- 切后序数组
- 递归处理左右区间
C++:
class Solution {
public:TreeNode* traversal(vector<int>& inorder, vector<int>& postorder) {if (postorder.size() == 0) return NULL;// 后序遍历数组最后一个元素,就是当前的中间节点int rootValue = postorder[postorder.size() - 1];TreeNode* root = new TreeNode(rootValue);// 叶子节点if (postorder.size() == 1) return root;// 找到中序遍历的切割点int index;for (index = 0; index < inorder.size(); index++){if (inorder[index] == rootValue) break;}// 切割中序数组vector<int> leftInorder(inorder.begin(), inorder.begin() + index);vector<int> rightInorder(inorder.begin() + index + 1, inorder.end());postorder.resize(postorder.size() - 1);// 切割后序数组vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());root->left = traversal(leftInorder, leftPostorder);root->right = traversal(rightInorder, rightPostorder);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if (inorder.size() == 0 || postorder.size() == 0) return NULL;return traversal(inorder, postorder);}
};
4 从前序与中序遍历序列构造二叉树
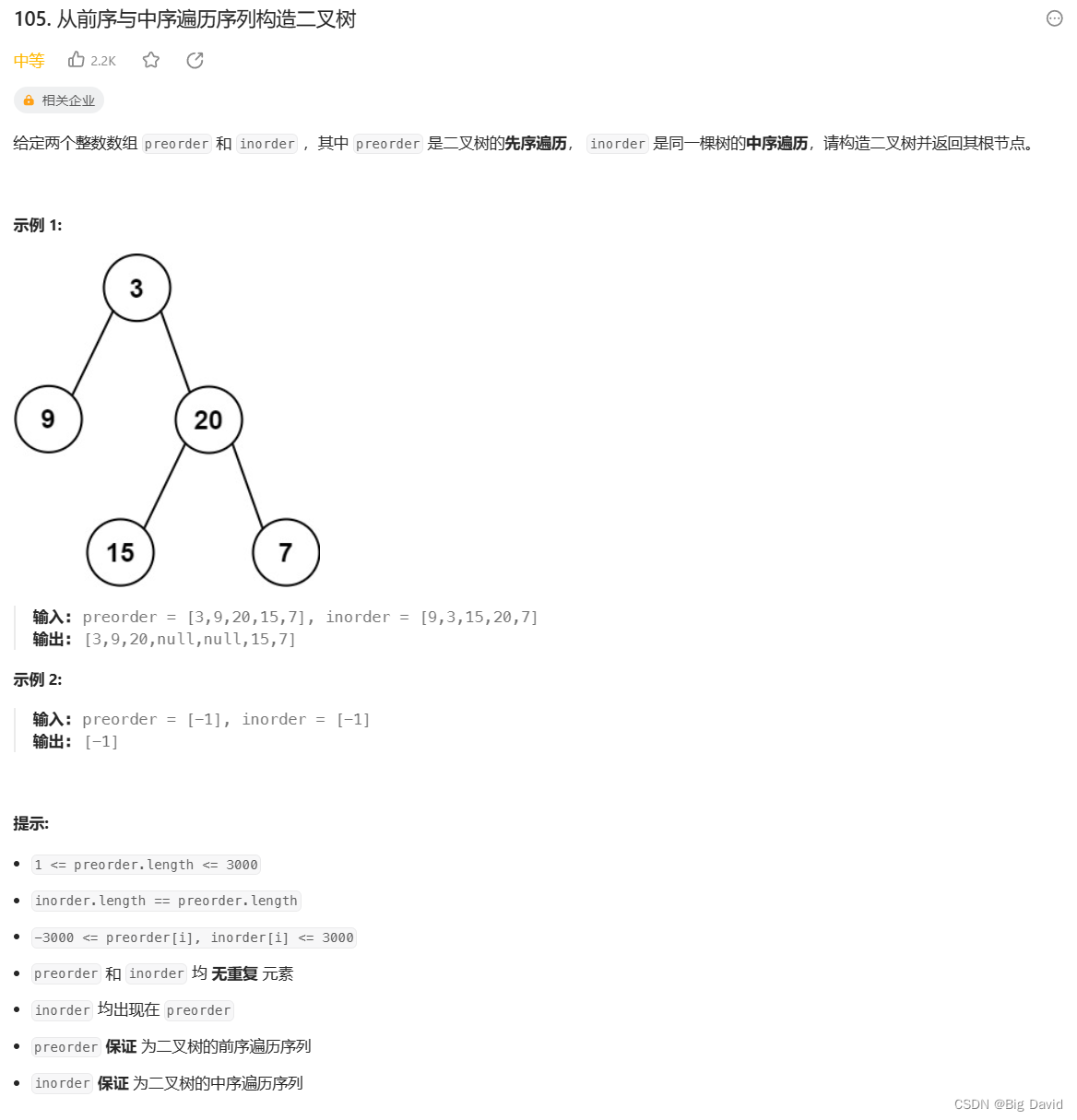
思路:
- 前序数组为0,空节点
- 前序数组第一个元素为节点元素
- 寻找中序数组位置作为切割点
- 切中序数组
- 切前序数组
- 递归处理左右区间
C++:
class Solution {
public:TreeNode* traversal(vector<int>& preorder, vector<int>& inorder) {// 前序数组为0,空节点if (preorder.size() == 0) return NULL;// 前序数组第一个元素为节点元素int rootValue = preorder[0];TreeNode* root = new TreeNode(rootValue);if (preorder.size() == 1) return root;// 寻找中序数组位置作为切割点int index;for (index = 0; index < inorder.size(); index++) {if (inorder[index] == rootValue) break;}// 切中序数组vector<int> leftInorder(inorder.begin(), inorder.begin() + index);vector<int> rightInorder(inorder.begin() + index + 1, inorder.end());// 切前序数组preorder.erase(preorder.begin());vector<int> leftPreorder(preorder.begin(), preorder.begin() + leftInorder.size());vector<int> rightPreorder(preorder.begin() + leftPreorder.size(), preorder.end());// 递归处理左右区间root->left = traversal(leftPreorder, leftInorder);root->right = traversal(rightPreorder, rightInorder);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if (preorder.size() == 0 || inorder.size() == 0) return NULL;return traversal(preorder, inorder);}
};
鼓励坚持十六天的自己😀😀😀
相关文章:

代码随想录刷题题Day15
刷题的第十五天,希望自己能够不断坚持下去,迎来蜕变。😀😀😀 刷题语言:C Day15 任务 ● 513.找树左下角的值 ● 112. 路径总和 113.路径总和ii ● 106.从中序与后序遍历序列构造二叉树 105.从前序与中序遍历…...
软件设计师——信息安全(一)
📑前言 本文主要是【信息安全】——软件设计师——信息安全的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是听风与他🥇 ☁️博客首页:CSDN主页听风与他 🌄…...

git必须掌握:git远程变动怎么解决
如何已经指定了选择分支 那下面的分支名称可以省略 如果远程分支存在变动,通常 git 推送的流程如下: 首先,使用 git fetch 命令从远程仓库获取最新的分支信息和变动。 git fetch然后,可以使用 git merge 或者 git rebase 命令进…...

Python里的时间模块
time 模块 时间表示方式 时间戳 timestamp:表示的是从 1970 年1月1日 00:00:00 开始按秒计算的偏移量UTC(Coordinated Universal Time, 世界协调时)亦即格林威治天文时间,世界标准时间。在中国为 UTC+8 DST(Daylight Saving Time) 即夏令时;结构化时间(struct_time): …...
SCI一区级 | Matlab实现GWO-CNN-GRU-selfAttention多变量多步时间序列预测
SCI一区级 | Matlab实现GWO-CNN-GRU-selfAttention多变量多步时间序列预测 目录 SCI一区级 | Matlab实现GWO-CNN-GRU-selfAttention多变量多步时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.Matlab实现GWO-CNN-GRU-selfAttention灰狼算法优化卷积门控循环…...

C#学习相关系列之自定义遍历器
在C#中,自定义遍历器需要实现IEnumerable接口和IEnumerator接口。其中,IEnumerable接口包含一个GetEnumerator方法,该方法返回一个IEnumerator接口的实例,而IEnumerator接口包含Current、MoveNext和Reset方法。 IEnumerable&#…...
WPS没保存关闭了怎么恢复数据?3个方法,完成数据恢复!
“我今天在使用WPS时,突然有点急事出去了一趟,但是我忘记保存文档了,回来之后发现电脑自动关机了,我的文档也没了!这可怎么办呢?有什么办法可以找回这些数据吗?” 在快节奏的工作中,…...
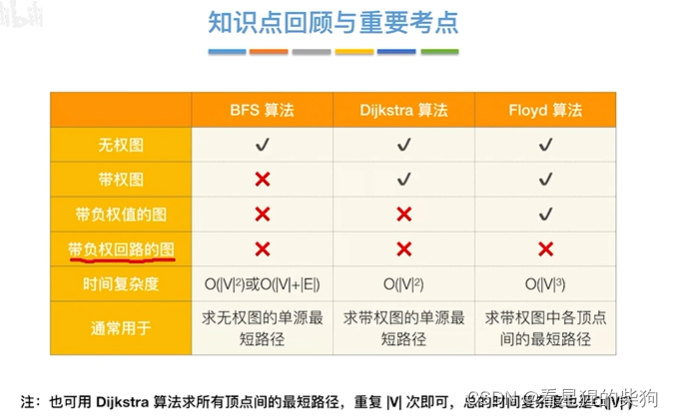
数据结构和算法-最小生成树(prim和krusakal)和最短路径问题(BFS和dijkastra和floyd)
文章目录 最小生成树总览生成树广度优先生成树深度优先生成树最小生成树Prim算法Kruskal算法Prim vs KrusakalPrim的实现Kruskal的实现 小结 最短路径问题单源最短路径问题BFS求无权图的单源最短路径小结Dijkastra算法算法时间复杂度不适用情况 每一对顶点的最短路径问题Floyd算…...
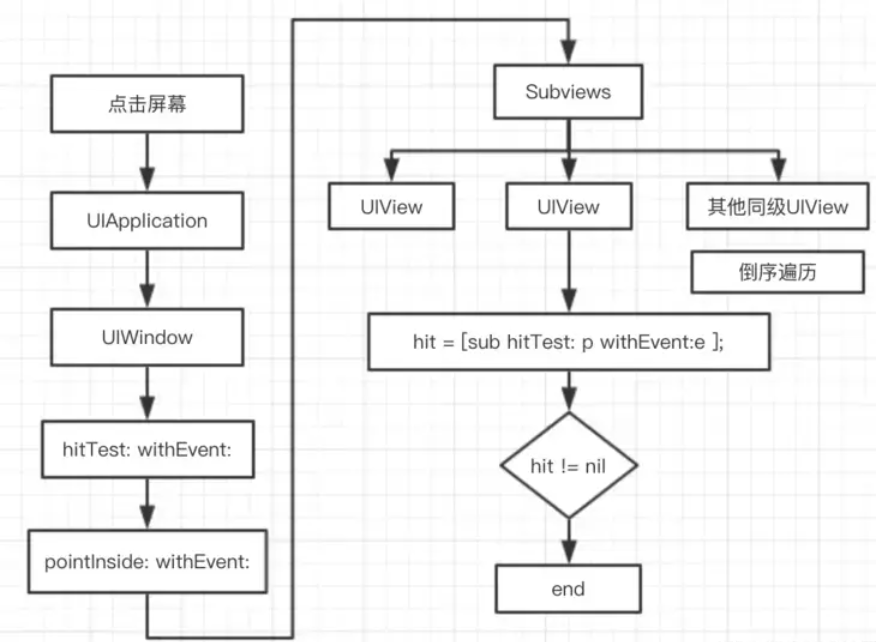
响应者链概述
响应者链 iOS事件的3大类型 Touch Events(触摸事件)Motion Events(运动事件,比如重力感应和摇一摇等)Remote Events(远程事件,比如用耳机上得按键来控制手机) 触摸事件 处理触摸事件的两个步骤 寻找事件的最佳响应者事件的响应在响应链中的传递 寻…...
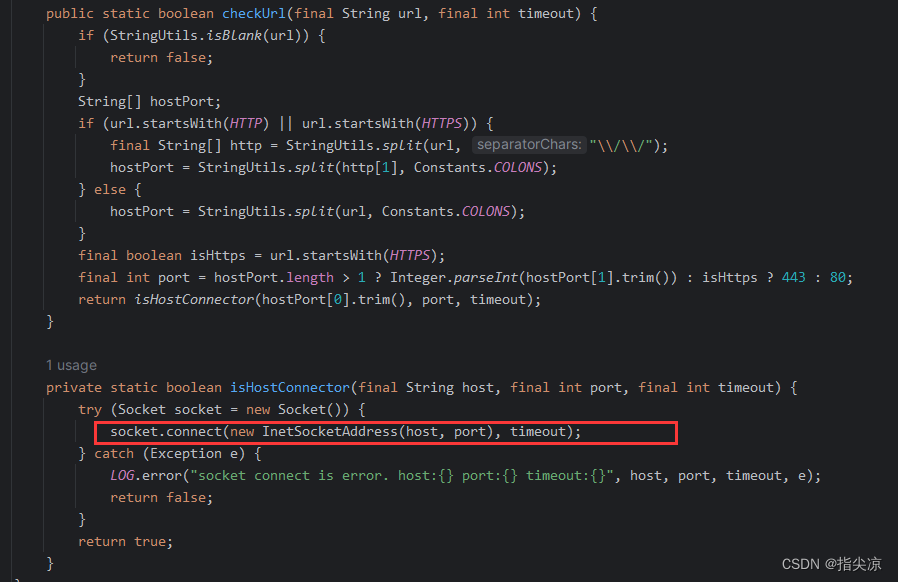
ShenYu网关Http服务探活解析
文章目录 网关端服务探活admin端服务探活 Shenyu HTTP服务探活是一种用于检测HTTP服务是否正常运行的机制。它通过建立Socket连接来判断服务是否可用。当服务不可用时,将服务从可用列表中移除。 网关端服务探活 以divide插件为例,看下divide插件是如何获…...
基于dockerfile搭建LNMP
组件自定义IP所需组件nginx172.111.0.10nginxwordpressmysql172.111.0.20mysql-5.7.20php172.111.0.30php LNMP介绍 L:Linux平台,操作系统,另外桑组件的运行平台 N:nginx 提供前端页面 M:MySQL,开源关系的…...
基于VGG-16+Android+Python的智能车辆驾驶行为分析—深度学习算法应用(含全部工程源码)+数据集+模型(三)
目录 前言总体设计系统整体结构图系统流程图 运行环境模块实现1. 数据预处理2. 模型构建3. 模型训练及保存1)模型训练2)模型保存 4. 模型生成1)模型导入及调用2)相关代码(1)布局文件(2ÿ…...
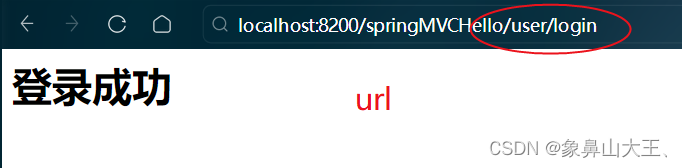
springMVC-@RequestMapping
基本介绍 RequestMapping注解可以指定控制器/处理器的某个方法的请求的url, 示例 (结合springMVC基本原理理解) Controller public class UserHandler {RequestMapping(value "/login")public String login() {System.out.println("登…...

智能优化算法应用:基于树种算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于树种算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于树种算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.树种算法4.实验参数设定5.算法结果6.参考文献7.MA…...

web前端项目-影视网站开发
影视网站 本项目主要使用到了 HTML;CSS;JavaScript脚本技术;AJAX无刷新技术;jQuery等技术实现了动态影视网页 运行效果: 一:index.html <!DOCTYPE> <html lang"en"> <head>…...
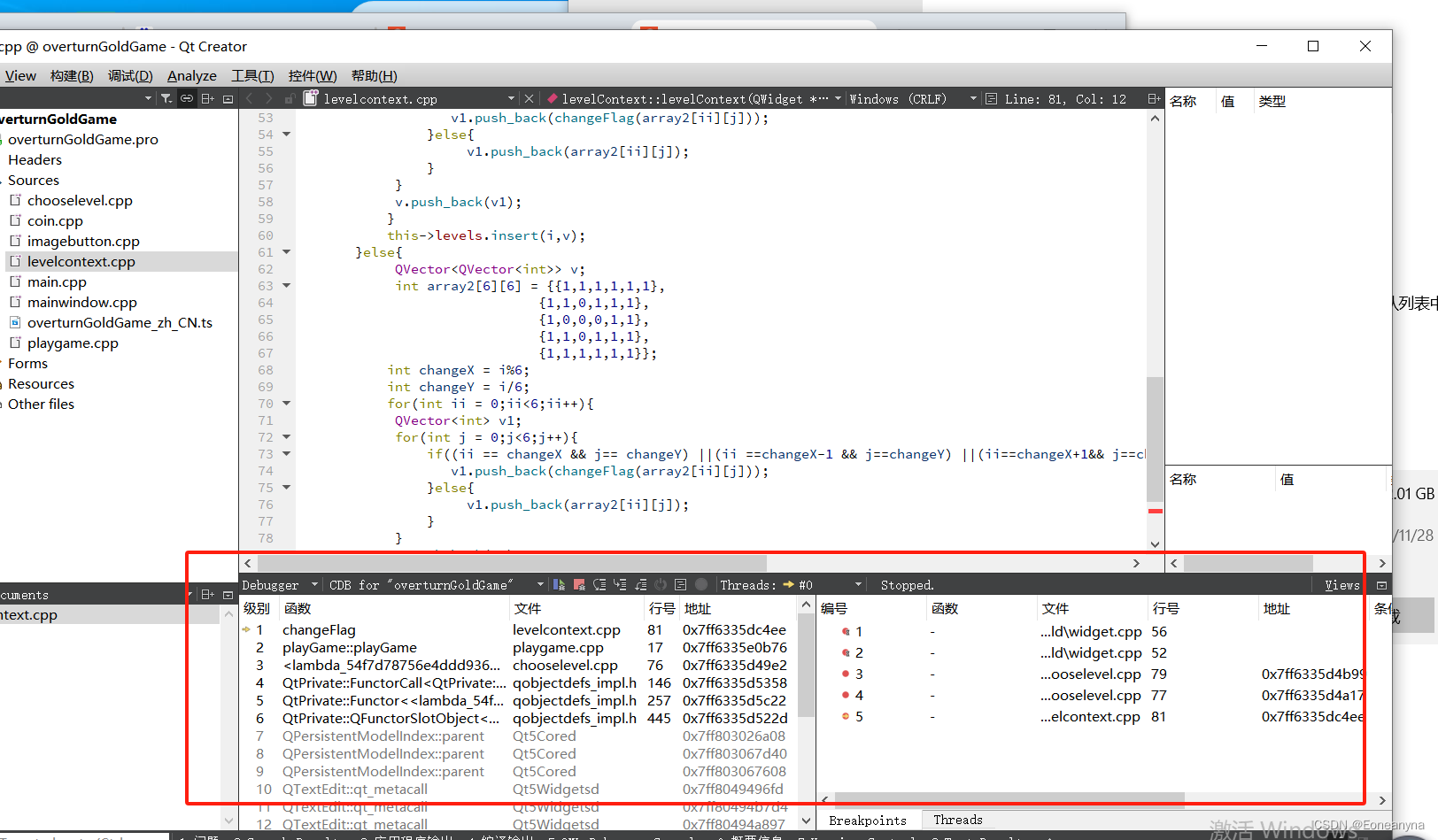
QT:Unable to create a debugging engine.
debug跑不了: 报错:Unable to create a debugging engine. 参考: https://blog.csdn.net/u010906468/article/details/104716198 先检查是否安装了DEBUG插件 工具-》》选项 查看插件,如果没有的话,需要重新安装qt时…...

如何理解Rust语言中的“impl”关键字
在Rust编程语言中,impl是一个关键字,用于为类型实现方法和特性(traits)。impl关键字后面可以跟一个类型或者特性名称,然后在大括号中定义该类型或特性的具体实现。 当我们使用impl关键字为一个类型实现方法时…...

C++实现简单的猜数字小游戏
猜数字 小游戏介绍:猜数字游戏是令游戏机随机产生一个100以内的正整数,用户输入一个数对其进行猜测,需要你编写程序自动对其与随机产生的被猜数进行比较,并提示大了,还是小了,相等表示猜到了。如果猜到&…...

人工智能导论复习资料
题型 1、简答题(5题) 2、设计题 3、综合题 4、论述题(10分) 考点 第一章 1、人工智能的定义、发展; 2、人工智能的学派、认知观及其间的关系; 3、人工智能要素及系统分类; 4、人工智能的研究、…...

Sentinel使用详解
组件简介 Sentinel是阿里开源的一套用于服务容错的综合性解决方案。它以流量为切入点,从流量控制、熔断降级、系统负载保护等多个维度来保护服务的稳定性。Sentinel承接了阿里巴巴近10年的双十一大促流量的核心场景,例如秒杀、消息削峰填谷、集群流量控…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...