保姆级 Keras 实现 YOLO v3 三
保姆级 Keras 实现 YOLO v3 三
- 一. 分配 anchor box
- 二. 正负样本匹配规则
- 三. 为每一个 anchor box 打标签
- 3.1 anchor box 长什么样?
- 3.2 每一个 anchor box 标签需要填充的信息有哪些?
- 3.3 ( Δ x , Δ y , Δ w , Δ h ) (\Delta x, \Delta y, \Delta w, \Delta h) (Δx,Δy,Δw,Δh) 怎么填?
- 3.4 类别标签怎么填?
- 3.5 置信度标签怎么填?
- 四. 打标签代码
- 五. 代码下载
上一篇 文章中, 我们完成了读标注文件和聚类生成 k k k 个 anchor box, 接下来就是要为特征图的每一个 grid cell ( c h a n n e l s = 75 ) (channels = 75) (channels=75) 打标签了
上面讲为 每一个 grid cell ( c h a n n e l s = 75 ) (channels = 75) (channels=75) 打标签 而不为 每一个 anchor box 打标签 , 其实两句话是同一个意思, 但是最终反应到损失函数计算的时候, 其实是计算每个 grid cell 的 n n n 个通道对应于标签值的损失. 损失函数并不知道什么是 anchor box, 它只管数学上的计算式, 那要计算就需要网络的输出格式与标签格式在数学表达式上的匹配. 将 anchor box 对应的标签信息拉直打平放到 grid cell 的 n n n 个通道中, 那就是网络输出对应的真值了
在 《保姆级 Keras 实现 YOLO v3 一》 中我们知道网络输出有三个特征图, 三个特征图大小成倍递减, 是为了适应不同尺度的目标. 那一个 ground truth 对应这三个特征图的哪一个呢? 又对应某一特征图中的哪一个 grid cell 呢? 一个 grid cell 中有 k k k 个 anchor box, 又对应其中的哪一个呢?
一. 分配 anchor box
在 上一篇 文章中, 我们从小到大排列了 9 9 9 个聚类出来的 anchor box 尺寸, 有三个特征图, 正好一个特征图可以平均分配三个, 所以前三个就分配给预测小目标的 52 × 52 52 \times 52 52×52 的特征图, 中间三个就分配给预测中等大小目标的 26 × 26 26 \times 26 26×26 的特征图, 剩下的三个分配给预测大目标的 13 × 13 13 \times 13 13×13 的特征图. 这样, 每个特征图的每个 grid cell 就分配到了三个 anchor box
二. 正负样本匹配规则
训练的时候输出是未知的, 我们需要 ground truth 来调整网络的参数, 让输出向 ground truth 靠近. 就需要为每一个输出确定一个靠近的真值用于损失计算
由 YOLO v3 网络结构我们知道在一张图像中有 13 × 13 × 3 + 26 × 26 × 3 + 52 × 52 × 3 = 10 , 647 13 × 13 × 3 + 26 × 26 × 3 + 52 × 52 × 3 = 10,647 13×13×3+26×26×3+52×52×3=10,647 个 anchor box, 正负样本的匹配规则如下
- 正样本: 一张图中对于第 j j j 个 ground truth, 找出包含它的中心点的那个 grid cell 的 k k k 个 anchor box, 分别计算 I o U IoU IoU, 选 I o U IoU IoU 最大的那一个 anchor box 当成正样本. 就算 I o U IoU IoU 低于阈值也当成正样本, 要不然就会出现某个 ground truth 没有对应的 anchor box. 一个 anchor box 只能分配给一个 ground truth
- 负样本: 除正样本外, 对第 i i i 个 anchor box, 遍历一张图中所有 ground truth, 记录最大的 I o U IoU IoU 值, 如果最大的 I o U IoU IoU 小于阈值, 那这个 anchor box 就是负样本
- 忽略样本: 除正负样本外, 都为忽略样本
按照上面的规则会有一个小问题, 就是正样本会很少, 因为 ground truth 的数量等于正样本的数量, 而一张图中的目标通常是很少的, 所以就会造成样本不均衡. 要解决这个问题就需要修改一下正样本的匹配规则, 修改后如下
- 正样本: 一张图中对于第 j j j 个 ground truth, 找出包含它的中心点的那个 grid cell 的 k k k 个 anchor box, 分别计算 I o U IoU IoU, 选 I o U IoU IoU 最大的那一个 anchor box 当成正样本. 就算 I o U IoU IoU 低于阈值也当成正样本. 对于剩下的 k − 1 k -1 k−1 个 anchor box, 如果它与第 j j j 个 ground truth 的 I o U IoU IoU 大于一个较大的阈值, 比如 0.7 0.7 0.7, 都将这些 anchor box 分配为 第 j j j 个 ground truth 的正样本. 一个 anchor box 只能分配给一个 ground truth
在有一些实现中, 计算正样本的 I o U IoU IoU 时, 将 ground truth 和 anchor box 的一个角移动到相同的位置, 比如下图, 将左上角移动到相同的位置. 计算方式就和聚类时计算 I o U IoU IoU 是一样的
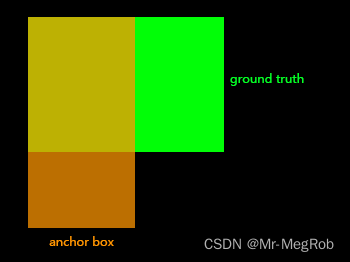
两个方式其实差异不大, 因为 ground truth 和 anchor box 的中心距离并不远, 所以交集面积是差不多的, 甚至大部分计算结果是一样的. 这也就导致了两种计算方式差异不大
三. 为每一个 anchor box 打标签
3.1 anchor box 长什么样?
网络输入是 416 × 416 416 \times 416 416×416, 52 × 52 52 \times 52 52×52 的特征图相比于原图缩小了 8 8 8 倍, 所以在原图中每隔 8 8 8 个像素放三个最小尺寸的 anchor box, 三个 anchor box 中心重叠. 如下图, 图中一个小格表示一个像素
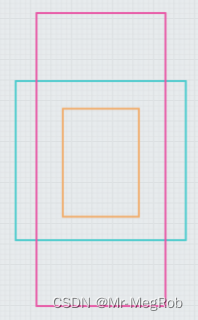
26 × 26 26 \times 26 26×26 的特征图缩小了 16 16 16 倍, 所以就是每隔 16 16 16 个像素放三个中等尺寸的 anchor box, 类推 13 × 13 13 \times 13 13×13 特征图每隔 32 32 32 个像素就放最大的三个 anchor box
3.2 每一个 anchor box 标签需要填充的信息有哪些?
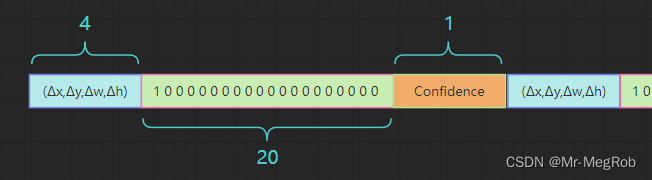
我们要预测 anchor box 的修正量 ( Δ x , Δ y , Δ w , Δ h ) (\Delta x, \Delta y, \Delta w, \Delta h) (Δx,Δy,Δw,Δh), 类别( 20 20 20 类), 还有要有一个置信度 C ∈ [ 0 , 1 ] C \in [0, 1] C∈[0,1], 所以一个 anchor box 需要的参数有 25 25 25 个, 一个 grid cell 有 3 3 3 个 anchor box, 所以一个 grid cell 需要 75 75 75 个参数, 这 75 75 75 个参数就填充一个 grid cell 的 75 75 75 个通道, 3 3 3 个 anchor box 的数据依次排列即可, 你要喜欢也可以按你想的顺序排列
3.3 ( Δ x , Δ y , Δ w , Δ h ) (\Delta x, \Delta y, \Delta w, \Delta h) (Δx,Δy,Δw,Δh) 怎么填?
我们要清楚一点, 网络对目标位置预测的是对于 anchor box 变换到 ground truth 的修正量 ( Δ x , Δ y , Δ w , Δ h ) (\Delta x, \Delta y, \Delta w, \Delta h) (Δx,Δy,Δw,Δh), 而不是直接预测目标的绝对坐标位置, 现在看图说话
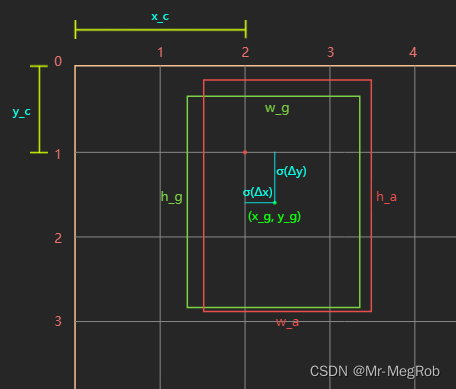
上图中, 绿色框表示 ground truth, 坐标表示形式是 ( x , y , w , h ) (x, y, w, h) (x,y,w,h), 其中 x , y x, y x,y 表示中心坐标, w , h w, h w,h 表示宽和高, 对应到图中便是 ( x g , y g , w g , h g ) (x_g, y_g, w_g, h_g) (xg,yg,wg,hg), 红色框表示一个 anchor box. 它的中心是 grid cell 的坐标 ( x c , y c ) (x_c, y_c) (xc,yc), 其宽和高分别是 w a , h a w_a, h_a wa,ha. 好了, 现在我们用网络的输出 ( t x , t y , t w , t h ) (t_x, t_y, t_w, t_h) (tx,ty,tw,th) 来修正 anchor box, 之所以用 ( t x , t y , t w , t h ) (t_x, t_y, t_w, t_h) (tx,ty,tw,th) 来表示预测值, 是因为我们要用 ( Δ x , Δ y , Δ w , Δ h ) (\Delta x, \Delta y, \Delta w, \Delta h) (Δx,Δy,Δw,Δh) 来表示标签值. 不要弄混了. 公式如下
x g = σ ( t x ) + x c y g = σ ( t y ) + y c w g = w a e t w h g = h a e t h \begin{aligned} x_g&= \sigma(t_x) + x_c \\ y_g &= \sigma(t_y) + y_c \\ w_g &= w_ae^{t_w} \\ h_g &= h_ae^{t_h} \\ \end{aligned} xgygwghg=σ(tx)+xc=σ(ty)+yc=waetw=haeth
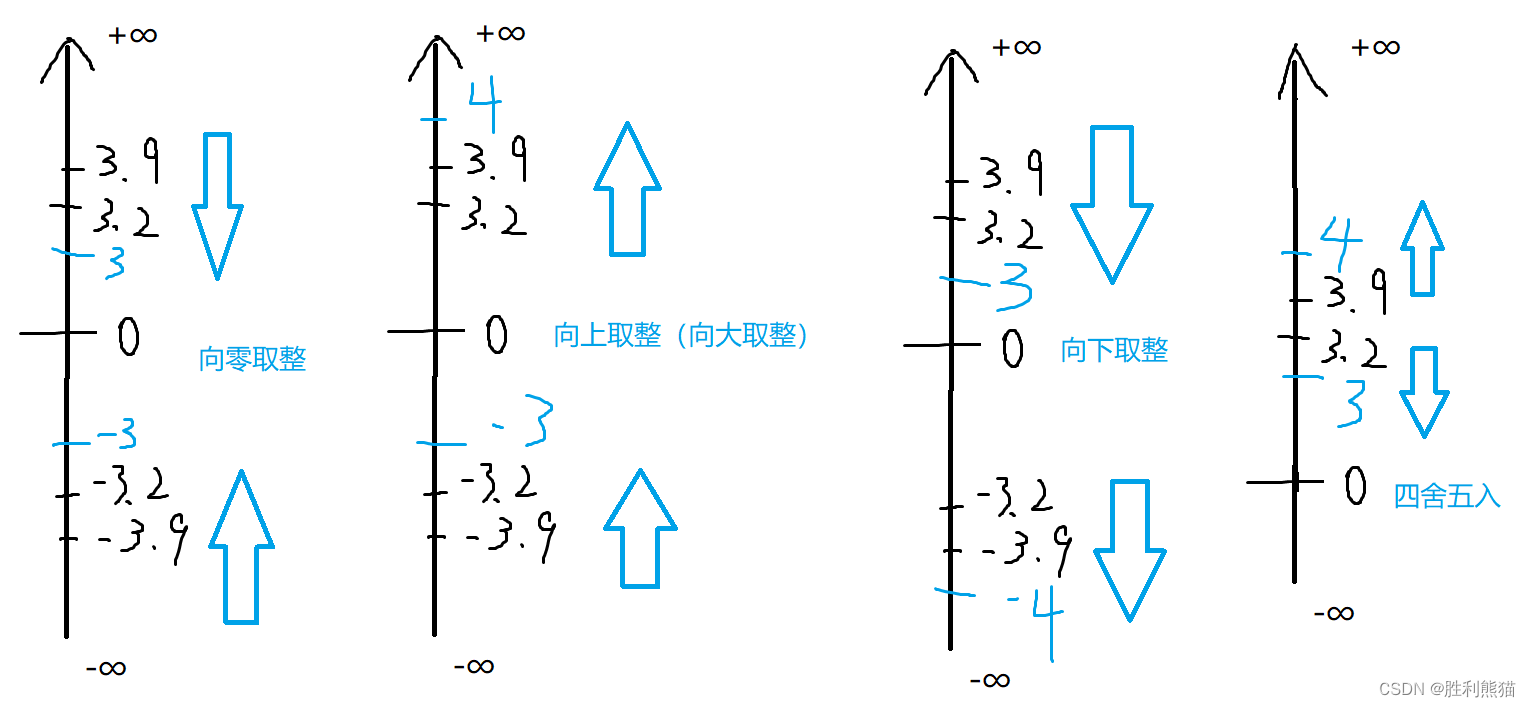
其中 σ ( x ) = 1 / ( 1 + e − x ) \sigma(x) = 1 / (1 + e^{-x}) σ(x)=1/(1+e−x), 函数图像如下
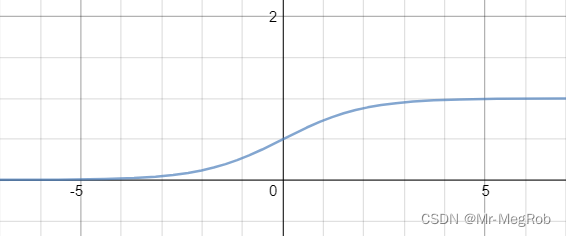
所以 σ ( t x ) ∈ ( 0 , 1 ) \sigma(t_x) \in (0, 1) σ(tx)∈(0,1), σ ( t y ) ∈ ( 0 , 1 ) \sigma(t_y) \in (0, 1) σ(ty)∈(0,1). 这样就将中心点限制在了 grid cell 内部. 而用 e e e 指数则可以保证 w a e t w w_ae^{t_w} waetw 和 h a e t h h_ae^{t_h} haeth 大于 0, 因为 w g w_g wg 和 h g h_g hg 必须大于 0
所以, 我们希望网络的输出 ( t x , t y , t w , t h ) (t_x, t_y, t_w, t_h) (tx,ty,tw,th) 代入上面的公式之后, 能得到或者接近 ( x g , y g , w g , h g ) (x_g, y_g, w_g, h_g) (xg,yg,wg,hg) , 但是 ( t x , t y , t w , t h ) (t_x, t_y, t_w, t_h) (tx,ty,tw,th) 的值要是多少才合适呢?
( x g , y g , w g , h g ) (x_g, y_g, w_g, h_g) (xg,yg,wg,hg), ( x c , y c , w a , h a (x_c, y_c, w_a, h_a (xc,yc,wa,ha) 是已知量, 解上面的等式就可以得到 ( t x , t y , t w , t h ) (t_x, t_y, t_w, t_h) (tx,ty,tw,th),
t x = l n ( x g − x c 1 − x g + c x ) t y = l n ( y g − y c 1 − y g + c y ) t w = l n ( w g w a ) t h = l n ( h g h a ) \begin{aligned} t_x &= ln({{x_g - x_c} \over {1 - x_g + c_x}}) \\ t_y &= ln({{y_g - y_c} \over {1 - y_g + c_y}}) \\ t_w &= ln({w_g \over {w_a}}) \\ t_h &= ln({h_g \over {h_a}}) \\ \end{aligned} txtytwth=ln(1−xg+cxxg−xc)=ln(1−yg+cyyg−yc)=ln(wawg)=ln(hahg)
现在, 解出来的 ( t x , t y , t w , t h ) (t_x, t_y, t_w, t_h) (tx,ty,tw,th) 就是标签值 ( Δ x , Δ y , Δ w , Δ h ) (\Delta x, \Delta y, \Delta w, \Delta h) (Δx,Δy,Δw,Δh)
x c , y c x_c, y_c xc,yc 有必要要另外说明一下, 两个都是整数, 因为它们是 grid cell 的坐标, 范围是 [ 0 , [0, [0, 特征图尺寸 − 1 ] - 1] −1], 如果哪一个 grid cell 中的 anchor box 负责预测目标, 那么这个 anchor box 的一部分坐标就已知了, 剩下的就是预测这个 anchor box 的中心坐标相对于这个 grid cell 左上角坐标 ( x c , y c ) (x_c, y_c) (xc,yc) 的偏移量.
还是以上面的图用具体的数字来说明, 假设上面的图是 52 × 52 52 \times 52 52×52 的特征图对应的原图, 那一个格子宽度是 8 个像素, 一个格子对应特征图一个 grid cell, 此时 ground truth 绝对坐标是 ( 18.82 , 12.98 , 17 , 20 ) (18.82, 12.98, 17, 20) (18.82,12.98,17,20), anchor box 的尺寸是 ( 16 , 22 ) (16, 22) (16,22). 从图中可以看到 c x = 2 , c y = 1 c_x = 2, c_y = 1 cx=2,cy=1, 则 σ ( Δ x ) = 0.3525 , σ ( Δ y ) = 0.6225 \sigma(\Delta x) = 0.3525, \sigma(\Delta y) = 0.6225 σ(Δx)=0.3525,σ(Δy)=0.6225, 0.3525 0.3525 0.3525 和 0.6225 0.6225 0.6225 这两个数字怎么来的?
因为 ground truth 中心点绝对坐标是 ( 18.82 , 12.98 ) (18.82, 12.98) (18.82,12.98), 相对于 grid cell 左上角的坐标是
( 18.82 − 8 x c , 12.98 − 8 y c ) = ( 2.82 , 4.98 ) (18.82 - 8x_c, 12.98 - 8y_c) = (2.82, 4.98) (18.82−8xc,12.98−8yc)=(2.82,4.98)
再将 ( 2.82 , 4.98 ) (2.82, 4.98) (2.82,4.98) 以步长 8 8 8 为分母归一化得到 ( 0.3525 , 0.6225 ) (0.3525, 0.6225) (0.3525,0.6225), 所以 ground truth 归一化后的中心坐标为 ( 2.3525 , 1.6225 ) (2.3525, 1.6225) (2.3525,1.6225), 公式中的 ( x g , y g ) (x_g, y_g) (xg,yg) 就是归一化后的坐标. 如果要还原成绝对坐标, 将 ( 2.3525 , 1.6225 ) (2.3525, 1.6225) (2.3525,1.6225) 乘以 8 8 8 就可以得到 ( 18.82 , 12.98 ) (18.82, 12.98) (18.82,12.98)
反解 σ ( Δ x ) = 0.3525 , σ ( Δ y ) = 0.6225 \sigma(\Delta x) = 0.3525, \sigma(\Delta y) = 0.6225 σ(Δx)=0.3525,σ(Δy)=0.6225, 再将 w g , h g , w a , h a w_g, h_g, w_a, h_a wg,hg,wa,ha 再入
Δ w = l n ( w g w a ) Δ h = l n ( h g h a ) \begin{aligned} \Delta w &= ln({w_g \over {w_a}}) \\ \Delta h &= ln({h_g \over {h_a}}) \\ \end{aligned} ΔwΔh=ln(wawg)=ln(hahg)
将就可以解出 ( Δ x , Δ y , Δ w , Δ h ) = ( − 0.608068 , 0.500173 , 0.060625 , − 0.095310 ) (\Delta x, \Delta y, \Delta w, \Delta h) = (-0.608068, 0.500173, 0.060625, -0.095310) (Δx,Δy,Δw,Δh)=(−0.608068,0.500173,0.060625,−0.095310), 所以这个 anchor box 的关于位置的标签值就是 ( − 0.608068 , 0.500173 , 0.060625 , − 0.095310 ) (-0.608068, 0.500173, 0.060625, -0.095310) (−0.608068,0.500173,0.060625,−0.095310)
其实将 σ ( Δ x ) \sigma(\Delta x) σ(Δx) 与 σ ( Δ y ) \sigma(\Delta y) σ(Δy) 限制在 ( 0 , 1 ) (0, 1) (0,1) 是有一点问题的, 因为 Δ x \Delta x Δx 和 Δ y \Delta y Δy 趋于 − ∞ -\infty −∞ 时 σ ( x ) \sigma(x) σ(x) 才能取到 0 0 0, 趋于 + ∞ +\infty +∞ 时 σ ( x ) \sigma(x) σ(x) 才能取到 1 1 1. 所以当 ground truth 中心点在 grid cell 边界的时候是学习不到这个值的. 不过这个也不是什么大问题, 当 ∣ t x ∣ |t_x| ∣tx∣ 和 ∣ t y ∣ |t_y| ∣ty∣ 大于 5 5 5 后, 就已经很接近了. 但是打标签会有问题, 因为按上面的公式计算出来的值是 − ∞ -\infty −∞ 或者 + ∞ +\infty +∞. 为了解决一个问题, 可以有两种方法, 一是打标签的时候, 把标签值的绝对值限制在某个范围内, 比如 5 5 5, σ ( 5 ) = 0.9933071491 \sigma(5)=0.9933071491 σ(5)=0.9933071491, 算是一个比较接近的数了. 另一个更好的方法是在 将 σ ( x ) \sigma(x) σ(x) 修改成
k σ ( x ) − b k\sigma(x) -b kσ(x)−b
其中 k > 1 , b > 0 k > 1, b > 0 k>1,b>0. 假设 k = 2 , b = 0.5 k = 2, b = 0.5 k=2,b=0.5, 这样的话, 假设 2 σ ( Δ x ) − 0.5 = 0.99 2\sigma(\Delta x) - 0.5 = 0.99 2σ(Δx)−0.5=0.99, 则标签值 Δ x = 1.072120 \Delta x = 1.072120 Δx=1.072120, 假设 2 σ ( Δ x ) − 0.5 = 0.01 2\sigma(\Delta x) - 0.5 = 0.01 2σ(Δx)−0.5=0.01, 则标签值 Δ x = − 1.072120 \Delta x = -1.072120 Δx=−1.072120, 这很合理. 这就是在 YOLO v4 中的改进方法, 本文就选这种方法修正这个问题
3.4 类别标签怎么填?
这个很简单, 20 20 20 个类别, 只要按 one-hot 编码填进去就可以了, 在 3.2 3.2 3.2 节的图中就是一个例子
3.5 置信度标签怎么填?
这个更简单, 如果是负样本填 0 0 0, 正样本就填 1 1 1, 忽略的样本呢? 这个看你的心情了, 只要不是 0 0 0 或者 1 1 1 就行, 为了更好的区分, 我就填 − 1 -1 −1
四. 打标签代码
既然要为 anchor box 打标签, 那首先要生成 anchor box
# 生成 anchor box 函数
# image_size: 图像尺寸
# anchor_size: 聚类生成的 anchor box 尺寸
def create_anchors(image_size, anchor_size):# 生成基础的 k 个 anchor boxbase_anchors = []for s in anchor_size:base_anchors.append((-s[0] // 2, -s[1] // 2, s[0] // 2, s[1] // 2))grid_anchors = len(anchor_size) // 3 # 每个特征图中一个 grid cell 包含的 anchor box 的数量anchor_boxes = [] # 存放各特征图生成的 anchor box 的列表# 生成三种尺寸特征图的 anchor boxfor i, stride in enumerate(STRIDES):# 特征图尺寸feature_rows = image_size[0] // stridefeature_cols = image_size[1] // stride# 中心坐标ax = (tf.cast(tf.range(feature_cols), tf.float32)) * stride + stride // 2ay = (tf.cast(tf.range(feature_rows), tf.float32)) * stride + stride // 2ax, ay = tf.meshgrid(ax, ay)# 变换形状方便下面的 tf.stackax = tf.reshape(ax, (-1, 1))ay = tf.reshape(ay, (-1, 1))# stack([ax, ay, ax, ay]) 成这样的格式, 是为了分别加上 base_anchor 的左上角坐标和右下角坐标boxes = tf.stack([ax, ay, ax, ay], axis = -1)# boxes: (x1, y1, x2, y2) = 中心坐标 + base_anchors, 一种尺寸的特征图取 3 个 anchor box boxes = boxes + base_anchors[i * grid_anchors: i * grid_anchors + grid_anchors]anchor_boxes.append(boxes)# 将三个特征图的 anchor box 放到一个 Tensor 中, 最后 shape == (n, 4)feature_boxes = tf.concat([anchor_boxes[0], anchor_boxes[1], anchor_boxes[2]], axis = 0)feature_boxes = tf.reshape(feature_boxes, (-1, 4))return feature_boxes
测试 create_anchors 函数
# 测试 create_anchors 函数
anchor_boxes = create_anchors((LONG_SIDE, LONG_SIDE), cluster_anchors)
print(anchor_boxes)
打印结果
tf.Tensor(
[[ -4. -7. 12. 15.][ -9. -25. 17. 33.][-20. -13. 28. 21.]...[277. 333. 522. 467.][322. 286. 478. 514.][245. 268. 555. 531.]], shape=(10647, 4), dtype=float32)
因为打标签时会用到 I o U IoU IoU, 所以先定义一个函数计算 I o U IoU IoU
# 计算 IoU 函数
# gt_box: 一个标注框
# anchor_boxes: n 个 anchor box, shape = (n, 4)
def get_iou(gt_box, anchor_boxes):x = tf.maximum(gt_box[0], anchor_boxes[:, 0])y = tf.maximum(gt_box[1], anchor_boxes[:, 1])w = tf.maximum(tf.minimum(gt_box[2], anchor_boxes[:, 2]) - x, 0)h = tf.maximum(tf.minimum(gt_box[3], anchor_boxes[:, 3]) - y, 0)intersection = w * hgt_area = (gt_box[2] - gt_box[0]) * (gt_box[3] - gt_box[1])box_area = (anchor_boxes[:, 2] - anchor_boxes[:, 0]) * (anchor_boxes[:, 3] - anchor_boxes[:, 1])union = gt_area + box_area - intersectionious = intersection / unionreturn tf.reshape(ious, (-1, 1))
测试 I o U IoU IoU
# 测试 IoU
a = (8, 8, 32, 64)
b = [(3, 3, 32, 65), (6, 3, 35, 70), (20, 15, 40, 70), (80, 100, 128, 160)]
print("iou(a, b) =", get_iou(a, np.array(b)))
测试结果
iou(a, b) = tf.Tensor(
[[0.74749722][0.69171384][0.31681034][0. ]], shape=(4, 1), dtype=float64)
在打位置标签 ( Δ x , Δ y , Δ w , Δ h ) (\Delta x, \Delta y, \Delta w, \Delta h) (Δx,Δy,Δw,Δh) 的时候, 需要作一些计算, 我们把这些计算也放到一个函数中去方便使用
# 位置标签函数
# gt_box: 一个标注框
# anchor_boxes: 一张图中所有 anchor box
def get_delta(gt_box, anchor_boxes):# 返回值, 返回一个 gt_box 与所有 anchor box 之间的修正量# 计算时把所有的 anchor box 当成正样本, 后面会根据 IoU 筛选出真正的正样本deltas = None# gt_box 在原图中的 (x, y, w, h) 形式坐标gt_x = (gt_box[0] + gt_box[2]) * 0.5gt_y = (gt_box[1] + gt_box[3]) * 0.5gt_w = (gt_box[2] - gt_box[0])gt_h = (gt_box[3] - gt_box[1])# anchor box 在原图中的宽和高a_w = anchor_boxes[..., 2] - anchor_boxes[..., 0]a_h = anchor_boxes[..., 3] - anchor_boxes[..., 1]# 每种特征图的 anchor box 数量 (52 × 52 × 3, 26 × 26 × 3, 13 × 13 × 3)anchor_num = [(LONG_SIDE // s) * (LONG_SIDE // s) * 3 for s in STRIDES]# 不同特征图 anchor box 切片索引idx_start = 0idx_end = anchor_num[0]for i in (0, 1, 2):# gt_box 中心点在特征图中距 grid cell 左上角的距离dist_x = tf.constant(gt_x / STRIDES[i] - round(gt_x) // STRIDES[i],shape = (anchor_num[i],), dtype = tf.float32)dist_y = tf.constant(gt_y / STRIDES[i] - round(gt_y) // STRIDES[i],shape = (anchor_num[i],), dtype = tf.float32)# 坐标计算公式为 2 * sigma(x) - 0.5delta_x = tf.math.log((0.5 + dist_x) / (1.5 - dist_x))delta_y = tf.math.log((0.5 + dist_y) / (1.5 - dist_y))# 每个尺寸的特征图的 anchor box 数量不一样, 所以要加以区分delta_w = tf.math.log(gt_w / a_w[idx_start: idx_end])delta_h = tf.math.log(gt_h / a_h[idx_start: idx_end])idx_start = idx_endidx_end = idx_end + (anchor_num[i + 1] if i < 2 else sum(anchor_num))if None == deltas:deltas = tf.stack([delta_x, delta_y, delta_w, delta_h], axis = -1)else:deltas = tf.concat([deltas, tf.stack([delta_x, delta_y, delta_w, delta_h], axis = -1)], axis = 0)return deltas
为了方便计算, get_delta 在函数内部我们假设所有的 anchor box 都是正样本, 这样计算也不影响, 因为损失函数中我们只关心真正的正样本, 至于其他样本是什么值并不影响
因为只有 ground truth 中心所在的 grid cell 中的 k k k 个 anchor box 才负责预测, 所以我们要把这 k k k 个 anchor box 的序号找出来, 方便后面函数的操作
# 计算 ground truth 所在 grid cell 的 k 个 anchor box 的序号
# 一共有 10647 个, 返回的是在三个特征图中的位置序号
def get_valid_idx(gt_box):# 每种特征图的 anchor box 数量 (52 × 52 × 3, 26 × 26 × 3, 13 × 13 × 3)anchor_num = [(LONG_SIDE // s) * (LONG_SIDE // s) * 3 for s in STRIDES]# 一个 grid cell 中的 anchor box 数量grid_anchors = (CLUSTER_K // 3)# gt_box 在原图的中心坐标x = (gt_box[0] + gt_box[2]) * 0.5y = (gt_box[1] + gt_box[3]) * 0.5# 后面的特征图中 anchor box 的序号要加上前面的特征图的总的 anchor box 的数量offset = [0, anchor_num[0], anchor_num[0] + anchor_num[1]]# 返回值ret_idx = []for i in (0, 1, 2):grid_x = round(x) // STRIDES[i]grid_y = round(y) // STRIDES[i]# 在各特征图中的起始序号idx_start = grid_y * (LONG_SIDE // STRIDES[i]) * grid_anchors + grid_x * grid_anchors + offset[i]ret_idx.append(idx_start)# 后面 grid_anchors - 1 个 anchor box 序号顺序增加for j in range(1, grid_anchors):ret_idx.append(ret_idx[-1] + 1)return ret_idx
# 测试 get_valid_idx 函数
valid_boxes = get_valid_idx((0, 0, 8, 8))
print(valid_boxes)
输出结果
[0, 1, 2, 8112, 8113, 8114, 10140, 10141, 10142]
现在定义一个函数, 为一张图像的 anchor box 打标签
# 定义打标签函数
# gts: get_ground_truth 函数的第三个返回值, 前两个在这里用不上, 所以下面的循环中只用了最后一个
# anchor_boxes: create_anchors 函数生成的 anchor box
def get_label(gts, anchor_boxes):# 总的 anchor box 数量anchor_nums = anchor_boxes.shape[0]# 类别数量categories = len(CATEGORIES)# 位置标签(Δx,Δy,Δw,Δh), 全部初始化为 0deltas = tf.zeros((anchor_nums, 4), dtype = tf.float32)# 各 gt_box 与 anchor box 的最大 IoU, 要比较各 gt_box 与所有 anchor box IoU 的大小# 把最大值记录下来, 这样将标签分配给最合适的 anchor box, 还有一个功能是用来判断是否是负样本max_ious = tf.zeros((anchor_nums, 1), dtype = tf.float32)# 类别标签, 全部初始化为 0cls_ids = tf.zeros((anchor_nums, categories), dtype = tf.float32)# 置信度标签, 全部初始化为 -1, 表示忽略样本confidence = tf.fill((anchor_nums, 1), -1.0)for gt_box, cls_id in gts[-1]:# 所有 anchor box 的可用状态, 只有 gt_box 所在 grid cell 的 k 个 anchor box 可用, 先全部初始化为 Falsevalid_mask = tf.fill((anchor_nums, 1), False)# 取出 gt_box 所在 grid cell 的 k 个 anchor box 的序号indices = get_valid_idx(gt_box)indices = tf.reshape(tf.constant(indices), (-1, 1))updates = tf.constant(True, shape = indices.shape)# 将序号位置的 False 变成 Truevalid_mask = tf.tensor_scatter_nd_update(valid_mask, indices, updates)# 正常计算 IoU# ious = get_iou(gt_box, anchor_boxes)# 聚类方式计算 IoU, gt_box 与 所有 anchor box 的 IoU, 左上角都在 (0, 0)ious = cluster_iou((gt_box[2] - gt_box[0], gt_box[3] - gt_box[1]),tf.stack([anchor_boxes[:, 2] - anchor_boxes[:, 0],anchor_boxes[:, 3] - anchor_boxes[:, 1]], axis = -1))# 聚类方式计算 IoU 结果要变换到合适的 shapeious = tf.reshape(ious, (anchor_nums, -1))# 屏蔽掉其他 grid cell 的 IoUious = tf.where(valid_mask, ious, 0.0)# 找出最大值所在的位置grater_mask = ious > max_ious# 记录每次比较的最大值, 这个是在不同的 gt_box 这间比较max_ious = tf.maximum(ious, max_ious)# 获取当前 gt_box 与 anchor box IoU 最大值和对应的索引,# k = 1, 表示我们只关心最大的一个, 这个也许是小于阈值的, 但是我们也要将其变成正样本_, indices = tf.math.top_k(tf.reshape(ious, (anchor_nums, )), k = 1) # 创建掩码, 只有最大值位置为 True, 其他为 Falsemax_mask = tf.cast(tf.one_hot(indices, depth = anchor_nums), dtype = tf.bool)max_mask = tf.reshape(max_mask, (-1, 1))# 将 IoU >= POS_THRES 的也标记成 True, 这样可以增加正样本数量, 再将 max_mask 加入到 pos_maskpos_mask = ious >= POS_THRESpos_mask = tf.logical_or(max_mask, pos_mask)# 与 grater_mask 做 and 是因为当前 gt_box 匹配的 IoU 要大于之前匹配的# 才能变更这个 anchor box 的标签, 要不然就是之前的标签更合适pos_mask = tf.logical_and(pos_mask, grater_mask)# 将 deltas 正样本位置替换成计算好的标签值deltas = tf.where(pos_mask, get_delta(gt_box, anchor_boxes), deltas)# 当前 gt_box 的整数类别转换成 one-hotone_hot = tf.reshape(tf.one_hot(cls_id, depth = categories), (-1, 20))# 将 cls_ids 对应位置替换成当前 gt_box 的 one-hot 标签cls_ids = tf.where(pos_mask, one_hot, cls_ids)# 将正样本位置置信度替换成 1confidence = tf.where(pos_mask, 1.0, confidence)# 循环完成后, confidence 中只有正样本和忽略样本, 还没有负样本# 找出 confidence 所有正样本的位置pos_mask = confidence > 0# 由 max_ious 定位出所有小于阈值的位置neg_mask = max_ious < NEG_THRES# 从 neg_mask 中去除 pos_mask 位置neg_mask = tf.where(pos_mask, False, neg_mask)# 将负样本位置的值替换成 0confidence = tf.where(neg_mask, 0.0, confidence)# 组合成总的标签信息# 现在 label 的格式为 (位置标签, 类别标签, 置信度), shape = (10647 × 25)# 如果 reshape 可变成 75 个通道, 只是这样就要分成三个 tensor 了, 没有必要label = tf.concat([deltas, cls_ids, confidence], axis = -1)# 最后返回 max_ious 是不需要的, 只是为了查看每个 ancor box 与 ground truth 的 IoUreturn label
测试函数
# 测试打标签函数
gts = get_ground_truth(label_data[1], label_data[2], CATEGORIES)
label = get_label(gts, anchor_boxes)
# 找出最后一维值为 1 的行, 也就是正样本
pos_mask = tf.equal(label[:, -1], 1)
pos_targets = tf.boolean_mask(label, pos_mask)
print(pos_targets)
输出结果
tf.Tensor(
[[-0.6466271 0. 0.09909087 0.38566247 1. 0.0. 0. 0. 0. 0. 0.0. 0. 0. 0. 0. 0.0. 0. 0. 0. 0. 0.1. ][-1.0986123 0.2513144 0.08004274 0.38566247 1. 0.0. 0. 0. 0. 0. 0.0. 0. 0. 0. 0. 0.0. 0. 0. 0. 0. 0.1. ][-0.3794896 0.7884574 0.01869218 -0.44055638 1. 0.0. 0. 0. 0. 0. 0.0. 0. 0. 0. 0. 0.0. 0. 0. 0. 0. 0.1. ][-0.6466271 0.12516314 0.01869218 -0.44055638 1. 0.0. 0. 0. 0. 0. 0.0. 0. 0. 0. 0. 0.0. 0. 0. 0. 0. 0.1. ][-0.8622235 -0.18805222 0. -0.42285687 1. 0.0. 0. 0. 0. 0. 0.0. 0. 0. 0. 0. 0.0. 0. 0. 0. 0. 0.1. ][ 0.06252041 -0.2513144 0.03704124 -0.5146644 1. 0.0. 0. 0. 0. 0. 0.0. 0. 0. 0. 0. 0.0. 0. 0. 0. 0. 0.1. ]], shape=(6, 25), dtype=float32)
找到 6 6 6 个正样本, 将它们画到原图上
# 将找出来的正样本 anchor box 显示到原图, gt_box 已经在前面画过了
indices = tf.where(tf.equal(label[:, -1], 1.0))
for t in indices:t = t.numpy()[0]box = anchor_boxes[t].numpy()print(box)cv.rectangle(img_copy, (round(box[0]), round(box[1])), (round(box[2]), round(box[3])),(0, 0, random.randint(128, 256)), 2)plt.figure("label_box", figsize = (8, 4))
plt.imshow(img_copy[..., : : -1])
plt.show()
[ 44. 203. 92. 237.]
[ 60. 275. 108. 309.]
[333. 60. 386. 147.]
[141. 76. 194. 163.]
[ 29. 92. 82. 179.]
[157. 172. 210. 259.]

五. 代码下载
示例代码可下载 Jupyter Notebook 示例代码
上一篇: 保姆级 Keras 实现 YOLO v3 二
下一篇: 保姆级 Keras 实现 YOLO v3 四 (待续…)
相关文章:

保姆级 Keras 实现 YOLO v3 三
保姆级 Keras 实现 YOLO v3 三 一. 分配 anchor box二. 正负样本匹配规则三. 为每一个 anchor box 打标签3.1 anchor box 长什么样?3.2 每一个 anchor box 标签需要填充的信息有哪些?3.3 ( Δ x , Δ y , Δ w , Δ h ) (\Delta x, \Delta y, \Delta w, \Delta h) (Δx,Δy,…...
HPM6750系列--第十篇 时钟系统
一、目的 上一篇中《HPM6750系列--第九篇 GPIO详解(基本操作)》我们讲解了HPM6750 GPIO相关内容,再进一步讲解其他外设功能之前,我们有必要先讲解一下时钟系统。 时钟可以说是微控制器系统中的心脏,外设必须依赖时钟才…...
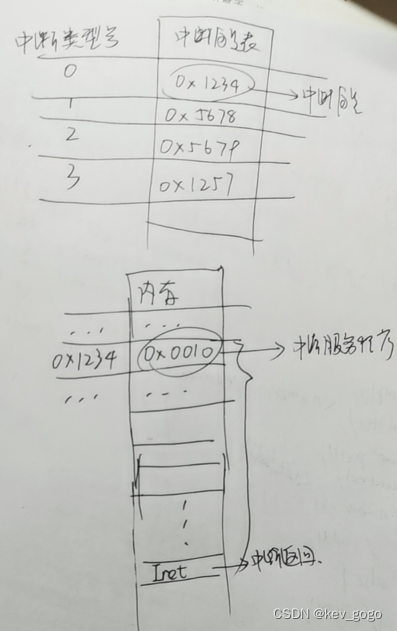
【简单总结】中断类型号 中断向量 中断入口地址
通过中断类型号可以计算出中断向量的地址。 然后根据该地址可以在中断向量表中取出中断服务程序的入口地址(中断向量)。 而中断向量就是中断服务程序入口地址。 做个不严谨的图: 1:通过中断类型号找到中断向量 2:通…...

【Python百宝箱】从传感器到云端:深度解析Python在物联网中的多面应用
迈向智能未来:Python与物联网生态系统的完美融合 前言 随着物联网技术的不断发展,Python作为一种灵活且强大的编程语言,逐渐成为物联网开发的重要工具之一。本文将深入探讨物联网领域中常用的Python库和框架,涵盖了从轻量级通信…...
)
weston 1: 编译与运行傻瓜教程(补充)
系统kubuntu23.10 git clone https://gitlab.freedesktop.org/wayland/wayland.git 86588fbdebe7f6ac9363d98f524e4ae14bd4b019 meson build/ --prefix$WLD ninja -C build/ install git clone https://gitlab.freedesktop.org/wayland/wayland-protocols.git c4f559866f13…...

微服务保护--线程隔离(舱壁模式)
一、线程隔离的实现方式 线程隔离有两种方式实现: 线程池隔离 信号量隔离(Sentinel默认采用) 如图: 线程池隔离:给每个服务调用业务分配一个线程池,利用线程池本身实现隔离效果 信号量隔离:…...
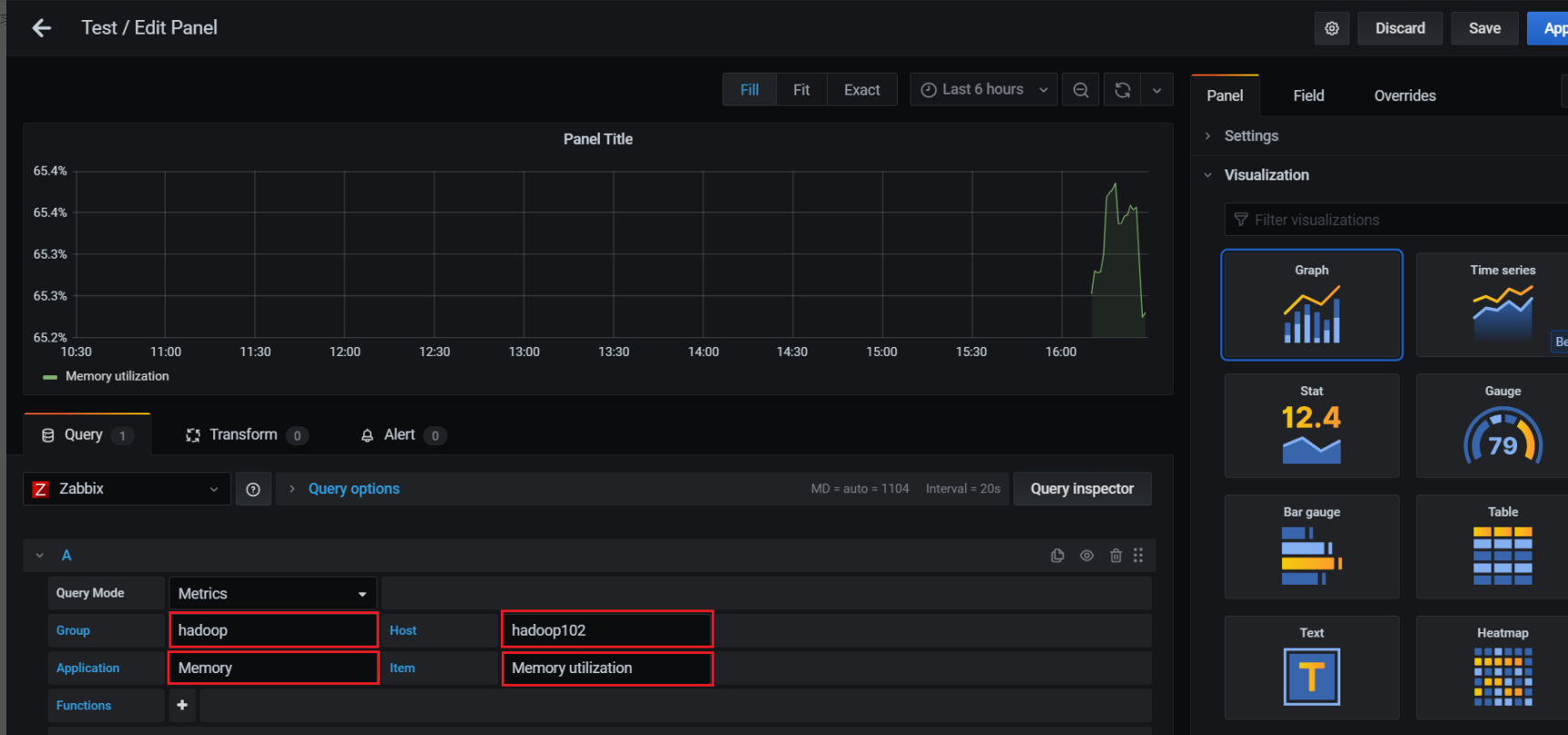
集群监控Zabbix和Prometheus
文章目录 一、Zabbix入门概述1、Zabbix概述2、Zabbix 基础架构3、Zabbix部署3.1 前提环境准备3.2 安装Zabbix3.3 配置Zabbix3.4 启动停止Zabbix 二、Zabbix的使用与集成1、Zabbix常用术语2、Zabbix实战2.1 创建Host2.2 创建监控项(Items)2.3 创建触发器&…...
—污点、容忍)
K8S(七)—污点、容忍
目录 污点、容忍污点(Taints):容忍(Tolerations):如何一起使用污点和容忍:操作符(Equal、Exists)例子基于污点的驱逐基于节点状态添加污点 污点、容忍 官网地址…...

新视野大学英语1 词组 12.17
embarrassment和awkwardness的区别以及各自的组词。 "Embarrassment" 和 "awkwardness" 都可以用来描述一种尴尬或不舒服的感觉,但它们有一些微妙的区别。 "Embarrassment" 指的是由于尴尬、困窘或难堪的情况而产生的感觉。 这种感觉…...

springboot实战项目之使用AOP技术实现各种角色的鉴权功能
前言 项目开发需求,会员有不同的角色,不同的角色被赋予不同的权限,这就需要对会员的操作进行鉴权处理。 方案 采用aop,可实现满足这种需求,创建匿名类。对外提供接口的时候都会拦截,这种会有弊端&#x…...
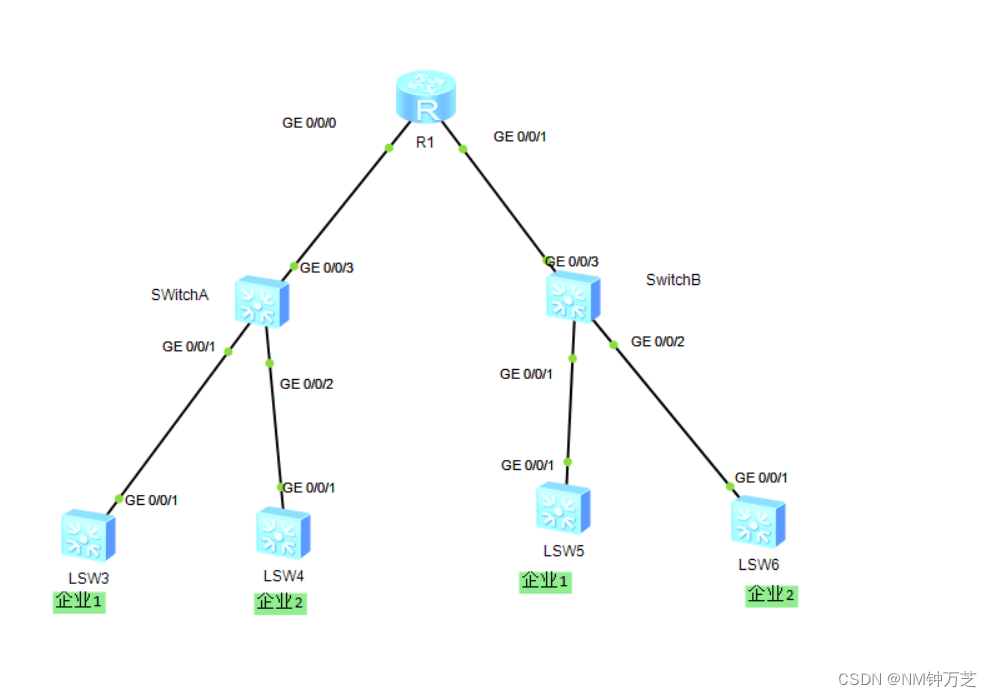
华为配置基本QinQ示例
组网需求 如图1所示,网络中有两个企业,企业1有两个分支,企业2有两个分支。这两个企业的各办公地的企业网都分别和运营商网络中的SwitchA和SwitchB相连,且公网中存在其它厂商设备,其外层VLAN Tag的TPID值为0x9100。 现…...

【漏洞复现】系列集合
该篇文章仅供学习网络安全技术参考研究使用,请勿使用相关技术做违法操作 Apache Apache_HTTPD_未知后缀名解析Apache_HTTPD_换行解析(CVE-2017-15715)Apache_HTTPD_多后缀解析Apache_HTTP_2.4.50_路径穿越(CVE-2021-42013)Apache_HTTP_2.4.49_路径穿越(CVE-2021-41…...
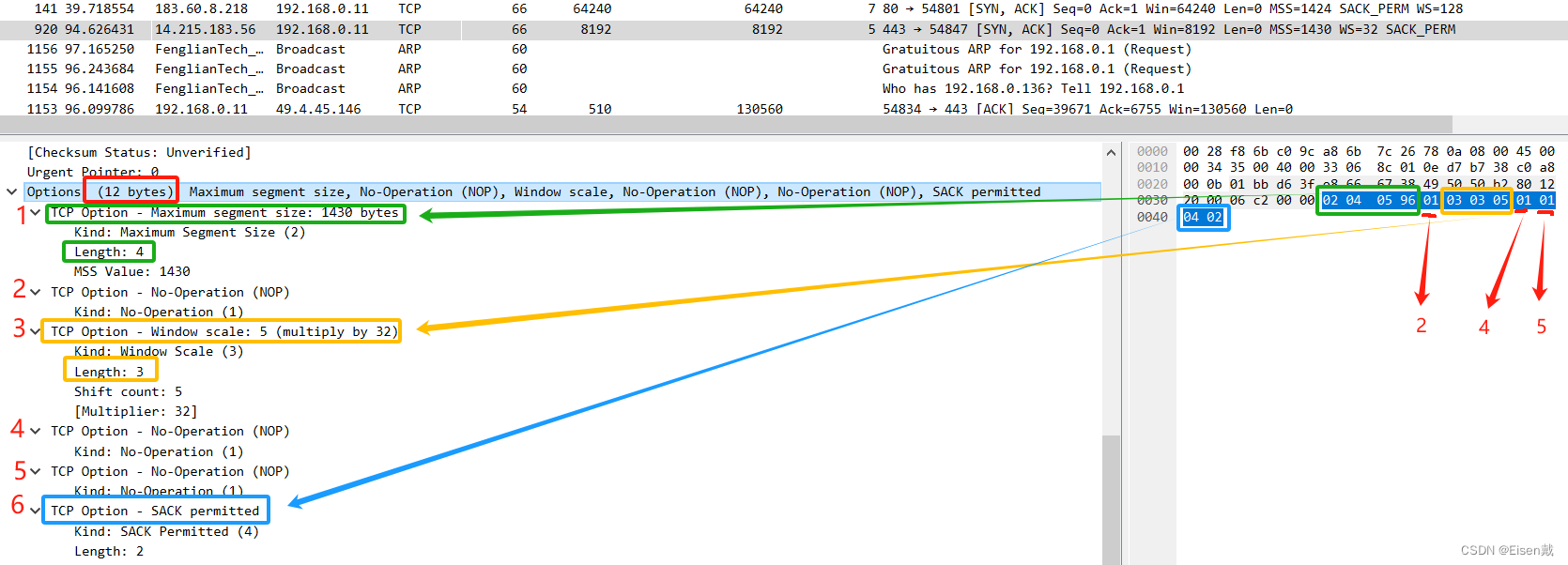
TCP报文头(首部)详解
本篇文章基于 RFC 9293: Transmission Control Protocol (TCP) 对TCP报头进行讲解,部分内容会与旧版本有些许区别。 TCP协议传输的数据单元是报文段,一个报文段由TCP首部(报文头)和TCP数据两部分组成,其中TCP首部尤其重…...

第4章-第1节-初识Java的数组
1、数组 属于Java内存层面的一款容器(crud操作)。 概念: 内存中的一块存储区域(空间),内部有一组连续的小区域(元素空间),有数据类型的限定,可以存入一组匹配类型的数据,并且根据需要可以改动元素空间中的数据内…...
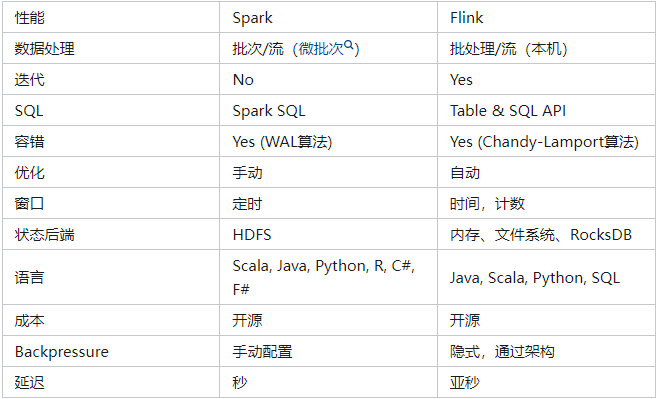
大数据技术10:Flink从入门到精通
导语:前期入门Flink时,可以直接编写通过idea编写Flink程序,然后直接运行main方法,无需搭建环境。我碰到许多初次接触Flink的同学,被各种环境搭建、提交作业、复杂概念给劝退了。前期最好的入门方式就是直接上手写代码&…...
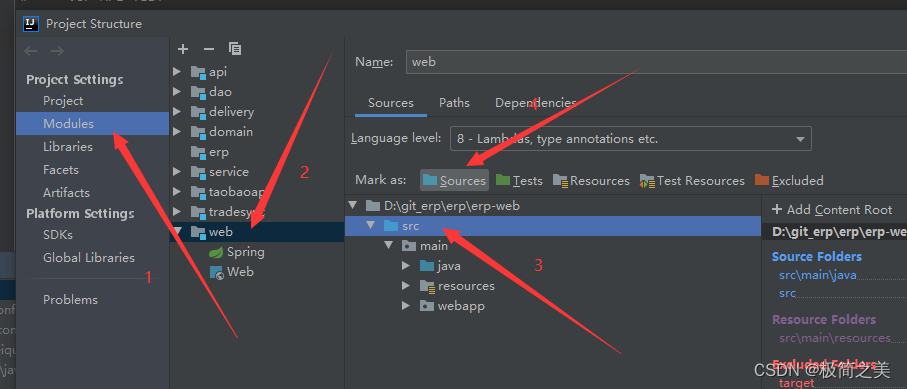
IDEA中工具条中的debug按钮不能用了显示灰色
IDEA中工具条中的debug按钮不能用了显示灰色 1. 问题描述 IDEA上的DEBUG按钮突然变成了灰色: 2. 解决办法 一通搜索,终于找到解决办法 点击 File -> Project Structure如下图操作 3. 重启,解决 4. 参考 https://www.cnblogs.com…...
【MySQL内置函数】
目录: 前言一、日期函数获取日期获取时间获取时间戳在日期上增加时间在日期上减去时间计算两个日期相差多少天当前时间案例:留言板 二、字符串函数查看字符串字符集字符串连接查找字符串大小写转换子串提取字符串长度字符串替换字符串比较消除左右空格案…...
C++相关闲碎记录(14)
1、数值算法 (1)运算后产生结果accumulate() #include "algostuff.hpp"using namespace std;int main() {vector<int> coll;INSERT_ELEMENTS(coll, 1, 9);PRINT_ELEMENTS(coll);cout << "sum: " << accumulate(…...
:菜单权限,按钮权限,打包,发布nginx)
18、vue3(十八):菜单权限,按钮权限,打包,发布nginx
目录 一、菜单权限和路由拆分 1.思路分析 2.深拷贝插件 3.代码实现 4.效果展示...

04 在Vue3中使用setup语法糖
概述 Starting from Vue 3.0, Vue introduces a new syntactic sugar setup attribute for the <script> tag. This attribute allows you to write code using Composition API (which we will discuss further in Chapter 5, The Composition API) in SFCs and shorte…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
