在排序数组中查找元素的第一个和最后一个位置(Java详解)
一、题目描述
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例:
输入:nums = [5,7,7,8,8,10],target = 8
输出:[3, 4]
输入:nums = [5,7,7,8,8,10],target = 6
输出:[-1, -1]
输入:nums = [ ],target = 0
输出:[-1, -1]

二、题解
思路分析:
题目要求我们找到出现target的第一个位置和最后一个位置,首先,我们想到可以通过暴力枚举的方法来解决该问题,即遍历数组,并记录target第一次出现和最后一次出现的位置。然而,题目要求我们实现时间复杂度为O(log n)的算法,且题目中给出的数组为非递减的数组,因此,我们可以考虑使用二分查找的方法来解决该问题
由于题目中数据量较小,使用遍历的方法也可以通过该题
遍历代码:
class Solution {public int[] searchRange(int[] nums, int target) {int first = -1;int last = -1;boolean flg = false;//判断是否是第一个位置for (int i = 0; i < nums.length; i++) {//第一个位置if(nums[i] == target && !flg){first = i;flg = true;}//最后一个位置//注意处理特殊情况,即最后一个元素在最后一个位置时,nums[i+1]越界if(nums[i] == target && (i == nums.length - 1 || nums[i+1] != target)){last = i;}}int[] ret = {first,last};return ret;}
}如何使用二分查找来解决该问题?
题目要求我们找到target在数组中第一次出现和最后一次出现的位置,利用数组非递减的性质
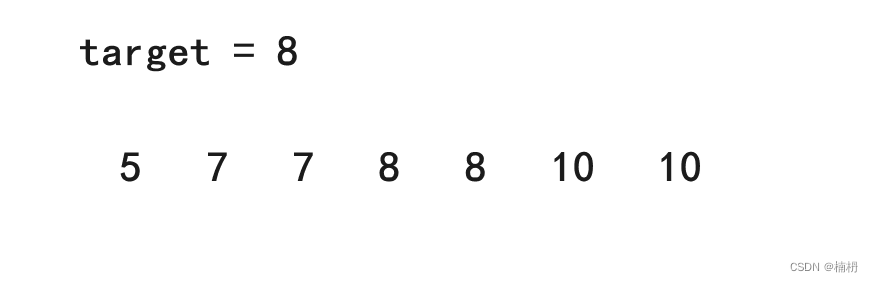
首先我们查找元素的第一个位置:
我们可通过target将数组分为两部分:

其中,左边部分为小于target的元素,右边部分为大于等于target的元素,由于右边区域大于等于target,因此右边区域最左边的值即为target第一次出现的位置,即右边区域的左端点为所求结果

我们定义left指向0位置,right指向最后一个元素,mid指向中间位置

若mid指向的元素落在右边区间,此时nums[mid]大于等于target,需要更新right的值,由于要找的结果(target第一次出现的位置)在此区间内,即mid所指向的位置可能就是最终结果,因此不能将right更新为mid - 1,而应更新为mid
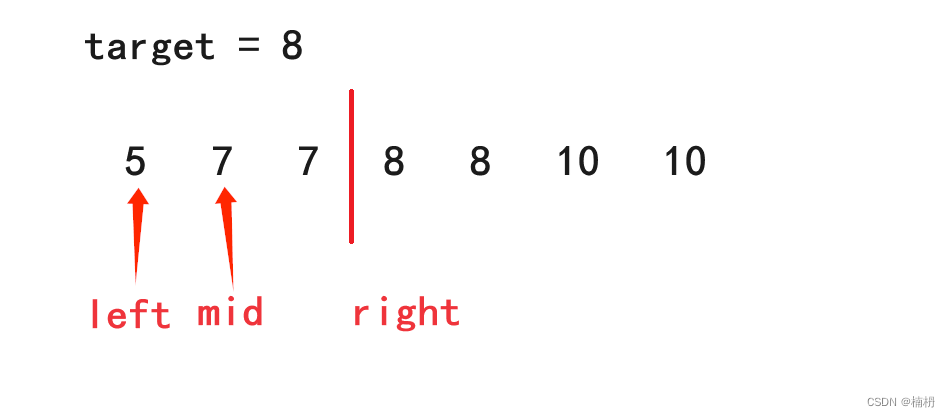
若mid所指向的元素落在左边区间,此时nums[mid]小于target,需要更新 left 的值,由于要找的结果不在此区间内,因此可将left的结果更新为 mid + 1

当left和right之间元素为偶数个时,此时中间元素有两个,应该选择哪一个作为中间元素?
由于我们查找的是右边区间内最左边的元素,因此,应该选择左边的元素作为中间元素
若选择右边元素作为中间元素,能够成功查找到结果吗?
当选择右边元素作为中间元素时,此时会出现死循环的情况,例如:
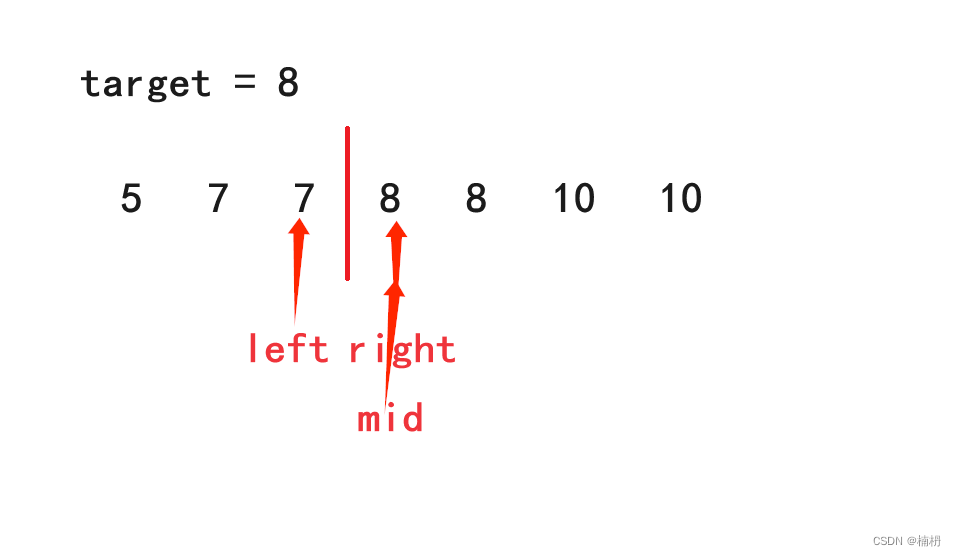 上图中,当选择右边元素作为中间元素时,mid指向的元素落在右边区间,此时将right更新为mid,再求mid,此时mid仍为指向刚才位置,即落在右边区间,此时再次更新right为mid,再次求mid... 从而死循环
上图中,当选择右边元素作为中间元素时,mid指向的元素落在右边区间,此时将right更新为mid,再求mid,此时mid仍为指向刚才位置,即落在右边区间,此时再次更新right为mid,再次求mid... 从而死循环
循环条件如何设置?
由于我们将right更新为mid,因此循环的条件应为left < right,若循环条件设置为left <= right,当left = right时,此时找到结果,而结果落在右边区间,此时会更新right的值,而right 更新为mid,即当前位置,从而死循环

分析完以上问题后,我们可以尝试编写查找右边区域最左边元素的代码:
//查找target第一次出现的位置(右边区间的左端点)
int left = 0,right = nums.length - 1,mid = left + (right - left)/2;
//循环条件应设置为left < right
//不能设置为left <= right,否则会死循环
while(left < right){//当mid所指向的元素落在左边区间时,更新leftif(nums[mid] < target){left = mid + 1;}else{//当mid所指向的元素落在右边区间时,此时更新right//由于右边区间的元素大于等于target,即结果在该区间内,// 因此不能将right更新为mid - 1,而应更新为midright = mid;}//更新mid,当有两个中间元素时,mid应指向其中左边的元素mid = left + (right - left) / 2;
}此时我们查找target最后一次出现的位置
与查找第一次出现位置的思路相同,我们首先将数组分为两个部分:

其中,左边区间内元素小于等于target,右边区间元素大于target
此时,要找的结果即为左边区间的右端点
 同样的,定义left指向0位置,right指向最后一个元素,mid指向中间位置
同样的,定义left指向0位置,right指向最后一个元素,mid指向中间位置
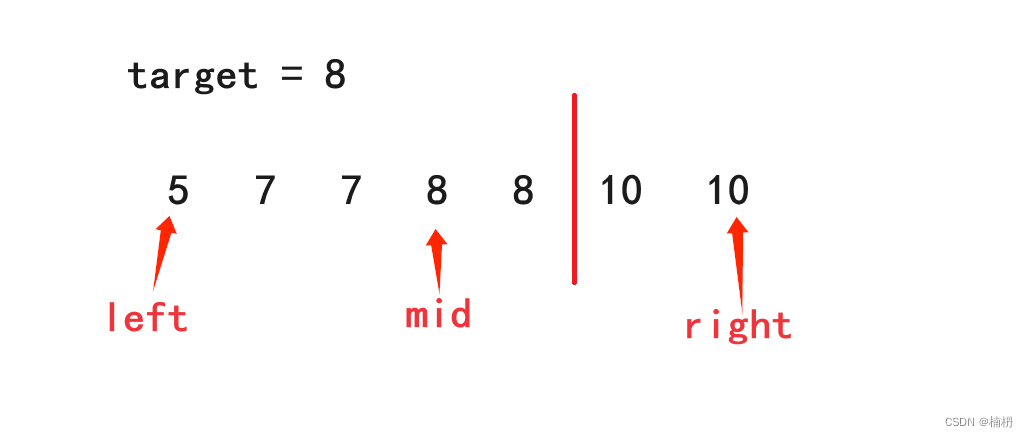
若mid所指向的元素落在左边区间,此时需要更新left的值,由于要找的结果落在此区间内,即mid所指向的位置可能就是最终结果,因此不能将left更新为mid + 1,而应更新为mid
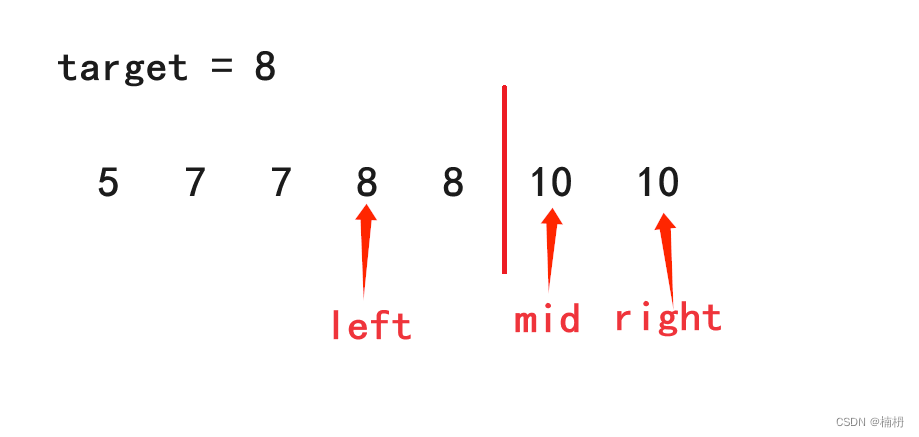
若mid所指向的元素落在右边区间,此时需要更新right的值,由于要找的结果不在右边区间,因此可将right的值更新为mid - 1
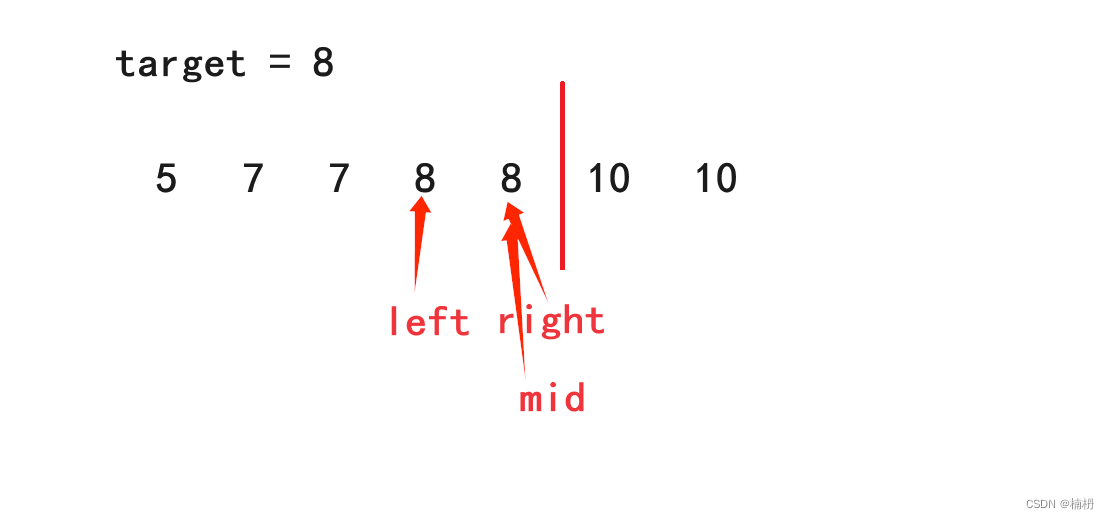
当left和right之间元素为偶数个时,此时中间元素有两个,应该选择哪一个作为中间元素?
由于我们查找的是左边区间内最右边的元素,因此,应该选择右边的元素作为中间元素
即 mid = left + (right - left + 1) / 2;
同样的,当选择左边元素作为中间元素时,也会造成死循环
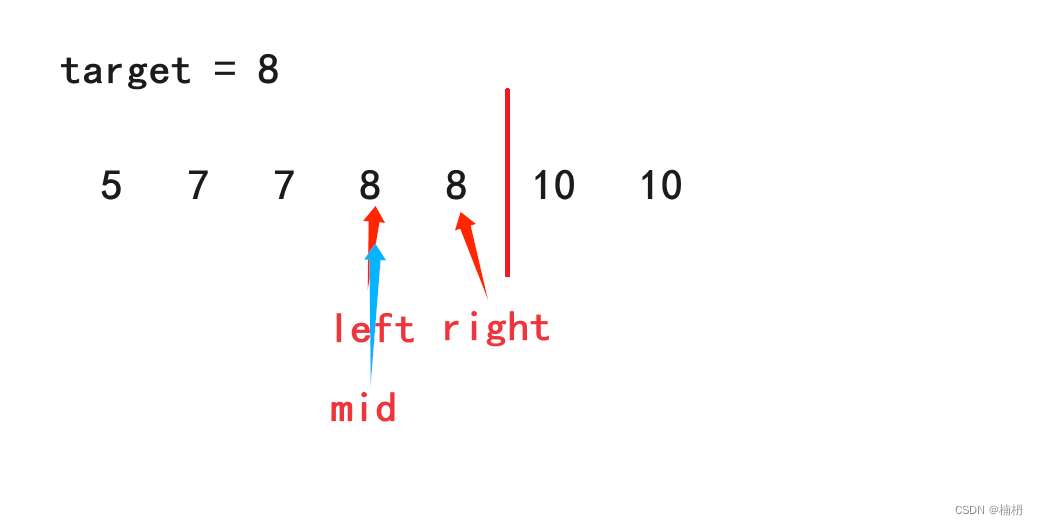
此时left的值一直更新为当前位置,造成死循环
循环条件的设置:
循环条件也同样应该设置为left < right,否则会死循环
此时我们尝试编写查找左边区间右端点代码:
//查找区间右端点
left = mid;
right = nums.length - 1;
mid = left + (right - left + 1)/2;
while(left < right){//当mid所指向的值落在右边区域时,更新右端点if(nums[mid] > target){right = mid - 1;}else{//当mid所指向的值落在左边区域时,更新左端点//由于左边区间的元素小于等于target,即结果在该区间内,//因此不能将left更新为mid + 1,而应更新为midleft = mid;}//更新mid的值,若有两个中间元素时,mid应指向其中右边的元素mid = left + (right - left + 1) / 2;
}完整代码:
class Solution {public int[] searchRange(int[] nums, int target) {int[] ret = {-1,-1};//若数组为空,直接返回retif(nums.length == 0){return ret;}//查找target第一次出现的位置(右边区间的左端点)int left = 0,right = nums.length - 1,mid = left + (right - left) / 2;//循环条件应设置为left < right//不能设置为left <= right,否则会死循环while(left < right){//当mid所指向的元素落在左边区间时,更新leftif(nums[mid] < target){left = mid + 1;}else{//当mid所指向的元素落在右边区间时,此时更新right//由于右边区间的元素大于等于target,即结果在该区间内,// 因此不能将right更新为mid - 1,而应更新为midright = mid;}//更新mid,当有两个中间元素时,mid应指向其中左边的元素mid = left + (right - left) / 2;}//此时left = right = mid,使用哪一个变量进行判断和更新都可以//若数组中无值为target的元素,直接返回retif(nums[left] == target){ret[0] = left;}else{return ret;}//查找区间右端点left = mid;right = nums.length - 1;mid = left + (right - left + 1)/2;while(left < right) {//当mid所指向的值落在右边区域时,更新右端点if (nums[mid] > target) {right = mid - 1;} else {//当mid所指向的值落在左边区域时,更新左端点//由于左边区间的元素小于等于target,即结果在该区间内,//因此不能将left更新为mid + 1,而应更新为midleft = mid;}//更新mid的值,若有两个中间元素时,mid应指向其中右边的元素mid = left + (right - left + 1) / 2;}ret[1] = left;return ret;}
}题目来自:
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
相关文章:

在排序数组中查找元素的第一个和最后一个位置(Java详解)
一、题目描述 给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 [-1, -1]。 你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。 示…...

k8s 安装firewalld导致的网络疑难问题处理
场景 ubuntu 操作系统,部署了k8s集群,n 台 机器,某些机器之间 telnet ip 10250不通。 ufw 是关闭的,然后抓包会看到如下错误 04:43:09.154362 IP 192.168.1.3.56608 > 192.168.1.183.8000: Flags [S], seq 3664350430, win 64240, options [mss 1460,sackOK,TS val 281…...
人工智能中的巨兽:图神经网络大模型的崛起
导言 图神经网络大模型的涌现标志着人工智能领域的一次革命。本文将深入研究这些庞大而强大的模型,探讨其背后的技术原理、关键应用以及引发的社会影响。 1. 技术原理 图神经网络大模型以其对图结构数据的卓越处理能力而著称。其技术原理包括: 图卷积神…...

【LeetCode刷题笔记(6-2)】【Python】【三数之和】【双指针】【中等】
文章目录 引言三数之和题目描述示例示例1示例2示例3 提示 解决方案3:【双指针】结束语 三数之和 引言 编写通过所有测试案例的代码并不简单,通常需要深思熟虑和理性分析。虽然这些代码能够通过所有的测试案例,但如果不了解代码背后的思考过程…...

02_Web开发基础之JavaScript
Web开发基础之JavaScript 学习目标和内容 1、能够描述Javascript的作用 2、能够使用分支结构if语句逻辑判断 3、能够使用其中一种循环语句 4、能够定义javaScript中的函数 5、能够定义javaScript中的对象 6、能够描述DOM的作用 7、能够通过DOM操作HTML标签元素及其属性 8、能够…...

如何控制Elasticsearch搜索的相关性?
控制相关性 纯粹处理结构化数据(例如日期、数字和 字符串枚举)很简单:他们只需要检查一个文档(或 行,在关系数据库中)与查询匹配。 虽然布尔值是/否匹配是全文搜索的重要组成部分,但它们 光靠自己是不够的。相反,我们还需要知道每个的相关性 document 是查询。全文搜索…...

基于urllib库的网页数据爬取
实验名称: 基于urllib库的网页数据爬取 实验目的及要求: 【实验目的】 通过本实验了解和掌握urllib库。 【实验要求】 1. 使用urllib库爬取百度搜索页面。 2. 使用urllib库获取百度搜索的关键字搜索结果(关键字任选)。 实验原理及…...
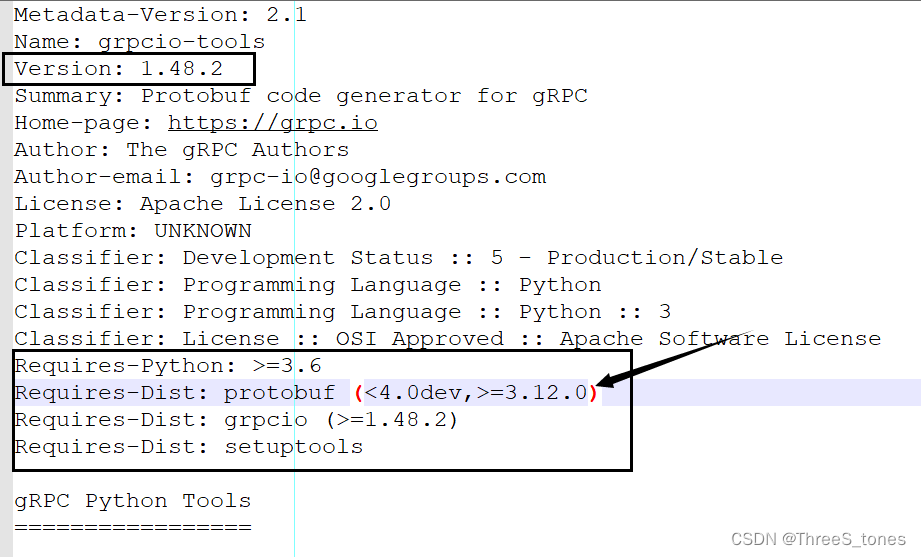
Python如何匹配库的版本
目录 1. 匹配库的版本 2. Python中pip,库,编译环境的问题回答总结 2.1 虚拟环境 2.2 pip,安装库,版本 1. 匹配库的版本 (别的库的版本冲突同理) 在搭建pyansys环境的时候,安装grpcio-tools…...
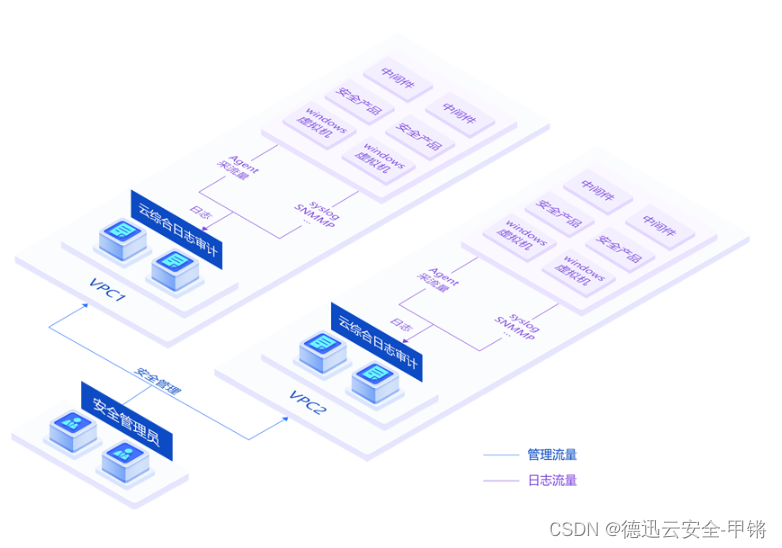
日志审计在网络安全中的重要性
日志审计是一种通过分析、识别和验证各种日志信息,以帮助企业了解其网络和系统的安全状态和活动的过程。这些日志信息可能来自各种来源,包括服务器、网络设备、应用程序、操作系统等。 日志审计的主要功能包括: 1.识别潜在的安全威胁&#…...

浅谈基于不信任的防御性编程
背景 在实际开发过程中,我们经常遇到这样的场景: 后端报错了,手忙脚乱一顿排查,发现是前端传的参数为空,或者格式不对;后端又报错了,传参没问题,根据日志流发现,是某“给…...
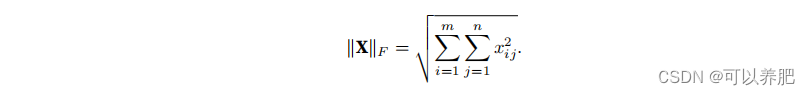
线性代数(一)
1.标量:标量由只有⼀个元素的张量表⽰。 x np.array(3.0) y np.array(2.0) x y, x * y, x / y, x ** y (array(5.), array(6.), array(1.5), array(9.))2.向量:向量可以被视为标量值组成的列表,列向量是向量的默认⽅向。 x np.arange(4…...

k8s-learning-why we need pod
应用场景 应用从虚拟机迁移到容器中 为什么虚拟机中的应用不能无缝迁移到容器中 虚拟机中应用:一组进程,被管理在systemd或者supervisord中 容器的本质:一个容器一个进程 所以将运行在虚拟机中的应用无缝迁移到容器中,与容器…...

【CASS精品教程】cass11提示“请不要在虚拟机中运行此程序”的解决办法
文章目录 一、问题提示二、解决办法一、问题提示 按照正常安装教程安装好南方测绘cass 11之后,打开的时候可能会有以下提示:请不要在虚拟机中运行此程序,如下图所示: 遇到问题,咱们就想办法解决问题,下面将自己尝试的方法及最终解决情况跟大家说一下,供参考。 二、解决…...

【算法Hot100系列】正则表达式匹配
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

html 基础学习笔记
Date:20231212 html标签 基础学习笔记 一、web和internet 1.1、Internet简介 Internet 是一个全球性的计算机互联网络,中文名称有"因特网"、“国际互联网”、“网际网”、"交互网络"等Internet提供的主要服务 Telnet、Email、www、BBS、FTP等…...

7-4 天梯赛的善良
天梯赛是个善良的比赛。善良的命题组希望将题目难度控制在一个范围内,使得每个参赛的学生都有能做出来的题目,并且最厉害的学生也要非常努力才有可能得到高分。 于是命题组首先将编程能力划分成了 106 个等级(太疯狂了,这是假的&…...

案例精选|聚铭综合日志分析系统助力长房集团“智慧房产”信息化建设
长沙房产(集团)有限公司(简称“长房集团”)始创于2004年3月,是一家由长沙市人民政府授权组建的国有独资企业。截至2021年底,企业总资产逾452亿元,总开发面积1300多万平方米,已开发项…...

HarmonyOS给应用添加消息通知
给您的应用添加通知 通知介绍 通知旨在让用户以合适的方式及时获得有用的新消息,帮助用户高效地处理任务。应用可以通过通知接口发送通知消息,用户可以通过通知栏查看通知内容,也可以点击通知来打开应用,通知主要有以下使用场景…...
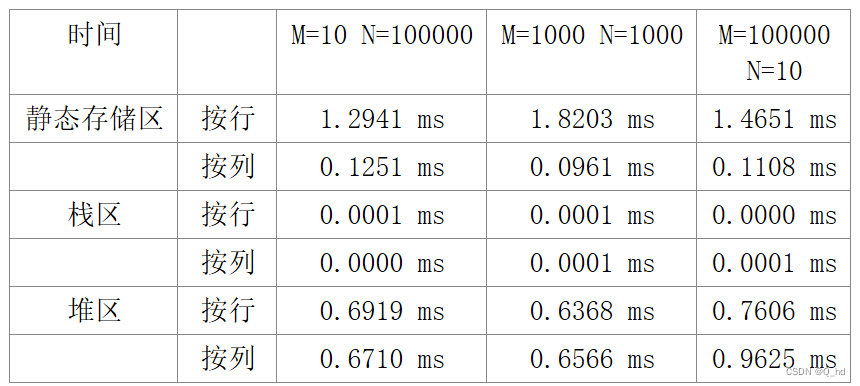
【C语言】cache和程序访问的局部性对程序性能的影响
文章目录 1.源程序比较其性能影响2.内存分配(1)静态存储区(static):(2)栈区(stack):(3)堆区(heap&…...
)
数字棱形(课程F)
输入1个整数N,输出N行的如下形状的数字棱形。 例如:N4时: ___1 __222 _33333 4444444 _33333 __222 ___1 (注:上面使用下划线’_’表示空格,以避免看不清造成误解) 输入格式 第一行1个正整数:N࿰…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
