算法通关第十九关-青铜挑战理解动态规划
大家好我是苏麟 , 今天聊聊动态规划 .
动态规划是最热门、最重要的算法思想之一,在面试中大量出现,而且题目整体都偏难一些对于大部人来说,最大的问题是不知道动态规划到底是怎么回事。很多人看教程等,都被里面的状态子问题、状态转移方程等等劝退了。
其实,所谓的状态就是一个数组,动态规划里的状态转移方程就是更新这个数组的方法。这一关,我们先理解动态规划到底怎么回事。
大纲
- 热身 : 斐波那契数列
- 路径连环问题
- 基本问题 : 统计路径总数
- 用二维数组优化递归
- 滚动数组 : 用一维数组代替二维数组
- 拓展问题 : 最小路径和
- 理解动态规划
热身 : 斐波那契数列
首先来感受一下什么是重复计算和记忆化搜索。
public class FibonacciTest {public static int count = 0;public static void main(String[] args) {fibonacci(20);System.out.println("count:" + count);}public static int fibonacci(int n) {System.out.println("斐波那契数列");count++;if (n == 0) {return 1;}if (n == 1 || n == 2)return n;else {return fibonacci(n - 1) + fibonacci(n - 2);}}
}
这个就是斐波那契数列,当n为20时,count是21891次。而当n=30 的时候结果是2692537,也就是接270万。如果纯粹只是算斐波那契数列,我们可以直接循环:
public static int count_2 = 0;public int fibonacci(int n) {if (n <= 2) {count_2++;return n;}int f1 = 1;int f2 = 2;int sum = 0;for (int i = 3; i <= n; i++) {count_2++;sum = f1 + f2;f1 = f2;f2 = sum;}return sum;}
n为30时也不过计算二十几个数的累加,但是为什么采用递归竟然高达270万呢?
因为里面存在大量的重复计算,数越大,重复越多。例如当n=10的时候,我们看下面的结构图就已经有很多重复计算了:
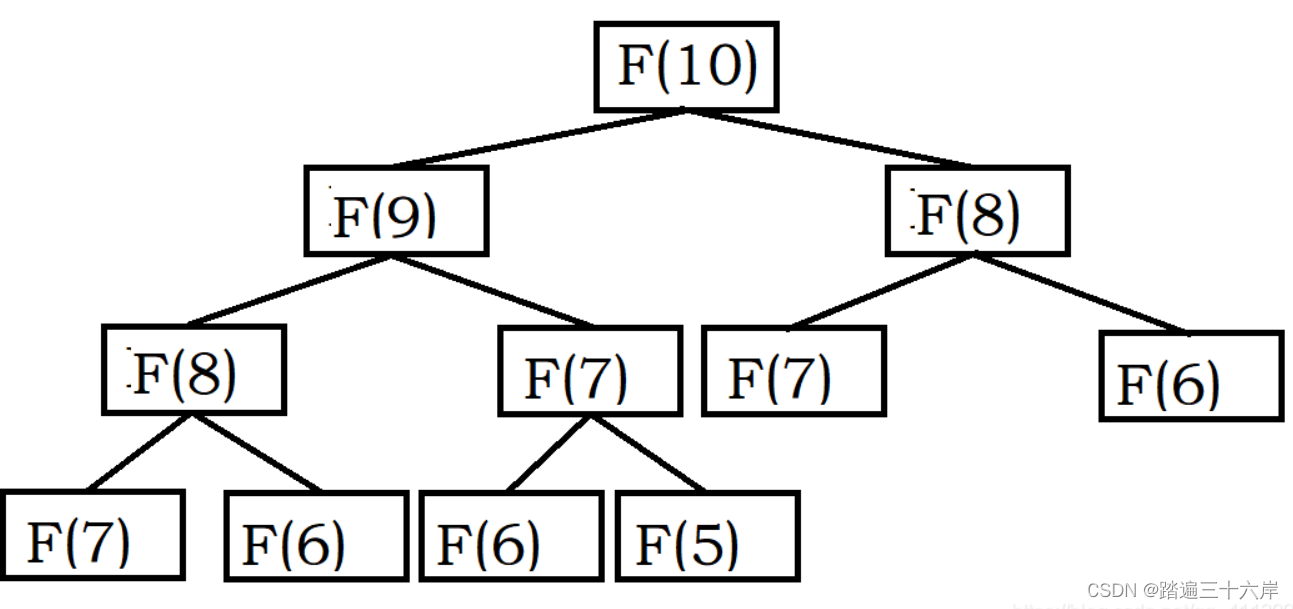
上面我们在计算f(10)时,可以看到f(9)、f(8)等等都需要计算,这就是重叠子问题。怎么对其优化一下呢?
可以看到这里主要的问题是很多数据都会频繁计算,如果将计算的结果保存到一个一维数组里。把 n 作为我们的数组下标,f(n)作为值,也就是 arr[n] = f(n)。执行的时候如果某人位置已经被计算出来了就更新对应位置的数组值,例如 f(4)算完了,就将其保存到arr[4]中,当后面再次要计算 f(4) 的时候,我们判断f(4)已经计算过,因此直接读取 f(4) 的值,不再递归计算。代码如下:
public static int[] arr = new int[50];public static int count_3 = 0;Arrays.fill(arr, -1);arr[0] = 1;int fibonacci ( int n){if (n == 2 || n == 1) {count_3++;arr[n] = n;return n;}if (arr[n] != -1) {count_3++;return arr[n];} else {count_3++;arr[n] = fibonacci(n - 1) + fibonacci(n - 2);return arr[n];}}
在上面代码里,在执行递归之前先查数组看是否被计算过,如果重复计算了,就直接读取,这就叫”记忆化搜索“,就这么简单。
路径连环问题
基本问题 : 统计路径总数
描述 :
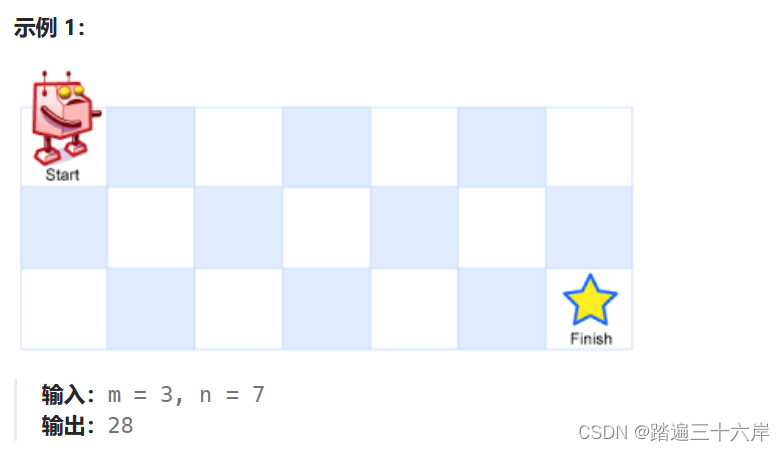
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
题目 :
LeetCode 62. 不同路径 :
不同路径
分析 :
我们先从一个3x2的情况来分析:
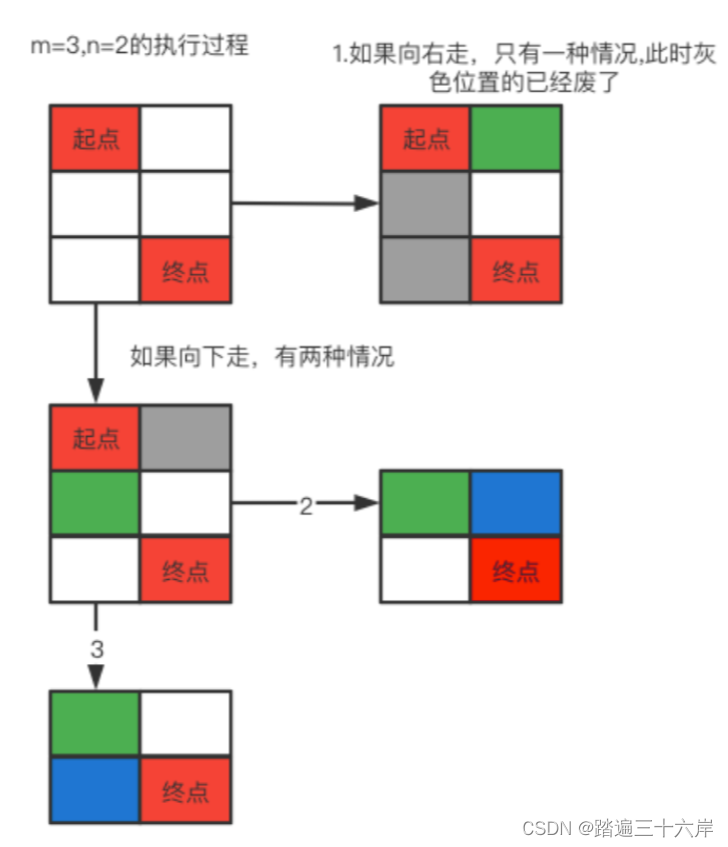
我们的目标是从起点到终点,因为只能向右或者向下,从图中可以可以看到:
1.如果向右走,也就是图1的情况,后面是一个3x1的矩阵,此时起点下面的两个灰色位置就不会再访问了,只能从绿色位置一直向下走,只有一种路径。
2.如果是向下走,我们可以看到原始起点右侧的就不能再访问了,而剩下的又是一个2X2的矩阵,也就是从图中绿色位置到红色位置,此时仍然可以选择向右或者向下,一共有两种路径。
所以上面的情况加起来就是一共有3种。
我们再看一下3X3的 :
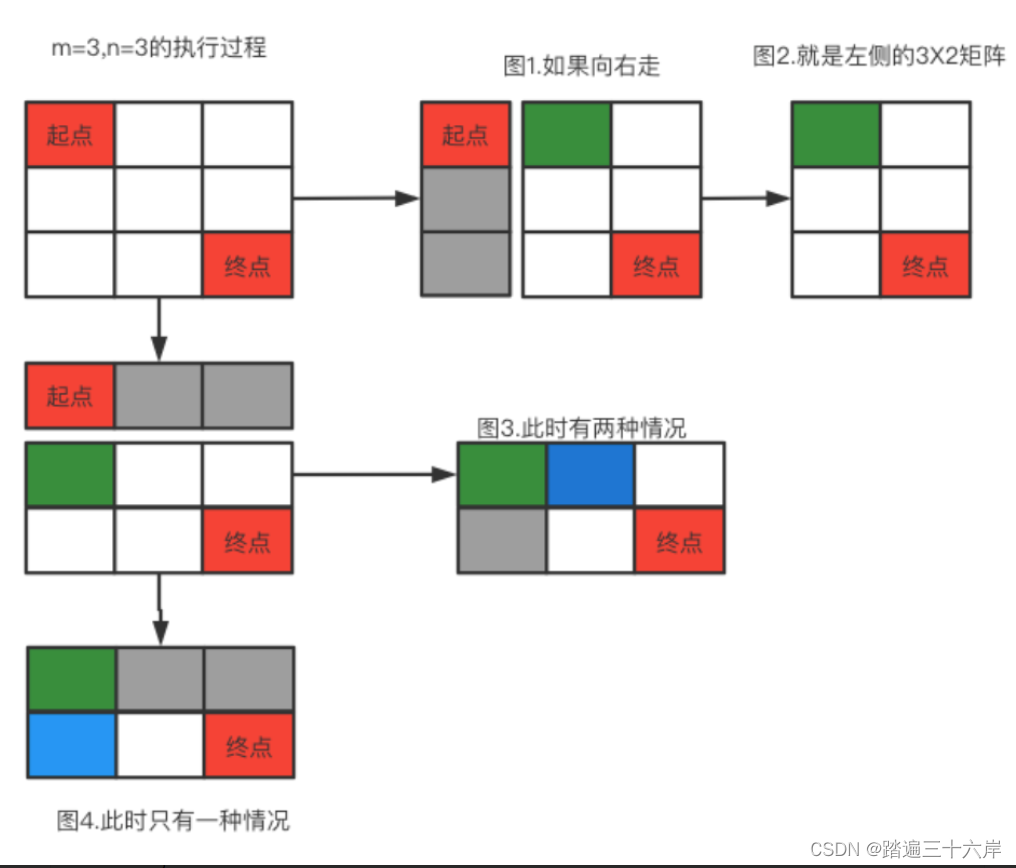
可以看到,一个3X3的矩阵下一步就变成了一个3X2或者2X3的矩阵,而总路径数,也是是两者各自的路径之和。
因此,对于一个mxn的矩阵,求路径的方法search(m,n)就是:search(m-1,n)+search(m,n-1);
递归的含义就是处理方法不变,但是问题的规模减少了
解析 :
注意 :递归的方式会超出时间限制
class Solution {public int uniquePaths(int m, int n) {return dp(m,n);}public int dp(int m,int n){if(n == 1 || m == 1){return 1;}return dp(m - 1,n) + dp(m,n - 1);}
}
用二维数组优化递归
我们来优化递归的问题,研究如何结合二维数组来实现记忆化搜索.
从上面这个树也可以看到在递归的过程中存在重复计算的情况,例如1,1出现了两次,如果是一个NXN的空间,那 1.0 和 0,1 的后续计算也是一样的。从二维数组的角度,例如在位置(1,1)处,不管从(0,1)还是(1,0)到来,接下来都会产生2种走法,因此不必每次都重新遍历才得到结果。
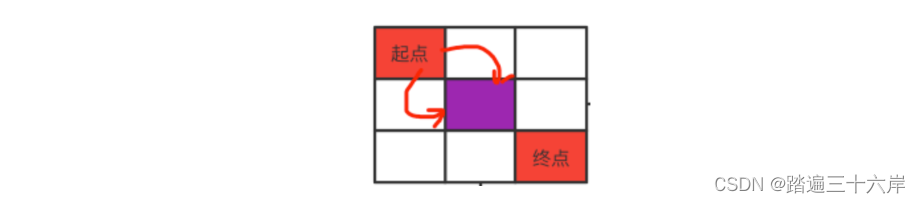
为此,我们可以采取一个二维数组来进行记忆化搜索,算好的就记录在数组中,也就是这样子:
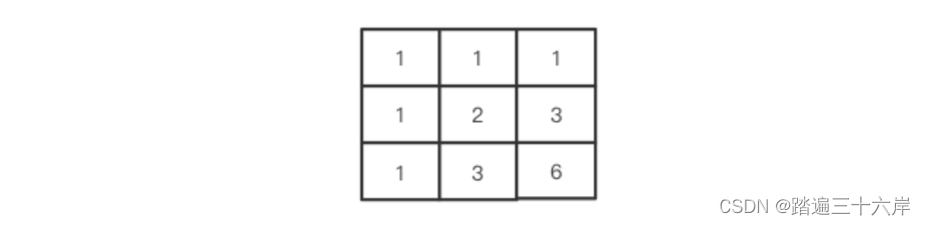
每个格子的数字表示从起点开始到达当前位置有几种方式,这样我们计算总路径的时候可以先查一下二维数组有没有记录,如果有记录就直接读,没有再计算,这样就可以大量避免重复计算,这就是记忆化搜索
根据上面的分析,我们可以得到两个规律:
1.第一行和第一列都是1。
2.其他格子的值是其左侧和上方格子之和。对于其他m,n的格子,该结论一样适用的,例如:

比如图中的4,是有上面的1和左侧的3计算而来,15是上侧的5和左侧的10计算而来。如果用公式表示就是:
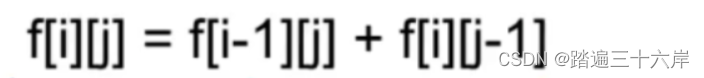
解析 :
class Solution {public int uniquePaths(int m, int n) {int[][] arr = new int[m][n];arr[0][0] = 1;for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){if(i > 0 && j > 0){arr[i][j] = arr[i - 1][j] + arr[i][j - 1];}else if(i > 0){arr[i][j] = arr[i - 1][j];}else if(j > 0){arr[i][j] = arr[i][j - 1];}}}return arr[m - 1][n - 1];}
}
滚动数组 : 用一维数组代替二维数组
我们通过滚动数组来优化此问题。上面的缓存空间使用的是二维数组,这个占空间太大了,能否
进一步优化呢?
我们再看一下上面的计算过程:
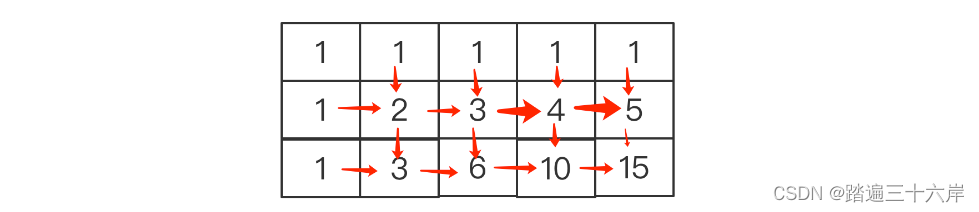
在上图中除了第一行和第一列都是1外,每个位置都是其左侧和上访的格子之和,那我可以用一个大小为n的一维数组解决来:
第一步,遍历数组,将一维数组所有元素赋值为1

第二步,再次从头遍历数组,除了第一个,后面每个位置是其原始值和前一个位置之和,也就是这样:

第三步:重复第二步:除了第一个,后面每个位置仍然是其原始值和前一个位置之和,也就是这样:

- 继续循环,题目给的m是几就循环几次,要得到结果,输出最后一个位置的15就可以了.
上面这几个一维数组拼接起来,是不是发现和上面的二维数组完全一样的? 而这里我们使用了一个一维数组就解决了,这种反复更新数组的策略就是滚动数组.计算公式是:

解析 :
class Solution {public int uniquePaths(int m, int n) {int[] arr = new int[n];Arrays.fill(arr,1);for(int i = 1;i < m;i++){for(int j = 1;j < n;j++){arr[j] = arr[j - 1] + arr[j];}}return arr[n - 1];}
}
拓展问题 : 最小路径和
描述 :
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
题目 :
LeetCode 64. 最小路径和 :
最小路径和 :
分析 :
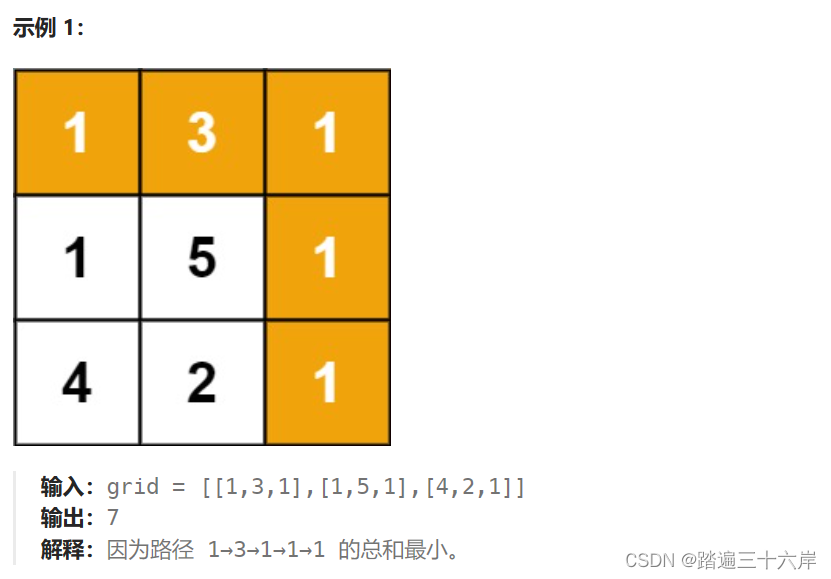
这道题是在上面题目的基础上,增加了路径成本概念。由于题目限定了我们只能[往下]或者[往右]移动,因此我们按照当前位置可由哪些位置转移过来 进行分析:
- 当前位置只能通过[往下] 移动而来,即有f[i][j] = f[i-1][j] + grid[i][j]
- 当前位置只能通过[往右]移动而来,即有 f[i][j] = f[i][j-1] + grid[i][j]
- 当前位置既能通过[往下]也能[往右] 移动,即有f[i][j] = min(f[i][j - 1],f[i - 1][j]) + grid[i][j]
二维数组的更新过程,我们可以图示一下:
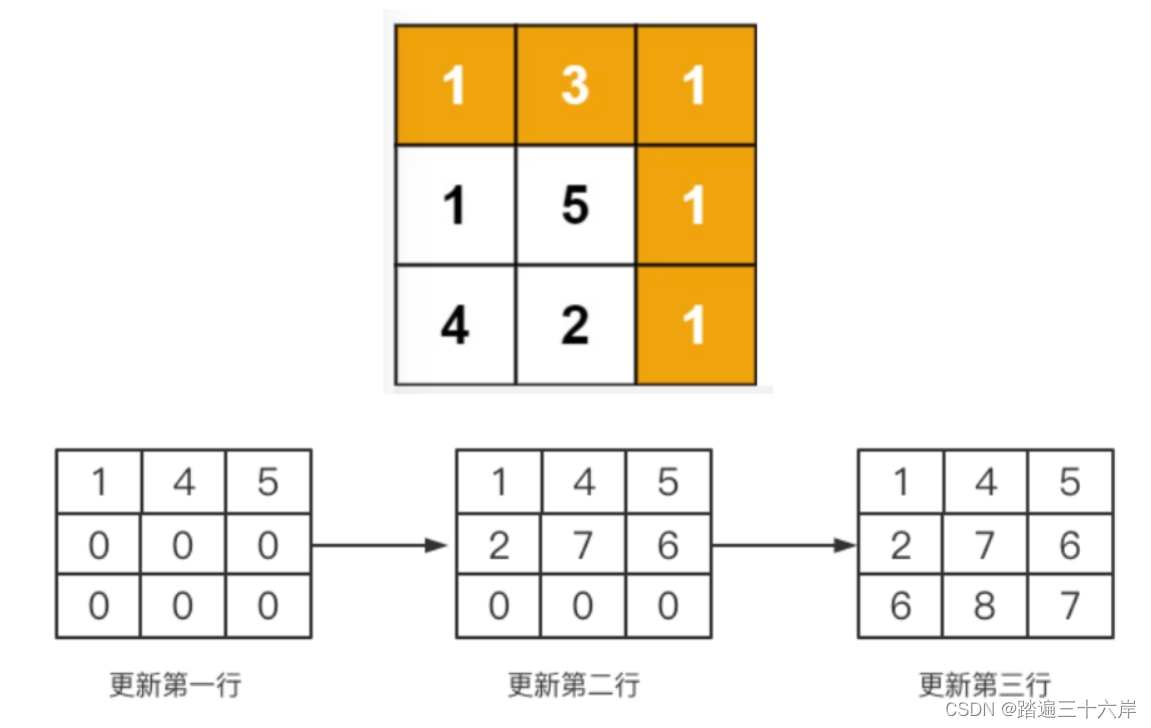
我们现在可以引入另外一个概念状态: 所谓状态就是下面表格更新到最后的二维数组,而通过前面格子计算后面格子的公式就叫状态转移方程。如果用数学表达就是:
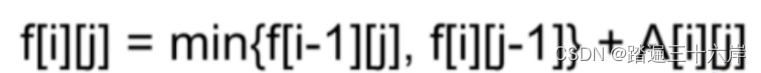
所谓的确定状态转移方程就是要找递推关系,通常我们会从分析首尾两端的变化规律来入手。
解析 :
class Solution {public int minPathSum(int[][] grid) {int m = grid.length;int n = grid[0].length;int[][] arr = new int[m][n];for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){if(i == 0 && j == 0){arr[i][j] = grid[i];}else{int top = i - 1 >= 0 ? arr[i - 1][j] + grid[i][j] : Integer.MAX_VALUE; int left = j - 1 >= 0 ? arr[i][j - 1] + grid[i][j] :
Integer.MAX_VALUE;arr[i][j] = Math.min(top,left);}}}return arr[m - 1][n - 1];}
}
理解动态规划
DP能解决哪类问题? 直观上,DP一般是让找最值的,例如最长公共子序列等等,但是最关键的是DP问题的子问题不是相互独立的,如果递归分解直接分解会导致重复计算指数级增长。而DP最大的价值是为了消除冗余,加速计算 .
这期就到这里下期见 !
相关文章:
算法通关第十九关-青铜挑战理解动态规划
大家好我是苏麟 , 今天聊聊动态规划 . 动态规划是最热门、最重要的算法思想之一,在面试中大量出现,而且题目整体都偏难一些对于大部人来说,最大的问题是不知道动态规划到底是怎么回事。很多人看教程等,都被里面的状态子问题、状态…...
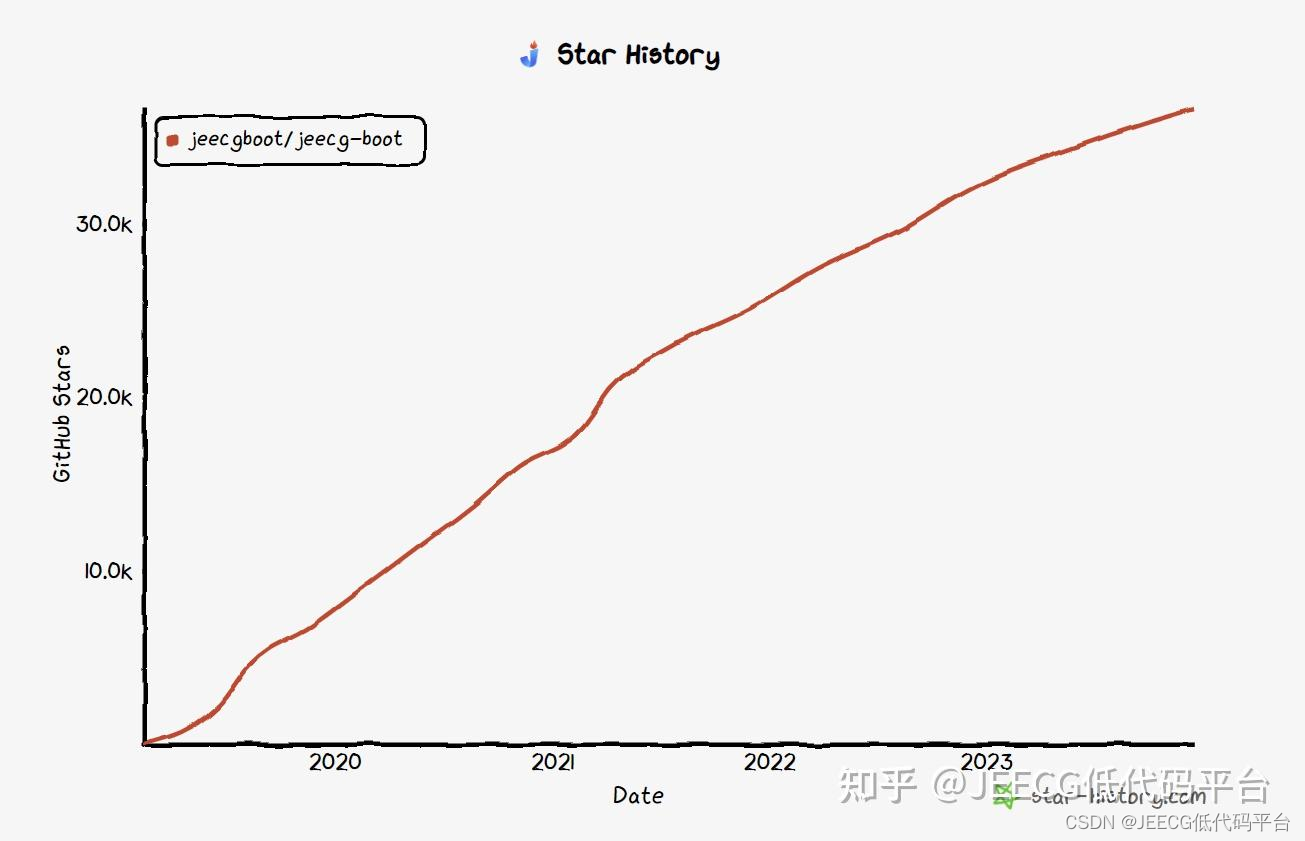
2023 GitHub年度排行榜,JEECG上榜第三名,势头依然很猛~
2023 GitHub年度排行榜TOP10,JeecgBoot上榜第三名,势头依然很猛~...
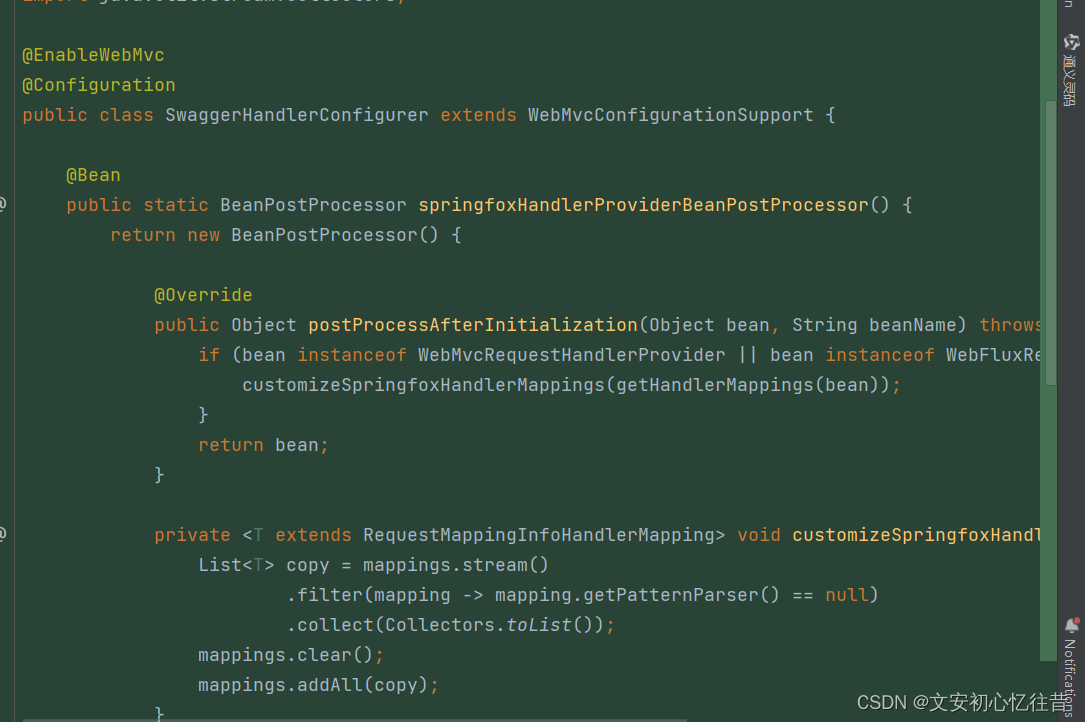
由@EnableWebMvc注解引发的Jackson解析异常
同事合了代码到开发分支,并没有涉及到改动的类却报错。错误信息如下: Servlet.service() for servlet [dispatcherServlet] in context with path [] threw exception [Request processing failed; nested exception is org.springframework.http.conv…...

ce从初阶到大牛--函数
1、显示/etc/passwd文件中以bash结尾的行; grep "bash$" /etc/passwd2、找出/etc/passwd文件中的三位或四位数; grep -E \b[0-9]{3,4}\b /etc/passwd3、找出/etc/grub2.cfg文件中,以至少一个空白字符开头,后面又跟了非…...

Java学习异常类
1 定义 异常就是指程序运行时可能出现的一些错误,例如数组越界、除零等。 我们也可以把自己觉得不合理的结果定义为“异常” 2 异常与错误 3 Java中的异常处理 catch语句:对异常的处理语句放在 catch部分,可以包含多个catch语句,…...
Python 全栈体系【四阶】(六)
第四章 机器学习 五、线性模型 1. 概述 线性模型是自然界最简单的模型之一,它描述了一个(或多个)自变量对另一个因变量的影响是呈简单的比例、线性关系。例如: 住房每平米单价为 1 万元,100 平米住房价格为 100 万…...
函数中学习函数的设计思想)
从memcpy()函数中学习函数的设计思想
memcpy()函数:可以理解为内存拷贝。 他的函数定义如下的 my_memcpy()函数相同。 下面这个函数是我的模拟实现,现在让我们一起来学习一下这个函数的设计思想: void * my_memcpy(void * des, const void* src, size_t size) {void * p des;…...
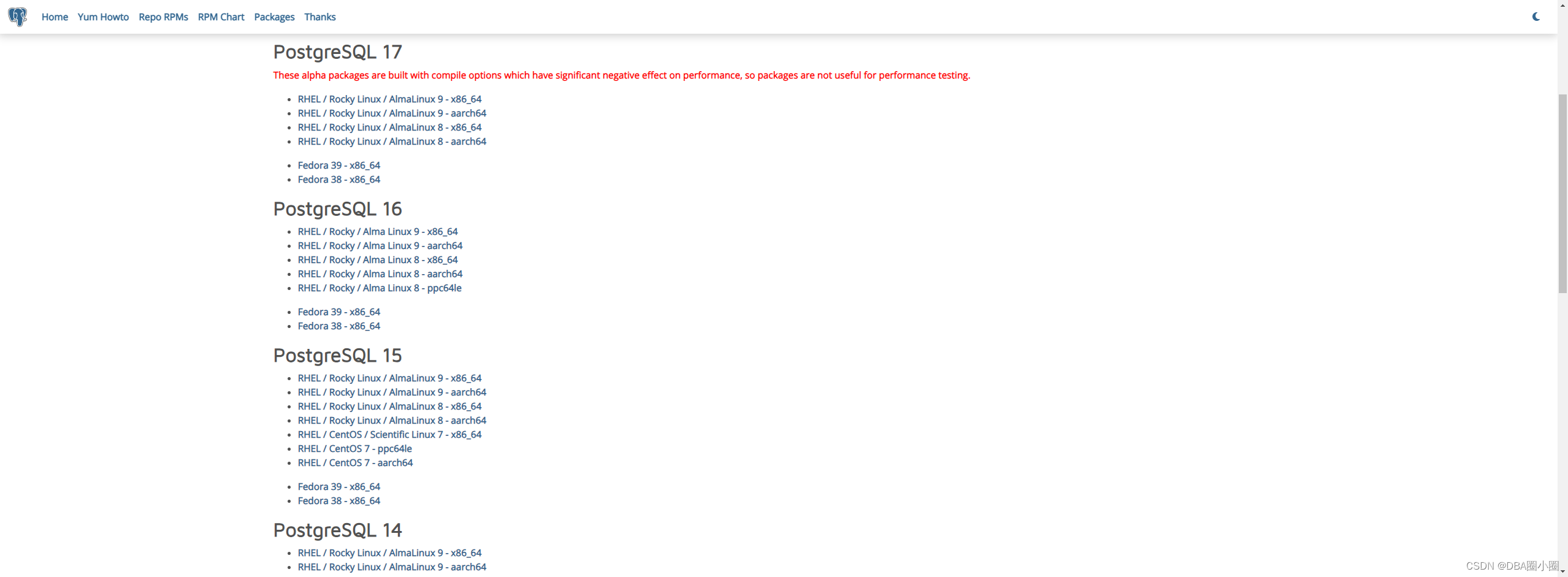
【PostgreSQL】从零开始:(二)PostgreSQL下载与安装
【PostgreSQL】从零开始:(二)PostgreSQL下载与安装 Winodws环境下载与安装PostgreSQL下载PostgreSQL安装PostgreSQL1.登录数据库2.查看下我们已有的数据库 Liunx环境下载与安装PostgreSQL使用YUM下载安装PostgreSQL1.下载PostgreSQL安装包2.安装PostgreS…...

PHP的垃圾回收机制是怎样的?
PHP 使用自动垃圾回收机制来管理内存。PHP 的垃圾回收主要依赖于引用计数和周期性垃圾回收两种策略。 引用计数: PHP 使用引用计数来跟踪变量的引用次数。每当一个变量被引用,其引用计数就增加;每当一个引用被释放,计数就减少。当…...

【数据结构】八大排序之希尔排序算法
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 一.优化直接插入排序算法 我们在之前对直接插入排序算法的优化部分通过对直接插入排序的分析可以得到一个结论,即: 进行直接插入排序的数组,如果越接近局部有序,则后续进行直…...

NestJS使用gRPC实现微服务通信
代码仓库地址:https://github.com/zeng-jc/rpc-grpc-practice 1.1 基本概念 gRPC 基于 Protocol Buffers(protobuf)作为接口定义语言(IDL),意味着你可以使用 protobuf 来定义你的服务接口,gRP…...

Android手机使用Termux终端模拟器
Termux 是 Android 平台上的一个终端模拟器,可以在 Android 手机上模拟 Linux 环境。它提供命令行界面,并且提供了功能健全的包管理工具(pkg)。另外就是 Termux 不需要 root 权限,安装后默认产生一个用户,可…...
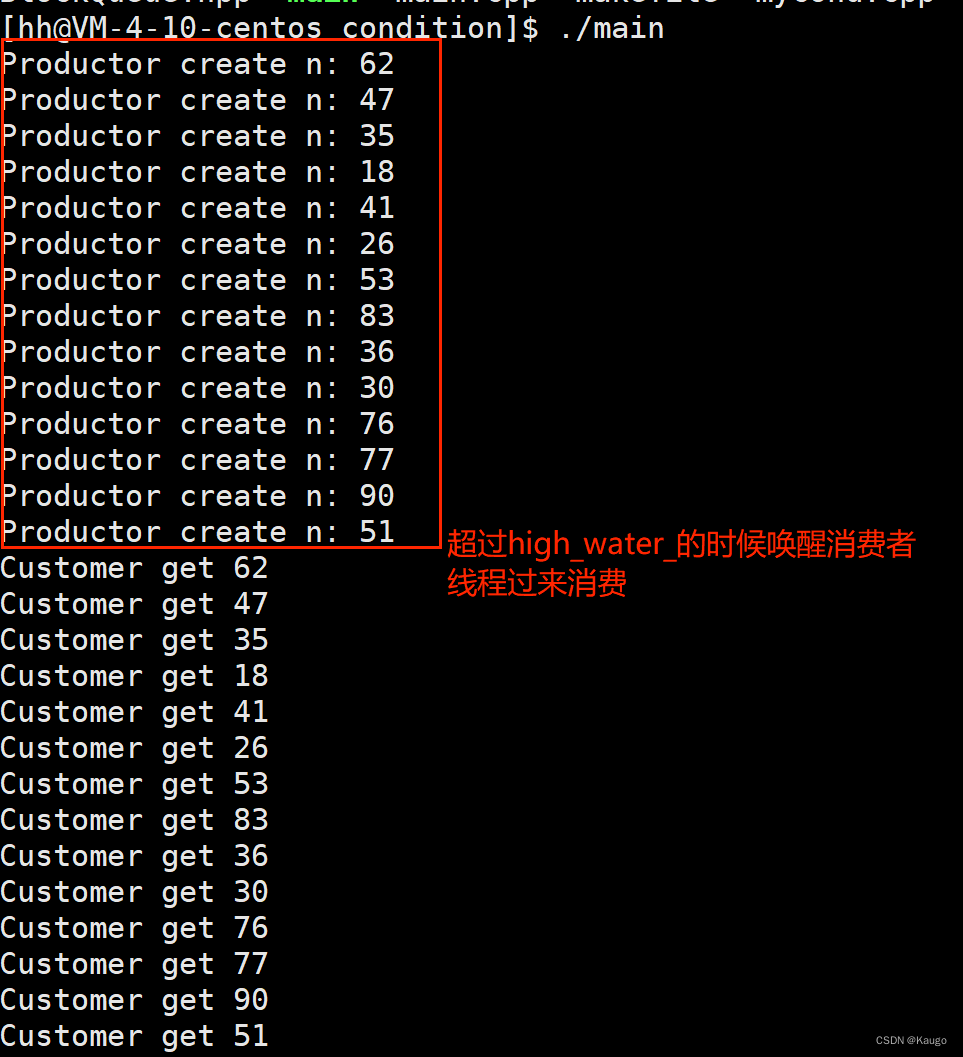
【Linux】cp问题,生产者消费者问题代码实现
文章目录 前言一、 BlockQueue.hpp(阻塞队列)二、main.cpp 前言 生产者消费者模式就是通过一个容器来解决生产者和消费者的强耦合问题。生产者和消费者彼此之间不直接通讯,而通过阻塞队列来进行通讯,所以生产者生产完数据之后不用…...

C++1114新标准——统一初始化(Uniform Initialization)、Initializer_list(初始化列表)、explicit
系列文章目录 C11&14新标准——Variadic templates(数量不定的模板参数) C11&14新标准——Uniform Initialization(统一初始化)、Initializer_list(初始化列表)、explicit 文章目录 系列文章目录1…...
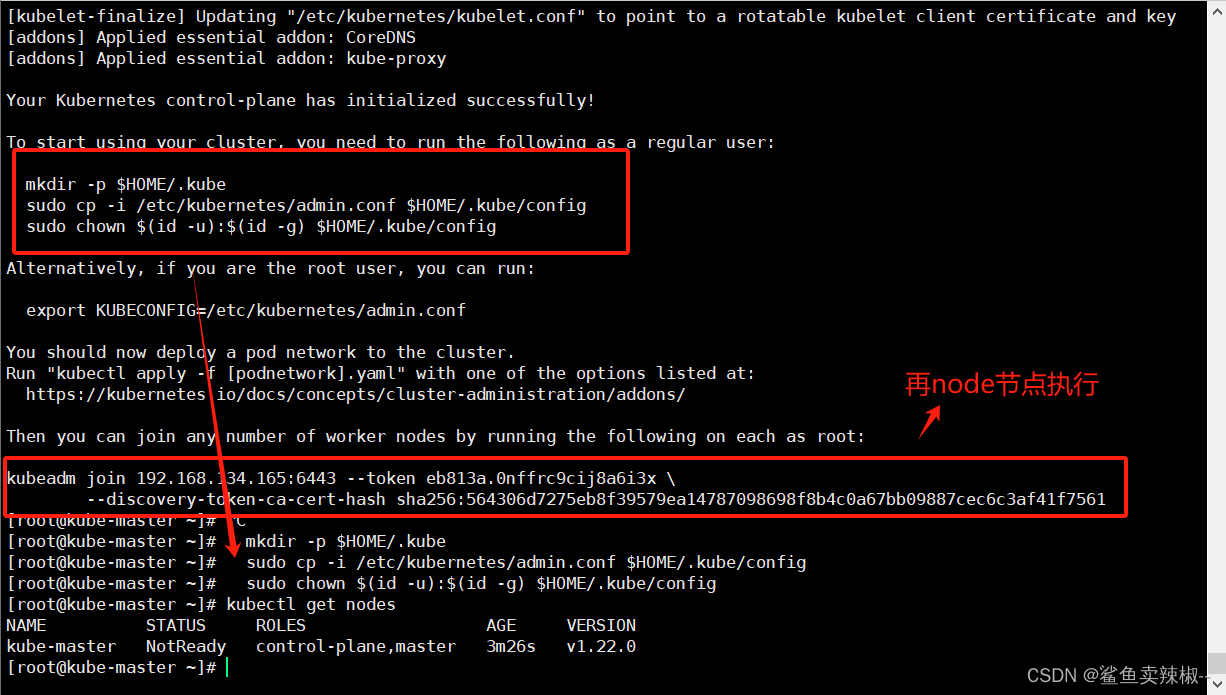
Kubeadm 方式部署K8s集群
环境 主节点CPU核数必须是 ≥2核且内存要求必须≥2G,否则k8s无法启动 主机名地址角色配置kube-master192.168.134.165主节点2核4Gkube-node1192..168.134.166 工作节点2核4Gkube-node2192.168.134.163工作节点2核4G 1.获取镜像 谷歌镜像[由于国内网络原因…...

力扣376周赛
力扣第376场周赛 找出缺失和重复的数字 map模拟 class Solution { public:vector<int> findMissingAndRepeatedValues(vector<vector<int>>& grid) {int n grid.size() , m grid[0].size();map<int,int>mi;for(int i 0 ; i < n ; i ){for…...

SU渲染受到电脑性能影响大吗?如何提高渲染速度
一般3d设计师们在进行设计工作前都需要提供一台高配电脑,那么你这知道su渲染对电脑要求高吗?电脑带不动su怎么解决?su对电脑什么配件要求高?今天这篇文章就详细为大家带来电脑硬件对su建模渲染的影响,以及su渲染慢怎么…...
Docker - Android源码编译与烧写
创建源代码 并挂载到win目录 docker run -v /mnt/f/android8.0:/data/android8.0 -it --name android8.0 49a981f2b85f /bin/bash 使用 docker update 命令动态调整内存限制: 重新运行一个容器 docker run -m 512m my_container 修改运行中容器 显示运行中容器 d…...
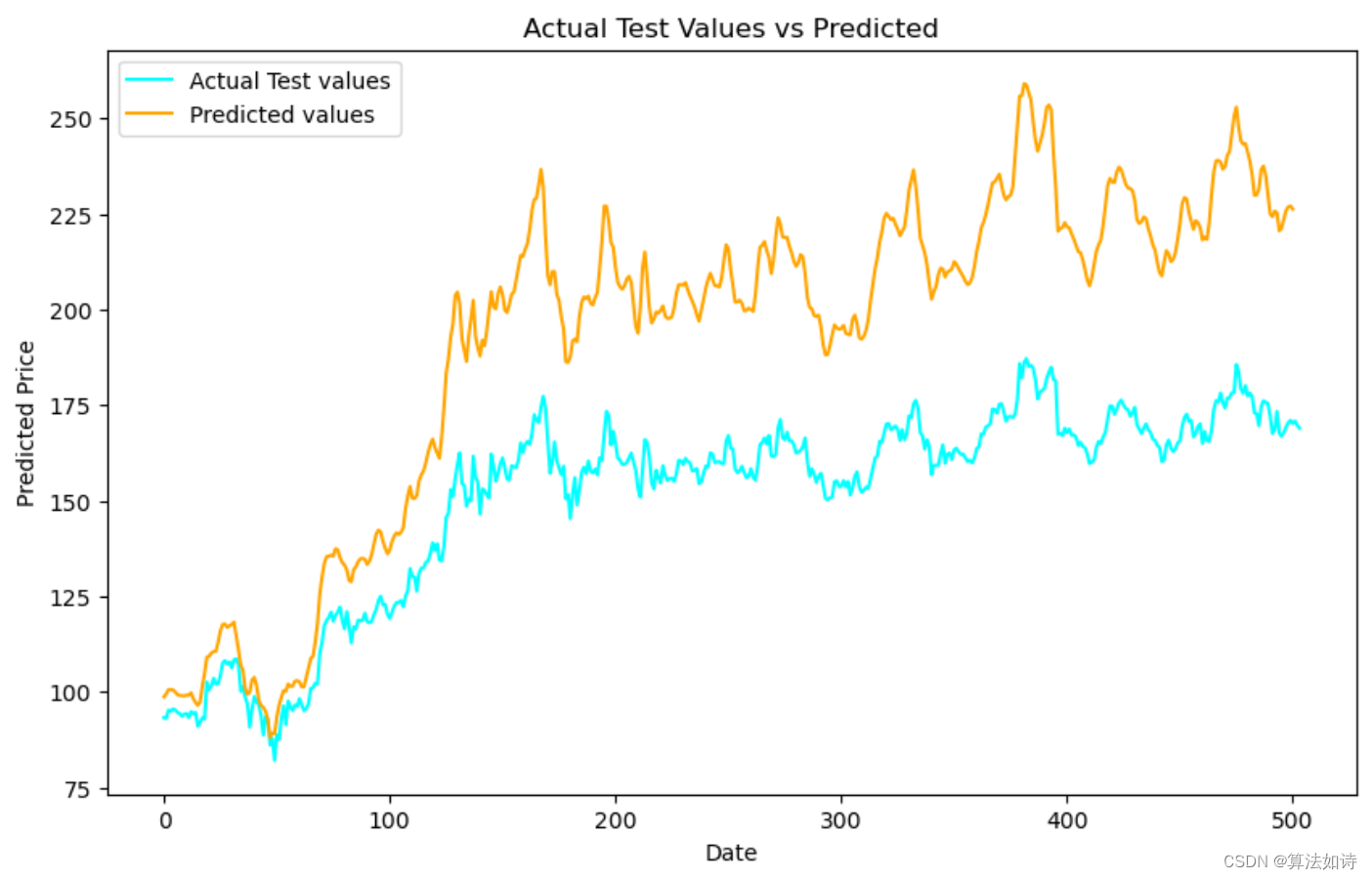
股票价格预测 | Python实现基于ARIMA和LSTM的股票预测模型(含XGBoost特征重要性衡量)
文章目录 效果一览文章概述模型描述源码设计效果一览 文章概述 Python实现基于ARIMA和LSTM的股票预测模型(Stock-Prediction) Data ExtractionFormatting data for time seriesFeature engineering(Feature Importance using X...
Base64
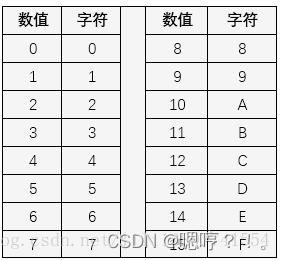
1. Base64是什么? Base64(基底64)是一种基于64个可打印字符来表示二进制数据的表示方法。每6个比特为一个单元,对应某个可打印字符。3个字节相当于24个比特,对应于4个Base64单元,即3个字节可由4个可打印字…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
