LeetCode刷题--- 子集
个人主页:元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客
个人专栏
- 力扣递归算法题【 http://t.csdnimg.cn/yUl2I 】
- 【C++】 【 http://t.csdnimg.cn/6AbpV 】
- 数据结构与算法【 http://t.csdnimg.cn/hKh2l 】
前言:这个专栏主要讲述递归递归、搜索与回溯算法,所以下面题目主要也是这些算法做的
我讲述题目会把讲解部分分为3个部分:
1、题目解析
2、算法原理思路讲解
3、代码实现
子集
题目链接:子集
题目
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0] 输出:[[],[0]]
提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums中的所有元素 互不相同
解法
题目解析
题目意思很简单,给我们一个数组,返回其 所有可能的子集
示例 1:
输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
算法原理思路讲解
解法一

决策树就是我们后面设计函数的思路
二、设计代码
(1)全局变量
vector<vector<int>> ret;vector<int> path;(2)设计递归函数
void dfs(vector<int>& nums, int pos);- 递归结束条件:如果当前需要处理的元素下标越界,则记录当前状态并直接返回;
- 在递归过程中,对于每个元素,我们有两种选择:
- 不选择当前元素,直接递归到下⼀个元素;
- 选择当前元素,将其添加到数组末尾后递归到下⼀个元素,然后在递归结束时撤回添加操作;
- 所有符合条件的状态都被记录下来,返回即可。
解法二
一、画出决策树
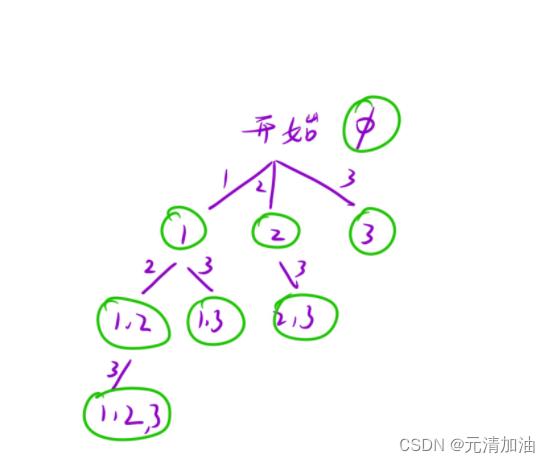
决策树就是我们后面设计函数的思路
二、设计代码
(1)全局变量
vector<vector<int>> ret;vector<int> path;1.递归函数头设计
void dfs(vector<int>& nums, int pos);参数:nums 数组,pos 在数组中的位置
- 在递归过程中,对于每个元素,我们只能向后选择:
- 选择当前元素,将其添加到数组末尾后递归到下⼀个元素,然后在递归结束时撤回添加操作(也即是回溯)
- 所有符合条件的状态都被记录下来,返回即可。
代码实现
解法一
时间复杂度:O(n×2^n)。一共 2^n个状态,每种状态需要 O(n) 的时间来构造子集。
空间复杂度:O(n)。临时数组 t 的空间代价是 O(n),递归时栈空间的代价为 O(n)。
class Solution
{vector<vector<int>> ret;vector<int> path;
public:void dfs(vector<int>& nums, int pos){if(pos == nums.size()){ret.push_back(path);return;}// 选path.push_back(nums[pos]);dfs(nums, pos + 1);path.pop_back(); // 恢复现场// 不选dfs(nums, pos + 1);}vector<vector<int>> subsets(vector<int>& nums) {dfs(nums, 0);return ret;}};解法二
class Solution
{vector<vector<int>> ret;vector<int> path;public:vector<vector<int>> subsets(vector<int>& nums) {dfs(nums, 0);return ret;}void dfs(vector<int>& nums, int pos){ret.push_back(path);for(int i = pos; i < nums.size(); i++){path.push_back(nums[i]);dfs(nums, i + 1);path.pop_back(); // 恢复现场}}
};相关文章:

LeetCode刷题--- 子集
个人主页:元清加油_【C】,【C语言】,【数据结构与算法】-CSDN博客 个人专栏 力扣递归算法题【 http://t.csdnimg.cn/yUl2I 】【C】 【 http://t.csdnimg.cn/6AbpV 】数据结构与算法【 http://t.csdnimg.cn/hKh2l 】 前言:这个专栏主要讲…...
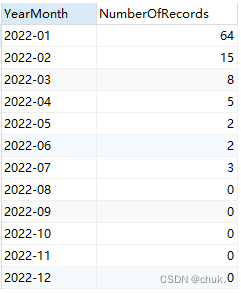
【SQL】根据年份,查询每个月的数据量
根据年份,查询每个月的数据量 一种 WITH Months AS (SELECT 1 AS Month UNION ALL SELECT 2 UNION ALL SELECT 3 UNION ALL SELECT 4 UNION ALL SELECT 5 UNION ALL SELECT 6 UNION ALL SELECT 7 UNION ALL SELECT 8 UNION ALL SELECT 9 UNION ALL SELECT 10 UNION…...

基于CTF探讨Web漏洞的利用与防范
写在前面 Copyright © [2023] [Myon⁶]. All rights reserved. 基于自己之前在CTF中Web方向的学习,总结出与Web相关的漏洞利用方法,主要包括:密码爆破、文件上传、SQL注入、PHP伪协议、反序列化漏洞、命令执行漏洞、文件包含漏洞、Vim…...
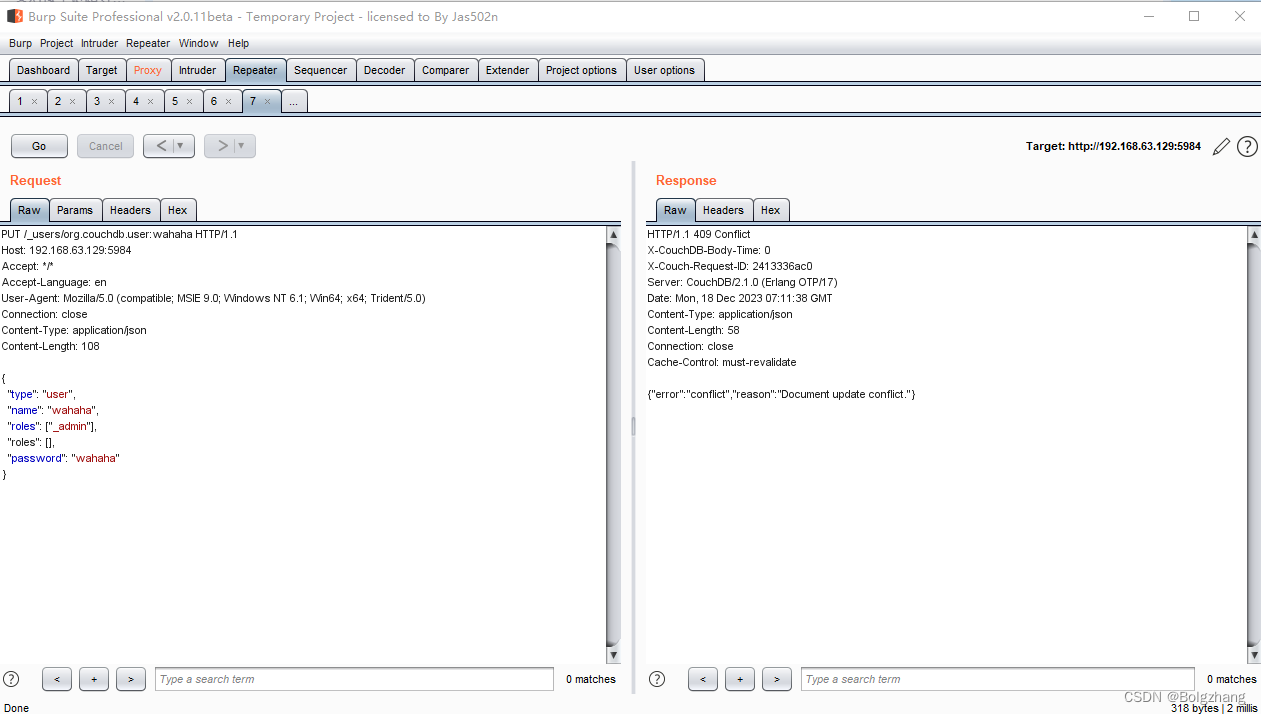
Apache CouchDB 垂直权限绕过漏洞 CVE-2017-12635 已亲自复现
Apache CouchDB 垂直权限绕过漏洞 CVE-2017-12635 已亲自复现 漏洞名称影响版本影响版本 漏洞复现环境搭建漏洞利用 总结 漏洞名称 影响版本 Apache CouchDB是一个开源的NoSQL数据库,专注于易用性和成为“完全拥抱web的数据库”。它是一个使用JSON作为数据存储格式…...
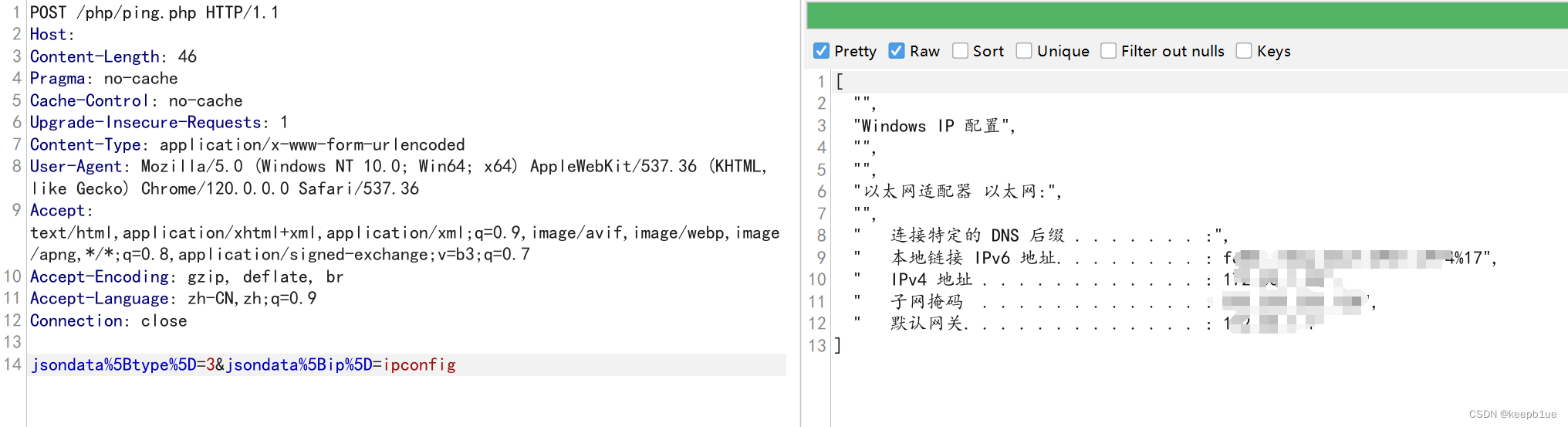
海康威视IP网络对讲广播系统命令执行漏洞(CVE-2023-6895)
漏洞介绍 海康威视IP网络对讲广播系统采用领先的IPAudio™技术,将音频信号以数据包形式在局域网和广域网上进行传送,是一套纯数字传输系统。 Hikvision Intercom Broadcasting System 3.0.3_20201113_RELEASE(HIK)版本存在操作系统命令注入漏洞,该漏洞源于文件/ph…...

IDE:DevEco Studio
简介 DevEco Studio是华为为开发者提供的一款集成开发环境(IDE),主要用于开发鸿蒙操作系统(HarmonyOS)的应用程序。作为一款全场景分布式开发工具,DevEco Studio支持多端开发、调试和模拟,为开…...
【QT】C++/Qt使用Qt自带工具windeployqt打包
基本操作 运行项目debug或者release 将运行后的可执行文件单独放到一个文件夹中 根据项目使用的kits来选择Qt的打包工具 打开工具后移动到exe文件夹下执行windeployqt xxx.exe 预览图 问题 打包后再其他电脑上运行出现下图错误 将自己电脑的这个文件拷到可执行文件夹中既…...

Ubuntu系统的基础操作和使用
文章目录 系统安装系统界面文件系统包管理命令行常见问题 Ubuntu是一个基于Debian的Linux发行版,以桌面应用为主。它是自由软件,意味着你可以自由地使用、复制、研究、修改和改进这个软件。下面我们将详细介绍Ubuntu系统的基础操作和使用。 系统安装 U…...
harmonyOS 自定义组件基础演示讲解
上文 HarmonyOS组件属性控制 链式编程格式推荐我们讲了一些系统组件 可以传入一些事件和参数 来达到一些不同的效果 其实 我们还可以用自己写的组件 那么 组件这么写? 其实 我们的 page 内部结果 就是一个组件 harmonyOS的概念 万物皆组件 那么 我们就可以在他下面…...

我的创作纪念日——成为创作者第1024天
机缘 一、前言 早上收到CSDN的推送信息,今天是我成为创作者的第1024天,回想起自己已经好久没有写博客了,突然间很有感触,想水一篇文章,跟小伙伴们分享一下我的经历。 二、自我介绍 我出生在广东潮汕地区的一个小城…...

正点原子驱动开发BUG(一)--SPI无法正常通信
目录 一、问题描述二、讲该问题的解决方案三、imx6ull的spi适配器驱动程序控制片选分析3.1 设备icm20608的驱动程序分析3.2 imx的spi适配器的驱动程序分析 四、BUG修复测试五、其他问题 一、问题描述 使用正点的im6ull开发板进行spi通信驱动开发实验的时候,主机无法…...

SpringBoot接入轻量级分布式日志框架GrayLog
1.前言 日志在我们日常开发定位错误,链路错误排查时必不可少,如果我们只有一个服务,我们可以只简单的通过打印的日志文件进行排查定位就可以,但是在分布式服务环境下,多个环境的日志统一收集、展示则成为一个问题。目…...

光电器件:感知光与电的桥梁
光电器件是电子工程领域的一个重要分支,主要研究光与电之间的相互转换。这些器件在许多领域都有广泛的应用,如通信、生物医学、军事等。 光电器件主要包括光电二极管、光电晶体管、光电倍增管等。这些器件的工作原理都是基于光电效应,即光子…...

Ceph入门到精通-smartctl 查看硬盘参数
smartctl 参数含义 Model Family: Toshiba s... Enterprise Capacity HDD Device Model: TOSHIBA MG08ACss Serial Number: sssssss LU WWN Device Id: 5 ss ss Firmware Version: 4303 User Capacity: 16,000,900,661,248 bytes [16.0 TB] Sector Sizes: 51…...

Module build failed: TypeError: this.getOptions is not a function
在使用webpack打包出现以上错误时,可能是你安装的css-loader和style-loader的版本过高。 我用的webpack版本是3.6.0 因此需要降低一下版本 在你编辑器终端输入以下命令: npm install css-loader3.6.0 npm install --save-dev style-loader1.00 然后接下…...

蓝牙电子价签芯片OM6626/OM628超低功耗替代NRF52832
电子价签应用简介 在全球零售业受到电商冲击、劳动力成本和周转率上升、消费者需求改变的行业背景下,电子价签、AI货架监控系统、自助结账设备、相关的方案将零售行业的发展带上智能化数字化的发展道路上。为企业与客户带来的更高效更便捷的消费体验。 蓝牙电子价…...
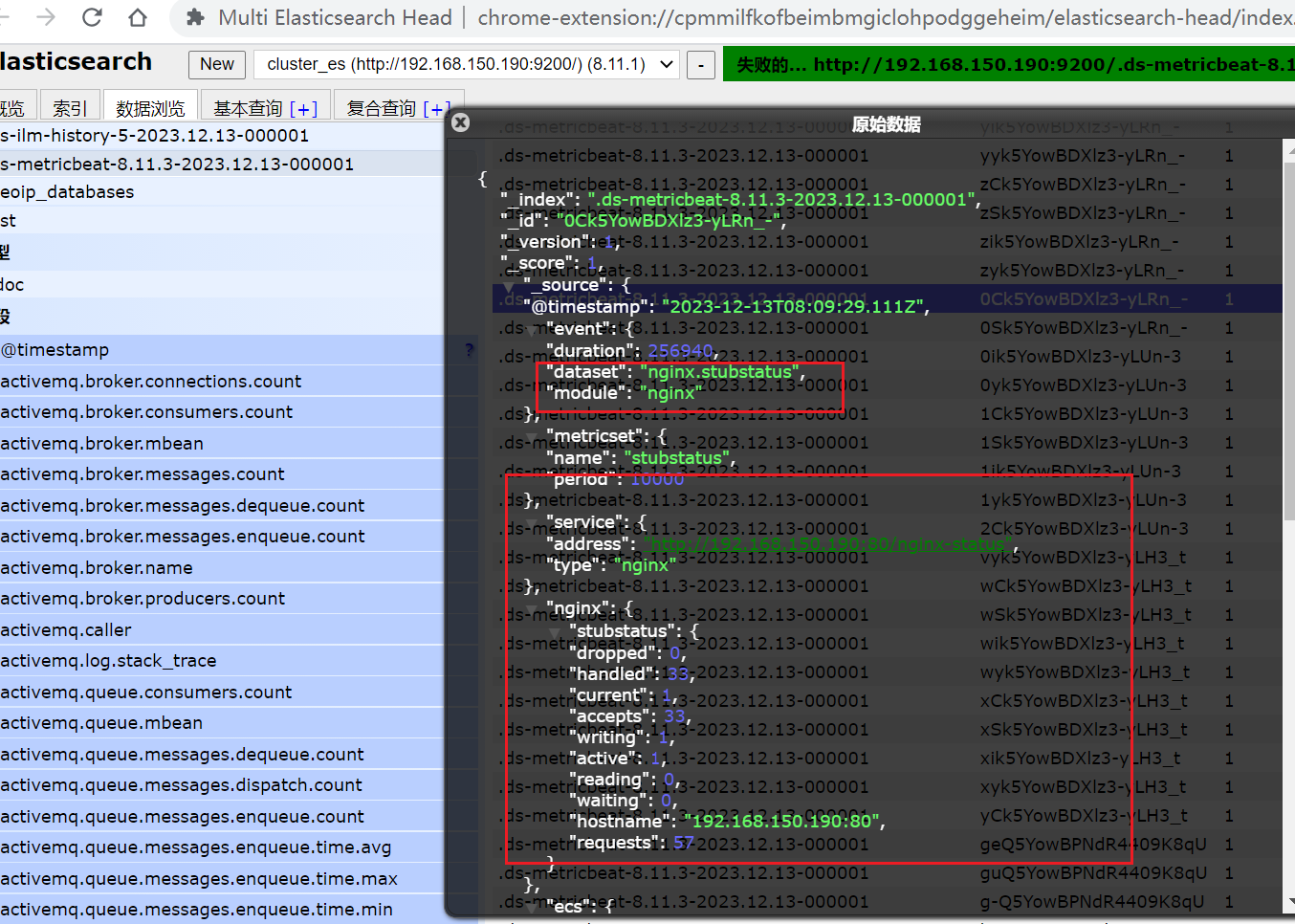
ELK(八)—Metricbeat部署
目录 介绍修改配置文件启动 Modulenginx开启状态查询配置Nginx module查看是否配置成功 介绍 Metricbeat 是一个轻量级的开源度量数据收集器,用于监控系统和服务。它由 Elastic 公司开发,并作为 Elastic Stack(Elasticsearch、Logstash、Kiba…...

Ansible自动化运维以及模块使用
ansible的作用: 远程操作主机功能 自动化运维(playbook剧本基于yaml格式书写) ansible是基于python开发的配置管理和应用部署工具。在自动化运维中,现在是异军突起 ansible能够批量配置、部署、管理上千台主机。类似于Xshell的一键输入工具。不需要每…...
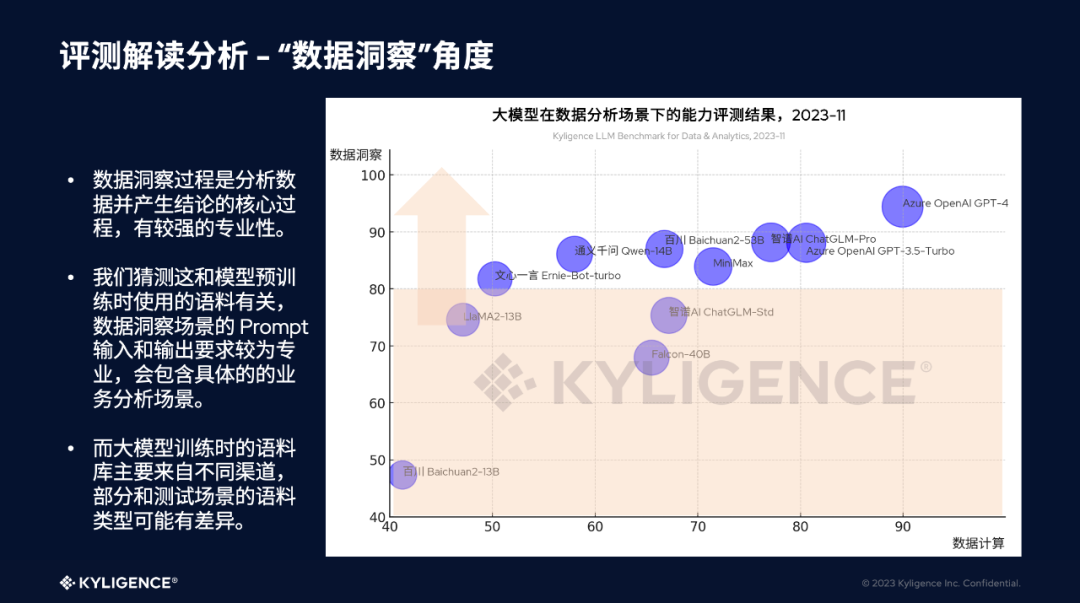
数据分析场景下,企业大模型选型的思路与建议
来源/作者:爱分析 随着大模型带来能力突破,让AI与数据分析相互结合,使分析结果更好支撑业务,促进企业内部数据价值释放,成为了当下企业用户尤为关注的话题。本次分享主要围绕数据分析场景下大模型底座的选型思路&#…...
Mongodb复制集架构
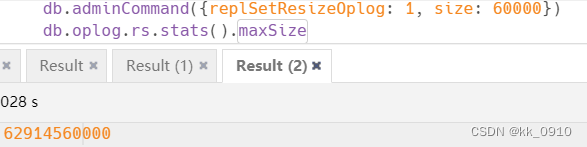
目录 复制集架构 复制集优点 复制集模式 复制集搭建 复制集常用命令 复制集增删节点 复制集选举 复制集同步 oplog分析 什么是oplog 查看oplog oplog大小 复制集架构 复制集优点 数据复制: 数据在Primary节点上进行写入,然后异步地复制到Secondary节点&a…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
