1112. 迷宫(DFS之连通性模型)
1112. 迷宫 - AcWing题库
一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 n∗n 的格点组成,每个格点只有2种状态,.和#,前者表示可以通行后者表示不能通行。
同时当Extense处在某个格点时,他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上,Extense想要从点A走到点B,问在不走出迷宫的情况下能不能办到。
如果起点或者终点有一个不能通行(为#),则看成无法办到。
注意:A、B不一定是两个不同的点。
输入格式
第1行是测试数据的组数 k,后面跟着 k 组输入。
每组测试数据的第1行是一个正整数 n,表示迷宫的规模是 n∗n 的。
接下来是一个 n∗n 的矩阵,矩阵中的元素为.或者#。
再接下来一行是 4 个整数 ha,la,hb,lb,描述 A 处在第 ha 行, 第 la 列,B 处在第 hb 行, 第 lb 列。
注意到 ha,la,hb,lb 全部是从 0 开始计数的。
输出格式
k行,每行输出对应一个输入。
能办到则输出“YES”,否则输出“NO”。
数据范围
1≤n≤100
输入样例:
2
3
.##
..#
#..
0 0 2 2
5
.....
###.#
..#..
###..
...#.
0 0 4 0
输出样例:
YES
NO解析 :
使用dfs进行判断代码要比bfs简洁
dfs代码:
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
using namespace std;
typedef long long LL;
const int N = 1e2 + 2;
int n, ha, la, hb, lb;
char str[N][N];
bool vis[N][N];
int dx[4] = { -1,0,1,0 }, dy[4] = { 0,1,0,-1 };
bool dfs(int x, int y) {if (str[x][y] == '#')return false;if (x == hb && y == lb)return true;for (int i = 0; i < 4; i++) {int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= n || b < 0 || b >= n)continue;if (vis[a][b])continue;vis[a][b] = 1;if (dfs(a, b))return true;}return false;
}int main() {int T;cin >> T;while (T--) {cin >> n;for (int i = 0; i < n; i++) {scanf("%s", str[i]);}cin >> ha >> la >> hb >> lb;memset(vis, 0, sizeof vis);if (dfs(ha, la))cout << "YES" << endl;else cout << "NO" << endl;}return 0;
}
BFS代码:
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
using namespace std;
typedef long long LL;
const int N = 1e2 + 2;
int n,ha,la,hb,lb;
char str[N][N];
typedef pair<int, int> PII;
bool vis[N][N];string bfs() {string ret1 = "YES", ret2 = "NO";if (str[ha][la] == '#' || str[hb][lb] == '#')return ret2;int dx[4] = { -1,0,1,0 }, dy[4] = { 0,1,0,-1 };memset(vis, 0, sizeof vis);queue<PII>q;q.push({ ha,la });vis[ha][la] = 1;while (!q.empty()) {auto t = q.front();q.pop();if (t.first == hb && t.second == lb)return ret1;for (int i = 0; i < 4; i++) {int a = t.first + dx[i], b = t.second + dy[i];if (a < 0 || a >= n || b < 0 || b >= n)continue;if (str[a][b] == '#'||vis[a][b])continue;vis[a][b] = 1;q.push({ a,b });}}return ret2;
}int main() {int T;cin >> T;while (T--) {cin >> n;for (int i = 0; i < n; i++) {scanf("%s", str[i]);}cin >> ha >> la >> hb >> lb;cout << bfs() << endl;}return 0;
}相关文章:
)
1112. 迷宫(DFS之连通性模型)
1112. 迷宫 - AcWing题库 一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 n∗n 的格点组成,每个格点只有2种状态,.和#,前者表示可以通行后者表示不能通行。 同时当Extense处在某个格点时,他只…...
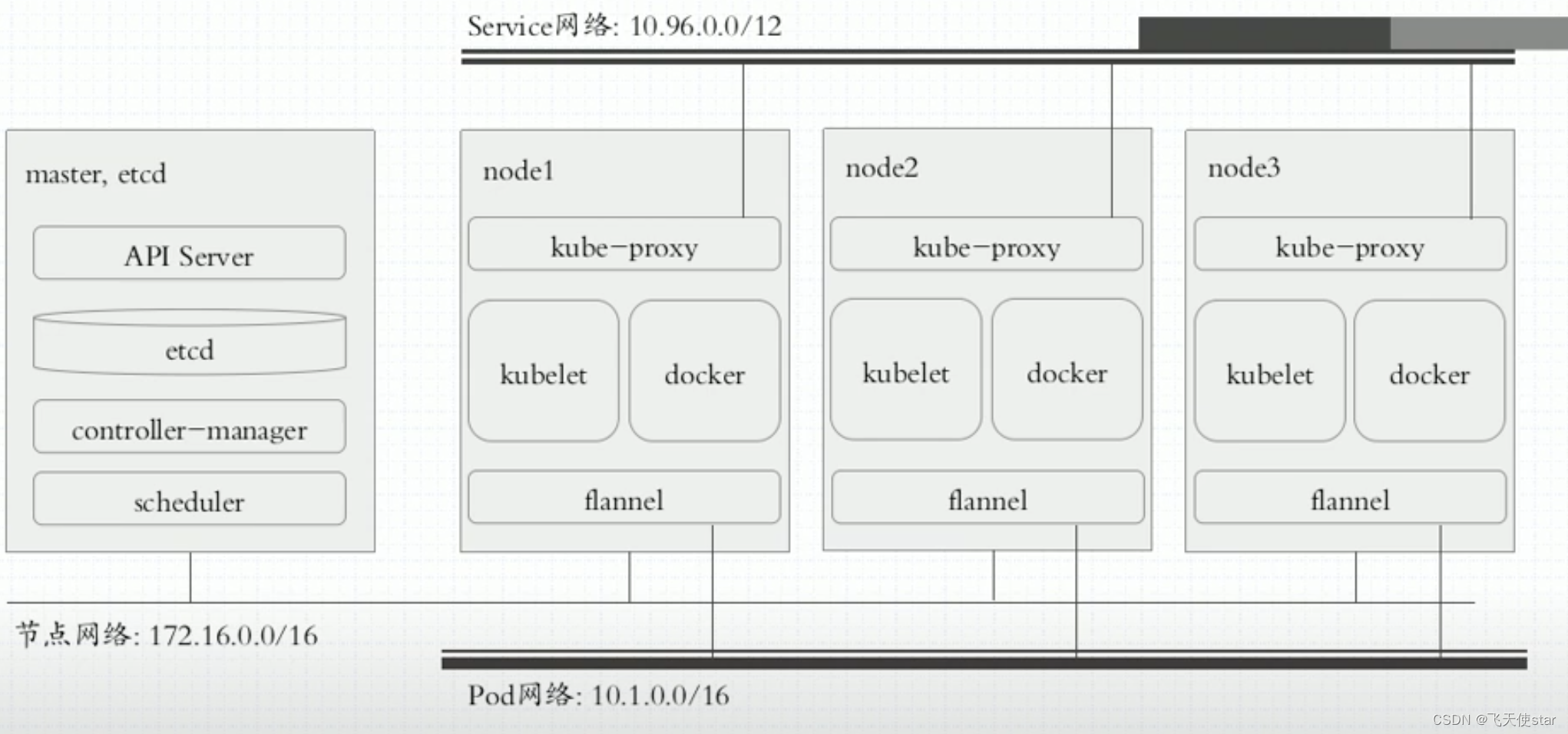
飞天使-k8s知识点1-kubernetes架构简述
文章目录 名词功能要点 k8s核心要素CNCF 云原生框架简介k8s组建介绍 名词 CI 持续集成, 自动化构建和测试:通过使用自动化构建工具和自动化测试套件,持续集成可以帮助开发人员自动构建和测试他们的代码。这样可以快速检测到潜在的问题,并及早…...
linux中deadline调度原理与代码注释
简介 deadline调度是比rt调度更高优先级的调度,它没有依赖于优先级的概念,而是给了每个实时任务一定的调度时间,这样的好处是:使多个实时任务场景的时间分配更合理,不让一些实时任务因为优先级低而饿死。deadline调度…...

jquery、vue、uni-app、小程序的页面传参方式
jQuery、Vue、Uni-app 和小程序(例如微信小程序)都有它们自己的页面传参方式。下面分别介绍这几种方式的页面传参方式: jQuery: 在jQuery中,页面传参通常是通过URL的查询参数来实现的。例如: <a href"page2…...
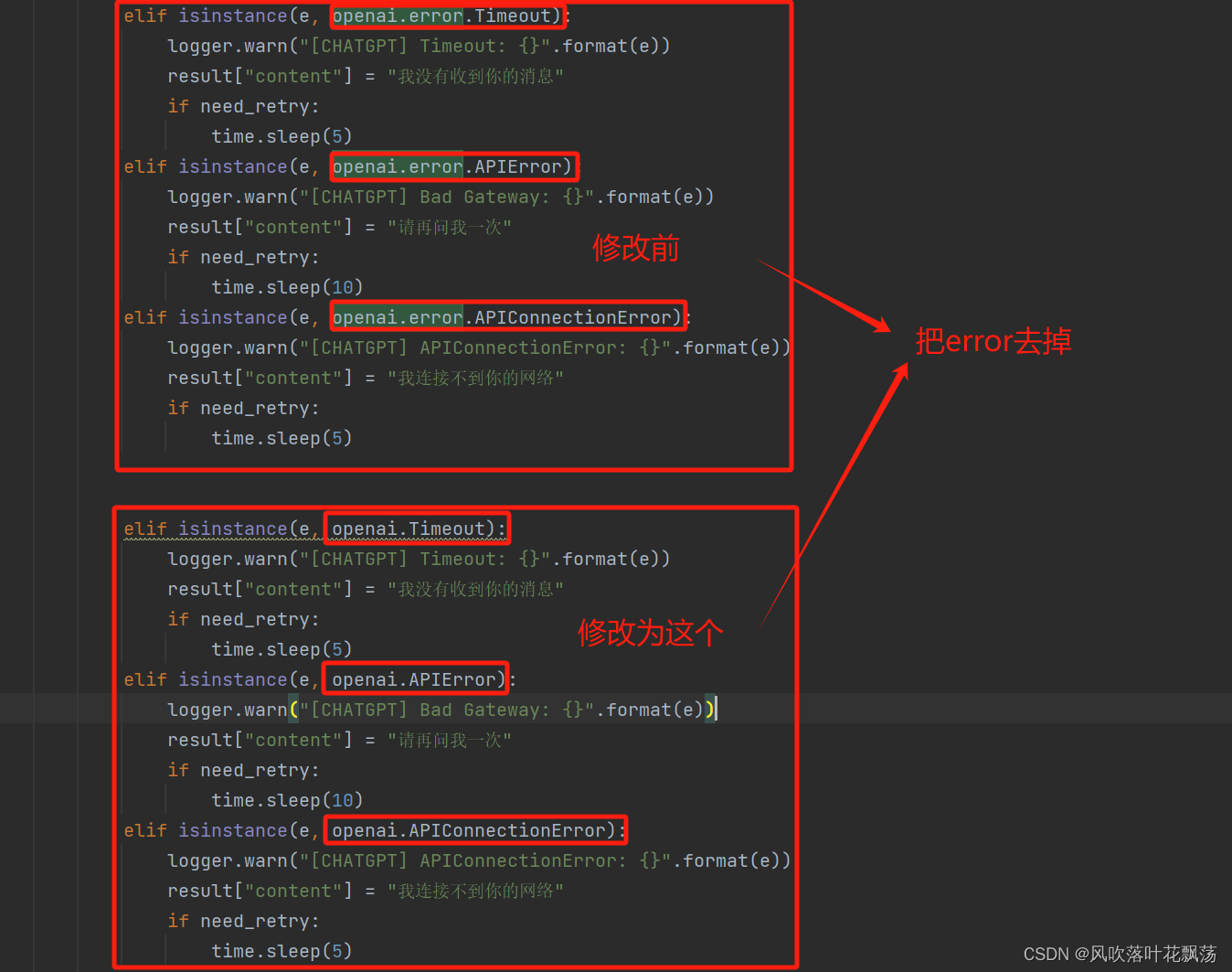
ModuleNotFoundError: No module named ‘openai.error‘
ModuleNotFoundError: No module named ‘openai.error’ result self.fn(*self.args, **self.kwargs) File “H:\chatGPTWeb\chatgpt-on-wechat\channel\chat_channel.py”, line 168, in _handle reply self._generate_reply(context) File “H:\chatGPTWeb\chatgpt-on-wec…...

理解pom.xml中的parent标签
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: 循序渐进学SpringBoot ✨特色专栏&…...
element ui el-avatar 源码解析零基础逐行解析
avatar功能介绍 快捷配置头像的样式 avatar 的参数配置 属性说明参数size尺寸type string 类型 (‘large’,‘medium’,‘small’)number类型 validator 校验shape形状circle (原型) square(方形)icon传入的iconsrc传入的图片st…...
Linux下c语言实现动态库的动态调用
在Linux操作系统下,有时候需要在不重新编译程序的情况下,运行时动态地加载库,这时可以通过Linux操作系统提供的API可以实现,涉及到的API主要有dlopen、dlsym和dlclose。使用时,需要加上头文件#include <dlfcn.h>…...
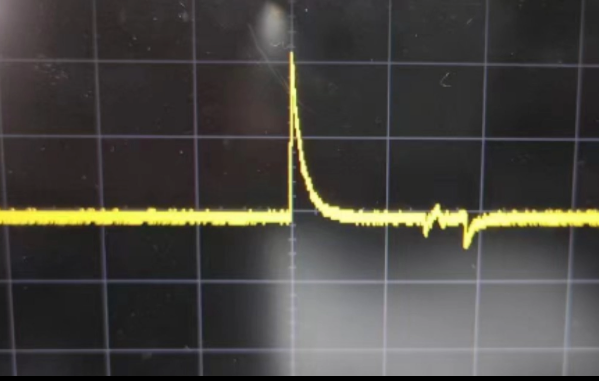
为什么MCU在ADC采样时IO口有毛刺?
大家在使用MCU内部ADC进行信号采样一个静态电压时,可能在IO口上看到这样的波形。这个时候大家一般会认识是信号源有问题,但仔细观察会发现这个毛刺的频率是和ADC触发频率一样的。 那么为什么MCU在ADC采样时IO口会出现毛刺呢?这个毛刺对结果有…...

C# 将 Word 转化分享为电子期刊
目录 需求 方案分析 相关库引入 关键代码 Word 转 Pdf Pdf 转批量 Jpeg Jpeg 转为电子书 实现效果演示 小结 需求 曾经的一个项目,要求实现制作电子期刊定期发送给企业进行阅读,基本的需求如下: 1、由编辑人员使用 Microsoft Word…...

网络世界的黑暗角落:常见漏洞攻防大揭秘
网络世界的黑暗角落:常见漏洞攻防大揭秘 今天带来了网站常见的漏洞总结,大家在自己的服务器上也需要好好进行防护,密码不要过于简单.不然非常容易遭到攻击,最终达到不可挽回的损失.很多黑客想网络乞丐一样将你服务器打宕机,然后要求你进行付费.不知道大家有没有遇到…...

通信领域发展方向
5G网络技术:随着5G网络的建设和商用推广,各家运营商、厂商和研究机构都在探索5G技术的应用场景和解决方案,如网络切片、毫米波通信、多用户MIMO等。 物联网技术:物联网技术已经成为通信行业的重点发展领域,包括传感器…...

21 3GPP中 5G NR高速列车通信标准化
文章目录 信道模型实验——物理层设计相关元素μ(与子载波间隔有关)设计参考信号(DMRS) 本文提出初始接入、移动性管理、线性小区设计等高层技术。描述3GPP采用HST场景的评估参数,阐释了HST应用的物理层技术,包括数字通信和参考信号设计,链路…...

【网络安全】-Linux操作系统—CentOS安装、配置
文章目录 准备工作下载CentOS创建启动盘确保硬件兼容 安装CentOS启动安装程序分区硬盘网络和主机名设置开始安装完成安装 初次登录和配置更新系统安装额外的软件仓库安装网络工具配置防火墙设置SELinux安装文本编辑器配置SSH服务 总结 CentOS是一个基于Red Hat Enterprise Linu…...
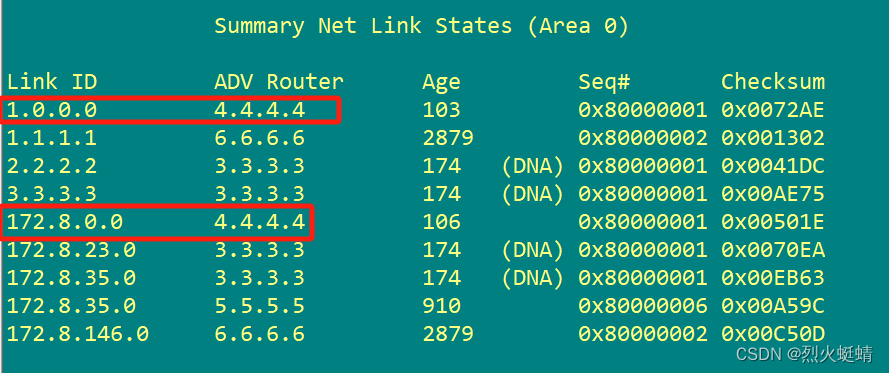
CCNP课程实验-OSPF-CFG
目录 实验条件网络拓朴需求 配置实现基础配置1. 配置所有设备的IP地址 实现目标1. 要求按照下列标准配置一个OSPF网络。 路由协议采用OSPF,进程ID为89 ,RID为loopback0地址。3. R4/R5/R6相连的三个站点链路OSPF网络类型配置成广播型,其中R5路…...
【Spring Security】打造安全无忧的Web应用--入门篇
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于Spring Security的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.Spring Security是什么 1.概…...
【每日一题】【12.20】2828.判别首字母缩略词
🔥博客主页: A_SHOWY🎥系列专栏:力扣刷题总结录 数据结构 云计算 数字图像处理 力扣每日一题_ 1.题目链接 2828. 判别首字母缩略词https://leetcode.cn/problems/check-if-a-string-is-an-acronym-of-words/ 2.题目描述 今天…...
LabVIEW开发振动数据分析系统
LabVIEW开发振动数据分析系统 自动测试系统基于LabVIEW平台设计,采用了多种高级硬件设备。系统的硬件组成包括PCB振动加速度传感器,这是一种集成了传统压电加速度传感器和电荷放大器的先进设备,能够直接与采集仪器连接。此外,系统…...

去掉乘法运算的加法移位神经网络架构
[CVPR 2020] AdderNet: Do We Really Need Multiplications in Deep Learning? 代码:https://github.com/huawei-noah/AdderNet/tree/master 核心贡献 用filter与input feature之间的L1-范数距离作为“卷积层”的输出为了提升模型性能,提出全精度梯度…...

【TB作品】51单片机,具有报时报温功能的电子钟
2.具有报时报温功能的电子钟 一、功能要求: 1.显示室温。 2.具有实时时间显示。 3.具有实时年月日显示和校对功能。 4.具有整点语音播报时间和温度功能。 5.定闹功能,闹钟音乐可选。 6.操作简单、界面友好。 二、设计建议: 1.单片机自选(C51、STM32或其他单片机)。 2.时钟日历芯…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
