Debian系统设置SSH密钥登陆
如果没有安装ssh,root权限运行apt install openssh-server进行安装。
ssh-keygen -t rsa # 生成配对密钥,后续一路enter即可
会在用户目录(即~这个)下生成.ssh文件夹,里面的id_rsa是私钥,id_rsa.pub是公钥。
输入cd ~/.ssh/进入.ssh文件夹中,将公钥写入到authorized_keys中,将id)rsa下载并保存好。
touch authorized_keys
cat id_rsa.pub >> authorized_keys # 写入公钥写入
此时,还需要给文件相应的权限,不然可能无法正常工作
chmod 600 authorized_keys
chmod 700 ~/.ssh
现在密钥已经配对好了,还需要修改ssh的配置文件,打开/etc/ssh/sshd_config文件,修改其中的关键文件
PubkeyAuthentication yes # yes表示允许密钥登陆
AuthorizedKeysFile .ssh/authorized_keys .ssh/authorized_keys2 # 指定密钥的文件位置
PasswordAuthentication no # 不允许使用密码登陆,等测试密钥登陆成功了再修改此条,以防无法登陆
到此,SSH密钥登陆就配置完成了,重启ssh服务即可
systemctl restart ssh
除此之外,我习惯性更改端口,并且禁止root用户用户登陆
Port 12345 # 把默认的22端口改了
PermitRootLogin no # 禁止root用户登陆
相关文章:

Debian系统设置SSH密钥登陆
如果没有安装ssh,root权限运行apt install openssh-server进行安装。 ssh-keygen -t rsa # 生成配对密钥,后续一路enter即可会在用户目录(即~这个)下生成.ssh文件夹,里面的id_rsa是私钥,id_rsa.pub是公钥…...

uniapp cli开发和HBuilderX开发
uniapp cli开发和HBuilderX开发 前言 uniapp是一个跨平台的开发框架,可以开发出微信小程序、支付宝小程序、百度小程序、头条小程序、H5、App等,开发者只需要写一套代码,就可以发布到各个平台,大大提高了开发效率。 uniapp的开…...
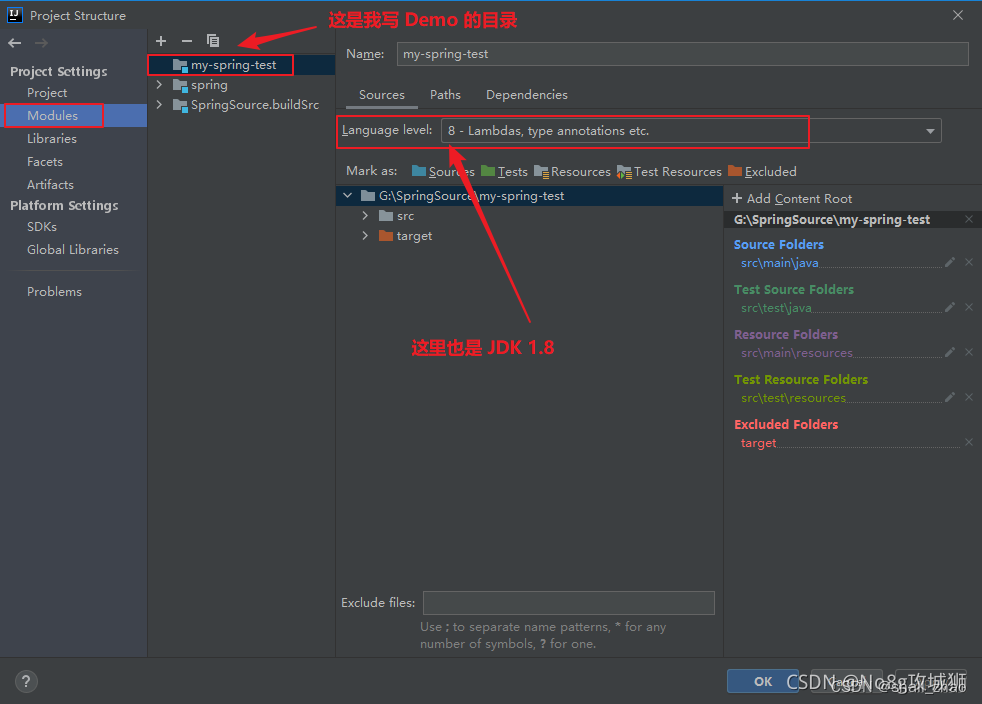
【Java异常】idea 报错:无效的目标发行版:17 的解决办法
【Java异常】idea 报错:无效的目标发行版:17 的解决办法 一,问题来源 springcloud的第一个demo项目就给我干趴了 二、原因分析 java: 无效的目标发行版: 17 原因就是 JDK 版本不对。从 IDEA 编辑器中可以找到问题的原因所在,…...

代码提交规范-ESLint+Prettier+husky+Commitlint
代码提交规范-ESLintPrettierhuskyCommitlint 配置eslint (3步)配置prettier(4步)1.安装配置prettier2.设置忽略文件 .prettierignore3.处理eslint冲突4. 配置vscode 的settings.json husky安装并配置lint-staged(3步)安装配置com…...
)
手动实现 Vue 3的简易双向数据绑定(模仿源码)
Vue 3 带来了许多令人兴奋的新特性和改进,其中之一就是其双向数据绑定的实现方式。与 Vue 2 使用 Object.defineProperty 不同,Vue 3 利用了 JavaScript 的 Proxy 特性来创建响应式数据。在这篇博客中,我们将探讨 Vue 3 中双向数据绑定的基础…...
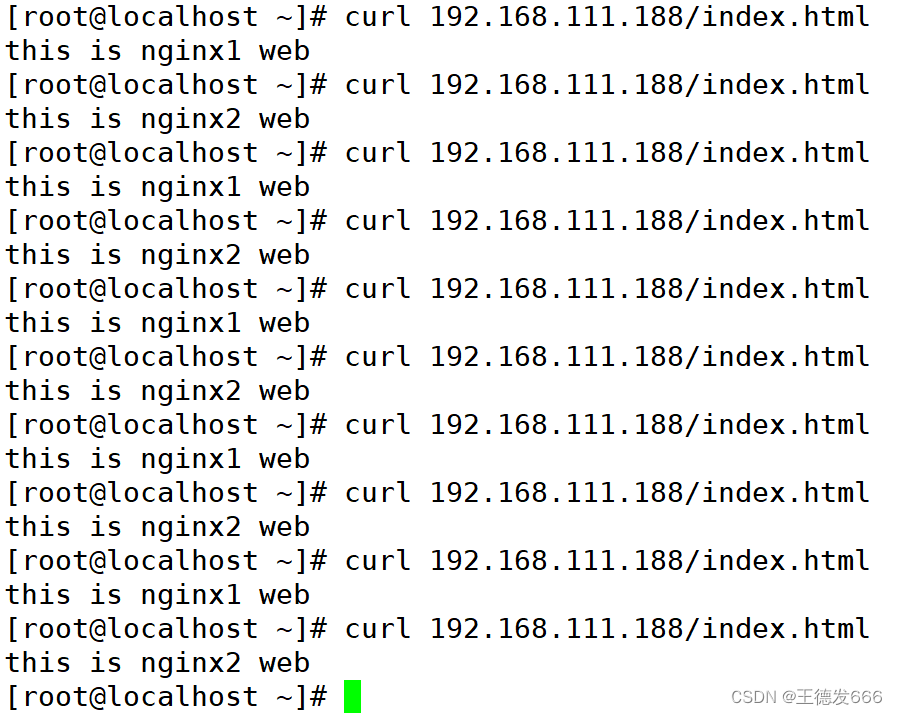
LVS最终奥义之DR直接路由模式
1 LVS-DR(直接路由模式) 1.1 LVS-DR模式工作过程 1.客户端通过VIP将访问请求报文(源IP为客户端IP,目标IP为VIP)发送到调度器 2.调度器通过调度算法选择最适合的节点服务器并重新封装数据报文(将源mac地址改为调度器的mac地址&am…...
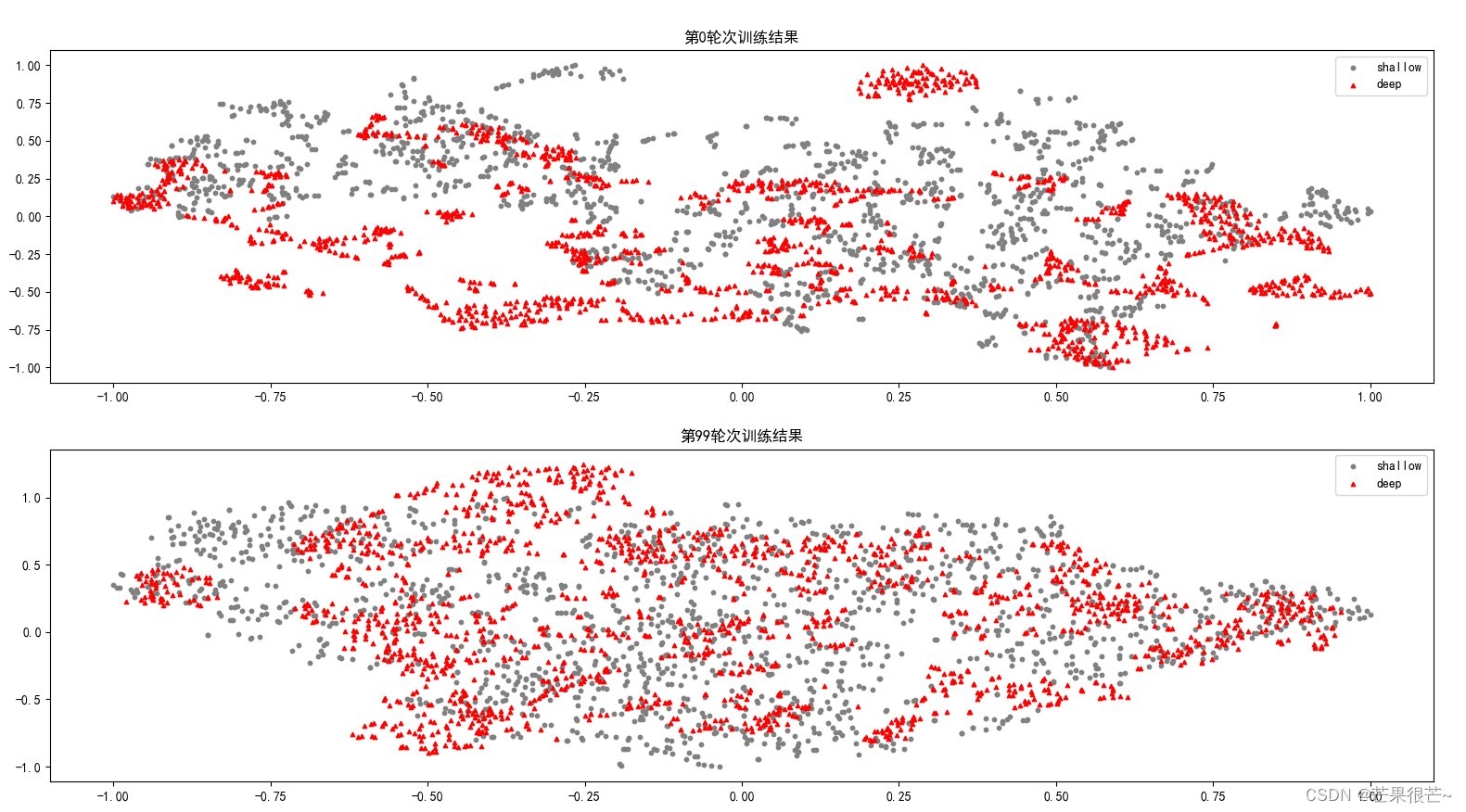
t-SNE高维数据可视化实例
t-SNE:高维数据分布可视化 实例1:自动生成一个S形状的三维曲线 实例1结果: 实例1完整代码: import matplotlib.pyplot as plt from sklearn import manifold, datasets """对S型曲线数据的降维和可视化"&q…...

配置应用到k8s
配置应用到k8s,前置条件是安装了Docker,Minikube,kubectl 应用已经通过Docker生成本地镜像文件 1,创建godemo-deployment.yaml apiVersion: apps/v1kind: Deploymentmetadata:name: godemo-deploymentspec:replicas: 3 #启动三个…...

(四)STM32 操作 GPIO 点亮 LED灯 / GPIO工作模式
目录 1. STM32 工程模板中的工程目录介绍 2. GPIO 简介 3. GPIO 框图剖析 1)保护二极管及上、下拉电阻 2) P-MOS 管和 N-MOS 管 3)输出数据寄存器 3.1)ODR 端口输出数据寄存器 3.2)BSRR 端口位设置/清除寄存器 4&a…...
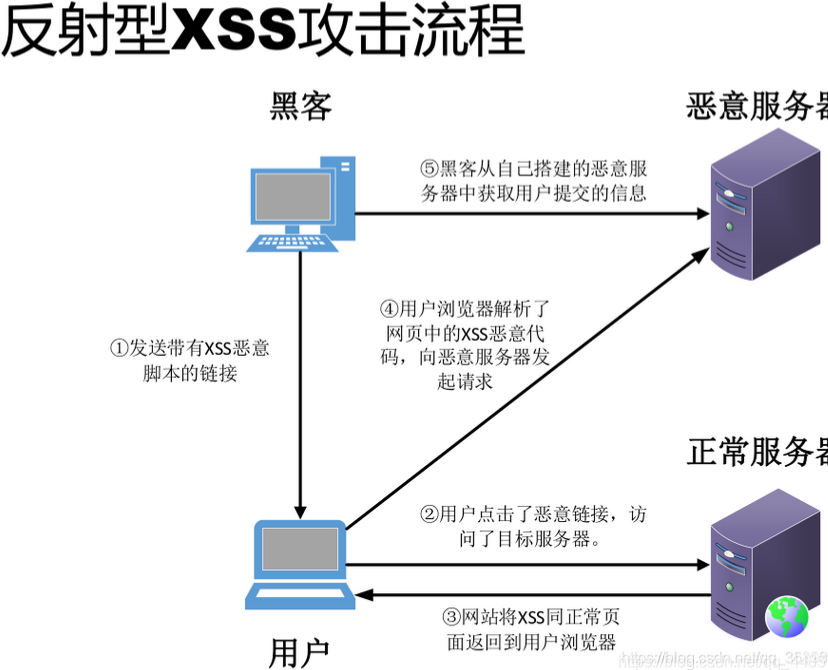
你知道跨站脚本攻击吗?一篇带你了解什么叫做XSS
1.XSS简介 (1)XSS简介 XSS作为OWASP TOP 10之一。 XSS中文叫做跨站脚本攻击(Cross-site scripting),本名应该缩写为CSS,但是由于CSS(Cascading Style Sheets,层叠样式脚本&#x…...
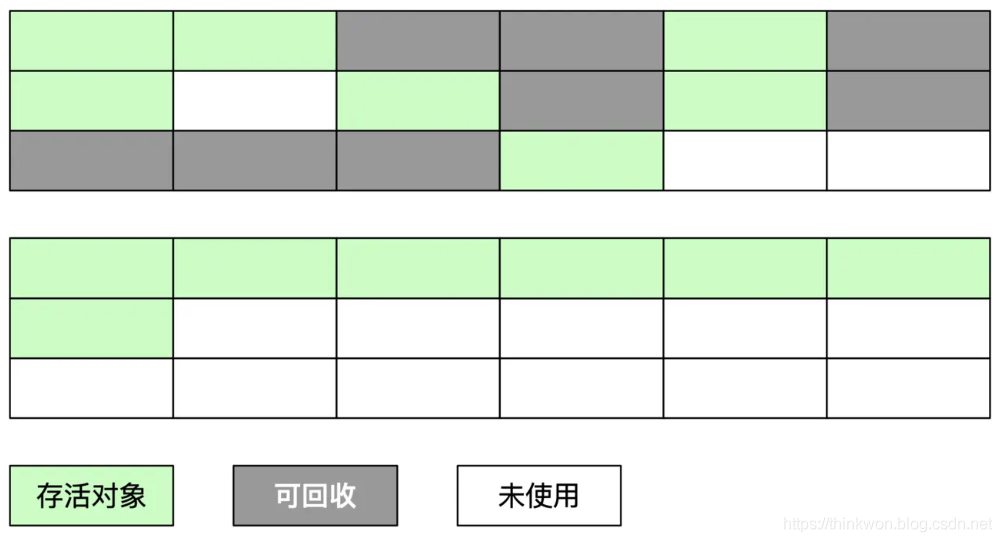
JVM入门
JVM概述 JVM位置 JVM体系结构 注意:栈中一定不存在垃圾,栈中数据用完一个弹出一个,总结来说,栈区、本地方法栈、程序计数器这三块必定不存在垃圾。JVM调优主要是针对方法区、堆(99%)进行调优。 常用的第三…...
)
Cmake基础(5)
这篇文章主要描述如何使用cmake构建一个库工程 文章目录 add_libraryinstall 库工程的代码:头文件和源文件 #ifndef ADD_H #define ADD_H#ifdef _WIN32 #ifdef MYMATH_EXPORTS #define MYMATH_API __declspec(dllexport) #else #define MYMATH_API __declspec(dll…...

Rabbitmq 死信取消超时订单
本文使用的版本 otp_win64_25.0rabbitmq-server-3.11.26rabbitmq插件 rabbitmq_delayed_message_exchange-3.11.1 pom.xml文件 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId> …...

C语言—每日选择题—Day55
指针相关博客 打响指针的第一枪:指针家族-CSDN博客 深入理解:指针变量的解引用 与 加法运算-CSDN博客 第一题 1. 若有如下定义,则 p1&m;p2p1; 是正确赋值语句.说法是否正确? int *p1; int *p2; int m …...

软件测试岗位的简历怎么写?项目怎么包装
已经帮大家打包好了包装好的简历模板,大家可以直接进行套用,详情请望下看 自动化测试相关教程推荐: 2023最新自动化测试自学教程新手小白26天入门最详细教程,目前已有300多人通过学习这套教程入职大厂!!_哔哩哔哩_bili…...

服务器解析漏洞是什么?攻击检测及修复
服务器解析漏洞(Server-side Include Vulnerability,SSI漏洞)是一种安全漏洞,通常出现在支持服务器端包含(SSI)功能的Web服务器上。SSI是一种在Web页面中嵌入动态内容的技术,允许开发人员将外部…...

HTML---CSS美化网页元素
文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 一.div 标签: <div>是HTML中的一个常用标签,用于定义HTML文档中的一个区块(或一个容器)。它可以包含其他HTML元素,如文本、图像…...

【Docker】基础篇
文章目录 Docker为什么出现容器和虚拟机关于虚拟机关于Docker二者区别: Docker的基本组成相关概念-镜像,容器,仓库安装Docker卸载docker阿里云镜像加速docker run的原理**为什么容器比虚拟机快**Docker的常用命令1.帮助命令2.镜像相关命令3.容…...
Potplayer播放器远程访问群晖WebDav本地资源【内网穿透】
文章目录 本教程解决的问题是:按照本教程方法操作后,达到的效果是:1 使用环境要求:2 配置webdav3 测试局域网使用potplayer访问webdav3 内网穿透,映射至公网4 使用固定地址在potplayer访问webdav 国内流媒体平台的内容…...

【神经网络】imshow展示图片报错
文章目录 代码示例报错信息报错原因解决方法其他问题 代码示例 plt.imshow(np.squeeze(images[0]))报错信息 Invalid shape (3, 60, 90) for image data报错原因 格式错误,输入具有RGB值的图像,输入三维数组参数的格式应该是(高度…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
