关于with torch.no_grad:的一些小问题
with torch.no_grad:是截断梯度记录的,新生成的数据的都不记录梯度,但是今天产生了一点小疑惑,如果存在多层函数嵌入,是不是函数内所有的数据都不记录梯度,验证了一下,确实是的。
import torch
x = torch.randn(10, 5, requires_grad = True)
y = torch.randn(10, 5, requires_grad = True)
z = torch.randn(10, 5, requires_grad = True)
def add(x,y,z):w = x + y + zprint(w.requires_grad)print(w.grad_fn)
def add2(x,y,z):add(x,y,z)
with torch.no_grad():add2(x,y,z)add2(x,y,z)
“”“
输出:
False
None
True
<AddBackward0 object at 0x00000250371BED68>
”“”
相关文章:

关于with torch.no_grad:的一些小问题
with torch.no_grad:是截断梯度记录的,新生成的数据的都不记录梯度,但是今天产生了一点小疑惑,如果存在多层函数嵌入,是不是函数内所有的数据都不记录梯度,验证了一下,确实是的。 import torch x torch.r…...
大创项目推荐 深度学习 机器视觉 人脸识别系统 - opencv python
文章目录 0 前言1 机器学习-人脸识别过程人脸检测人脸对其人脸特征向量化人脸识别 2 深度学习-人脸识别过程人脸检测人脸识别Metric Larning 3 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习 机器视觉 人脸识别系统 该项目…...

【PostGIS】空间数据库-常用空间函数
记录一些常用的空间函数: 1、转换函数 在几何图形和外部数据格式之间进行转换的函数。 -- 将文本表示转换为几何类型 -- 结果:0101000000000000000000F03F000000000000F03F SELECT st_geomfromtext(point(1 1),0);-- 将几何类型转换为文本表示 -- 结果…...
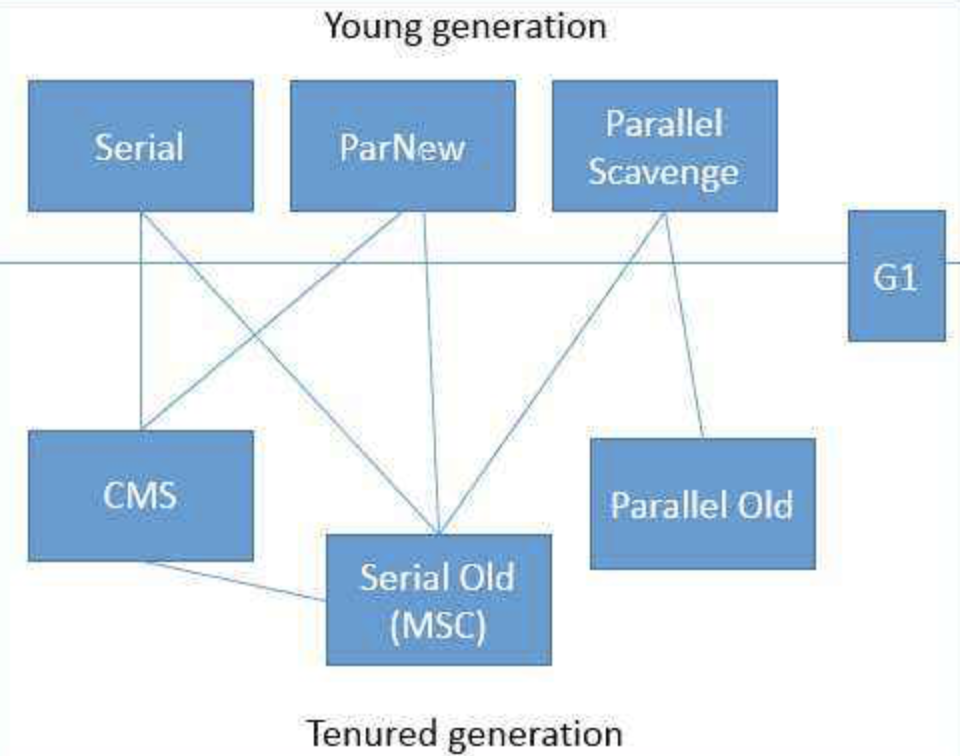
程序员的50大JVM面试问题及答案
文章目录 1.JDK、JRE、JVM关系?2.启动程序如何查看加载了哪些类,以及加载顺序?3. class字节码文件10个主要组成部分?4.画一下jvm内存结构图?5.程序计数器6.Java虚拟机栈7.本地方法栈8.Java堆9.方法区10.运行时常量池?…...

架构设计系列之前端架构和后端架构的区别和联系
前端架构和后端架构都是软件系统中最关键的架构层,负责处理不同方面的任务和逻辑,两者之间是存在一些区别和联系的,我会从以下几个方面来阐述: 一、定位和职责 前端架构 主要关注用户界面和用户体验,负责处理用户与…...
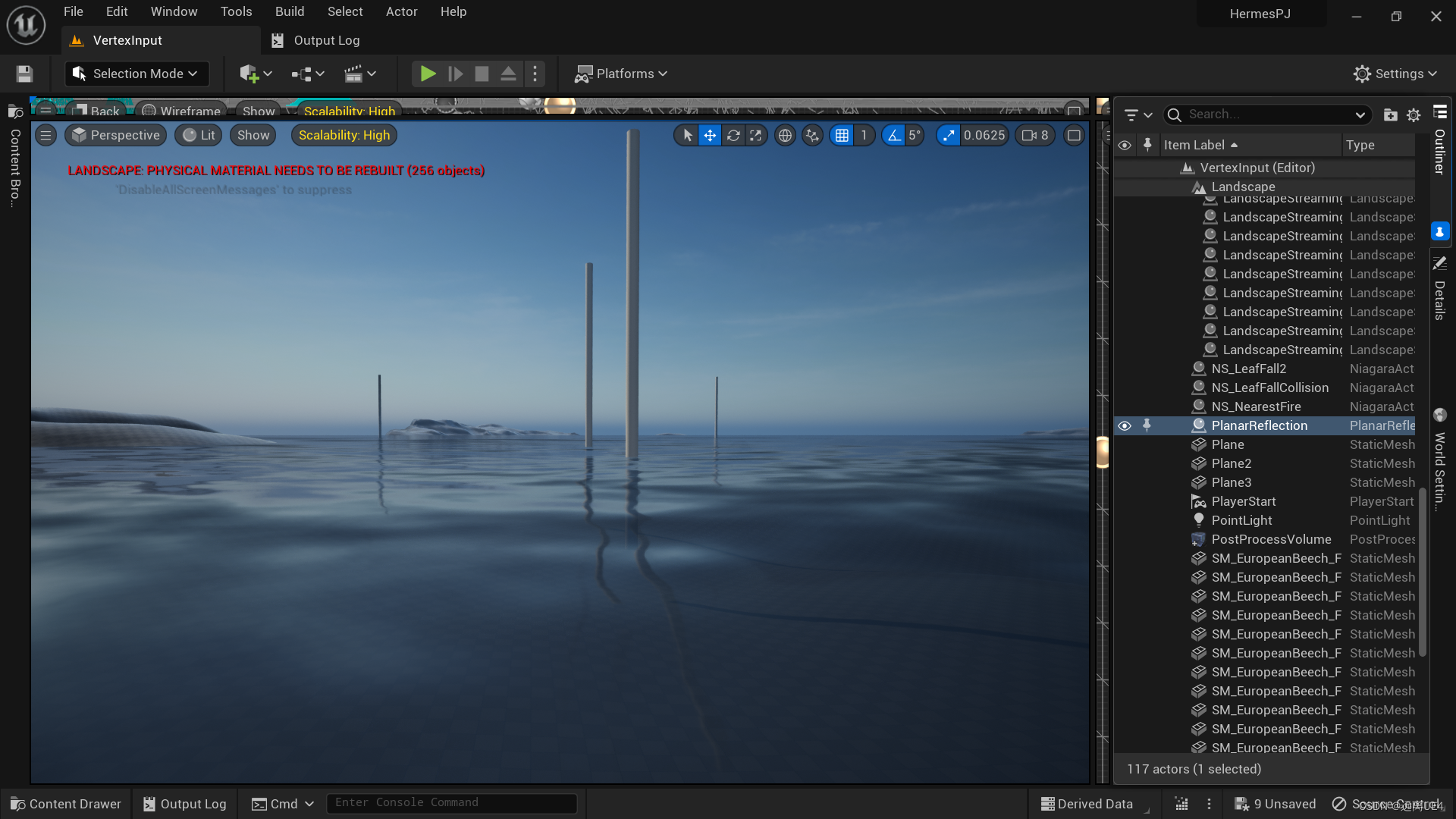
UE5 水材质注意要点
1、两个法线反向交替流动,可以去观感假的现象 2、水面延边的透明度低 3、增加水面延边的浪花 4、增加折射 折射要整体质量至少在High才有效果 改为半透明材质没有法线信息? 5、处理反射效果 勾选为true 找到这个放在水域 勾为false,即可有非…...

数据安全扫描仪荣膺网络安全优秀创新成果大赛优胜奖 - 凸显多重优势
近日,由中国网络安全产业联盟(CCIA)主办、CCI数据安全工作委员会中国电子技术标准化研究院等单位承办的“2023年网络安全优秀创新成果大赛”获奖名单公布。天空卫士数据安全扫描仪(DSS)产品获得创新成果大赛优胜奖。 本…...

数据结构学习 leetcode64最小路径和
动态规划 题目: 建议看这里,有这道题详细的解析。我觉得写的挺好。 这是我在学动态规划的时候,动手做的一道题。 虽然我在学动态规划,但是我之前学了dps,所以我就想先用dps试着做,结果发现不行…...
导出(导入)Linux虚拟机并修改IP地址
一、导出虚拟机 说明:先关闭虚拟机,然后再进行导出。 步骤1:选择要导出的虚拟机 步骤2:选择文件菜单栏下的导出为OVF文件。 步骤3:将导出的文件保存至硬盘文件夹。 二、导入虚拟机 步骤1:选择文件菜单栏…...

OpenCV4工业缺陷检测的六种方法
👨🎓博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 🐋 希望大家多多支…...
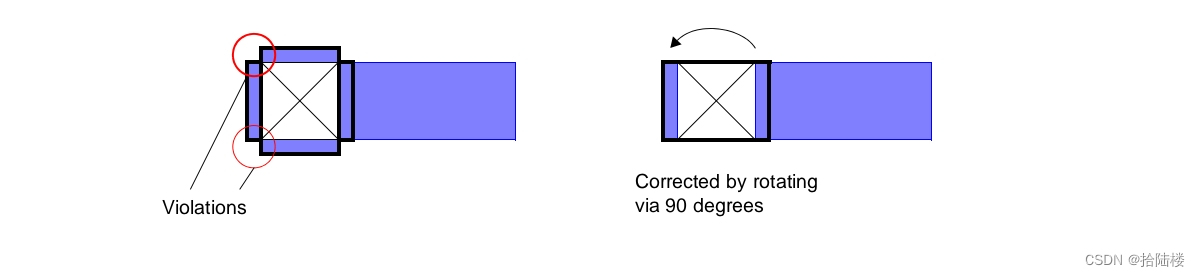
ICC2:Less than minimum edge length和Concave convex edge enclosure
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧? 拾陆楼知识星球入口 首先,要介绍一下这两种drc Less than minimum edge length对应的tf rule如下: 而Concave convex edge enclosure对应图示和tf 规则如下,可...
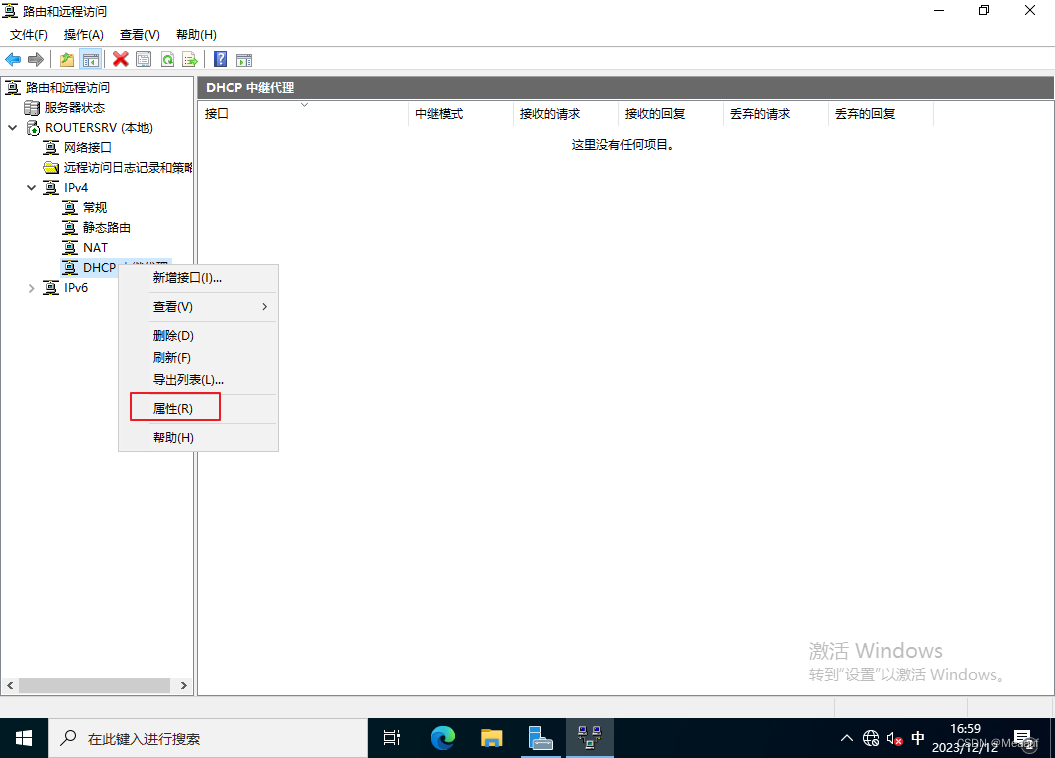
RouterSrv-DHCP
2023年全国网络系统管理赛项真题 模块B-Windows解析 题目 安装和配置DHCP relay服务,为办公区域网络提供地址上网。DHCP服务器位于AppSrv服务器上。拆分DHCP服务器上的作用域,拆分的百分比为7:3。InsideCli优先从RouterSrv获取地址。配置步骤 安装和配置DHCP relay服务,为办…...
文件的读写和过滤器)
【人生苦短,我学 Python】(8)文件的读写和过滤器
目录 简述 / 前言1. 文件的操作2. 过滤器2.1 more —— 逐屏显示数据2.2 sort —— 排序2.3 more 和 sort 一起用 文章传送门 简述 / 前言 上一篇我们介绍了 Python 的输入(input)和输出(print),以及如何通过命令行给…...

智能优化算法应用:基于饥饿游戏算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于饥饿游戏算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于饥饿游戏算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.饥饿游戏算法4.实验参数设定5.算法结果6.…...

leetCode算法—10. 正则表达式匹配
10.给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。 难度:困难 *** 给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。 ‘.’ 匹配任意单个字符 ‘*’ 匹…...
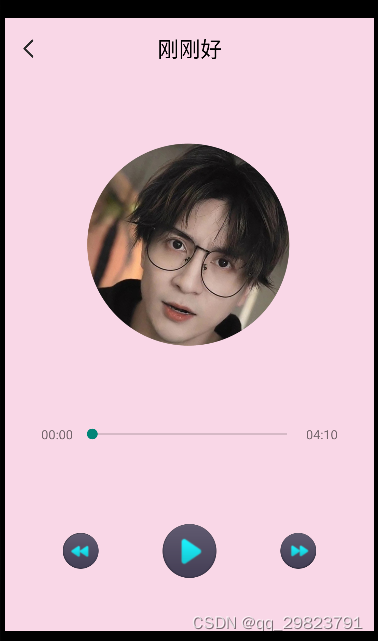
Android Studio 实现音乐播放器
目录 一、引言 视频效果展示: 1.启动页效果 2.登录页效果 3.注册页效果 4.歌曲列表页效果 5.播放页效果 二、详细设计 1.登陆注册功能 2.音乐列表页面 2.音乐播放功能 三、源码获取 一、引言 Android初学者开发第一个完整的实例项目应该就属《音乐播放器…...
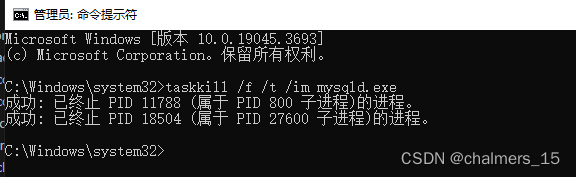
端口占用命令 netstat (centos)+netstat (windows)
linux 1.使用 netstat 命令查看端口占用情况 netstat -tlnp 使用 -p 选项查看进程信息。 使用 -t 选项列出 TCP 协议的连接:类似(使用 -u 选项列出 UDP 协议的连接:) 2.查找占用指定端口号的应用信息 netstat -tlnp | grep 3…...
Python-基于fastapi实现SSE流式返回(类似GPT)
最近在做大模型对话相关功能,需要将对话内容流式返回给前端页面(类似GPT的效果)。下面直接说下如何实现: 1.首先导入fastapi和sse流式返回所需要的包 from fastapi import APIRouter, Response, status from sse_starlette.sse …...

iOS中宿主APP与录屏扩展进程数据传递方式
背景 在iOS生态系统中,应用程序的功能不再局限于单一的宿主应用,而是可以通过扩展进程实现更丰富的用户体验和功能。其中一种引人注目的扩展是录屏功能,它使用户能够捕捉设备屏幕上的活动,无论是游戏过程、教育演示还是其他应用场…...

Windows系统下的可用RADIUS软件-[资源]
RADIUS协议相关原理介绍,可参考博客RADIUS协议原理介绍报文分析配置指导-RFC2865/RFC2866。 本文用于提供和介绍Window系统下几种可用的RADIUS软件。主要涉及软件有radius_ping(绿色免安装版)和WinRadius(绿色免安装版)…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
