图论 | 网络流的基本概念
文章目录
- 流网路
- 残留网络
- 增广路径
- 割
- 最大流最小割定理
- 最大流
- Edmonds-Karp 算法
- 算法步骤
- 程序代码
- 时间复杂度
流网路
流网络: G = ( V , E ) G = (V, E) G=(V,E)

- 有向图,不考虑反向边
- s:源点
- t:汇点
- c ( u , v ) c(u, v) c(u,v):边的最大容量
- 可行流 f f f
- 容量限制: 0 ≤ f ( u , v ) ≤ c ( u , v ) 0 \leq f(u, v) \leq c(u, v) 0≤f(u,v)≤c(u,v)
- 流量守恒:除了源点和汇点,所有点满足 流入 = 流出 流入 = 流出 流入=流出
- ∣ f ∣ |f| ∣f∣:可行流的流量,即从源点流向汇点的速率。一种通用的解释是 从源点流出的流量 − 流入源点的流量 从源点流出的流量 - 流入源点的流量 从源点流出的流量−流入源点的流量
- 最大流:最大可行流
残留网络
残留网络定义:一个可行流流网络 f f f 对应一个残留网络 G f G_f Gf
- 点集:与原图的点集一样 V f = V V_f = V Vf=V
- 边集:不仅包含原图的边,同时包含所有边的方向边,即 E f = E 和 E 中的所有反向边 E_f = E 和 E中的所有反向边 Ef=E和E中的所有反向边
- 边的容量: c f ( u , v ) c_f(u, v) cf(u,v)
- 原图中的边:剩下的容量,即 c ( u , v ) − f ( u , v ) c(u, v) - f(u, v) c(u,v)−f(u,v)
- 反向边:可以退回的流量,即 f ( v , u ) f(v, u) f(v,u)
重要结论:原网络的可行流 f f f 加上可行流对应的残留网络 G f G_f Gf,也是一个可行流
- 对应边相加:若方向同则相加;若反向反则相减
- 结论: ∣ f + f ′ ∣ = ∣ f ∣ + ∣ f ′ ∣ |f + f'| = |f| + |f'| ∣f+f′∣=∣f∣+∣f′∣
- 进一步,若残留网络没有可行流,那么原网络的可行流就一定是最大流
增广路径
在残留网络里,如果沿着容量大于 0 的边走,能走到汇点,则这条路径叫做增广路径
- 若存在一个增广路径,根据 ∣ f + f ′ ∣ = ∣ f ∣ + ∣ f ′ ∣ |f + f'| = |f| + |f'| ∣f+f′∣=∣f∣+∣f′∣,原来的可行流一定不是最大流
- 若不存在增广路径,我们可以得出当前可行流就是最大流
割
将点集 V 分成 S 和 T 两个子集
- 分割要满足 S ∪ T = V , S ∩ T = ∅ S ∪ T = V, S ∩ T = \emptyset S∪T=V,S∩T=∅
- 点集不一定连通
割的容量: c ( S , T ) = ∑ u ∈ S ∑ v ∈ T c ( u , v ) c(S, T) = \sum_{u ∈ S} \sum_{v ∈ T} c(u, v) c(S,T)=∑u∈S∑v∈Tc(u,v)
- 最小割:最小割的容量
- 割的容量不考虑反向边
割的流量: f ( S , T ) = ∑ u ∈ S ∑ v ∈ T f ( u , v ) − ∑ u ∈ T ∑ v ∈ S f ( u , v ) f(S, T) = \sum_{u ∈ S} \sum_{v ∈ T} f(u, v) - \sum_{u ∈ T} \sum_{v ∈ S} f(u, v) f(S,T)=∑u∈S∑v∈Tf(u,v)−∑u∈T∑v∈Sf(u,v)
- 流过去的流量减去流过来的流量
- 割的流量考虑反向边
重要性质:
-
对于任意一个割,割的流量一定小于等于割的容量,即 f ( S , T ) ≤ c ( S , T ) f(S, T) \leq c(S, T) f(S,T)≤c(S,T)
-
割的流量等于原流网络的流量,即 f ( S , T ) = ∣ f ∣ f(S,T) = |f| f(S,T)=∣f∣
-
f ( X , Y ) = − f ( Y , X ) f(X, Y) = -f(Y, X) f(X,Y)=−f(Y,X)
-
f ( Z , X ∪ Y ) = f ( Z , X ) + f ( Z , Y ) f(Z, X ∪ Y) = f(Z, X) + f(Z, Y) f(Z,X∪Y)=f(Z,X)+f(Z,Y)
-
f ( X ∪ Y , Z ) = f ( X , Z ) + f ( Y , Z ) f(X ∪ Y, Z) = f(X, Z) + f(Y, Z) f(X∪Y,Z)=f(X,Z)+f(Y,Z)
最大流最小割定理
以下三个条件是等价的
- 可行流 f f f 是最大流
- 可行流 f f f 的残留网络中不存在增广路
- 存在某个割 [ S , T ] [S, T] [S,T], ∣ f ∣ = c ( S , T ) |f| = c(S, T) ∣f∣=c(S,T)
最大流
Edmonds-Karp 算法
算法步骤
维护流网络的残留网络,不断进行以下流程:
- 找一条增广路 f ′ f' f′:可以用 BFS 进行搜索
- 更新残留网络 G f → G f + f ′ G_f → G_{f + f'} Gf→Gf+f′
程序代码
#include <iostream>
#include <algorithm>
#include <cstring>using namespace std;const int N = 1010, M = 20020, INF = 1e8;// 邻接表存储残留网络
// 正向边和反向边成对存在,正向边的下标异或上1得到方向边的下标
int n, m, S, T;
int h[N], e[M], f[M], ne[M], idx; // f表示容量
int q[N], d[N], pre[N];
bool st[N]; // 避免重复搜索void add(int a, int b, int c)
{// 正向边 e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx++;// 反向边,初始容量为0e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx++;
}// bfs找增广路
bool bfs()
{int hh = 0, tt = 0;memset(st, false, sizeof(st));q[0] = S, st[S] = true, d[S] = INF;while(hh <= tt) {// 从队列中弹出一个元素进行BFSint t = q[hh++];for(int i = h[t]; ~i; i = ne[i]) {// 节点t的临接边i的下一节点verint ver = e[i];// 没遍历过且边i的容量不为0if( !st[ver] && f[i] ) {st[ver] = true;// 流到节点ver的流量为流到t的流量和边i容量的最小值d[ver] = min(d[t], f[i]);// 记录节点ver前驱边的编号pre[ver] = i;if(ver == T) return true;// ver入队q[++tt] = ver;}}}return false;
}// EK 算法
int EK()
{int r = 0;while( bfs() ) {// 加上增广路的流量r += d[T];// 更新残留网络for(int i = T; i != S; i = e[pre[i] ^ 1]) {// 正向边更新f[pre[i]] -= d[T];// 反向边更新f[pre[i] ^ 1] += d[T];}}return r;
}int main()
{// 点数、边数、源点、汇点cin >> n >> m >> S >> T;// 初始化邻接表memset(h, -1, sizeof(h));while( m-- ) {int a, b, c;// 边ab的容量为ccin >> a >> b >> c;add(a, b, c);}cout << EK() << endl;return 0;
}
时间复杂度
O ( V E 2 ) O(VE^2) O(VE2)
相关文章:

图论 | 网络流的基本概念
文章目录 流网路残留网络增广路径割最大流最小割定理最大流Edmonds-Karp 算法算法步骤程序代码时间复杂度 流网路 流网络: G ( V , E ) G (V, E) G(V,E) 有向图,不考虑反向边s:源点t:汇点 c ( u , v ) c(u, v) c(u,v)ÿ…...

【音视频 | AAC】AAC音频编码详解
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...
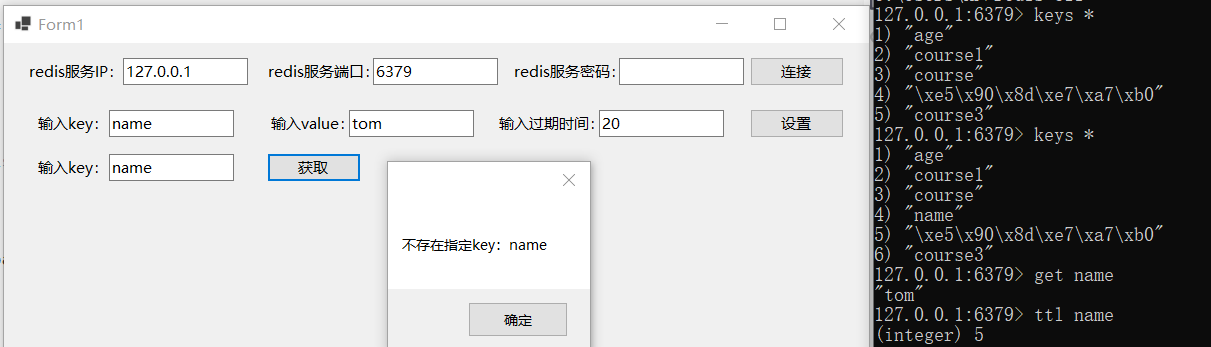
redis基本用法学习(C#调用NRedisStack操作redis)
redis官网文档中推荐C#中使用NRedisStack包连接并操作redis,本文学习C#调用NRedisStack操作redis的基本方式。 新建Winform项目,在Nuget包管理器中搜索并安装NRedisStack包,如下图所示: 主要调用StackExchange.Redis命名空间下…...

[CVPR 2023:3D Gaussian Splatting:实时的神经场渲染]
文章目录 前言小结 原文地址:https://blog.csdn.net/qq_45752541/article/details/132854115 前言 mesh 和点是最常见的3D场景表示,因为它们是显式的,非常适合于快速的基于GPU/CUDA的栅格化。相比之下,最近的神经辐射场…...
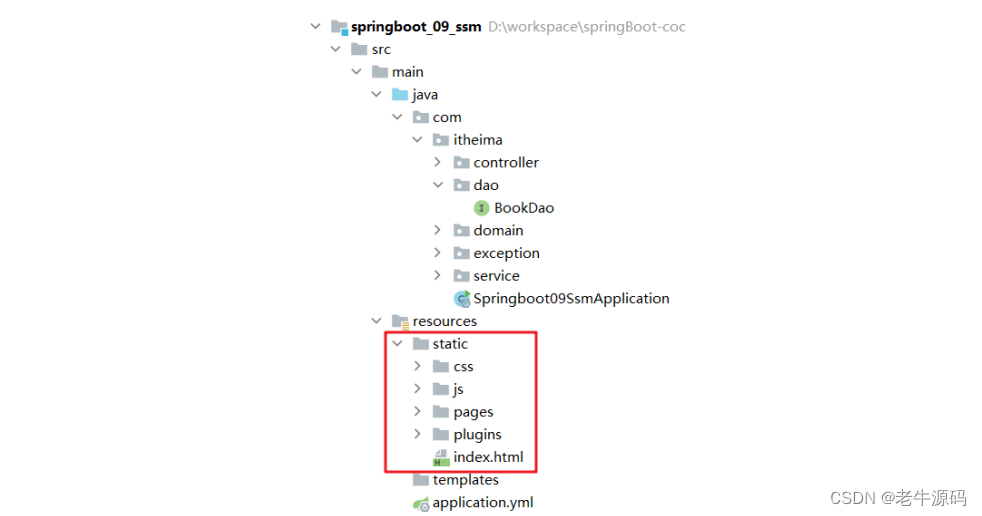
【SpringBoot快速入门】(4)SpringBoot项目案例代码示例
目录 1 创建工程3 配置文件4 静态资源 之前我们已经学习的Spring、SpringMVC、Mabatis、Maven,详细讲解了Spring、SpringMVC、Mabatis整合SSM的方案和案例,上一节我们学习了SpringBoot的开发步骤、工程构建方法以及工程的快速启动,从这一节开…...
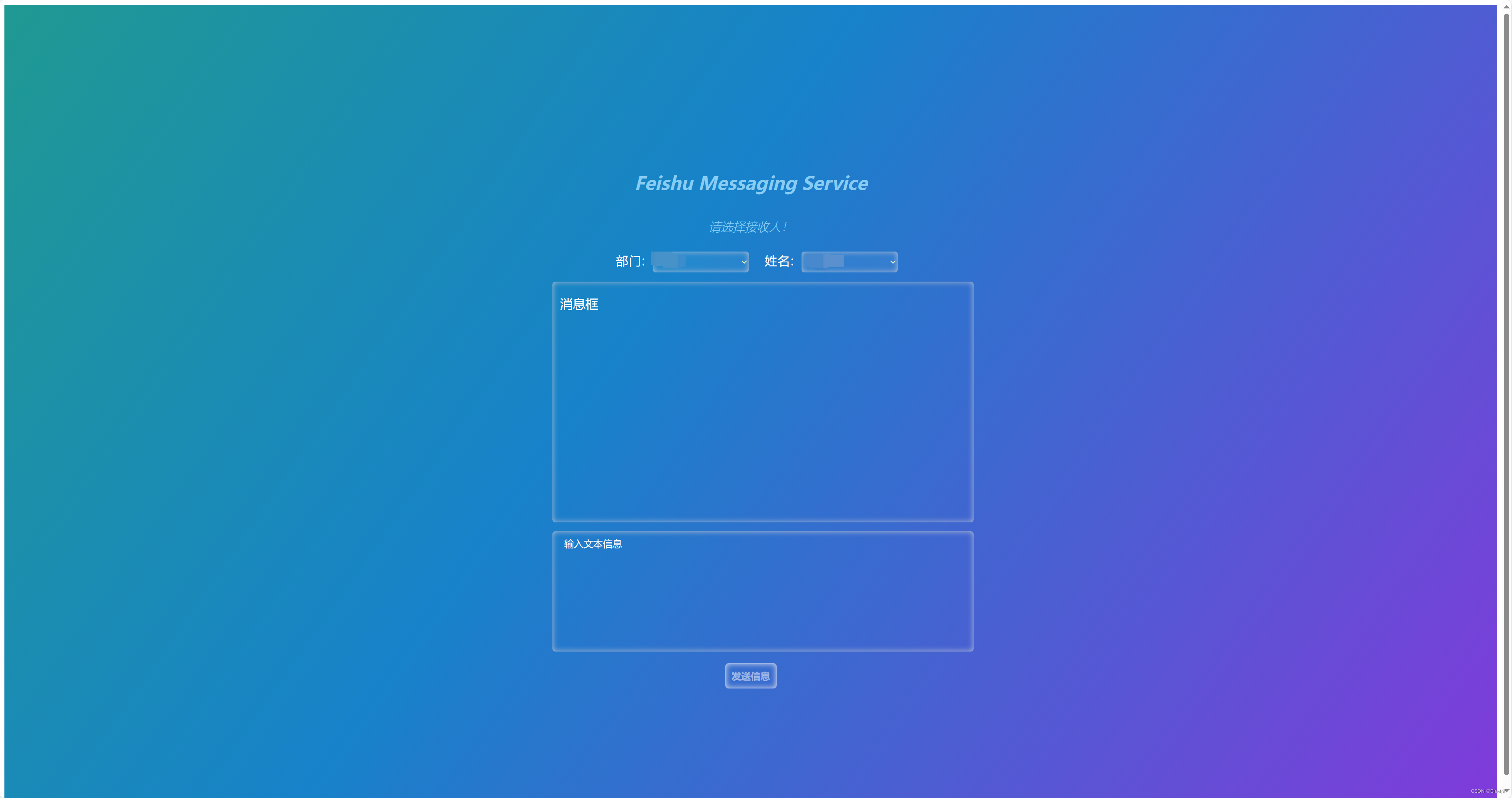
Linux服务器 部署飞书信息发送服务
项目介绍: 飞书信息发送服务是指将飞书信息发送服务部署到一个Linux服务器上。飞书是一款企业级的即时通讯和协作工具,支持发送消息给飞书的功能。通过部署飞书信息发送服务,可以方便内网发送信息给外网飞书。 项目代码结构展示: …...
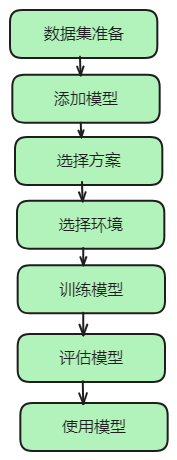
用C#也能做机器学习?
前言✨ 说到机器学习,大家可能都不陌生,但是用C#来做机器学习,可能很多人还第一次听说。其实在C#中基于ML.NET也是可以做机器学习的,这种方式比较适合.NET程序员在项目中集成机器学习模型,不太适合专门学习机器学习&a…...

Python PDF格式转PPT格式
要将PDF文件转换为PPT,我实在python3.9 环境下转成功的,python3.11不行。 需要 pip install PyMuPDF代码说话 # -*- coding: utf-8 -*-""" author: 赫凯 software: PyCharm file: xxx.py time: 2023/12/21 11:20 """im…...
搭建知识付费平台?明理信息科技为你提供全程解决方案
明理信息科技saas知识付费平台 在当今数字化时代,知识付费已经成为一种趋势,越来越多的人愿意为有价值的知识付费。然而,公共知识付费平台虽然内容丰富,但难以满足个人或企业个性化的需求和品牌打造。同时,开发和维护…...

漫谈UNIX、Linux、UNIX-Like
漫谈UNIX、Linux、UNIX-Like 使用了这么多年Redhat、Ubuntu等Linux、Windows、Solaris操作系统,你是否对UNIX、Unix-Like(类UNIX)还是不太清楚?我以前一直认为Unix-Like就等于Linux。其实,由UNIX派生出来而没有取得UN…...

Netty Review - Netty与Protostuff:打造高效的网络通信
文章目录 概念PrePomServer & ClientProtostuffUtil 解读测试小结 概念 Pre 每日一博 - Protobuf vs. Protostuff:性能、易用性和适用场景分析 Pom <dependency><groupId>com.dyuproject.protostuff</groupId><artifactId>protostuff-…...
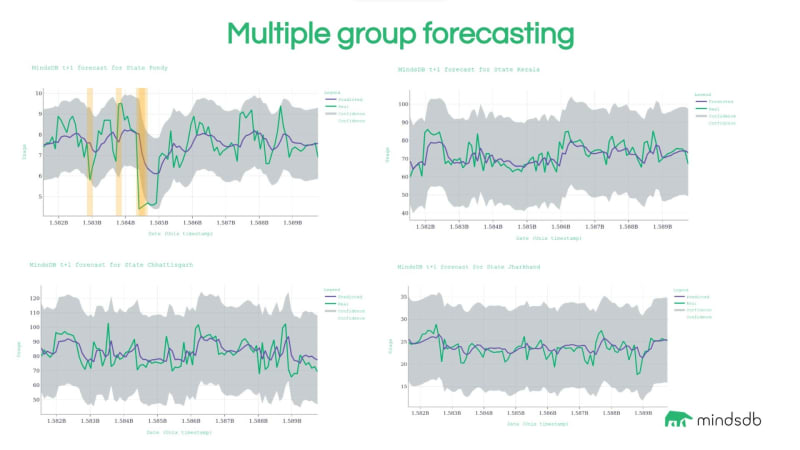
在ClickHouse数据库中启用预测功能
在这篇博文中,我们将介绍如何将机器学习支持的预测功能与 ClickHouse 数据库集成。ClickHouse 是一个快速、开源、面向列的 SQL 数据库,对于数据分析和实时分析非常有用。该项目由 ClickHouse, Inc. 维护和支持。我们将探索它在需要数据准备以…...
)
目标检测YOLO实战应用案例100讲-树上果实识别与跟踪计数(续)
目录 3.2 损失函数优化 3.3 实验过程 3.3.1 果实图像采集 3.3.2 数据扩增...
Docker 文件和卷 权限拒绝
一 创作背景 再复制Docker影像文件或访问Docker容器内已安装卷上的文件时我们常常会遇到:“权限被拒绝”的错误,在此,您将了解到为什么会出现“权限被拒绝”的错误以及如何解决这个问题。 二 目的 在深入探讨 Docker 容器中的 Permission De…...
Appium Server 启动失败常见原因及解决办法
Error: listen EADDRINUSE: address already in use 0.0.0.0:4723 如下图: 错误原因:Appium 默认的4723端口被占用 解决办法: 出现该提示,有可能是 Appium Server 已启动,关闭已经启动的 Appium Server 即可。472…...
将Abp默认事件总线改造为分布式事件总线
文章目录 原理创建分布式事件总线实现自动订阅和事件转发 使用启动Redis服务配置传递Abp默认事件传递自定义事件 项目地址 原理 本地事件总线是通过Ioc容器来实现的。 IEventBus接口定义了事件总线的基本功能,如注册事件、取消注册事件、触发事件等。 Abp.Events…...
Jupyter Notebook修改默认工作目录
1、参考修改Jupyter Notebook的默认工作目录_jupyter文件路径-CSDN博客修改配置文件 2.在上述博客内容的基础上,这里不是删除【%USERPROFILE%】而是把这个地方替换为所要设置的工作目录路径, 3.【起始位置】也可以更改为所要设置的工作目录路径&#x…...
高校/企业如何去做数据挖掘呢?
随着近年来人工智能及大数据、云计算进入爆发时期,依托三者进行的数据分析、数据挖掘服务已逐渐成为各行业进行产业升级的载体,缓慢渗透进我们的工作和生活,成为新时代升级版的智能“大案牍术”。 那么对于多数企业来说,如何做数据…...

数据仓库-数据治理小厂实践
一、简介 数据治理贯穿数仓中数据的整个生命周期,从数据的产生、加载、清洗、计算,再到数据展示、应用,每个阶段都需要对数据进行治理,像有些比较大的企业都是有自己的数据治理平台或者会开发一些便捷的平台,对于没有平…...
之 线程生命周期管理join() 与 detach())
【C++多线程编程】(五)之 线程生命周期管理join() 与 detach()
在C中,std::thread 类用于创建和管理线程。std::thread 提供了两种主要的方法来控制线程的生命周期:join 和 detach。 detach方式,启动的线程自主在后台运行,当前的代码继续往下执行,不等待新线程结束。join方式&…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...
