Unity | Shader基础知识(第八集:案例<漫反射材质球>)
目录
一、本节介绍
1 上集回顾
2 本节介绍
二、什么是漫反射材质球
三、 漫反射进化史
1 三种算法结果的区别
2 具体算法
2.1 兰伯特逐顶点算法
a.本小节使用的unity自带结构体。
b.兰伯特逐顶点算法公式
c.代码实现——兰伯特逐顶点算法
2.2 代码实现——兰伯特逐像素算法
a.像素和顶点算法的区别
b.实现代码
2.3 代码实现——半兰伯特算法
a.为什么会出现半兰伯特
b.半兰伯特公式
c.代码实现
四、下集介绍
一、本节介绍
1 上集回顾
本集讲了如何让图片和外部颜色叠加显示。
2 本节介绍
如何做一个漫反射材质球。
二、什么是漫反射材质球
1 之前的颜色材质球
我们目前只学过直接上色的材质球(如图1所示),还有上节课的颜色和图片叠加的材质球。

2 现实的光照下的球
现实光照下的大部分材质球并不是纯色且全亮的,而是(如图2所示)。

这种模拟大部分现实世界物体发光的状态,就是漫反射材质球。
备注:
反射有两种:镜面反射和漫反射。像镜子的反光,非常光滑的物体反光(比如金属),属于镜面反射,其他大部分是漫反射。具体区别详见初中物理~自己百度哦o(* ̄︶ ̄*)o
三、 漫反射进化史
我们算到最后,对屏幕来说,仅仅想知道,我这个点应该用什么颜色。
所以,对这个颜色的计算出现了三种解法。
- 兰伯特逐顶点算法
- 兰伯特逐像素算法
- 半兰伯特算法
备注:兰伯特是个人,他和别人一起研究出来了以上三个定律。
1 三种算法结果的区别
兰伯特逐顶点算法(白色和黑色交界处有些方块块的感觉、照不到的地方全黑)
兰伯特逐像素算法(白色和黑色交界处平滑过渡、照不到的地方全黑)
半兰伯特算法(白色和黑色交界处平滑过渡、照不到的地方不是全黑)
内容参考(侵权立删):
Unity Shader 漫反射(Lambert、Half Lambert) - 知乎

2 具体算法
2.1 兰伯特逐顶点算法
a.本小节使用的unity自带结构体。
struct appdata_full {float4 vertex : POSITION; //顶点坐标float4 tangent : TANGENT; //切线float3 normal : NORMAL; //法线float4 texcoord : TEXCOORD0; //第一纹理坐标float4 texcoord1 : TEXCOORD1;//第二纹理坐标float4 texcoord2 : TEXCOORD2;//第三纹理坐标float4 texcoord3 : TEXCOORD3;//第四纹理坐标fixed4 color : COLOR; //顶点颜色UNITY_VERTEX_INPUT_INSTANCE_ID //ID信息
};b.兰伯特逐顶点算法公式

公式解释:
屏幕上对应点的颜色 = (光的颜色*物体的颜色)*max(0,该点的法向量*该点的光照方向)
备注(max函数解释):
max(a,b),如果这里面a大,答案就是a
如果b大,答案就是b。
例:
max(5,20)=20
max(8,-9)=8
此处的作用:
因为颜色没有负数,如果n*l算出来小于0的时候,就直接为0,其他时候就是n*l的值。
其实就是起一个“一刀切”掉负数的作用。
得出结论:我们想计算漫反射的时候屏幕显示什么颜色,我们需要光的颜色、物体的颜色、该点的法向量(单位向量)、该点的光照方向(单位向量)。
备注:公式里的字母上带^就是单位向量的意思。
c.代码实现——兰伯特逐顶点算法
计算注意事项:
在计算n*l时,注意:该点的法向量(往往直接获取的是物体本地坐标),该点的光照方向(往往获取的是世界坐标)
这样是不能乘的,所以需要把他们都换算到一个坐标系,这里换算到世界坐标下。
会用到的方法:
UnityObjectToWorldNormal() //把物体的法线坐标,换算到世界坐标下
normalize() //把任何一个向量变成单位向量
dot() //点乘
max() //上文讲过_WorldSpaceLightPos0 //世界坐标下的光线坐标//但是要引用#include "Lighting.cginc"才能找到实现的代码:
SubShader{Pass{CGPROGRAM#pragma vertex vert#pragma fragment frag#include "UnityCG.cginc"//新的引用#include "Lighting.cginc"//返回结构体 //引用结构体appdata_full vert (appdata_full v){ //模型顶点坐标转屏幕坐标v.vertex = UnityObjectToClipPos(v.vertex);//获取法线坐标并转换成世界坐标下的法线坐标float3 worldNormal = UnityObjectToWorldNormal(v.normal);//世界坐标下的光线坐标 //单位化坐标 //获取世界坐标下的光线坐标float3 worldLight = normalize(_WorldSpaceLightPos0.xyz);//上面的公式float3 diffuse =_LightColor0.rgb * v.color.rgb * max(0,dot(worldNormal,worldLight));//算出的值给颜色v.color = float4(diffuse,1);return v;}float4 frag (appdata_full v) : SV_Target{ //输出颜色 return float4(v.color,1) ;}ENDCG}}2.2 代码实现——兰伯特逐像素算法
a.像素和顶点算法的区别
- 从写法角度来看,顶点算法是在顶点着色器中写的,像素算法是在片元着色器中写的。
- 从原理角度来说,因为顶点是初始值,经过一系列计算后,数据就会和我们想要的有些偏差。
例:让你拿笔写一个字,你可能就写了,但是让你拿竹竿上面绑个中性笔写字,你就写不准了,肯定是离画出来的地方越近,画出来越是自己想要的。
结论:像素着色器离最后的显示比较近,所以出来的结果和我们想要的更一致。
b.实现代码
Shader "Unlit/005_1"
{SubShader{Pass{CGPROGRAM#pragma vertex vert#pragma fragment frag#include "UnityCG.cginc"#include "Lighting.cginc"appdata_full vert (appdata_full v){ v.vertex = UnityObjectToClipPos(v.vertex);//把法线转换成世界坐标,传进去v.normal = UnityObjectToWorldNormal(v.normal);return v;}float4 frag (appdata_full v) : SV_Target{//法线世界坐标float3 worldNormal = v.normal;//光线世界坐标float3 worldLight = normalize(_WorldSpaceLightPos0.xyz);//计算颜色float3 diffuse =_LightColor0.rgb * v.color.rgb * max(0,dot(worldNormal,worldLight));//把颜色传进去return float4(diffuse,1) ;}ENDCG}}
}
2.3 代码实现——半兰伯特算法
a.为什么会出现半兰伯特
兰伯特的两个算法,得到的球,在没有光线照射的时候都是黑色的,但玩游戏的时候往往希望,虽然光线无法照到,但我们可以看见。
数学知识:公式中的n*l值的范围是【-1,1】之间,我们希望把这个区间改成【0,1】(前面的课学过),【-1,1】*0.5+0.5,就可以转成【0,1】,0的时候就是之前光照模型中黑色部分,越靠近1越亮。
因为我们实际上并不是需要它看不见,只是需要它要明暗变化,所以我们在环境光的基础上加上兰伯特公式计算出的值,就有了明暗变化。
于是就出现了第三种,半兰伯特。
b.半兰伯特公式
在上图基础上:
最终颜色 = 环境光+Cdiffuse
c.代码实现
这里其他代码都没有变,只更改了上图0.5的部分。最后输出前,再加入环境光。
备注:
获取环境光强度的方法:UNITY_LIGHTMODEL_AMBIENT.xyz
Shader "Unlit/005_2"
{SubShader{Pass{CGPROGRAM#pragma vertex vert#pragma fragment frag#include "UnityCG.cginc"#include "Lighting.cginc"appdata_full vert (appdata_full v){v.vertex = UnityObjectToClipPos(v.vertex);v.normal = UnityObjectToWorldNormal(v.normal);return v;}float4 frag (appdata_full v) : SV_Target{float3 worldNormal = v.normal;float3 worldLight = normalize(_WorldSpaceLightPos0.xyz);//本节变动//获取环境光float3 anbient = UNITY_LIGHTMODEL_AMBIENT.xyz;//计算范围float halfLamient = dot(worldNormal,worldLight)*0.5+0.5;//计算反射强度float3 diffuse =_LightColor0.rgb * v.color.rgb *halfLamient;//反射光加光照强度float3 c = anbient + diffuse;return float4(c,1) ;}ENDCG}}
}四、下集介绍
本集讲了3种计算反射光的方法。
下集讲光照计算,高光反射。(最晚更新日期,1月7日)
相关文章:

Unity | Shader基础知识(第八集:案例<漫反射材质球>)
目录 一、本节介绍 1 上集回顾 2 本节介绍 二、什么是漫反射材质球 三、 漫反射进化史 1 三种算法结果的区别 2 具体算法 2.1 兰伯特逐顶点算法 a.本小节使用的unity自带结构体。 b.兰伯特逐顶点算法公式 c.代码实现——兰伯特逐顶点算法 2.2 代码实现——兰伯特逐…...
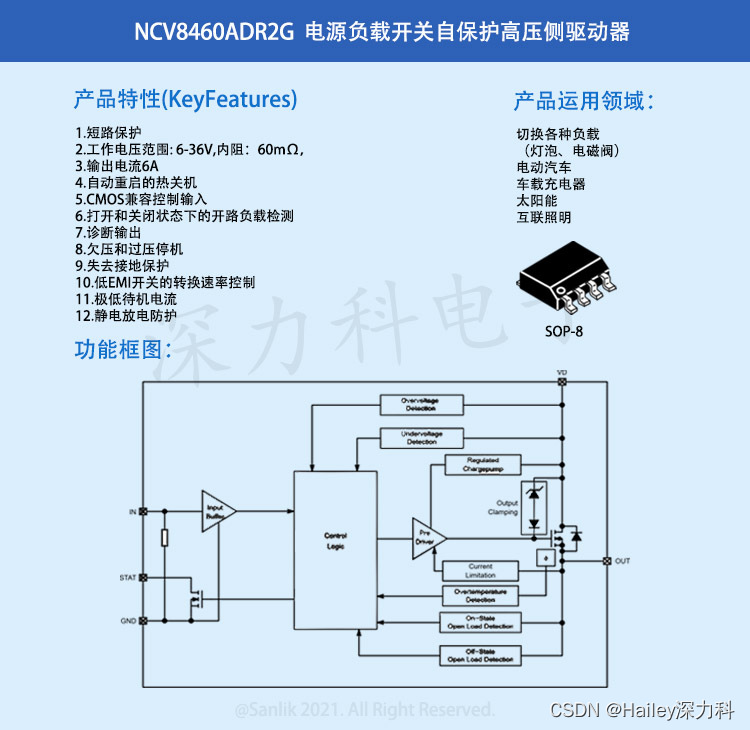
NCV8460ADR2G在汽车和工业应用中高压侧驱动如何破?
NCV8460ADR2G是一款完全保护的高压侧驱动器,可用于开关各种负载,如灯泡、电磁阀和其他致动器。该器件可以通过有源电流限制和高温关断针对过载情况进行内部保护。 诊断状态输出引脚提供了高温以及开关状态开路负载情况的数字故障指示。 特性:…...

在打日志时,如何使用snowflake-id快速方便得随机获取query的唯一id
步骤一:安装snowflake-id pip install snowflake-id步骤二:代码示例 from snowflake import SnowflakeGeneratorgen SnowflakeGenerator(42)for i in range(100):val next(gen)print(val)参考文档: https://pypi.org/project/snowflake-…...
Linux之yum管理器
目录 yum管理器 yum相关指令 yum list yum list | grep yum install yum remove 拓展 1.yum install -y man-pages 2.切换yum源 3.yum install -y epel-release 4. yum install -y lrzsz rz指令 sz指令 在window系统上,我们会在电脑自带的应用商…...

ubuntu 搭建本地私有pip源
# 搭建本地私有pip源 pip install pip2pi# 创建目录 mkdir /data/work/PyPip/ mkdir /data/work/PyPip/packages cd /data/work/PyPip/# 创建需要从外网源同步的package touch requirements_roop.txt# 批量同步 pip2tgz /data/work/PyPip/packages -r requirements_roop.txt# 同…...
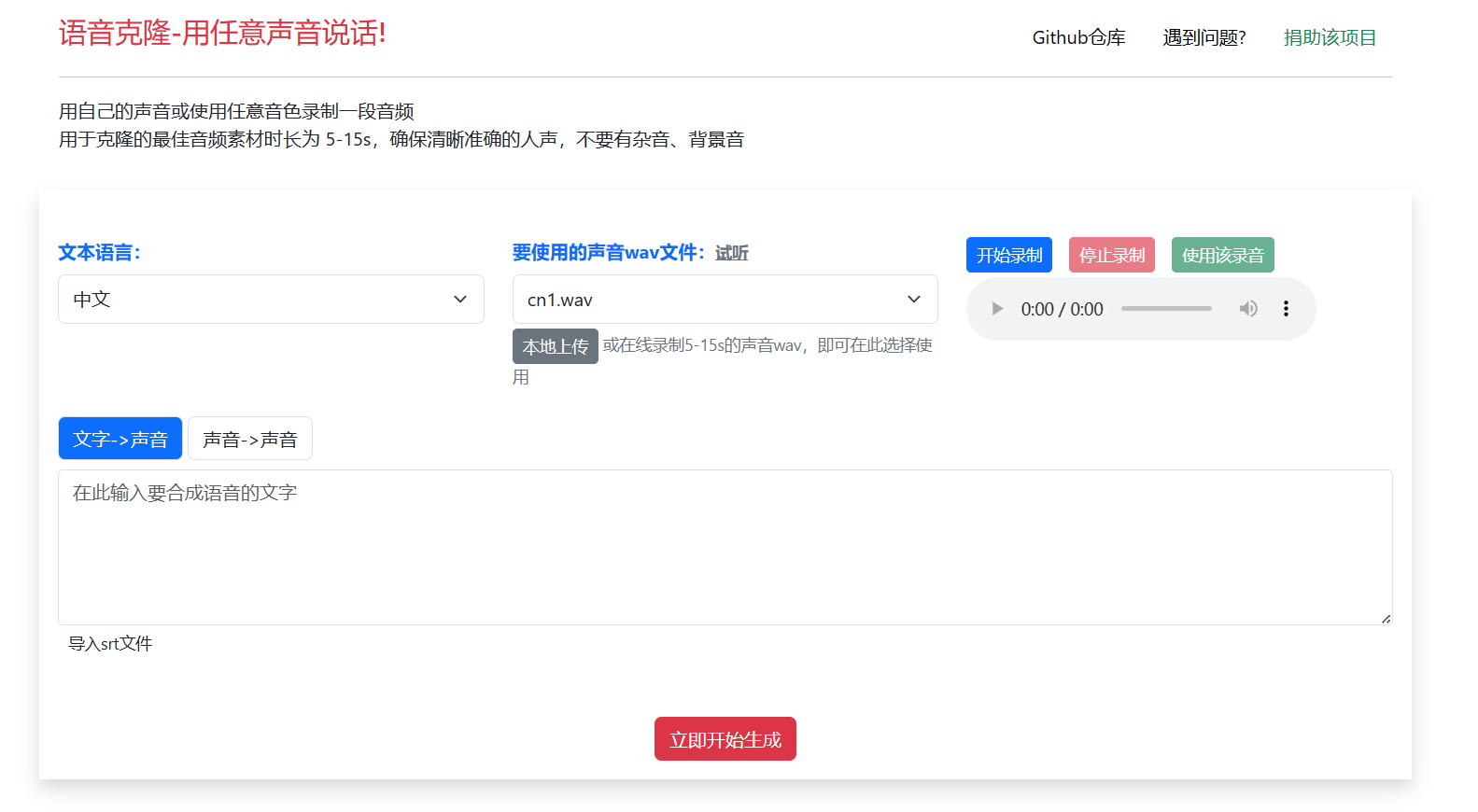
声音克隆:让你的声音变得无所不能
什么是声音克隆? 声音克隆是一种利用人工智能技术,根据一段声音样本,生成与之相似或完全相同的声音的过程。声音克隆可以用于多种场景。 声音克隆的原理是利用深度学习模型,从声音样本中提取声音特征,然后根据目标文…...

hadoop02_HDFS的API操作
HDFS的API操作 1 HDFS 核心类简介 Configuration类:处理HDFS配置的核心类。 FileSystem类:处理HDFS文件相关操作的核心类,包括对文件夹或文件的创建,删除,查看状态,复制,从本地挪动到HDFS文件系统中等。…...
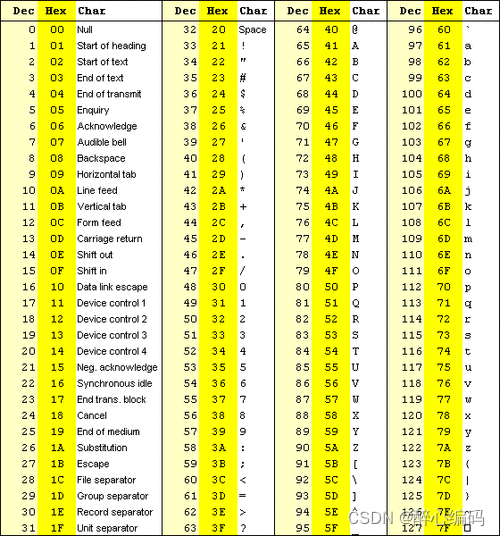
使用C语言将ASCII明文编码为GSM短信体格式
一、背景介绍 GSM(Global System for Mobile Communications)是全球移动通信系统的简称,而GSM 03.38是GSM系统中用于短信编码的标准。GSM 03.38字符集采用7-bit编码,与ASCII的8-bit编码有所不同。为了将ASCII编码的文本转换为GSM…...
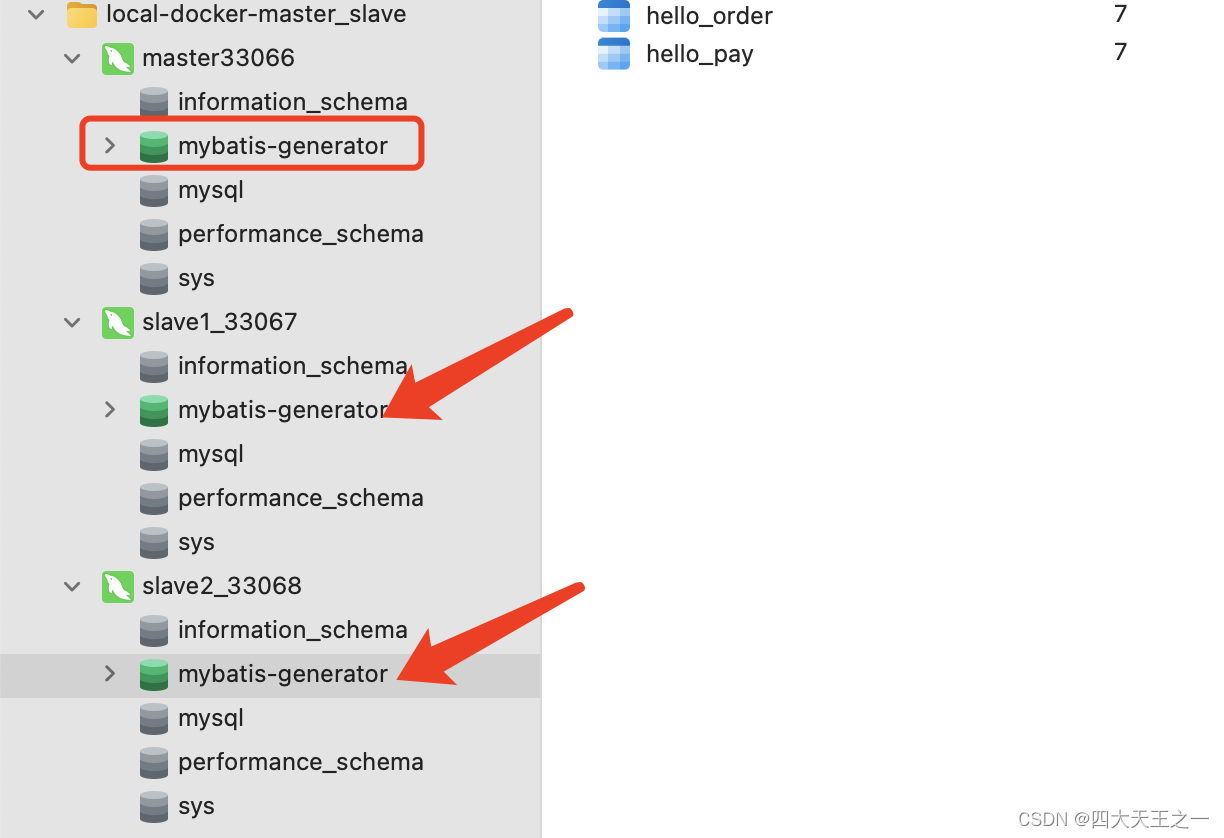
docker搭建mysql8.0.32,实现主从复制(一主两从)
安装docker的步骤、使用命令就不写了,本文章是基于会使用docker、linux基本命令的基础上来写的。 开始步骤: 1. 拉取 mysql 镜像 docker pull mysql:8.0.32 2. 启动容器并运行mysql a. 准备mysql的配置文件(该配置文件是:mysq…...

AOP springboot
1. 2. Around(“execution(* com.example.demo.controller..(…))”) 代表所有的类下面所有的方法任意参数 3....

Python Flask 基础入门第六课: Flask 全局变量 current_app, g 以及 session各自如何使用 有什么差异
全局变量 current_app, g 以及 session 全局变量差异汇总表current_app章节1 current_app - 当前应用实例current_app的基本概念current_app的作用current_app的使用 章节2:current_app的上下文什么是应用上下文?current_app与应用上下文的关系current_a…...

第33节: Vue3 方法与在线检测
UniApp 使用 Vue3 框架时,您可以使用方法和在线检测来处理应用程序中的逻辑和数据。下面是一个示例,演示了如何在 UniApp 中使用 Vue3 框架使用方法和在线检测: <template> <view> <button click"handleClick"&g…...

React学习计划-React16--React基础(二)组件与组件的3大核心属性state、props、ref和事件处理
1. 组件 函数式组件(适用于【简单组件】的定义) 示例: 执行了ReactDOM.render(<MyComponent/>, ...)之后执行了什么? React解析组件标签,找到了MyComponent组件发现组件是使用函数定义的,随后调用该…...

flink yarn-session 启动失败retrying connect to server 0.0.0.0/0.0.0.0:8032
原因分析,启动yarn-session.sh,会向resourcemanager的端口8032发起请求: 但是一直无法请求到8032端口,触发重试机制会不断尝试 备注:此问题出现时,我的环境ambari部署的HA 高可用hadoop,三个节点…...
)
.NET面试题(二)
1.c# 中new关键字的作用 实例化对象和调用构造函数:当使用 new 关键字创建一个类的实例时,它会为对象分配内存,并调用相应的构造函数来初始化该对象。 隐藏基类成员(方法、属性、事件等):当在派生类中…...

ffplay工具
在编译ffmpeg时,如果系统中包含了SDL库,则会默认编译生成ffplay工具,否则无法生成ffplay工具。 ffplay即可以作为播放器,也可以作为很多图像化音视频数据的分析工具,通过它可以看到视频图像的运动估计方向、音频数据的…...

第36节: Vue3 事件修饰符
在UniApp中使用Vue3框架时,你可以使用事件修饰符来更方便地处理用户交互事件。以下是一个示例,演示了如何在UniApp中使用Vue3框架使用事件修饰符: <template> <view> <button click.prevent"handleClick">Cli…...
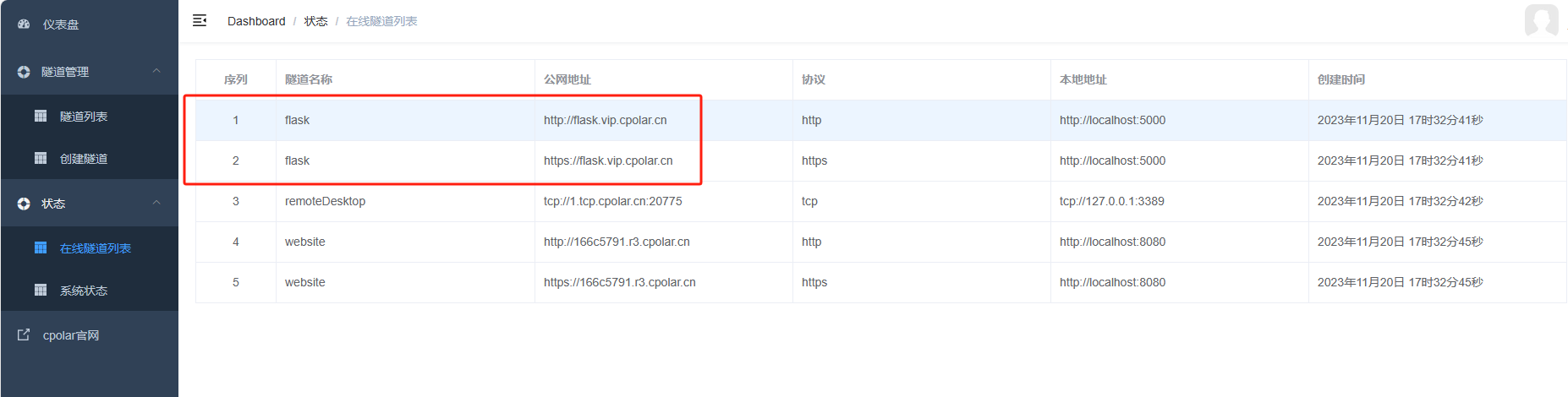
如何在本地安装Flask并将其web界面发布到公网上远程访问协同开发
目录 前言 1. 安装部署Flask 2. 安装Cpolar内网穿透 3. 配置Flask的web界面公网访问地址 4. 公网远程访问Flask的web界面 前言 本篇文章讲解如何在本地安装Flask,以及如何将其web界面发布到公网上并进行远程访问。 Flask是目前十分流行的web框架,…...
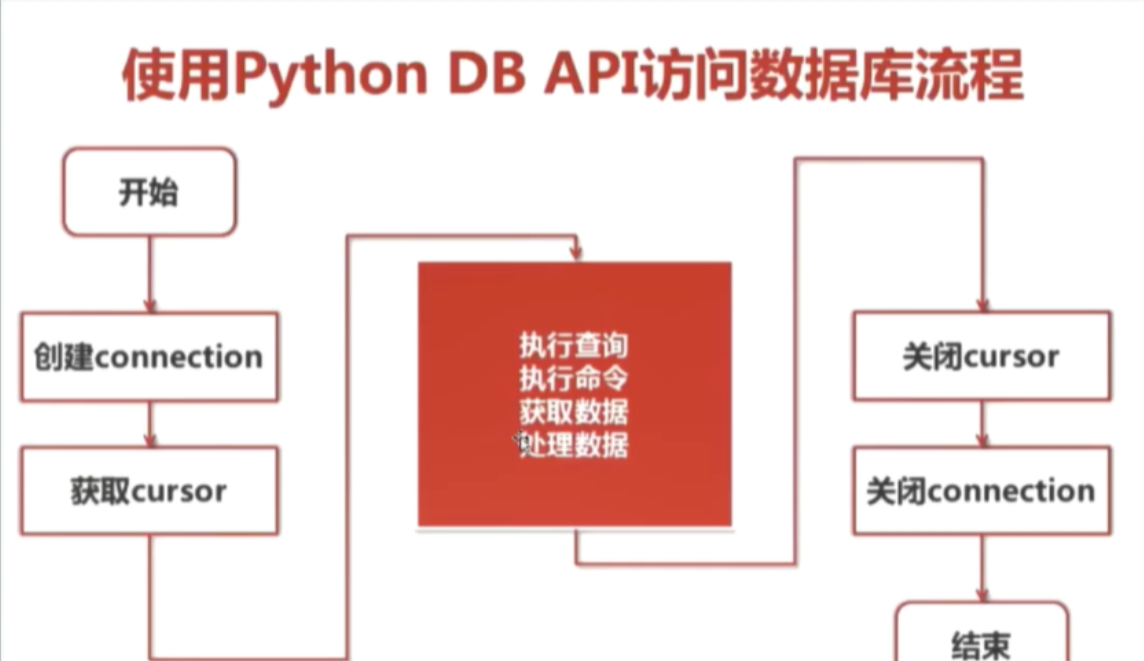
八:爬虫-MySQL基础
一:MySQL数据库基础 1.MySQL数据库介绍 MySQL是一个[关系型数据库管理系统],由瑞典MySQL AB 公司开发,属于 Oracle 旗下产品。MySQL 是最流行的关系型数据库管理系统之一,在 WEB 应用方面,MySQL是最好的 RDBMS (Rela…...
Android定制ROM简介
Android定制ROM简介 这篇文章是为对自定义ROM、AOSP等词汇不太熟悉的技术爱好者和好奇的人写的。我希望通过向您介绍这个世界来开始博客写作。 在我们将注意力转向定制ROM之前,让我们先了解一些基础知识。 什么是操作系统? 维基百科对此的定义简洁而…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...
