【全网首发】洛谷P1020 [NOIP1999 提高组] 导弹拦截
P1020 导弹拦截 の 题目传送门。
解题思路
显然,第一问求的是最长不上升子序列。
于是接下来直接抛开第一问不谈,也不考虑优化,直接考虑第二问。待会就知道原因了。
引理:Dilworth 定理
狄尔沃斯定理亦称偏序集分解定理,该定理断言:对于任意有限偏序集,其最大反链中元素的数目必等于最小链划分中链的数目。此定理的对偶形式亦真,它断言:对于任意有限偏序集,其最长链中元素的数目必等于其最小反链划分中反链的数目。
该定理在该问题上可以理解成:把序列分成不上升子序列的最少个数,等于序列的最长上升子序列长度。把序列分成不降子序列的最少个数,等于序列的最长下降子序列长度。
则第二问等价于最长上升子序列。
贪心
先不管引理对我们有什么用,我们直接思考第二问贪心怎么做。
对于每个数,既可以把它接到已有的导弹拦截后面,也可以建立一个新系统。要使子序列数最少,应尽量不建立新序列。
另外,应让每个导弹系统的末尾尽可能大,这样能接的数更多。因为一个数若能接到小数后面,必然能接到大数后面,反之则不成立。根据这些想法,可总结出如下贪心流程:
从前往后扫描每个数,对于当前数
1.若现有子序列的结尾都小于它,则创建新子序列。
2.否则,将它放到结尾大于等于它的最小数后
贪心证明
我们可以知道,证明 A=B,可证 A≤B 且 A≥B。
记 A 为贪心解,B 为最优解。
贪心解能覆盖所有数,且形成的都是不升序列,因此合法。由定义,B≤A。
假设最优解对应的方案和贪心方案不同,从前往后找到第一个不在同一序列的数 x。假设贪心解中 x 前面的数是 a,最优解中 x 前面的数是 b,a 后面的数是 y,由于贪心会让当前数接到大于等于它的最小数后面,所以 ,x,y≤a≤b。
此时,在最优解中,把 x 一直到序列末尾,和 y 一直到序列末尾交换位置,这样做不影响正确性,也不增加序列个数,但会使 x 在最优解和贪心解中所处的位置相同。由于序列中的数是有限的,只要一直做下去,一定能使最优解变为贪心解。因此A≤B。
等等,第二问根据引理是求最长上升子序列,但是贪心也可以求。说明我们的贪心解法等于最长上升子序列 !!(引理作用即在此处)
贪心可以求上升子序列,自然连第一问求的最长不上升子序列也可以求了。
最坏复杂度O(n2),但是数据很水,可以完美通过此题。
我们也可以对此代码进行二分优化(即查找 k 的时候):
AC 代码:
#include<bits/stdc++.h>
#define up(l,r,i) for(int i=l,END##i=r;i<=END##i;++i)
#define dn(r,l,i) for(int i=r,END##i=l;i>=END##i;--i)
using namespace std;
typedef long long i64;
const int INF =2147483647;
const int MAXN=1e5+3;
int n,t,H[MAXN],F[MAXN];
int main(){while(~scanf("%d",&H[++n])); --n;t=0,memset(F,0,sizeof(F)),F[0]=INF;up(1,n,i){int l=0,r=t+1; while(r-l>1){int m=l+(r-l)/2;if(F[m]>=H[i]) l=m; else r=m;}int x=l+1; // dp[i]if(x>t) t=x; F[x]=H[i];}printf("%d\n",t);t=0,memset(F,0,sizeof(F)),F[0]=0;up(1,n,i){int l=0,r=t+1; while(r-l>1){int m=l+(r-l)/2;if(F[m]<H[i]) l=m; else r=m;}int x=l+1;if(x>t) t=x; F[x]=H[i];}printf("%d\n",t);return 0;
}相关文章:

【全网首发】洛谷P1020 [NOIP1999 提高组] 导弹拦截
P1020 导弹拦截 の 题目传送门。 解题思路 显然,第一问求的是最长不上升子序列。 于是接下来直接抛开第一问不谈,也不考虑优化,直接考虑第二问。待会就知道原因了。 引理:Dilworth 定理 狄尔沃斯定理亦称偏序集分解定理&#…...
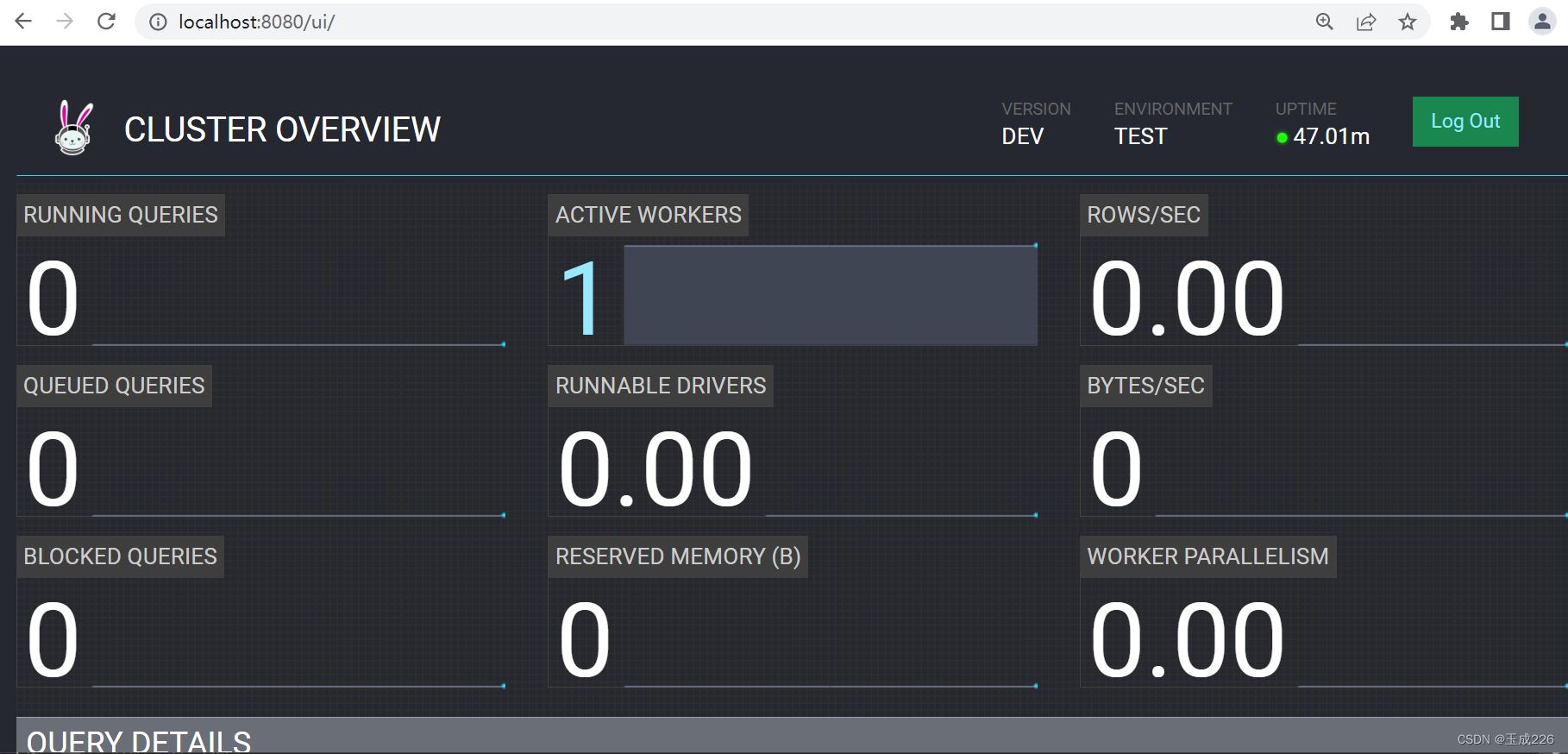
trino-435版本windows下源码编译
一、源码下载地址 https://github.com/trinodb/trino/tags 二、编译环境及工具准备 1、maven (1)版本:3.6.3 (2)settings.xml配置 <?xml version"1.0" encoding"UTF-8"?> <settin…...

java类和对象的思想概述
0.面向对象Object OOP——名人名言:类是写出来的,对象是new出来的 **> 学习面向对象的三条路线 java类以及类成员:(重点)类成员——属性、方法、构造器、(熟悉)代码块、内部类面向对象特征&…...

ant design vue3中引入message消息提示,全局引入亲测有效
两种方式 第一种:使用provide和inject方式 第二种:使用全局挂载$message方式 第一种: //main.ts import { createApp } from vue; import App from ./App; import Antd,{ message } from ant-design-vue; import ant-design-vue/es/mess…...
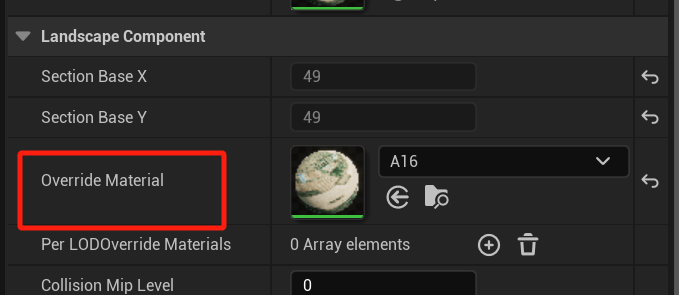
UE5 Landscape 制作GIS卫星图地形
1. 总体想法: 制作GIS地形,使用Landscaping MapBox是一个好方法,但是区域过大,会占用很多内存 https://blog.csdn.net/qq_17523181/article/details/135029614 如果采用QGis,导出卫星图,在UE5里拼合出地形…...

opencv入门到精通——改变颜色空间
目录 目标 改变颜色空间 对象追踪 如何找到要追踪的HSV值? 目标 在本教程中,你将学习如何将图像从一个色彩空间转换到另一个,像BGR↔灰色,BGR↔HSV等 除此之外,我们还将创建一个应用程序,以提取视频中的…...
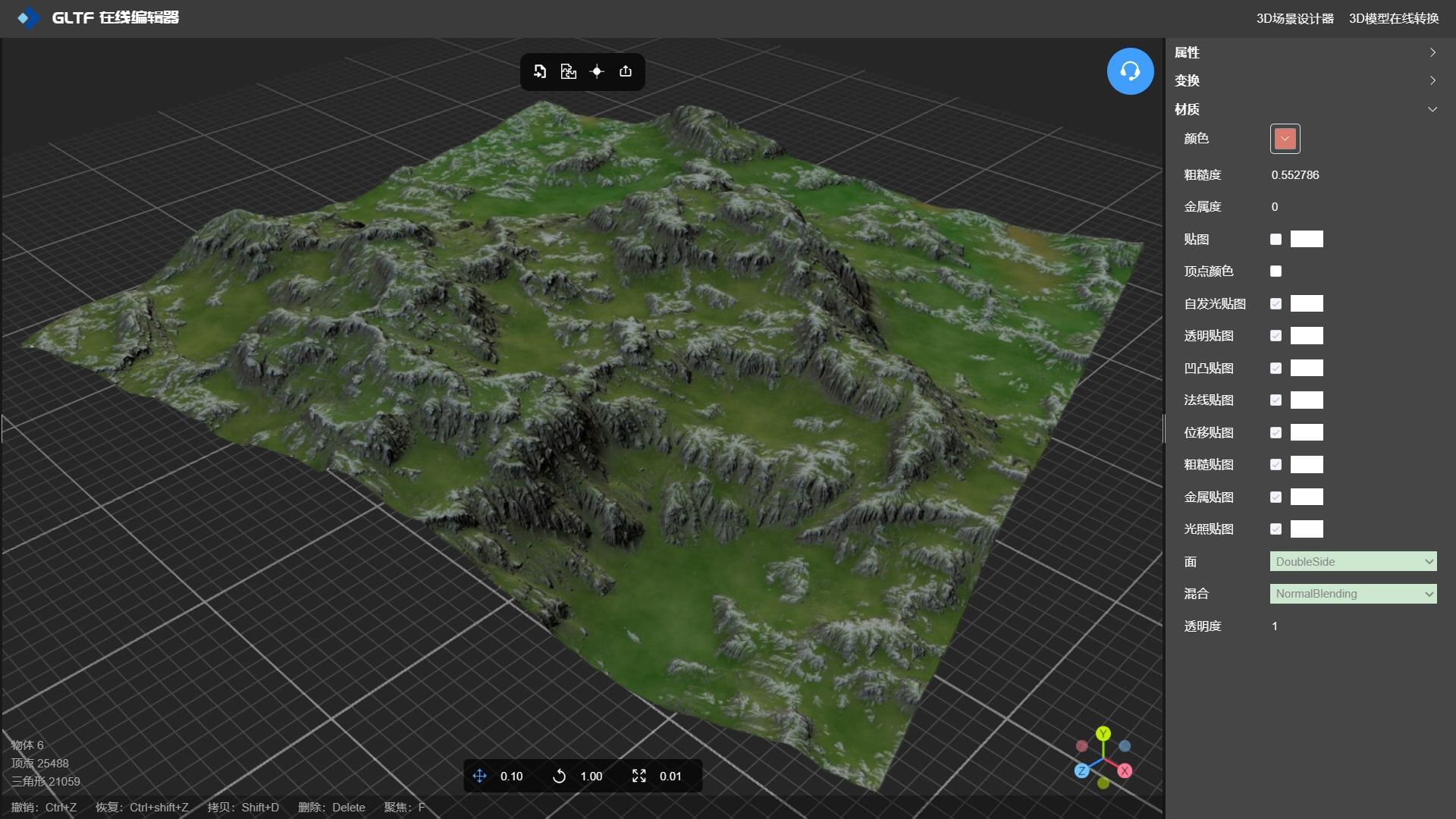
法线贴图实现地形模型皱褶、凹凸不平的纹理效果
在线工具推荐: 3D数字孪生场景编辑器 - GLTF/GLB材质纹理编辑器 - 3D模型在线转换 - Three.js AI自动纹理开发包 - YOLO 虚幻合成数据生成器 - 三维模型预览图生成器 - 3D模型语义搜索引擎 法线贴图在3D建模中扮演着重要的角色,它通过模拟表面的微…...

【SpringBoot篇】基于Redis实现生成全局唯一ID的方法
文章目录 🍔生成全局唯一ID🌹为什么要生成全局唯一id🌺生成全局id的方法✨代码实现 🍔生成全局唯一ID 是一种在分布式系统下用来生成全局唯一id的工具 在项目中生成全局唯一ID有很多好处,其中包括: 数据…...

轻度听力损失的儿童需要早期干预吗?
一些宝宝在做听力筛查时总是不通过,进一步听力诊断发现宝宝有轻度的听力损失,刚知道这个消息时,家长可担心了,总想着宝宝是不是听不到啊?但是一段时间后,有些家长又会忽略宝宝的听力问题,因为部…...

【Spring Security】认证密码加密Token令牌CSRF的使用详解
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《Spring Security》。🎯🎯 …...

python一点通: 一文讲清Post 和 Put操作区别!
当我们使用网络服务时,如果我们不能小心地区分 POST 和 PUT,有时可能会触发错误。 在 Web 开发世界中,特别是在处理 RESTful API 时,HTTP 方法 POST 和 PUT 经常被使用,但常常被误解。这两者都用于向服务器发送数据&a…...
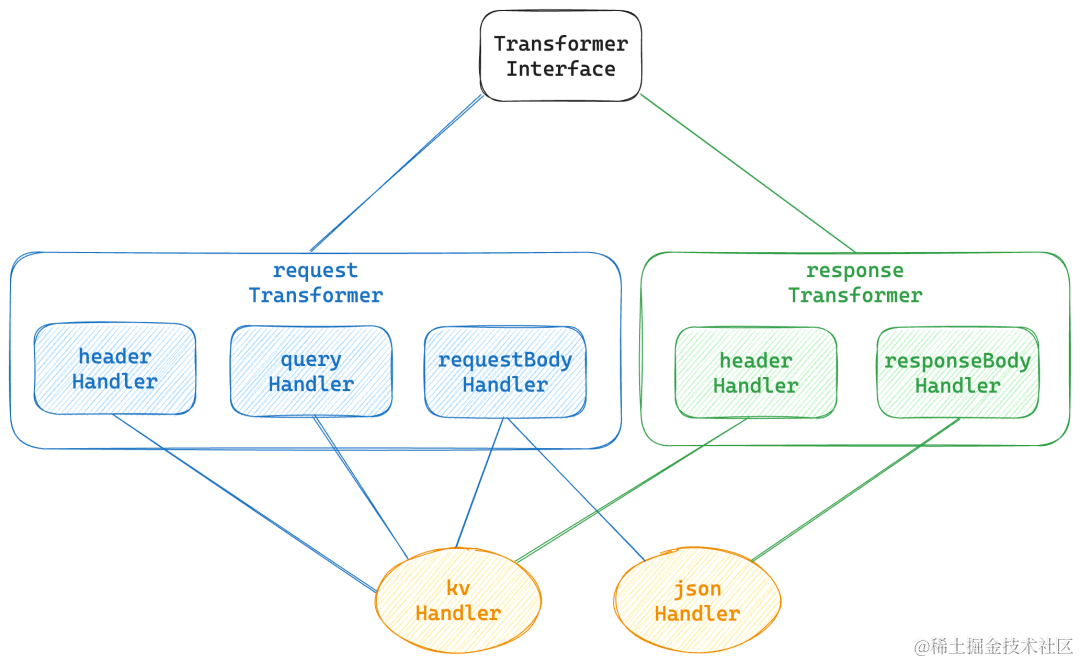
通过 Higress Wasm 插件 3 倍性能实现 Spring-cloud-gateway 功能
作者:韦鑫,Higress Committer,来自南京航空航天大学分布式系统实验室 导读:本文将和大家一同回顾 Spring Cloud Gateway 是如何满足 HTTP 请求/响应转换需求场景的,并为大家介绍在这种场景下使用 Higress 云原生网关的…...
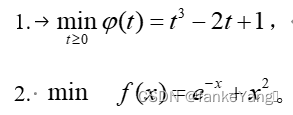
0.618算法和基于Armijo准则的线搜索回退法
0.618代码如下: import math # 定义函数h(t) t^3 - 2t 1 def h(t): return t**3 - 2*t 1 # 0.618算法 def golden_section_search(a, b, epsilon): ratio 0.618 while (b - a) > epsilon: x1 b - ratio * (b - a) x2 a ratio * (b - a) h_…...
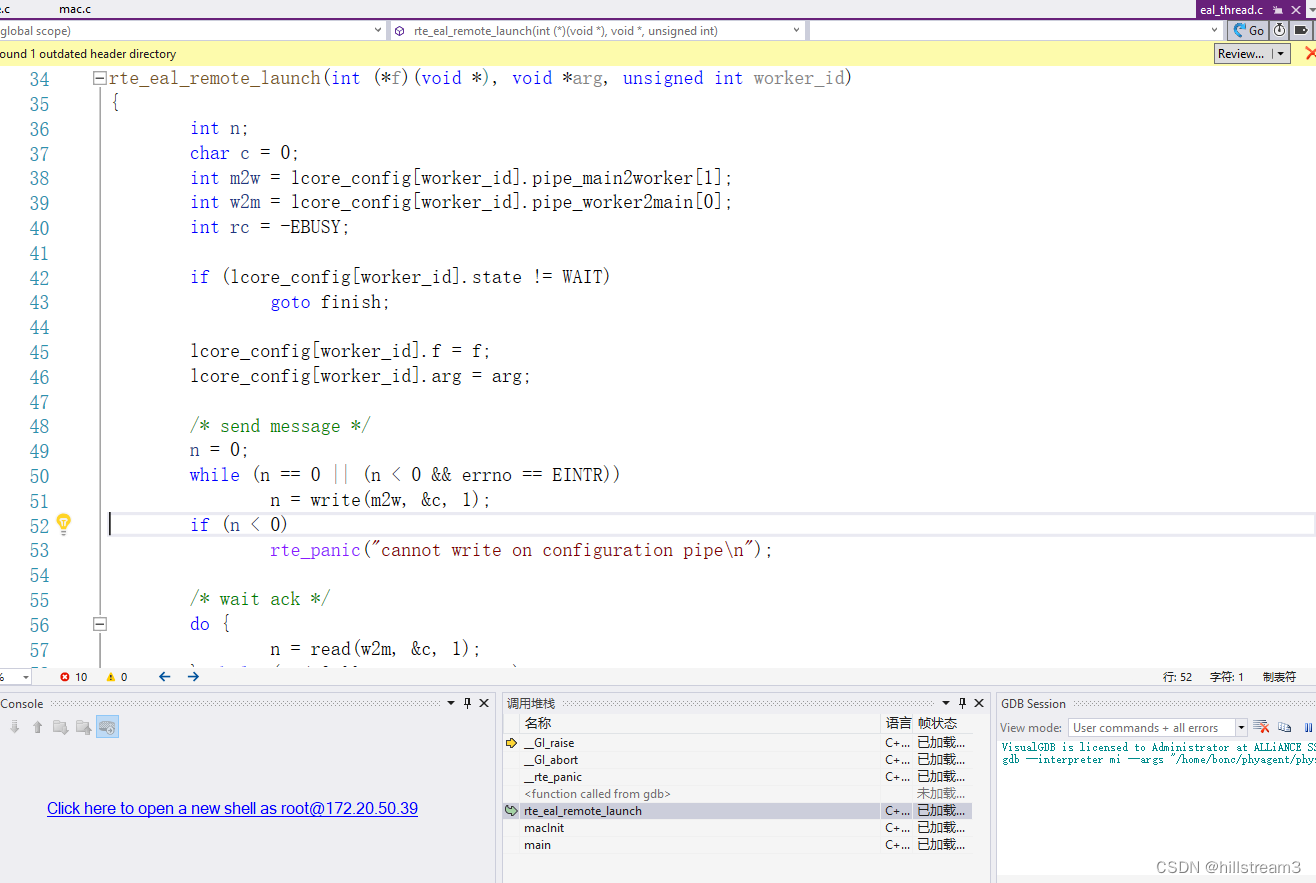
DPDK单步跟踪(3)-项目配置和单步跟踪
项目配置 下面都是示例的情况,请大家根据自己的工程来修改 ## 首先是配置CMake build setting Debug setting 这里最重要的是: –proc-type secondary 表示这是以secondary模式启动的dpdk客户端。 ## path mapping 然后根据自己的需要,配置…...

.NET core 自定义过滤器 Filter 实现webapi RestFul 统一接口数据返回格式
之前写过使用自定义返回类的方式来统一接口数据返回格式,.Net Core webapi RestFul 统一接口数据返回格式-CSDN博客 但是这存在一个问题,不是所有接口会按照定义的数据格式返回,除非每个接口都返回我们自定义的类,这种实现起来不…...

vue3 使用addRoute动态添加路由,页面刷新就白屏解决办法
问题,通过接口动态添加路由,第一次从登录页跳转还是正常的,说明路由添加成功了,但是刷新后就白屏了,且控制台报错路由匹配不到,在项目的main.js,router和路由拦截器中添加了一大堆打印后发现&am…...

探索鸿蒙:了解华为鸿蒙操作系统的基础课程
目录 学习目标: 学习内容: 学习时间: 学习产出: 介绍鸿蒙操作系统的起源和发展历程。 理解鸿蒙操作系统的核心概念和体系结构。 学习如何搭建和配置鸿蒙开发环境。 掌握基础的鸿蒙应用开发技术,包括应用的创建、…...
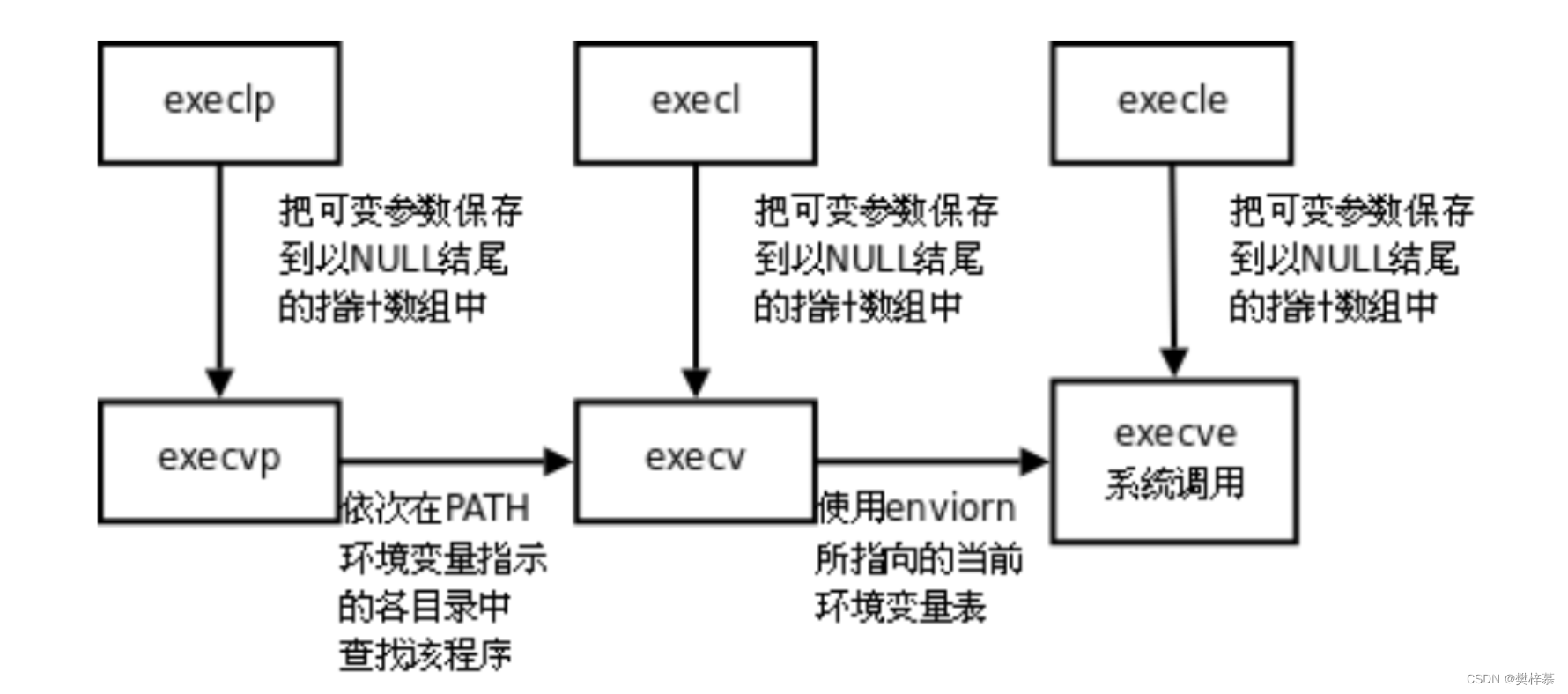
【Linux】进程周边007之进程控制
👀樊梓慕:个人主页 🎥个人专栏:《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》《C》《Linux》 🌝每一个不曾起舞的日子,都是对生命的辜负 目录 前言 1.进程创建 2.进程终止 2.…...

【C++】vector容器的模拟实现
目录 一,框架设计 二,构造函数 三,析构函数 四,赋值运算符 五,容器接口的实现 1,迭代器实现 2,“ [] ”运算符的实现 3,swap交换和resize重设大小 4,insert插入…...
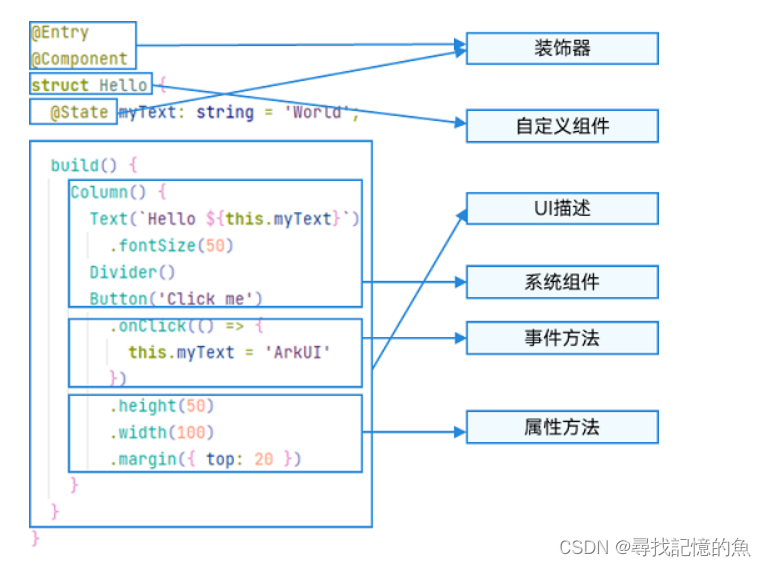
华为Harmony——ArkTs语言
文章目录 一、简单示例二、声明式UI描述创建组件无参有参数 配置属性配置事件配置子组件 三、自定义组件基本用法基本结构成员函数/变量 一、简单示例 我们以一个具体的示例来说明ArkTS的基本组成。如下图所示,当开发者点击按钮时,文本内容从“Hello Wo…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
