数据结构考研习题精选
1

A假设比较t次,由于换或不换,则必然有2^t种可能。又设有n个关键字,n!排列组合,则必然有2^t>=n!,带入n即可解出。
2

注意这里没有考虑于哨兵的比较,少了一次,所以按n*(n-1)/2可以解出比较次数是10,B
3

注意这里增量为4要比较完整,A
4

比较次数变成了nlog2n但是移动次数没有改变,还是n^2,所以时间复杂度还是O(n^2)
5

二分的越均匀速度越快,越有序速度越慢,所以A、D
6

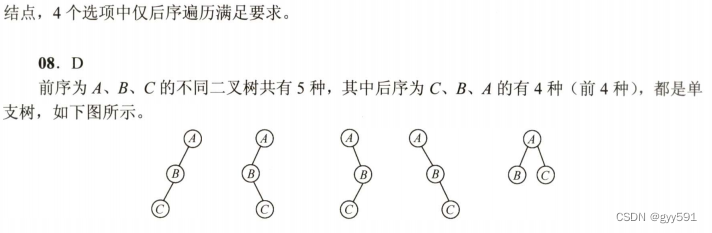
从小到大排{11,18,23,68,69,73,93},从大到小排{93,73,69,68,23,18,11},要求最终位置元素可以作为枢纽,只有3、4可以,C
7


每趟都要确定至少1个最终位置的结果,D只有1个32满足

8


int kth_elem(int low,int high,int k){int pivot=num[low];int low_t=low;int high_t=high;while(low<high){while(low<high && pivot<=num[high]) high--;num[low]=num[high];while(low<high && pivot>=num[low]) low++;num[high]=num[low];}num[low]=pivot;if(low==k){return num[low];}else if(low<k){return kth_elem(low+1,high_t,k);}else if(low>k){return kth_elem(low_t,low-1,k);}
}void flag(int a[],int n){int i=0,j=0,k=n-1;while(j<=k){switch(a[j]){case red:swap(a[i],a[j]);i++,j++;break;case white:j++;break;case blue:swap(a[j],a[k]);k--;}}cout<<i<<' '<<k<<endl;for(int m=0;m<n;m++){if(m<i) cout<<red<<' ';else if(i<=m && m<=k) cout<<white<<' ';else{cout<<blue<<' ';}}
}int best_meet(int n){int low=0,high=n-1; int low_t=low;int high_t=high;int k=n/2;bool flag=false;while(!flag){int pivot=num[low];while(low<high){while(low<high && pivot<=num[high]) high--;num[low]=num[high];while(low<high && pivot>=num[low]) low++;num[high]=num[low]; }num[low]=pivot;if(low==k-1){flag=true;}else if(low<k){low_t=++low;high=high_t;}else if(low>k){low=low_t;high_t=--high;} }int s1=0,s2=0;for(int i=0;i<k;i++) s1+=num[i];for(int i=k;i<n;i++) s2+=num[i];return s2-s1;
}
10



11


17B,注意是逐个插入,随时调整
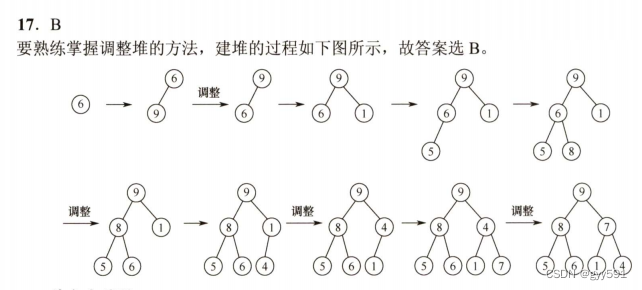
12



13

![]()

14


0
15


16

A 折半查找路径是一颗二叉排序树
17

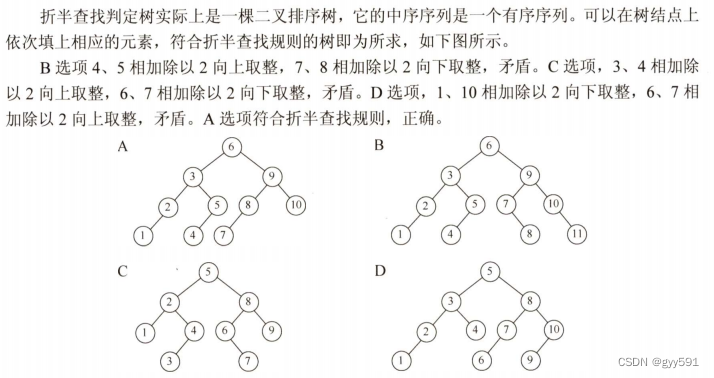
18


注意是空间复杂度

19


20


21


22

A,辅助空间都是O(1)无差
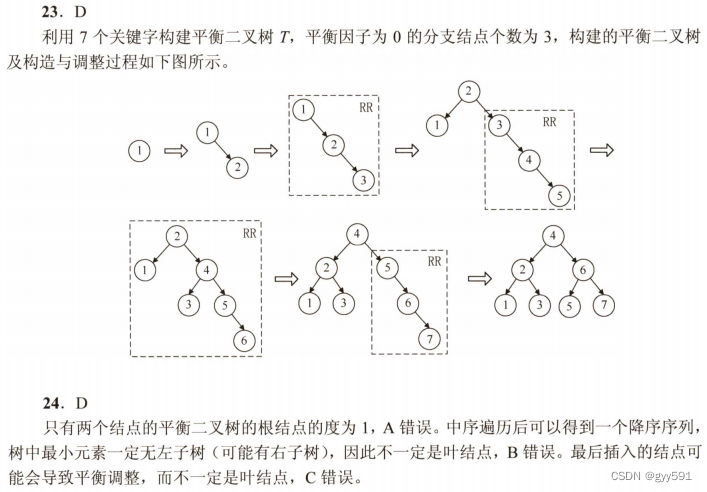
23



24

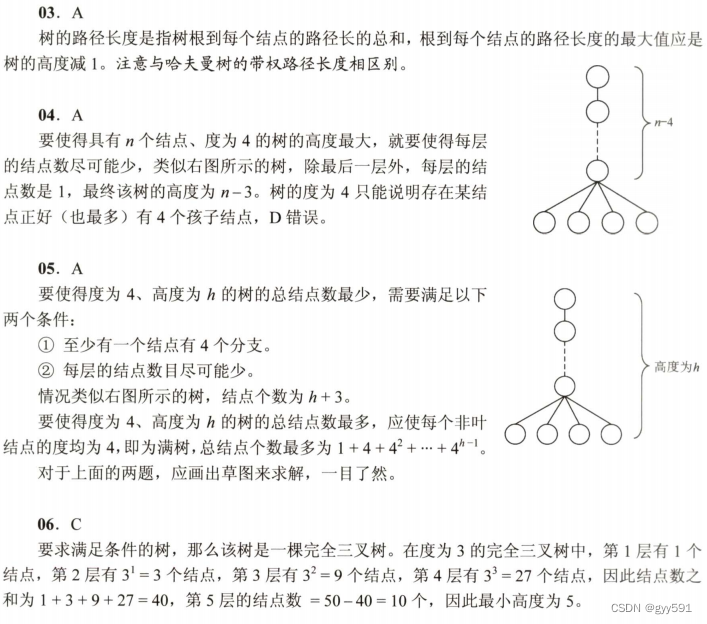



25







26


![]()



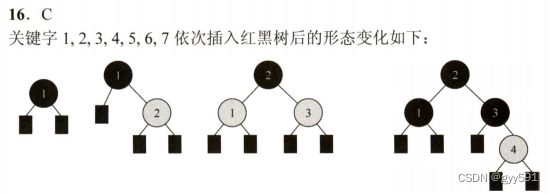


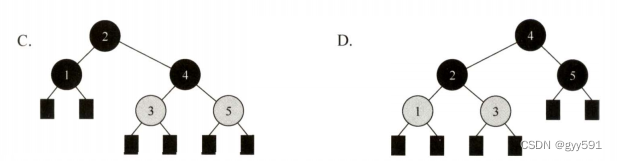

23中根节点也算分支节点


27






28



![]()


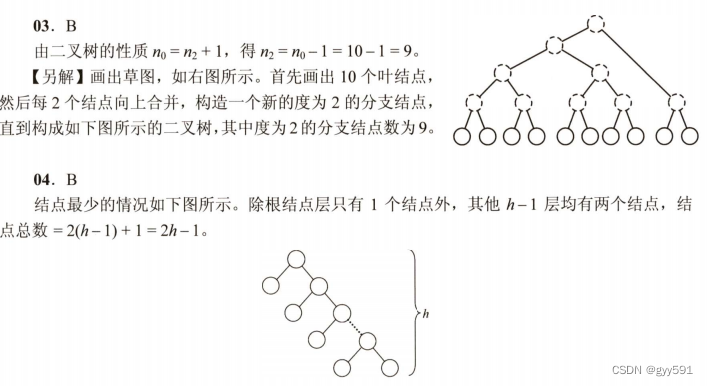
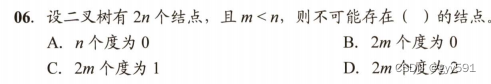







29
![]()
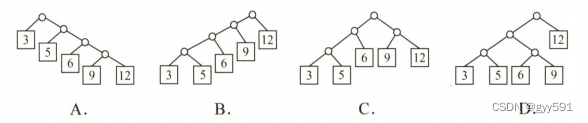








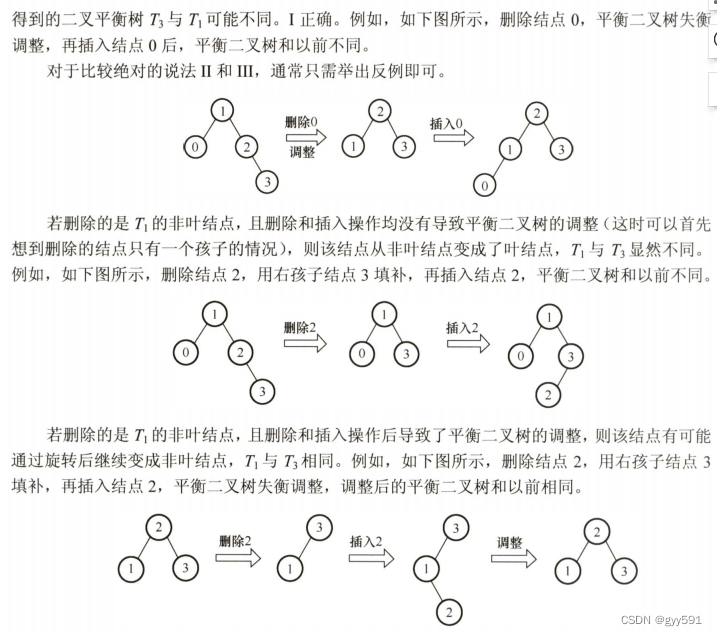
注意不是二叉树了


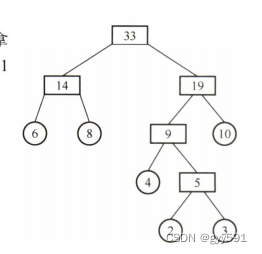
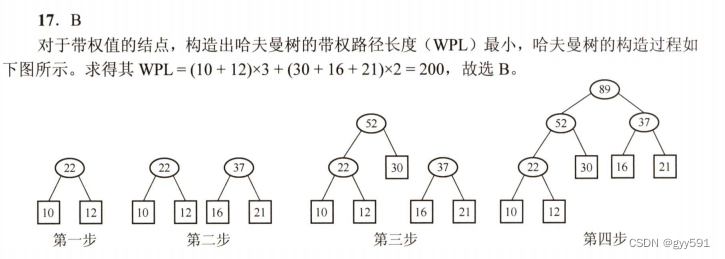
30
![]()





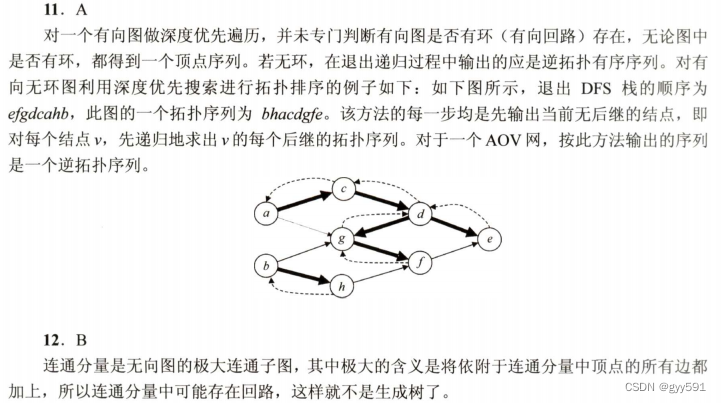

31




32






33







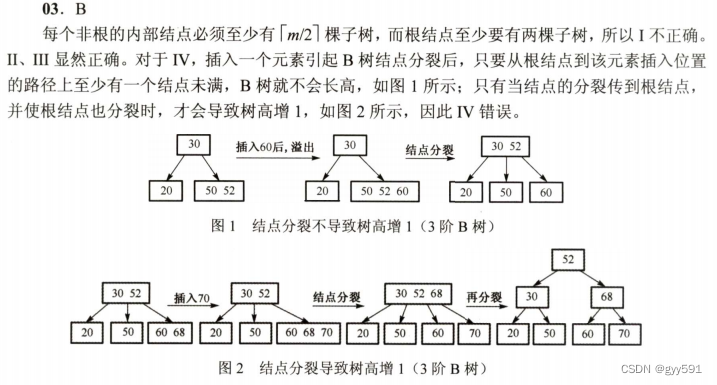




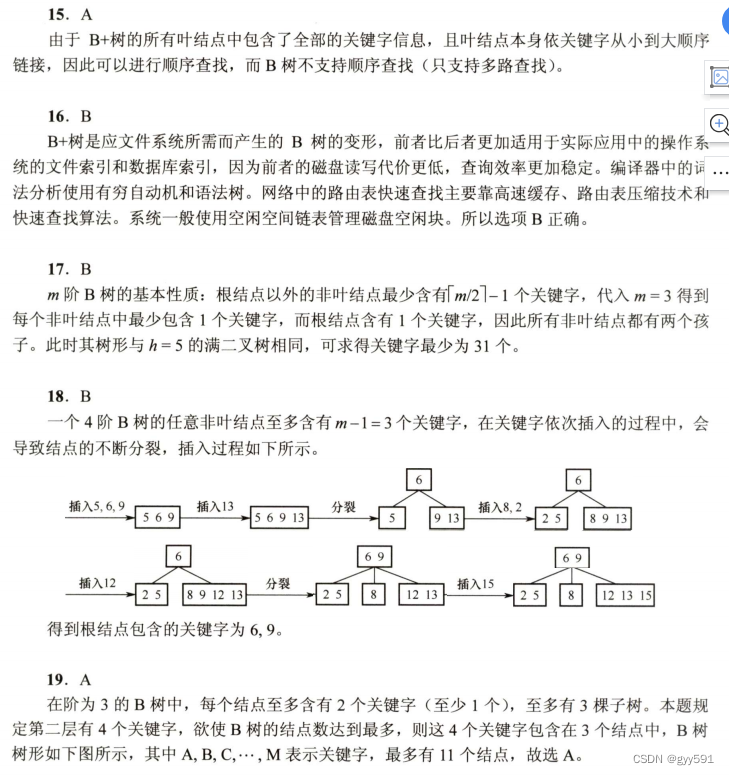

33





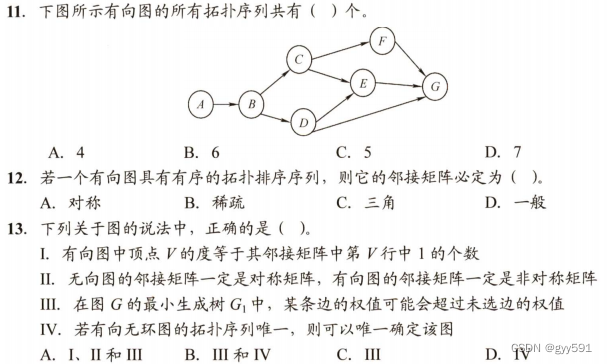

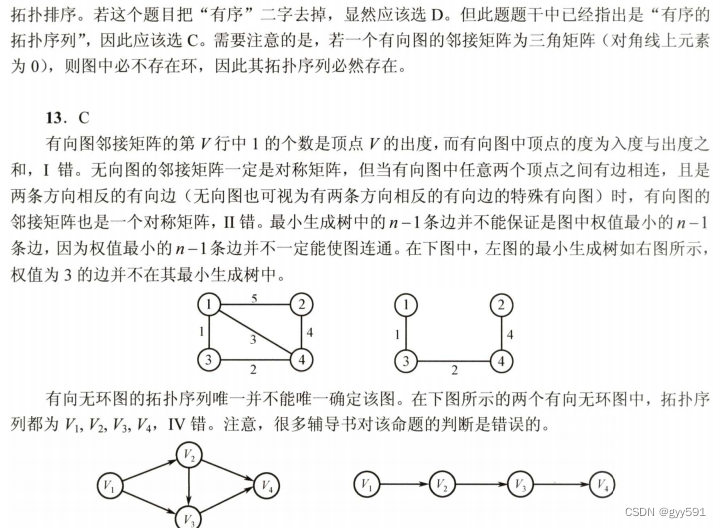



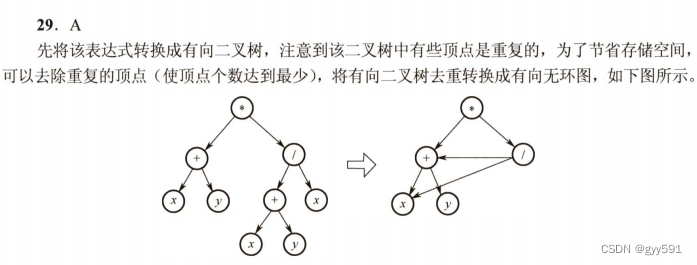
34
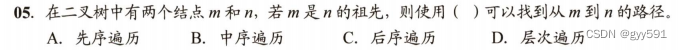







![]()







相关文章:

数据结构考研习题精选
1 A假设比较t次,由于换或不换,则必然有2^t种可能。又设有n个关键字,n!排列组合,则必然有2^t&…...
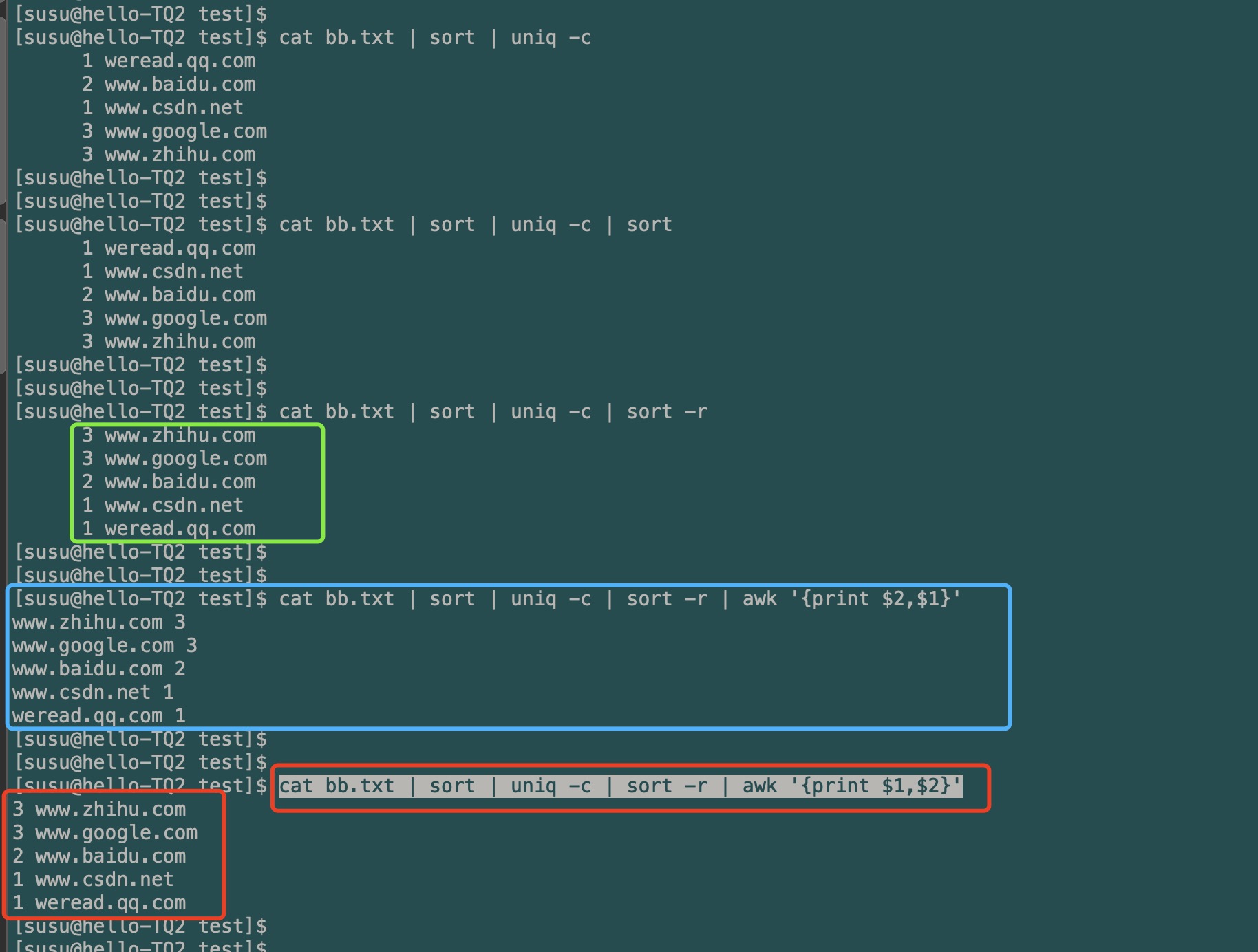
linux常用命令介绍 04 篇——uniq命令使用介绍(Linux重复数据的统计处理)
linux常用命令介绍 04 篇——uniq命令使用介绍(Linux重复数据的统计处理)1. uniq 使用语法2. sort 简单效果3. uniq 使用例子3.1 不加任何选项3.1.1 不用 sort 效果3.1.2 uniq 结合 sort 一起使用3.2 使用选项例子3.2.1 去重打印(或打印不重复…...
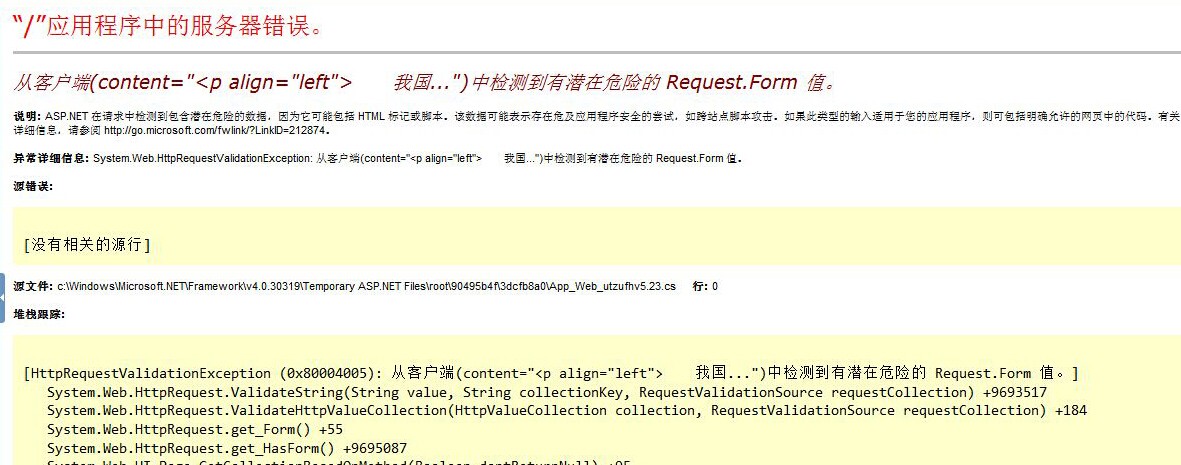
网站打不开数据库错误等常见问题解决方法
1、“主机开设成功!”上传数据后显示此内容,是因为西部数码默认放置的index.htm内容,需要核实wwwroot目录里面是否有自己的程序文件,可以删除index.htm。 2、恭喜,lanmp安装成功!这个页面是wdcp的默认页面&…...

爬虫实战进阶版【1】——某眼专业版实时票房接口破解
某眼专业版-实时票房接口破解 某眼票房接口:https://piaofang.maoyan.com/dashboard-ajax 前言 当我们想根据某眼的接口获取票房信息的时候,发现它的接口处的参数是加密的,如下图: 红色框框的参数都是动态变化的,且signKey明显是加密的一个参数。对于这种加密的参数,我们需要…...

大话数据结构-普里姆算法(Prim)和克鲁斯卡尔算法(Kruskal)
5 最小生成树 构造连通网的最小代价生成树称为最小生成树,即Minimum Cost Spanning Tree,最小生成树通常是基于无向网/有向网构造的。 找连通网的最小生成树,经典的有两种算法,普里姆算法和克鲁斯卡尔算法。 5.1 普里姆ÿ…...
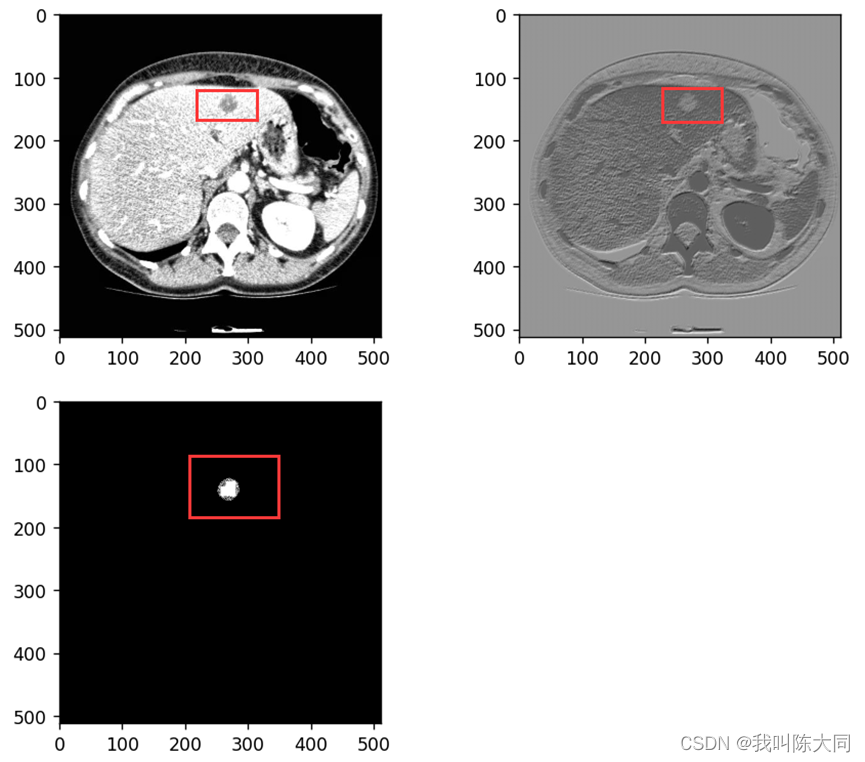
UNet-肝脏肿瘤图像语义分割
目录 一. 语义分割 二. 数据集 三. 数据增强 图像数据处理步骤 CT图像增强方法 :windowing方法 直方图均衡化 获取掩膜图像深度 在肿瘤CT图中提取肿瘤 保存肿瘤数据 四. 数据加载 数据批处理 编辑编辑 数据集加载 五. UNet神经网络模型搭建 单张图片…...

三周爆赚千万 电竞选手在无聊猿游戏赢麻了
如何用3个星期赚到1千万?普通人做梦都不敢想的事,电竞职业选手Mongraal却用几把游戏轻易完成,赚钱地点是蓝筹NFT项目Bored Ape Yacht Club(BAYC无聊猿)出品的新游戏Dookey Dash。 这款游戏类似《神庙逃亡》࿰…...

BERT学习
非精读BERT-b站有讲解视频(跟着李沐学AI) (大佬好厉害,讲的比直接看论文容易懂得多) 写在前面 在计算MLM预训练任务的损失函数的时候,参与计算的Tokens有哪些?是全部的15%的词汇还是15%词汇中真…...
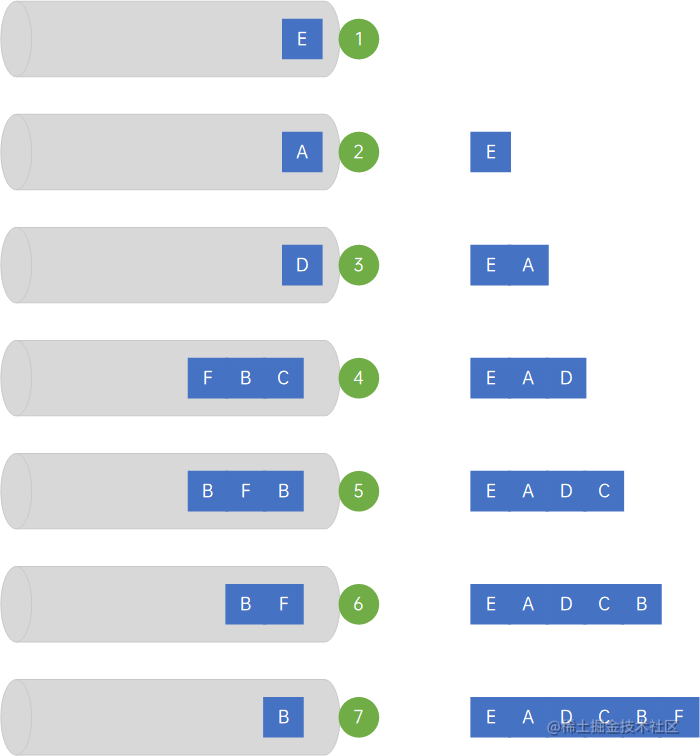
大话数据结构-图的深度优先遍历和广度优先遍历
4 图的遍历 图的遍历分为深度优先遍历和广度优先遍历两种。 4.1 深度优先遍历 深度优先遍历(Depth First Search),也称为深度优先搜索,简称DFS,深度优先遍历,是指从某一个顶点开始,按照一定的规…...

c语言指针怎么理解 第一部分
不理解指针,是因为有人教错了你。 有人告诉你,指针是“指向”某某某的,那就是误导你,给你挖了个坑。初学者小心不要误读这“指向”二字。 第一,“指针”通常用于保存一个地址,这个地址的数据类型在定义指…...
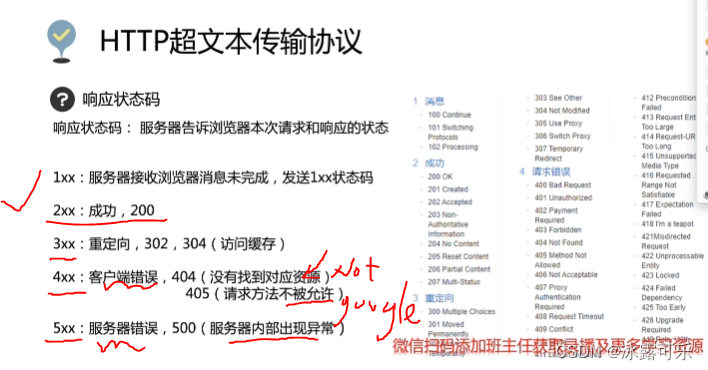
计算机网络安全基础知识2:http超文本传输协议,请求request消息的get和post,响应response消息的格式,响应状态码
计算机网络安全基础知识: 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,oracle,尤…...

Pytest自动化框架~权威教程03-原有TestSuite的执行方法
前言TestSuite一直是unittest的灵活与精髓之处, 在繁多的测试用例中, 可以任意挑选和组合各种用例集, 比如smoke用例集, level1用例集, webtest用例集, bug回归用例集等等, 当然这些TestSuite需要我们提前定义好, 并把用例加载进去.Pytest采取的是完全不同的用例组织和运行方式…...

web自动化 基于python+Selenium+PHP+Ftp实现的轻量级web自动化测试框架
1、 开发环境 win7 64 PyCharm 4.0.5 setuptools-29.0.1.zip 下载地址:setuptools-29.0.1.zip_免费高速下载|百度网盘-分享无限制 官方下载地址:setuptools PyPI python 3.3.2 mysql-connector-python-2.1.4-py3.3-win64 下载地址:mysq…...

【MyBatis】源码学习 05 - 关于 xml 文件解析的分析
文章目录前言参考目录学习笔记1、章节目录概览2、14.3:SqlSourceBuilder 类与 StaticSqlSource 类3、14.4.2:ResultMapResolver 类3.1、测试代码说明3.2、结果集 userMap 解析流程3.3、结果集 getGirl 解析流程3.4、鉴别器 discriminator 解析流程4、14.…...
代码随想录算法训练营第二天| 977. 有序数组的平方、209. 长度最小子数组、59.螺旋矩阵II
977 有序数组的平方题目链接:977 有序数组的平方介绍给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。思路看到题目的第一反应,首先负数的平方跟正数的平方是相同的&…...
Ethercat系列(10)用QT实现SOEM主站
首先将SOEM编译成静态Lib库可以参考前面的博文(83条消息) VS2017下编译SOEM(Simle Open EtherCAT Master)_soem vs_CoderIsArt的博客-CSDN博客make_libsoem_lib.bat "C:\Program Files (x86)\Microsoft Visual Studio\2017\Community\VC\Auxiliary\Build" x86用QT创建…...

论文投稿指南——中文核心期刊推荐(科学、科学研究)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...
、attr()和data())
jQuery属性操作prop()、attr()和data()
jQuery 提供了一些属性操作的方法,主要包括 prop()、attr() 和 data() 等。通过这些方法,能够实现不同的需求。下面我们分别进行详细讲解。 1.prop() 方法 prop0 方法用来设置或获取元素固有属性值。元素固有属性是指元素本身自带的属性,如 …...
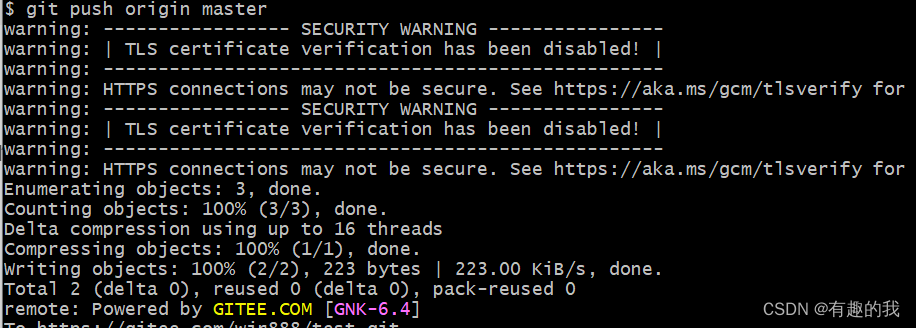
git的使用
1.git的四个区域: 2.常规git命令 git status 查看working directory哪些文件被更改了git add .把更改add到staging area,缓存的地方。改一个地方可以就先暂存一下,最后确认是哪些改动后再一起commit,以免不必要的版本。 在暂存区域ÿ…...
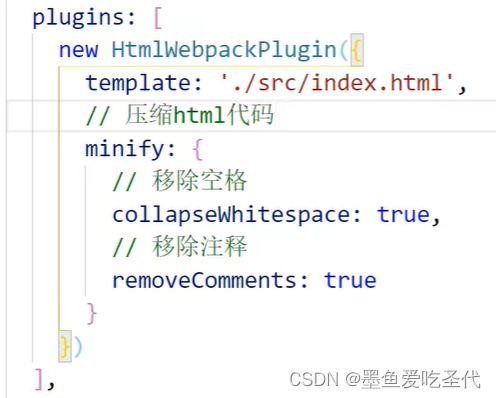
webpack生产环境配置
3 webpack生产环境配置 由于笔记文档没有按照之前的md格式书写,所以排版上代码上存在问题😢😢😢😢 09 提取css成单独文件 使用下载插件 npm i mini-css-extract-plugin0.9.0 -D webpack配置此时a,b提取成单独文件,并且…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
