朴素贝叶斯法_naive_Bayes
朴素贝叶斯法(naive Bayes)是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集,首先基于特征条件独立假设学习输入输出的联合概率分布;然后基于此模型,对给定的输入 x x x,利用贝叶斯定理求出后验概率最大的输出 y y y。
基本方法:
设输入空间 X ⊆ R n X\subseteq R^n X⊆Rn为 n n n维向量的集合,输出空间为类标记集合 Y = { c 1 , c 2 , . . . , c k } Y=\{c_1,c_2,...,c_k\} Y={c1,c2,...,ck}。输入为特征向量 x ∈ X x\in X x∈X,输出为类标记 y ∈ Y y\in Y y∈Y。 X X X是定义在输入空间 X X X上的随机向量, Y Y Y是定义在输出空间 Y Y Y上的随机变量。 P ( X , Y ) P(X,Y) P(X,Y)是 X X X和 Y Y Y的联合概率分布。训练集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} T={(x1,y1),(x2,y2),...,(xN,yN)}由 P ( X , Y ) P(X,Y) P(X,Y)独立同分布产生。
朴素贝叶斯算法就是通过训练数据集学习联合概率分布 P ( X , Y ) P(X,Y) P(X,Y)。
具体地,学习以下先验概率分布及条件概率分布。
先验概率分布: P ( Y = C k ) , k = 1 , 2 , . . . , K P(Y=C_k), \quad k=1,2,...,K P(Y=Ck),k=1,2,...,K;
条件概率分布: P ( X = x ∣ Y = C k ) = P ( X ( 1 ) = x ( 1 ) , . . . , X ( n ) = x ( n ) ∣ Y = C k ) , k = 1 , 2 , . . . , K P(X=x|Y=C_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=C_k),\quad k=1,2,...,K P(X=x∣Y=Ck)=P(X(1)=x(1),...,X(n)=x(n)∣Y=Ck),k=1,2,...,K。
由于条件概率分布 P ( X = x ∣ Y = C k ) P(X=x|Y=C_k) P(X=x∣Y=Ck)由指数级数量的参数,其估计实际是不可能的。事实上,假设特征 X ( j ) X^{(j)} X(j)可能的取值有 S j S_j Sj个, j = 1 , 2 , . . . , n j=1,2,...,n j=1,2,...,n, Y Y Y可能取值有 K K K个,那么参数个数为 K ∏ j = 1 n S j K\prod_{j=1}^{n}S_j K∏j=1nSj个。
于是朴素贝叶斯算法对条件概率分布作出了条件独立性的假设。这是一个非常强的假设,等于是说用于分类的特征在类确定的条件下都是条件独立的,具体地,条件独立性假设是
P ( X = x ∣ Y = C k ) = P ( X ( 1 ) = x ( 1 ) , . . . , X ( n ) = x ( n ) ∣ Y = C k ) P(X=x|Y=C_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=C_k) P(X=x∣Y=Ck)=P(X(1)=x(1),...,X(n)=x(n)∣Y=Ck)
= ∏ j = 1 n P ( X ( j ) = x ( j ) ∣ Y = C k ) \qquad \quad =\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=C_k) =j=1∏nP(X(j)=x(j)∣Y=Ck)
朴素贝叶斯算法在进行分类时,对给定的输入 x x x,通过学习到的模型计算后验概率分布 P ( Y = C k ∣ X = x ) P(Y=C_k|X=x) P(Y=Ck∣X=x),然后将后验概率最大的类作为 x x x的输出。后验概率计算根据贝叶斯定理进行:
P ( Y = C k ∣ X = x ) = P ( X = x ∣ Y = C k ) P ( Y = C k ) ∑ k P ( X = x ∣ Y = C k ) P ( Y = C k ) P(Y=C_k|X=x)=\frac{P(X=x|Y=C_k)P(Y=C_k)}{\sum_{k}P(X=x|Y=C_k)P(Y=C_k)} P(Y=Ck∣X=x)=∑kP(X=x∣Y=Ck)P(Y=Ck)P(X=x∣Y=Ck)P(Y=Ck)
= P ( Y = C k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = C k ) ∑ k P ( Y = C k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = C k ) \qquad \qquad \qquad \qquad=\frac{P(Y=C_k)\prod_{j}P(X^{(j)}=x^{(j)}|Y=C_k)}{\sum_{k}P(Y=C_k)\prod_{j}P(X^{(j)}=x^{(j)}|Y=C_k)} =∑kP(Y=Ck)∏jP(X(j)=x(j)∣Y=Ck)P(Y=Ck)∏jP(X(j)=x(j)∣Y=Ck)
于是,朴素贝叶斯分类器可表示为
y = f ( x ) = a r g max C k P ( Y = C k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = C k ) ∑ k P ( Y = C k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = C k ) y=f(x)=arg\max_{C_k}\frac{P(Y=C_k)\prod_{j}P(X^{(j)}=x^{(j)}|Y=C_k)}{\sum_{k}P(Y=C_k)\prod_{j}P(X^{(j)}=x^{(j)}|Y=C_k)} y=f(x)=argCkmax∑kP(Y=Ck)∏jP(X(j)=x(j)∣Y=Ck)P(Y=Ck)∏jP(X(j)=x(j)∣Y=Ck)
由于分母对所有的类都是相同的,所以
y = f ( x ) = a r g max C k P ( Y = C k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = C k ) y=f(x)=arg\max_{C_k}P(Y=C_k)\prod_{j}P(X^{(j)}=x^{(j)}|Y=C_k) y=f(x)=argCkmaxP(Y=Ck)j∏P(X(j)=x(j)∣Y=Ck)
算法:
输入:训练集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} T={(x1,y1),(x2,y2),...,(xN,yN)},其中 x i = ( x i ( 1 ) , x i ( 2 ) , . . . , x i ( n ) ) T x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)})^T xi=(xi(1),xi(2),...,xi(n))T, x i ( j ) x_i^{(j)} xi(j)是第 i i i个样本的第 j j j个特征, x i ( j ) ∈ { a j 1 , a j 2 , . . . , a j S j } x_i^{(j)} \in \{a_{j1},a_{j2},...,a_{jS_j}\} xi(j)∈{aj1,aj2,...,ajSj}, a j l a_{jl} ajl是第 j j j个特征可能取的第 l l l个值, j = 1 , 2 , . . . , n j=1,2,...,n j=1,2,...,n, l = 1 , 2 , . . . , S j l=1,2,...,S_j l=1,2,...,Sj, y i ∈ { C 1 , C 2 , . . . , C k } y_i \in \{C_1,C_2,...,C_k\} yi∈{C1,C2,...,Ck};实例 x x x。
输出:实例 x x x的分类。
- 计算先验概率及条件概率
P ( Y = C k ) = ∑ i = 1 N I ( y i = C k ) N , k = 1 , 2 , . . . , k P(Y=C_k)=\frac{\sum_{i=1}^{N}I(y_i=C_k)}{N}, \qquad k=1,2,...,k P(Y=Ck)=N∑i=1NI(yi=Ck),k=1,2,...,k
P ( X ( j ) = a j l ∣ Y = C k ) = ∑ i = 1 N I ( x ( j ) = a j l , y i = C k ) ∑ i = 1 N I ( y i = C k ) P(X^{(j)}=a_{jl}|Y=C_k)=\frac{\sum_{i=1}^{N}I(x^{(j)}=a_{jl},y_i=C_k)}{\sum_{i=1}^{N}I(y_i=C_k)} P(X(j)=ajl∣Y=Ck)=∑i=1NI(yi=Ck)∑i=1NI(x(j)=ajl,yi=Ck)
j = 1 , 2 , . . . , n ; l = 1 , 2 , . . . , S j ; k = 1 , 2 , . . . , K \qquad j=1,2,...,n; \quad l=1,2,...,S_j; \quad k=1,2,...,K j=1,2,...,n;l=1,2,...,Sj;k=1,2,...,K- 对于给定实例 x = ( x ( 1 ) , x ( 2 ) , . . . , x ( n ) ) T x={(x^{(1)},x^{(2)},...,x^{(n)})}^T x=(x(1),x(2),...,x(n))T,计算(这里用到了特征条件独立假设)
P ( Y = C k ) ∏ j = 1 n P ( X ( j ) = x ( j ) ∣ Y = C k ) , k = 1 , 2 , . . . , K P(Y=C_k)\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=C_k),\qquad k=1,2,...,K P(Y=Ck)j=1∏nP(X(j)=x(j)∣Y=Ck),k=1,2,...,K- 确定实例 x x x的分类
y = a r g max C k P ( Y = C k ) ∏ j = 1 n P ( X ( j ) = x ( j ) ∣ Y = C k ) y=arg\max_{C_k}P(Y=C_k)\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=C_k) y=argCkmaxP(Y=Ck)j=1∏nP(X(j)=x(j)∣Y=Ck)
相关文章:

朴素贝叶斯法_naive_Bayes
朴素贝叶斯法(naive Bayes)是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集,首先基于特征条件独立假设学习输入输出的联合概率分布;然后基于此模型,对给定的输入 x x x,利用贝叶斯定理…...
Windows下安装MongoDB实践总结
本文记录Windows环境下的MongoDB安装与使用总结。 【1】官网下载 官网下载地址:Download MongoDB Community Server | MongoDB 这里可以选择下载zip或者msi,zip是解压后自己配置,msi是傻瓜式一键安装。这里我们分别对比进行实践。 【2】ZI…...
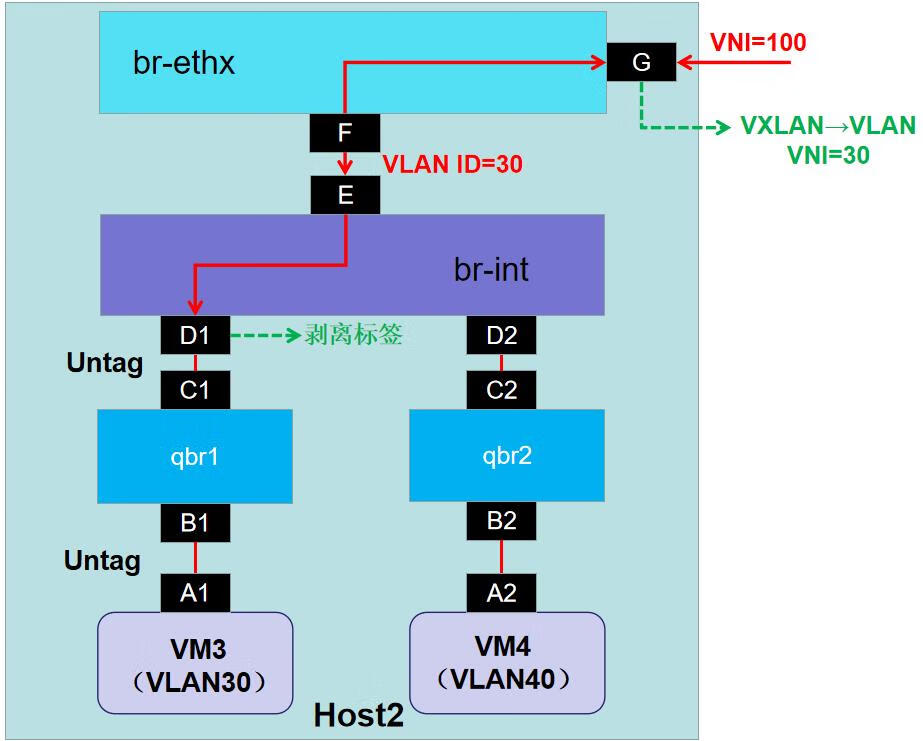
华为云Stack 8.X 流量模型分析(二)
二、流量模型分析相关知识 1.vNIC 虚拟网络接口卡(vNIC)是基于主机物理 NIC 的虚拟网络接口。每个主机可以有多个 NIC,每个 NIC 可以是多个 vNIC 的基础。 将 vNIC 附加到虚拟机时,Red Hat Virtualization Manager 会在虚拟机之间创建多个关联的…...
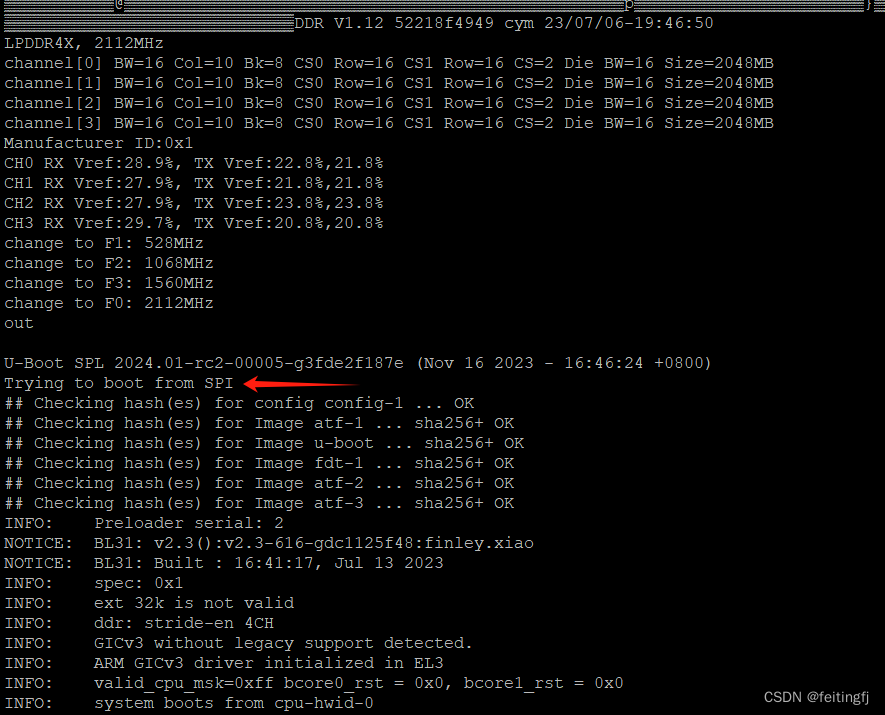
rk3588 之启动
目录 uboot版本配置修改编译 linux版本配置修改编译 启动sd卡启动制作spi 烧录 参考 uboot 版本 v2024.01-rc2 https://github.com/u-boot/u-boot https://github.com/rockchip-linux/rkbin 配置修改 使用这两个配置即可: orangepi-5-plus-rk3588_defconfig r…...
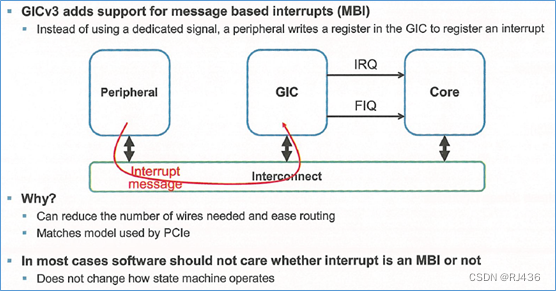
ARM GIC (五)gicv3架构-LPI
在gicv3中,引入了一种新的中断类型。message based interrupts,消息中断。 一、消息中断 外设,不在通过专用中断线,向gic发送中断,而是写gic的寄存器,来发送中断。 这样的一个好处是,可以减少中断线的个数。 为了支持消息中断,gicv3,增加了LPI,来支持消息中断。并且…...
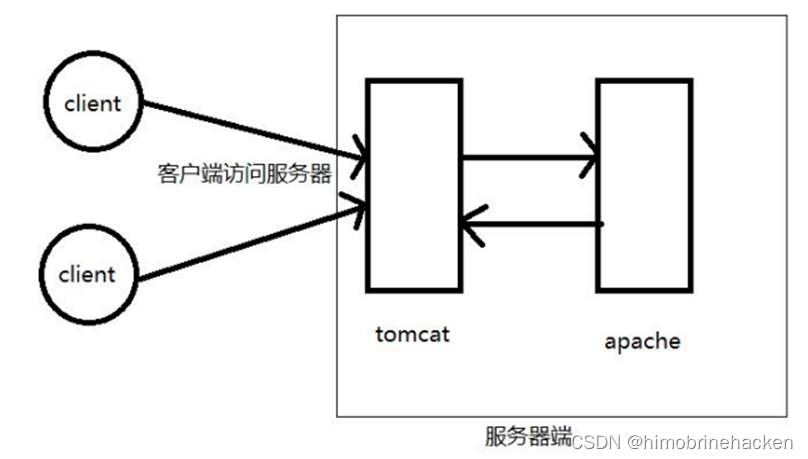
sql-labs服务器结构
双层服务器结构 一个是tomcat的jsp服务器,一个是apache的php服务器,提供服务的是php服务器,只是tomcat向php服务器请求数据,php服务器返回数据给tomcat。 此处的29-32关都是这个结构,不是用docker拉取的镜像要搭建一下…...
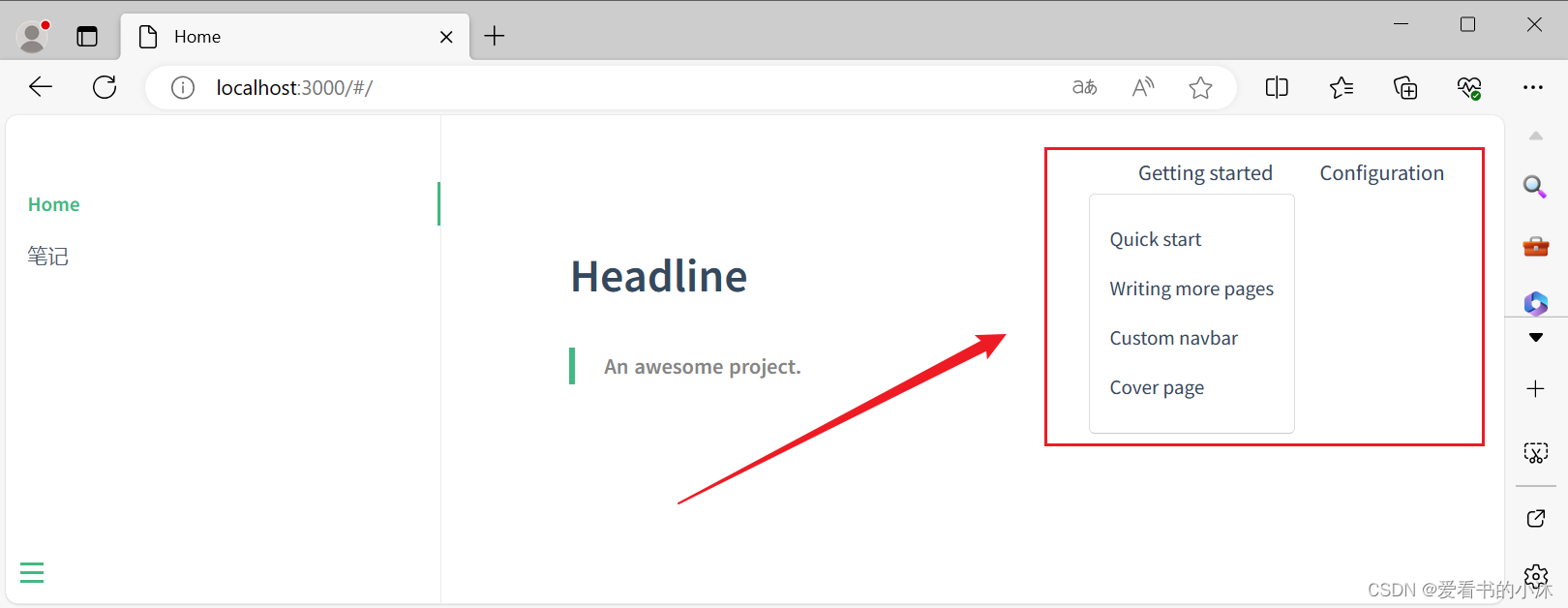
【小沐学写作】Docsify制作在线电子书、技术文档(Docsify + Markdown + node)
文章目录 1、简介2、安装2.1 node2.2 docsify-cli 3、配置3.1 初始化3.2 预览效果3.3 加载对话框3.4 更多页面3.5 侧 栏3.6 自定义导航栏 结语 1、简介 https://docsify.js.org/#/?iddocsify 一个神奇的文档网站生成器。 简单轻巧没有静态构建的 html 文件多个主题 Docsify…...
电脑完全重装教程——原版系统镜像安装
注意事项 本教程会清除所有个人文件 请谨慎操作 请谨慎操作 请谨慎操作 前言 本教程是以系统安装U盘为介质进行系统重装操作,照着流程操作会清除整个硬盘里的文件,请考虑清楚哦~ 有些小伙伴可能随便在百度上找个WinPE作为启动盘就直接…...
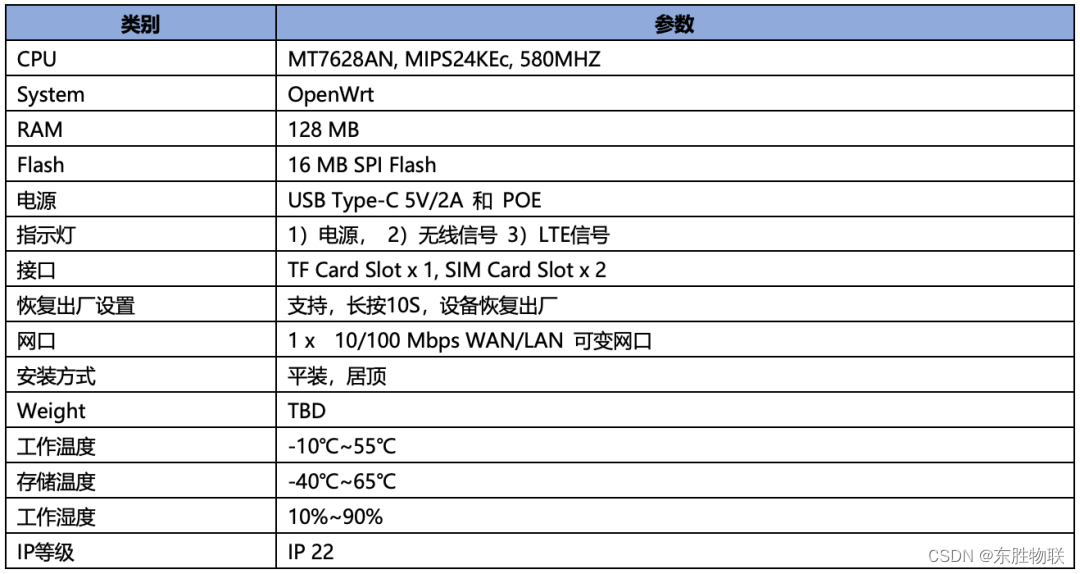
【智慧办公】如何让智能会议室的电子标签实现远程、批量更新信息?东胜物联网硬件网关让解决方案更具竞争力
近年来,为了减少办公耗能、节能环保、降本增效,越来越多的企业开始从传统的办公模式转向智慧办公。 以智能会议室为例,会议是企业业务中不可或缺的一部分,但在传统办公模式下,一来会议前行政人员需要提前准备会议材料…...
静态工厂方法模式)
面向对象设计与分析40讲(16)静态工厂方法模式
前面我们介绍了简单工厂模式,在创建对象前,我们需要先创建工厂,然后再通过工厂去创建产品。 如果将工厂的创建方法static化,那么无需创建工厂即可通过静态方法直接调用的方式创建产品: // 工厂类,定义了静…...

【贪心】买卖股票的最佳时机含手续费
/** 贪心:每次选取更低的价格买入,遇到高于买入的价格就出售(此时不一定是最大收益)。* 使用buy表示买入股票的价格和手续费的和。遍历数组,如果后面的股票价格加上手续费* 小于buy,说明有更低的买入价格更新buy。如…...

Altium Designer入门到就业【目录】
🏡《AD目录》 欢迎大家来到《Altium Designer入门到就业》该专栏包括【电路设计篇】【PCB设计篇】【电路仿真篇】【PCB仿真篇】四个部分,以供大家参考。大家直接点击大纲中蓝色标题即可轻松传送。 【电路设计篇】 Altium Designer(AD24&#…...

cmake 查看编译命令,以及在vscode中如何使用cmke
通过设置如下配置选项,可以生成compile_commands.json 文件,记录使用的编译命令 set(CMAKE_EXPORT_COMPILE_COMMANDS ON)获得现有模块列表 cmake --help-module-list查看命令文档 cmake --help-command find_file查看模块的详细信息 cmake --help-mo…...

玩转 Scrapy 框架 (一):Scrapy 框架介绍及使用入门
目录 一、Scrapy 框架介绍二、Scrapy 入门 一、Scrapy 框架介绍 简介: Scrapy 是一个基于 Python 开发的爬虫框架,可以说它是当前 Python 爬虫生态中最流行的爬虫框架,该框架提供了非常多爬虫的相关组件,架构清晰,可扩…...
node.js mongoose index(索引)
目录 简介 索引类型 单索引 复合索引 文本索引 简介 在 Mongoose 中,索引(Index)是一种用于提高查询性能的数据结构,它可以加速对数据库中文档的检索操作 索引类型 单索引、复合索引、文本索引、多键索引、哈希索引、地理…...

谷歌推大语言模型VideoPoet:文本图片皆可生成视频和音频
Google Research最近发布了一款名为VideoPoet的大型语言模型(LLM),旨在解决当前视频生成领域的挑战。该领域近年来涌现出许多视频生成模型,但在生成连贯的大运动时仍存在瓶颈。现有领先模型要么生成较小的运动,要么在生…...

ES-mapping
类似数据库中的表结构定义,主要作用如下 定义Index下的字段名( Field Name) 定义字段的类型,比如数值型、字符串型、布尔型等定义倒排索引相关的配置,比如是否索引、记录 position 等 index_options 用于控制倒排索记录的内容,有如…...

Centos 7.9安装Oracle19c步骤亲测可用有视频
视频介绍了在虚拟机安装centos 7.9并安装数据库软件的全过程 视频链接:https://www.zhihu.com/zvideo/1721267375351996416 下面的文字描述是安装数据库的部分介绍 一.安装环境准备 链接:https://pan.baidu.com/s/1Ogn47UZQ2w7iiHAiVdWDSQ 提取码&am…...
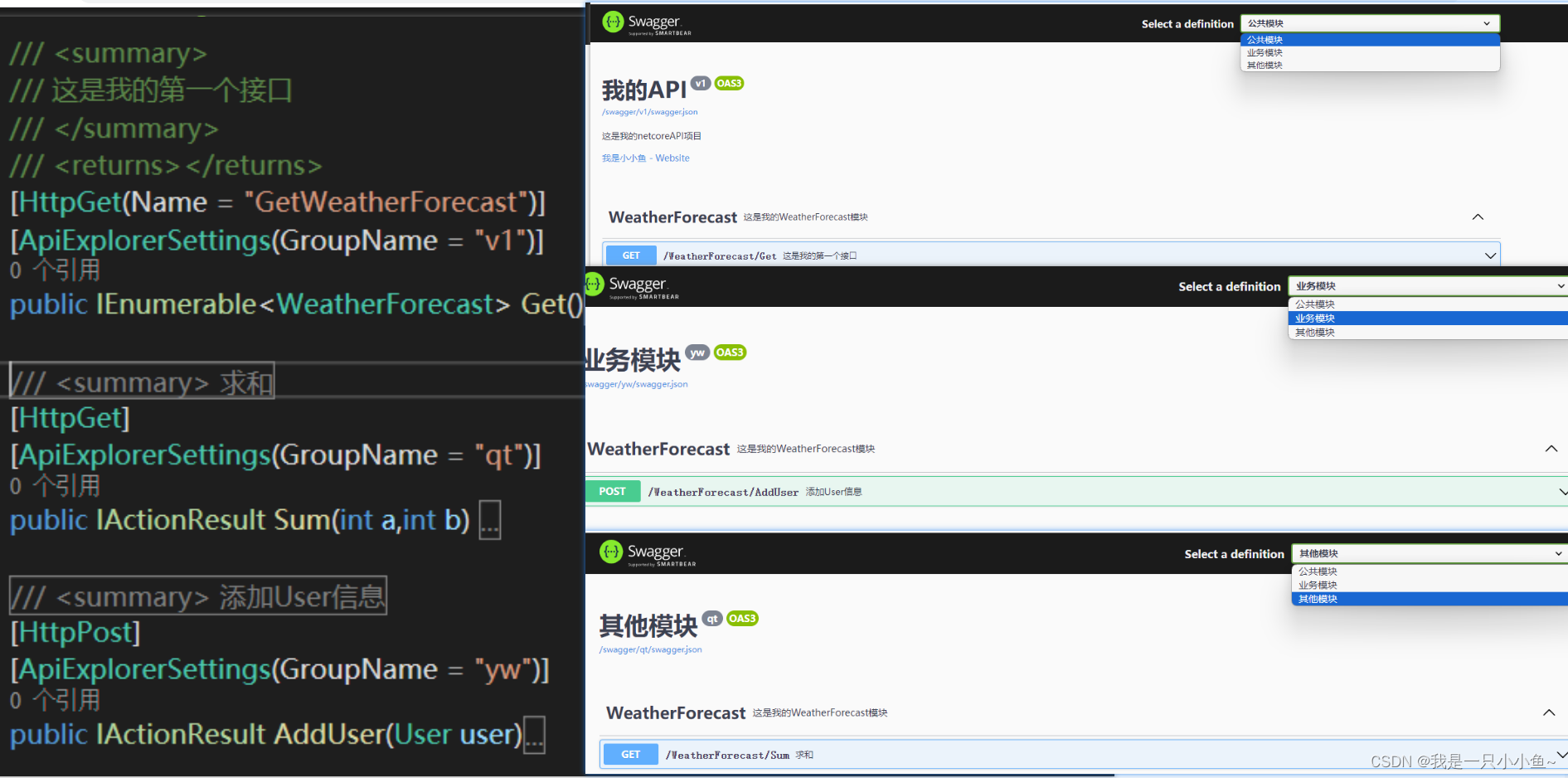
.NET中的Swagger使用
目录 前言 一、Swagger是什么? 二、如何Swagger文档说明的信息 1.在AddSwaggerGen方法中写入文档信息 2.运行效果 二、文档UI界面标题、路由设置 1.在中间件UseSwaggerUI方法中配置 三、文档UI界面添加接口注释 1.在 .csproj中配置 2.在AddSwaggerGen方法中配置Incl…...

结构屈曲分析
结构屈曲分析主要用于判定结构受载后是否有失稳风险,作为工程应用,一般分为线性屈曲分析和非线性屈曲分析。 线性屈曲分析需要具备较多的前提条件,如载荷无偏心、材料无缺陷等,在实际工程应用中结构制作过程和加载方式很难达到线性…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...
