C++面试宝典第9题:找出第K大元素
题目
给定一个整数数组a,同时给定它的大小N和要找的K(1 <= K <= N),请根据快速排序的思路,找出数组中第K大的数(保证答案存在)。比如:数组a为[50, 23, 66, 18, 72],数组大小N为5,K为3,则第K大的数为50。

解析
这道题主要考察应聘者对于快速排序的理解,以及实际运用的能力。快速排序是一种高效的排序算法,采用分治策略进行排序。以下是快速排序的具体步骤:
选择轴心(pivot):首先,从待排序的数组中选择一个元素作为轴心。选择轴心的方式有多种,可以选择第一个元素、最后一个元素、中间元素,或者随机选择一个元素。
划分(Partition):重新排列数组,使得所有比轴心小的元素都排在轴心的左边,所有比轴心大的元素都排在轴心的右边。在这个过程中,轴心的位置也确定了。
递归排序子数组:递归地对轴心左边和右边的两个子数组进行快速排序。递归的终止条件是:子数组的长度为1或0,此时子数组已经有序。
根据上面的分析,我们可以写出快速排序的示例代码。
int Partition(int* pnNumber, int 相关文章:

C++面试宝典第9题:找出第K大元素
题目 给定一个整数数组a,同时给定它的大小N和要找的K(1 <= K <= N),请根据快速排序的思路,找出数组中第K大的数(保证答案存在)。比如:数组a为[50, 23, 66, 18, 72],数组大小N为5,K为3,则第K大的数为50。 解析 这道题主要考察应聘者对于快速排序的理解,以及实…...

“马屁精”李白
“李白一斗诗百篇,长安市上酒家眠。天子呼来不上船,自称臣是酒中仙。”这是诗圣杜甫笔下的李白,也是我们脑海里坚信无二的李白。恃才傲物又狂放不羁的诗仙,怎么会低眉顺眼地去拍人马屁呢? 但我要说的是,人…...

python之glob的用法
目录 获取特定扩展名的所有文件 获取特定目录下的所有文件 递归获取所有文件 转义特殊字符 iglob glob 是 Python 中用于文件模式匹配的一个模块。它使用 Unix shell-style 的通配符来进行匹配,并返回所有匹配的文件路径列表。 下面是一些 glob 的基本用法&am…...

【adb】电脑通过ADB向手机传输文件
具体步骤如下: Step1 下载ADB工具 下载最新版本的 ADB工具 !!! 注意:一定要是最新版本的ADB,否则很可能导致无法识别到手机。 将下载的ADB解压以后的文件如下图所示: Step2 添加环境变量 将 ADB的路径 D:\platformtools &…...

npm的常用使用技巧
npm是一个强大的工具,可以帮助你管理Node.js项目中的依赖项。以下是一些有用的npm使用技巧: 使用npm install命令:这个命令可以安装项目的依赖项。如果你想安装一个特定的版本,你可以使用npm install <package><version…...

【网络奇遇记】揭秘计算机网络的性能指标:速率|带宽|吞吐量|时延
🌈个人主页:聆风吟 🔥系列专栏:网络奇遇记、数据结构 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. 速率1.1 数据量1.2 速率 二. 带宽三. 吞吐量四. 时延4.1 发送时延4.2 传播时延…...

ACM中算法时间约束
ACM中算法时间约束 一般ACM竞赛C/C的时间限制是一秒,因此可以根据题目数据来推断该题所使用的算法。 算法的时间复杂度在 1 0 7 10^7 107左右合适,最多不能超过 1 0 8 10^8 108, O ( n ) O(n) O(n)的极限就在 1 0 8 10^8 108左右。 问题规…...
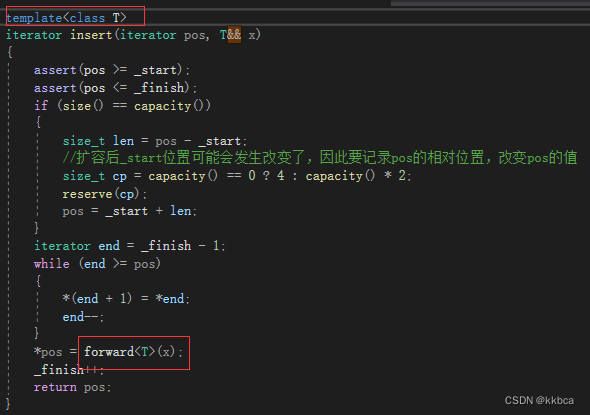
C++11的列表初始化和右值引用
目录 前言 一、C11的简介 二、C11的小故事。 三、统一的列表初始化 1.列表初始化 2.initializer_list 四、右值引用 1.什么是左值 2.什么是右值 3.右值引用写法 4.右值的分类 5.右值引用的作用 6.STL容器中的右值引用 7.万能引用 总结 前言 C11相较于之C98&…...

千帆起航:探索百度智能云千帆AppBuilder在AI原生应用开发中的革新之路
千帆起航:探索百度千帆AppBuilder在AI原生应用开发中的革新之路 1.揭开帷幕,大模型第二次战役 自从 ChatGPT 横空出世后,一石激起千层浪,人工智能也正在从感知理解走向生成创造,这是一个关键里程碑。生成式大模型完成…...
RevIT™ AAV Enhancer, 提高AAV产量的又一利器!
腺相关病毒 (AAV) 是基因治疗中使用最广泛的传递机制。近年来,基于AAV病毒所开发的基因疗法的研发及临床试验注册数量也呈指数级增长。截止本文撰写之时,美国食品和药物管理局已批准五项AAV疗法,也是全球市场上最为昂贵的药物,其中…...
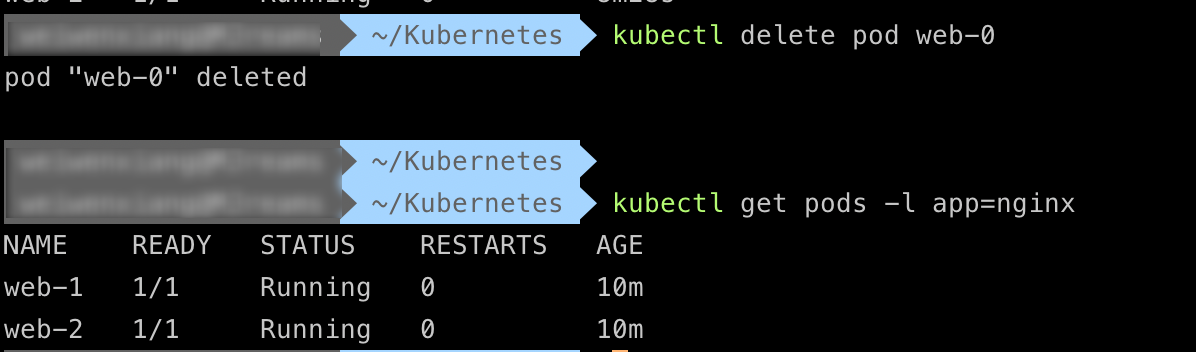
Kubectl 部署有状态应用(下)
接上文 《Kubectl 部署有状态应用(上)》创建完StatefulSet后,本文继续介绍StatefulSet 扩展、更新、删除等内容。 StatefulSet 中的 Pod 验证序数索引和稳定的网络身份 StatefulSet 中的 Pod 具有唯一的序数索引和稳定的网络身份。 查看 …...

Jmeter 性能 —— 监控服务器!
Jmeter监控Linux需要三个文件 JMeterPlugins-Extras.jar (包:JMeterPlugins-Extras-1.4.0.zip)JMeterPlugins-Standard.jar (包:JMeterPlugins-Standard-1.4.0.zip)ServerAgent-2.2.3.zip 1、Jemter 安装插件 在插件管理中心的搜索Servers Performan…...

离散型制造企业为什么要注重MES管理系统的实施
离散型制造企业经常面临三个核心问题:生产什么、生产多少以及如何生产。尽管许多企业都实施了ERP系统,但仍然绕不开MES管理系统的话题。本文将从三个方面详细解释为什么离散型企业需要实施MES管理系统。 一、生产线经常出现的问题 在离散型企业中&#…...

Linux系统中跟TCP相关的内核参数
1. TCP保活机制 参考 《Nginx(三) 配置文件详解 - 基础模块》3.18章节 net.ipv4.tcp_keepalive_intvl:设置两次相邻探活检测的间隔时间。默认是75秒,单位是秒。net.ipv4.tcp_keepalive_probes:设置探活最多检测次数。默认是9次,单…...
)
代理模式(Proxy)
代理模式(Proxy Pattern)是一种结构型设计模式,用于为另一个对象提供一个代替品或占位符以控制对这个对象的访问。这个模式主要用于延迟处理操作或者在进行实际操作前后进行其它处理。 代理模式的实现通常涉及以下角色: 抽象主题(Subject):定义了代理和真实对象的共用接…...

在MacOS上Qt配置OpenCV并进行测试
目录 一.Qt环境准备 二.在Qt项目中加载Opencv库并编写代码测试 1.使用Opencv加载图片 (1)在Qt中创建一个新项目 (2)在.pro文件中链接OpenCV库 (3)添加新资源文件 (4)在mainw…...
java数据结构与算法刷题-----LeetCode167:两数之和 II - 输入有序数组
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 思路 题目要求我们找到两个数相加的和,等于target指定的值。而…...
Linux:jumpserver V3的安装与升级(在线离线)(2)
官方文档写的非常详细,我这篇文章时间长了,会随着官方版本更新而落后 JumpServer - 开源堡垒机 - 官网https://www.jumpserver.org/安装和升级在官网也有详细的信息,我写本章是为了记录一下实验 我的系统是centos7.9 在线安装 在确定我们可…...
【GoLang】Go语言几种标准库介绍(一)
你见过哪些令你膛目结舌的代码技巧? 文章目录 你见过哪些令你膛目结舌的代码技巧?前言几种库bufio(带缓冲的 I/O 操作)特性示例 bytes (实现字节操作)特性示例 总结专栏集锦写在最后 前言 随着计算机科学的迅猛发展,编…...

短剧分销系统:月入百w的新模式
随着我国短剧的高速发展,越来越多的人进入到了短剧影视行业。本文旨在介绍短剧市场的发展前景以及短剧分销系统的设计和开发。 一、短剧发展背景 短剧具有时长短、剧情紧凑、节奏快、剧情新颖等特点,满足了国内观众的碎片化时间,在当下短视频…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
