力扣labuladong一刷day46天并查集
力扣labuladong一刷day46天并查集
文章目录
- 力扣labuladong一刷day46天并查集
- 一、323. 无向图中连通分量的数目
- 二、130. 被围绕的区域
- 三、990. 等式方程的可满足性
一、323. 无向图中连通分量的数目
题目链接:https://leetcode.cn/problems/number-of-connected-components-in-an-undirected-graph/description/
思路:求联通分量一般是通过并查集,而构建并查集则非常简单,使用一个数组模拟森林,每个槽位记录对应的父节点,合并两个集合时只需要把一个根节点作为另一个根节点的子节点,此外为了提升效率,在查询根节点的过程中可以采用压缩路径的方法,即不断的让当前节点与其父节点做兄弟。
class Solution {public int countComponents(int n, int[][] edges) {UF uf = new UF(n);for (int[] edge : edges) {uf.union(edge[0], edge[1]);}return uf.count;}class UF {int[] parent;int count;public UF(int n) {parent = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;}count = n;}int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}boolean connected(int x, int y) {return find(x) == find(y);}void union(int x, int y) {int p = find(x);int q = find(y);if (p == q) return;parent[p] = q;count--;}}
}
二、130. 被围绕的区域
题目链接:https://leetcode.cn/problems/surrounded-regions/
思路:这是一个岛屿问题,也是棋盘问题,其实描述的是一件事情。一般采用dfs解决。本题要求与边界不相邻的修改为X,与边界相邻的不动。其实我们可以只dfs与边界相邻的,修改为A。之后直接for循环遍历棋盘,把O改为X,把A改为O。
class Solution {public void solve(char[][] board) {int row = board.length, col = board[0].length;for (int i = 0; i < row; i++) {if (board[i][0] == 'O') dfs(board, i, 0);if (board[i][col-1] == 'O') dfs(board, i, col-1);}for (int i = 0; i < col; i++) {if (board[0][i] == 'O') dfs(board, 0, i);if (board[row-1][i] == 'O') dfs(board, row-1, i);}for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {if (board[i][j] == 'O') board[i][j] = 'X';if (board[i][j] == 'A') board[i][j] = 'O';}}}void dfs(char[][] board, int x, int y) {if (x < 0 || x >= board.length || y < 0 || y >= board[0].length || board[x][y] != 'O') return;board[x][y] = 'A';dfs(board, x-1, y);dfs(board, x+1, y);dfs(board, x, y-1);dfs(board, x, y+1);}
}
三、990. 等式方程的可满足性
题目链接:https://leetcode.cn/problems/satisfiability-of-equality-equations/
思路:把相等的进行连接,然后逐个判断不等的看看是否在一个联通里,如果不等的在一个联通里即不满住可满足性。
class Solution {public boolean equationsPossible(String[] equations) {UF uf = new UF(26);for (String s : equations) {if (s.charAt(1) == '=') {uf.union(s.charAt(0)-'a', s.charAt(3)-'a');}}for (String s : equations) {if (s.charAt(1) == '!') {if (uf.connected(s.charAt(0)-'a', s.charAt(3)-'a')) {return false;}}}return true;}class UF {int[] parent;int count;public UF(int n) {parent = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;}count = n;}int find(int x) {if (x != parent[x]) {parent[x] = find(parent[x]);}return parent[x];}boolean connected(int x, int y) {return find(x) == find(y);}void union(int x, int y) {int a = find(x);int b = find(y);if (a == b)return;parent[a] = b;count--;}}
}
相关文章:

力扣labuladong一刷day46天并查集
力扣labuladong一刷day46天并查集 文章目录 力扣labuladong一刷day46天并查集一、323. 无向图中连通分量的数目二、130. 被围绕的区域三、990. 等式方程的可满足性 一、323. 无向图中连通分量的数目 题目链接:https://leetcode.cn/problems/number-of-connected-co…...
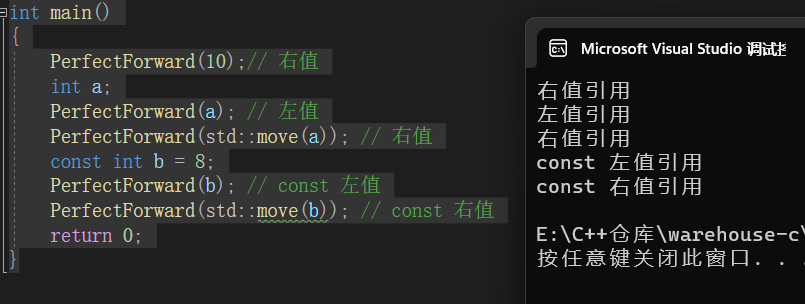
C++11(上):新特性讲解
C11新特性讲解 前言1.列表初始化1.1{ }初始化1.2std::initializer_list 2.类型推导2.1 auto2.2 typeid2.3 decltype 3.范围for4.STL的变化4.1新容器4.2容器的新方法 5.右值引用和移动语义5.1 左值引用和右值引用5.2 左值引用与右值引用比较5.3 右值引用的使用场景5.4 右值、左值…...
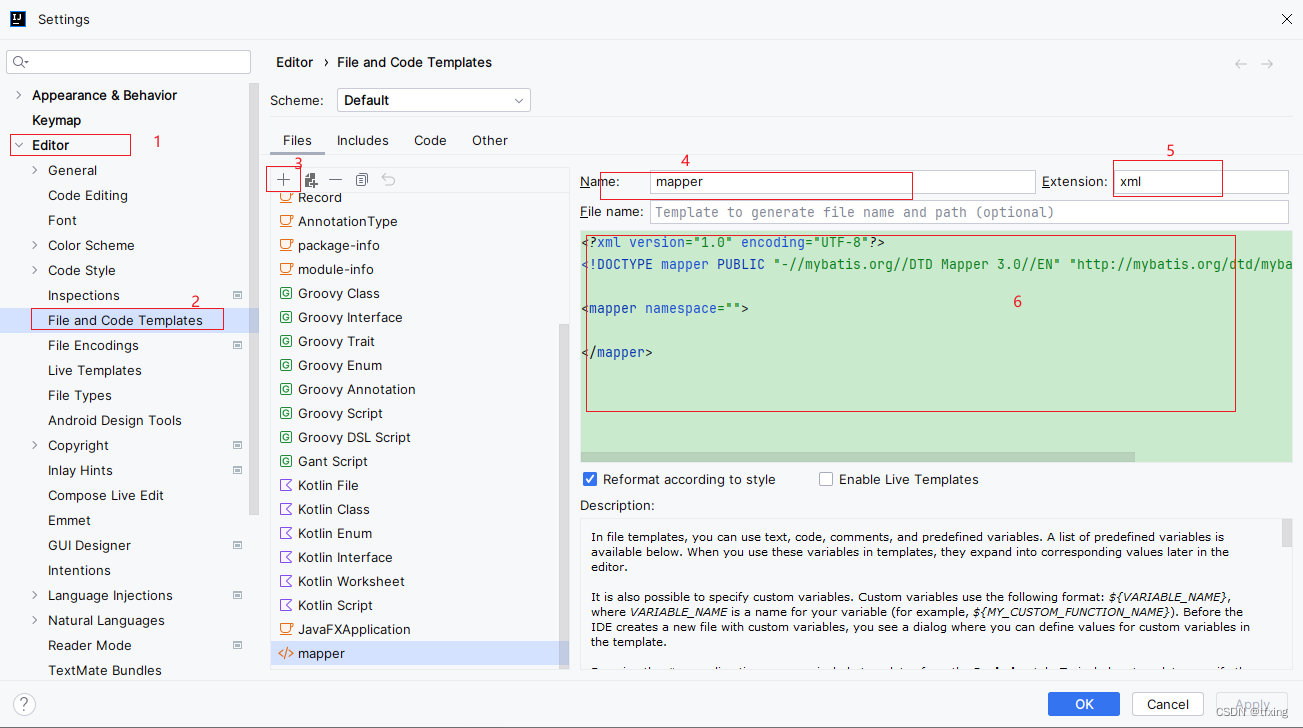
将mapper.xml保存为idea的文件模板
将mapper.xml保存为idea的文件模板 在idea的File and Code Templates中将需要使用模板的内容添加为模板文件。 那么接下来请看图,跟着步骤操作吧。 mapper.xml文件内容 <?xml version"1.0" encoding"UTF-8"?> <!DOCTYPE mapper P…...

LabVIEW在横向辅助驾驶系统开发中的应用
LabVIEW在横向辅助驾驶系统开发中的应用 随着横向辅助驾驶技术的快速发展,越来越多的研究致力于提高该系统的效率和安全性。项目针对先进驾驶辅助系统(ADAS)中的横向辅助驾驶进行深入研究。在这项研究中,LabVIEW作为一个强大的系…...
STM32移植LVGL图形库
1、问题1:中文字符keil编译错误 解决方法:在KEIL中Options for Target Flash -> C/C -> Misc Controls添加“--localeenglish”。 问题2:LVGL中显示中文字符 使用 LVGL 官方的在线字体转换工具: Online font converter -…...

迪文屏开发保姆级教程5—表盘时钟和文本RTC显示
这篇文章要讲啥事呢? 本篇文章主要介绍了在DGBUS平台上使用表盘时钟和文本时钟RTC显示功能的方法。 文哥悄悄话: 官方开发指南PDF:(不方便下载的私聊我发给你) https://download.csdn.net/download/qq_21370051/8864…...

免费IDEA插件推荐-Apipost-Helper
IDEA插件市场中的API调试插件不是收费(Fast Request )就是不好用(apidoc、apidocx等等)今天给大家介绍一款国产的API调试插件:Apipost-Helper,完全免费且好看好用! 这款插件由Apipost团队开发的…...

Django(二)
1.django框架 1.1 安装 pip install django3.21.2 命令行 创建项目 cd 指定目录 django-admin startproject 项目名mysite ├── manage.py [项目的管理工具] └── mysite├── __init__.py├── settings.py 【配置文件,只有一部分…...
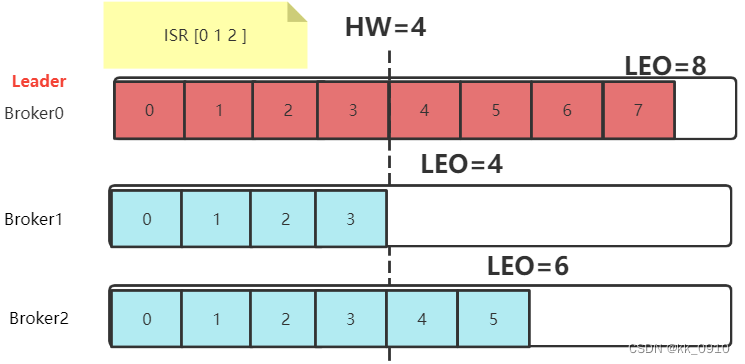
Kafka集群架构服务端核心概念
目录 Kafka集群选举 controller选举机制 Leader partition选举 leader partition自平衡 partition故障恢复机制 follower故障 leader故障 HW一致性保障 HW同步过程 Epoch Kafka集群选举 1. 在多个broker中, 需要选举出一个broker, 担任controller. 由controller来管理…...

【vscode插件】之插件图标设置
ChatgGPT4.0国内站点: 海鲸AI-支持GPT(3.5/4.0),文件分析,AI绘图 在Visual Studio Code中创建插件时,你可以为你的插件设置一个图标,这个图标会在VS Code的插件市场和插件侧边栏中显示。以下是设置插件图标的步骤: 准备…...

网络安全学习-NTFS安全权限、文件共享
NTFS安全权限 权限概述 设置NTFS权限,实现不同用户访问不同对象(文件、文件夹)的权限分配正确访问权限后,用户才能访问资源设置权限防止资源被篡改、删除 文件系统概述 文件系统就是这个分区的存储格式,不建立文件…...

如何使用GPT4写一篇综述
使用 GPT-4 或任何其他高级语言模型来撰写一篇综述文章,需要遵循一系列的步骤来确保内容的准确性、深度和组织性。以下是一些指导步骤: 确定主题和范围 明确你想要综述的主题。这可以是一个科学领域的特定方面、技术发展、理论进展等。 确定综述的范围和…...

【网络编程】基于UDP数据报实现回显服务器程序
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【网络编程】【Java系列】 本专栏旨在分享学习网络编程的一点学习心得,欢迎大家在评论区交流讨论💌 前言 我们如果…...
Jenkins自动化构建打包,部署
1.环境准备 上传jdk,maven和tomcat的包,解压到/usr/local下并配置环境变量。 配置jdk [rootserver04 ~]# vim /etc/profile.d/java.sh JAVA_HOME/usr/local/java export PATH$JAVA_HOME/bin:$PATH##加载环境变量 [rootserver04 ~]# source /etc/profi…...

python画图【00】Anaconda和Pycharm和jupyter的使用
①Anaconda ②Pycharm 一、Anaconda安装步骤 1、双击安装包,点击next。 2、点我同意I agree 3、 4、选择需要安装的位置,位置可根据自己情况安装到具体位置,但要记住安装到了哪里。然后点击next 5、可选择加入到环境变量,…...

【hive】Hive中的大宽表及其底层详细技术点
简介: 在大数据环境中,处理大规模数据集是常见的需求。为了满足这种需求,Hive引入了大宽表(Large Wide Table)的概念,它是一种在Hive中管理和处理大量列的数据表格。本文将详细介绍Hive中的大宽表概念以及其底层的详细…...

铁死亡调控机制新发现——癌症篇
随着癌细胞对凋亡产生抗性,非细胞凋亡死亡模式的铁死亡成为对抗治疗耐药癌症的新策略,对传统疗法产生耐药性的细胞或转移性癌细胞已被证明对铁死亡的敏感性增加。因此,靶向癌症中的铁死亡调控元件可能提供新的治疗机会。 今年5月来自德国维尔…...
MySQL 数据库系列课程 05:MySQL命令行工具的配置
一、Windows启动命令行工具 (1)打开 Windows 的开始菜单,找到安装好的 MySQL,点击MySQL 8.0 Command Line Client - Unicode,这个带有 Unicode 的,是支持中文的,允许在命令行中敲中文。 &…...

LeetCode 2703. 返回传递的参数的长度
请你编写一个函数 argumentsLength,返回传递给该函数的参数数量。 示例 1: 输入:args [5] 输出:1 解释: argumentsLength(5); // 1 只传递了一个值给函数,因此它应返回 1。 示例 2: 输入&a…...

MySQL的聚簇索引和非聚簇索引的区别以及示例
MySQL的聚簇索引和非聚簇索引 聚簇索引 聚簇索引是一种索引结构,它与数据行存储在一起,即索引的叶子节点就是数据行本身。在MySQL中,主键索引就是一种典型的聚簇索引。 涉及情况 当查询需要按照主键或唯一索引进行精确查找时,…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
