浮点数的转换--IEEE 754
IEEE754标准是一种浮点数表示标准,一般分为
- 单精度(32位的二进制数);
- 双精度(64位的二进制数)
根据国际标准IEEE754,任意一个二进制浮点数V可以表示为下面形式:
- V = (-1)^s *(1+M)* 2^(E-127)(单精度)
- V = (-1)^s *(1+M)* 2^(E-1023)(双精度)
其中,E为阶码位,M为尾数部分,S为符号位;
- M: 1<=M<2, 即M写成1.xxxxx形式;
- EEE 754规定,计算机内部保存M它的第一位总是1,因此可以只保存后面的xxxxxx部分。如1.001时,尾数001,需要读取时,再把第一位的1加上去。这样做可以节省1位有效数字;
- E:无符号整数,如果E为8位,其取值范围为0~255;若E为11位,取值范围为0~2047
- 科学计数法中,E可以是负数,因此,IEEE 754规定,E的真实值必须再减去一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023;
- e.g. 2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
- 特殊处理:
- E不全为0或1时,浮点数就采用上面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将有效数字M前加上第一位的1;
- E全为0时,浮点数的指数E等于1-127(或者1-1023),有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字;即:V = (-1)^s *(M)* 2^(1-127)
- E全为1时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);如果有效数字M不全为0,表示这个数不是一个数(NaN)
下面以32bits的浮点数为例子:
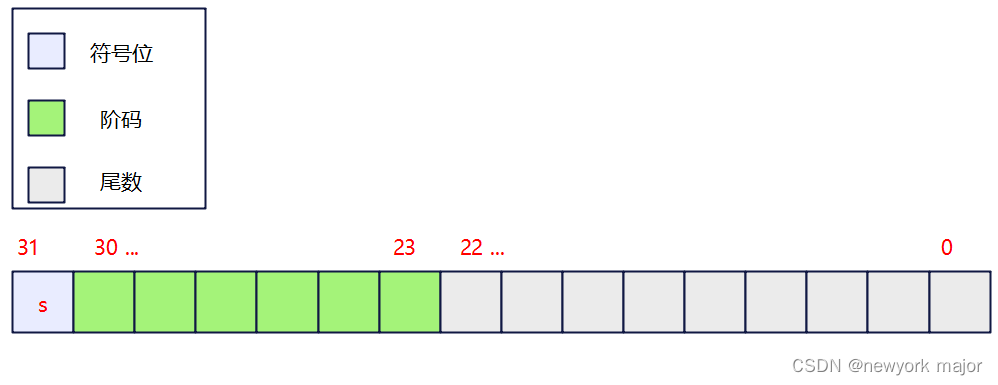
将十进制数0.15625转换为浮点数:
1. 将对应数据逐步乘以2,取整数部分;
⭘0.15625x2=0.3125 取整0
⭘0.31250x2=0.6250 取整0
⭘0.62500x2=1.2500 取整1
⭘0.25000x2=0.5000 取整0
⭘0.50000x2=1.0000 取整1
2. 将整数部分进行组合,得到0.00101;
3. 将得到的数,表示成IEEE 754的格式,0.00101=1.01*2-3
4. 将该数据,与公式进行对比,可以得出:1.01*2**-3 = (-1)s * (1+M)*2**(E-127), 可以得出:
⭘s=0;
⭘1+M=1.01, M=0.01;
⭘E-127=-3, E=124; 124 = BIN 0111 1100
5. 将上述的值,填入到32bits的范围内,可得:

使用上面的方式,转换十进制数-0.0625:
DEC -0.0625 = BIN -0.0001 = -1.0*2-4 s=1,M=1-1=0,E=-4 +127=123=0111 1011

使用上面的方式,转换十进制数127.1247:
这个数可能在32bits范围内,不能准确的表示出来,因此需要进行截位;
按照上面的公式,整数部分,127: 0111_1111;
小数部分:0.1247,不断乘以2,取整数部分,00011111111011001..., 因为位数不够,进行截断;
转换成上面的公式可以得到:M=1.11111100011111111011001,E=127+6=133, 所以转换后的浮点数为:
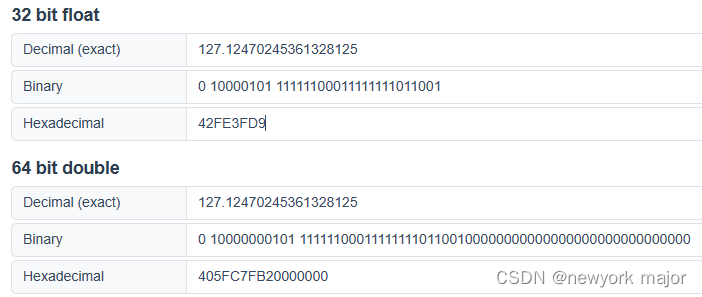
附上IEEE 754在线转换工具:
IEEE 754 浮点数 - 在线工具 (toolhelper.cn)
相关文章:

浮点数的转换--IEEE 754
IEEE754标准是一种浮点数表示标准,一般分为 单精度(32位的二进制数);双精度(64位的二进制数) 根据国际标准IEEE754,任意一个二进制浮点数V可以表示为下面形式: V (-1)^s *&#…...

若依框架介绍
RuoYi(若依)是一款基于Spring Boot、Spring Cloud等开源框架搭建的企业级开发平台,旨在提供全面的解决方案,简化企业级应用开发,提高开发效率。 主要特点: 1. 模块化设计 RuoYi采用模块化的设计࿰…...
iMazing2024免费版iOS移动设备管理软件
以自己的方式管理iPhone,让备受信赖的软件为您传输和保存音乐、消息、文件和数据。安全备份任何 iPhone、iPad 或 iPod touch。iMazing 功能强大、易于使用,称得上是 Mac 和 PC 上最好的 iOS 设备管理器。 正在为iTunes繁琐的操作发愁?设备数…...

Zookeeper整合Java实战,不同客户端使用汇总
Java学习面试指南:https://javaxiaobear.cn ZooKeeper应用的开发主要通过Java客户端API去连接和操作ZooKeeper集群。可供选择的Java客户端API有: ZooKeeper官方的Java客户端API。 第三方的Java客户端API,比如Curator。 ZooKeeper官方的客户…...

【python】Ubuntu下安装spyder及matplotlib中文显示
一、查看Ubuntu版本 $ lsb_release -a No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 22.04.3 LTS Release: 22.04 Codename: jammy尝试用cat /etc/debian_version命令,竟然可以显示出来Debian的版本。 $ cat /etc/debian_version …...

《运维人员的未来:IT界的“万金油“如何继续闪耀光芒》
文章目录 每日一句正能量前言35岁被称为运维半衰期,究竟为何?如何顺利过渡半衰期运维的职业发展路径后记 每日一句正能量 凡事顺其自然,遇事处于泰然,得意之时淡然,失意之时坦然,艰辛曲折必然,历…...
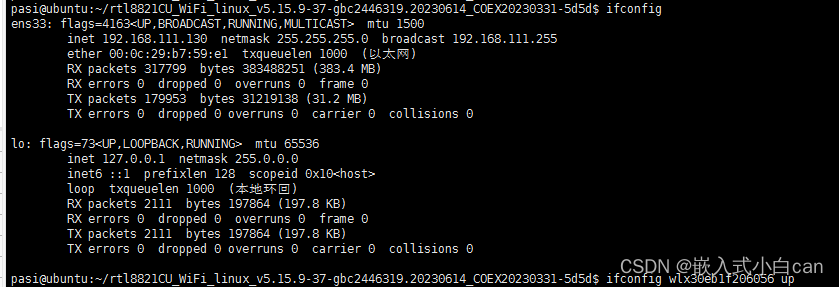
ip addr和ifconfig
ip addr可以显示更多信息,包括为启动的网络驱动如wlan,而ifocnfig只显示在线的驱动。若wlan是down的,则ip addr会显示信息,ifconfig不会显示信息。 ip addr: ifconfig:...

Crow:Middlewares 庖丁解牛7 after_handlers_call_helper
Crow:Middlewares 庖丁解牛6 middleware_call_helper-CSDN博客 介绍了对插件before_handle的调用 当完成了detail::middleware_call_helper的调用后,如果没有在before_handle中设置req被终止处理,也就是 if (!res.completed_) {need_to_call_after_handlers_ = true;handler…...

ts相关笔记(extends、infer、Pick、Omit)
最近刷了本ts小册,对一些知识点做下笔记。 extends extends 是一个关键字,用于对类型参数做一些约束。 A extends B 意味着 A 是 B 的子类型,比如下面是成立的 ‘abc’ extends string599 extends number 看下面例子: type …...
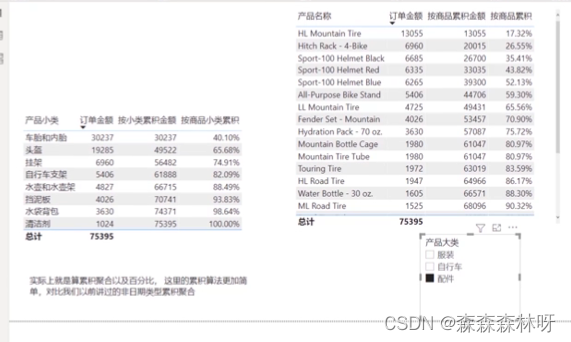
8.21 PowerBI系列之DAX函数专题-帕累托分析
需求 实现 1 按商品小类累积 var rollup_sales calculate(//计算当前累计销售额 [销售额], filter(allselected(order_2[产品小类]),sum(order_2[订单金额])<[销售额]) ) //按小类累积金额,filter内的销售额为选中的各小类的销售额 //金额从大到小累积,用&l…...

结构体-2-测试排名
22-结构体-2-测试排名 [命题人 : 外部导入] 时间限制 : 1.000 sec 内存限制 : 128 MB 题目描述 为了提升同学们的编程能力,老师们会在平时进行C语言的上机测试,了解班上同学的学习情况,对于一些测试成绩较差的同学,老师会进行督促…...

LeetCode刷题---快乐数
解题思路 该题的解题思路为使用哈希表来存储每次平方的和的结果,看是否有重复的数,如果存在第n次的平方和的数和第i次(i<n)平方和的数想等,那么它就不是一个快乐数。否则,则为快乐数。 代码实现: public boolean i…...

web前端游戏项目-辨色大比拼【附源码】
web前端游戏项目-辨色大比拼【附源码】 《辨色大比拼》是一个旨在测试和提升玩家颜色识别能力的在线游戏。在游戏中,玩家将通过辨识颜色来解谜并推进游戏进程。辨色大比拼也是一个寓教于乐的游戏,它不仅提供了一个有趣的辨色挑战,还能帮助玩…...

MongoDB操作_数据库_集合
.......................................................................................................................................................... 三、MongoDB操作 3.1 数据库操作 一个mongodb中可以建立多个数据库。 MongoDB的默认数据库为"test…...
50个免费的 AI 工具,提升工作效率(附网址)
上次我们已经介绍了20个精选的提高工作效率的免费AI工具,但如果你觉得这些AI工具还不过瘾的话,想进一步成为职场中最了解AI的人,本文将汇总介绍免费最新的50个AI工具。 DeepSwap DeepSwap 是一个基于 AI 的工具,适用于想要制作令人…...

g++ strip debug
strip(1) command_--strip-debug-CSDN博客 strip main.outll main.out -rwxr-xr-x 1 root root 6272 Mar 22 16:14 main.outfile main.out main.out: ELF 64-bit LSB executable, x86-64, version 1 (SYSV), dynamically linked (uses shared libs), for GNU/Linux 2.6.32, Bu…...

微服务实战系列之Dubbo(上)
前言 随着一年一度冬至的到来,2023的步伐也将远去。而博主的系列文章,也将从今天起,越来越聚焦如何构建微服务“内核”上。前序系列文章几乎囊括了微服务的方方面面,无论使用什么框架、组件或工具,皆可拿来用之。 那么…...

一篇讲透:箭头函数、普通函数有什么区别
前言 📫 大家好,我是南木元元,热衷分享有趣实用的文章,希望大家多多支持,一起进步! 🍅 个人主页:南木元元 目录 什么是箭头函数 箭头函数和普通函数的区别 更简洁的语法 箭头函数…...

第40节: Vue3 注册生命周期钩子
在UniApp中使用Vue3框架时,你可以注册生命周期钩子来执行特定的逻辑。以下是一个示例,演示了如何在UniApp中使用Vue3框架注册生命周期钩子: <template> <view> <p>{{ message }}</p> </view> </templ…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

