矩阵理论基本知识
1、矩阵范数、算子范数
- 矩阵无穷范数是非自相容范数,矩阵1-范数、矩阵2-范数是自相容范数
- 矩阵2-范数:Frobenius范数,是向量2-范数的自然推广。 ∥ A ∥ m 2 = ∥ A ∥ F = ∑ a i j ∗ a i j \|A\|_{m2}=\|A\|_{F}=\sqrt{\sum a_{ij}^*a_{ij}} ∥A∥m2=∥A∥F=∑aij∗aij
- ∥ A ∥ m 2 = t r ( A H A ) = A 的正奇异值的平方和 \|A\|_{m2} = \sqrt{tr(A^HA)} = \sqrt{A的正奇异值的平方和} ∥A∥m2=tr(AHA)=A的正奇异值的平方和
- ∥ A ∥ m 2 = ∥ U H A V ∥ m 2 = ∥ U A V H ∥ m 2 \|A\|_{m2} = \|U^HAV\|_{m2}=\|UAV^H\|_{m2} ∥A∥m2=∥UHAV∥m2=∥UAVH∥m2
- ∥ A ∥ m 2 = ∥ U A ∥ m 2 = ∥ A V ∥ m 2 = ∥ U A V ∥ m 2 \|A\|_{m2} = \|UA\|_{m2}=\|AV\|_{m2} = \|UAV\|_{m2} ∥A∥m2=∥UA∥m2=∥AV∥m2=∥UAV∥m2
- 矩阵范数是相容范数:则必存在向量范数与之相容。 ∣ ∣ A x ∣ ∣ ≤ ∣ ∣ A ∣ ∣ m ∣ ∣ x ∣ ∣ ||Ax||\le||A||_m ||x|| ∣∣Ax∣∣≤∣∣A∣∣m∣∣x∣∣
- 证明过程:构造 ∣ ∣ x ∣ ∣ = ∣ ∣ x a H ∣ ∣ m ||x|| = ||xa^H||_m ∣∣x∣∣=∣∣xaH∣∣m
- 矩阵的特征值一定小于等于该矩阵范数。
- 反过来说,如果矩阵的特征值大于了某个矩阵范数,则该矩阵范数一定不相容。
- 任意向量范数:则必存在矩阵范数与之相容,其中放大效果的最大值称为算子范数。
- 算子范数再大,不过向量范数的上确界,鸡头始终是鸡
- 和向量范数相容的矩阵范数,终归是矩阵范数,始终有 ∣ ∣ A x ∣ ∣ ≤ ∣ ∣ A ∣ ∣ m ∣ ∣ x ∣ ∣ ||Ax||\le||A||_m ||x|| ∣∣Ax∣∣≤∣∣A∣∣m∣∣x∣∣,所以矩阵范数会大于算子范数。
- 换句话说,和向量范数相容的矩阵范数的下确界是算子范数。
- 算子范数是自相容矩阵范数。 ∣ ∣ A k ∣ ∣ ≤ ∣ ∣ A ∣ ∣ k ||A^k||\le ||A||^k ∣∣Ak∣∣≤∣∣A∣∣k
- 常见算子范数:
- 从属于向量1-范数的算子范数称为算子1范数:极大绝对列和范数;
- 从属于向量2-范数的算子范数称为算子2范数:谱范数= r ( A H A ) \sqrt{r(A^HA)} r(AHA);
- 从属于向量∞-范数的算子范数称为算子无穷范数:极大绝对行和范数;
- 证明思路:存在上界,上界可达。
- 算子范数的性质: ∣ ∣ ⋅ ∣ ∣ ||\cdot|| ∣∣⋅∣∣是算子范数
- ∣ ∣ E ∣ ∣ = 1 ||E||=1 ∣∣E∣∣=1
- ∣ ∣ A − 1 ∣ ∣ ≥ ∣ ∣ A ∣ ∣ − 1 ||A^{-1}||\ge ||A||^{-1} ∣∣A−1∣∣≥∣∣A∣∣−1; ∣ ∣ A ∣ ∣ ≥ ∣ ∣ A − 1 ∣ ∣ − 1 ||A||\ge ||A^{-1}||^{-1} ∣∣A∣∣≥∣∣A−1∣∣−1
- ∣ ∣ A − 1 ∣ ∣ − 1 = inf ∣ ∣ A x ∣ ∣ ∣ ∣ x ∣ ∣ = m i n x ≠ 0 ∣ ∣ A x ∣ ∣ ∣ ∣ x ∣ ∣ ≤ ∣ ∣ A ∣ ∣ ||A^{-1}||^{-1} = \inf \frac{||Ax||}{||x||} = min_{x\ne0} \frac{||Ax||}{||x||}\le||A|| ∣∣A−1∣∣−1=inf∣∣x∣∣∣∣Ax∣∣=minx=0∣∣x∣∣∣∣Ax∣∣≤∣∣A∣∣
- ∣ λ ∣ ≤ ∣ ∣ A ∣ ∣ |\lambda|\le ||A|| ∣λ∣≤∣∣A∣∣; ∣ λ k ∣ ≤ ∣ ∣ A k ∣ ∣ |\lambda^k|\le ||A^k|| ∣λk∣≤∣∣Ak∣∣
- HÖlder 范数:p-范数。可以p取1和无穷。
- HÖlder不等式: ∣ X H Y ∣ ≤ ∑ ∣ x i ∣ ∣ y j ∣ ≤ ∥ X ∥ q ∥ Y ∥ p , 1 / q + 1 / p = 1 |X^HY|\le \sum|x_i||y_j| \le\|X\|_q\|Y\|_p, 1/q+1/p=1 ∣XHY∣≤∑∣xi∣∣yj∣≤∥X∥q∥Y∥p,1/q+1/p=1
2、矩阵分解
已经写过一期了,见:矩阵理论–矩阵分解
补充:
正规矩阵A性质: A H A = A A H A^HA=AA^H AHA=AAH
- λ ( A ) = λ ˉ ( A H ) \lambda(A)=\bar \lambda(A^H) λ(A)=λˉ(AH); ∣ ∣ A x ∣ ∣ = ∣ ∣ A H x ∣ ∣ ||Ax|| = ||A^Hx|| ∣∣Ax∣∣=∣∣AHx∣∣
- A的特征子空间和AH的特征子空间完全相同。
- A的特征子空间正交。不同特征值的特征向量必正交。
- A是单纯矩阵
任意矩阵A:
- ∥ A ∥ m 2 = t r ( A H A ) = t r ( A A H ) \|A\|_{m2} = \sqrt{tr(A^HA)} = \sqrt{tr(AA^H)} ∥A∥m2=tr(AHA)=tr(AAH)
- A H A A^HA AHA和 A A H AA^H AAH的非零特征值完全相同,数值相同、代数重复度相同。
- rank(A)=rank(AH)=rank(AHA)=rank(AAH)。证明很重要
- AHA的核空间包含A的核空间,即Ax=0,则必有AHAx=0
- A的核空间包含AHA的核空间,即AHAx=0,则必有xHAHAx=<Ax,Ax>=0,即Ax=0
- N(AHAx)=N(A),由秩-零化度定理知:rank(A)=rank(AHA)
- A H A A^HA AHA和 A A H AA^H AAH都是半正定矩阵。
- A的特征值和奇异值的关系:
- 若A为非方阵,则A没有特征值。但A有奇异值。
- 如果A为方阵,则A的特征值的平方和<=A的奇异值的平方和。
- 如果A为正规矩阵,则A的特征值的平方和==A的奇异值的平方和。
- 因为正规矩阵酉相似于对角阵,任意方阵酉相似于三角阵。
3、矩阵的估计
1、有关特征值的不等式
- 舒尔不等式: ∑ i = 1 n ∣ λ i ∣ 2 ≤ ∣ ∣ A ∣ ∣ F 2 \sum_{i=1}^{n}|\lambda_i|^2 \le ||A||_F^2 ∑i=1n∣λi∣2≤∣∣A∣∣F2
- Hirsh不等式: ∣ λ i ∣ ≤ n ∣ ∣ A ∣ ∣ m ∞ |\lambda_i| \le n ||A||_{m_\infty} ∣λi∣≤n∣∣A∣∣m∞
- Bendixson不等式: ∣ I m λ i ∣ ≤ n ( n − 1 ) 2 ∣ ∣ ( A − A H ) / 2 ∣ ∣ m ∞ , A ∈ R n × n |Im\lambda_i|\le \sqrt{\frac{n(n-1)}{2}}||(A-A^H)/2||_{m_\infty},A\in R^{n\times n} ∣Imλi∣≤2n(n−1)∣∣(A−AH)/2∣∣m∞,A∈Rn×n
- n(n-1)是因为实矩阵的反共轭对称分量是的对角元为0。
- 除以2是因为实矩阵的复特征根成对出现。
- 其余证明同Hirsh不等式
- Browne不等式: σ n ≤ ∣ λ i ∣ ≤ σ 1 \sigma_n\le|\lambda_i|\le \sigma_1 σn≤∣λi∣≤σ1
- Hadamard不等式: ∏ i = 1 n ∣ λ i ∣ = ∣ det ( A ) ∣ ≤ ∏ i = 1 n α i H α i \prod_{i=1}^{n}|\lambda_i|=|\det(A)|\le \sqrt{\prod_{i=1}^n\alpha_i^H\alpha_i} ∏i=1n∣λi∣=∣det(A)∣≤∏i=1nαiHαi
- 施密特正交化:A = BR,R是单位正线上三角
- det ( A ) = det ( B R ) = det ( B ) det ( R ) = det ( B ) \det(A) = \det(BR)=\det(B)\det(R)=\det(B) det(A)=det(BR)=det(B)det(R)=det(B)
- $|\det(B)|^2 = |\det(B^H)\det(B)| = |\det(BHB)|=\prod_{i=1}n b_i^Hb_i \le\prod_{i=1}^n \alpha_i^H\alpha_i $
- ∣ det ( A ) ∣ ≤ ∏ i = 1 n α i H α i |\det(A)|\le \sqrt{\prod_{i=1}^n\alpha_i^H\alpha_i} ∣det(A)∣≤∏i=1nαiHαi
2、盖尔圆盘定理
- 关于圆盘定理1、圆盘定理2:Gerschgorin定理,以及用python绘制Gerschgorin圆盘动图
- 有的盖尔圆里面可能没有特征值(盖尔圆盘连通,将导致特征值函数不连续)
- n阶矩阵A的n个圆盘均孤立,则A可对角化(充分不必要)。
- n阶实矩阵A的n个圆盘均孤立,则A的特征根均为实数。
- 行严格对角占优矩阵A:
- 若A的对角元全大于0,则A的所有特征值有正实部;
- 若A的对角元全大于0,且A是Hermite矩阵,那么A的所有特征值均为正数。
3、Hermite矩阵的变分特征
-
Courant-Fischer定理:Hermite矩阵的特征值估计——courant-fischer定理
-
Weyl定理(韦尔定理):
- A,B均为Hermite矩阵
- λ k ( A ) + λ n ( B ) ≤ λ k ( A + B ) ≤ λ k ( A ) + λ 1 ( B ) \lambda_k(A)+\lambda_n(B)\le\lambda_k(A+B)\le\lambda_k(A)+\lambda_1(B) λk(A)+λn(B)≤λk(A+B)≤λk(A)+λ1(B)
4、矩阵分析
-
矩阵序列极限的运算规则:A(k)、B(k)的极限为A、B
- 线性运算:aA(k)+bB(k) →aA+bB (k → +∞)
- 乘:A(k)B(k) →AB (k → +∞)
- 当A(k)、A均可逆的时候:(A(k))-1 → A-1 (k → +∞)
-
用矩阵范数定义矩阵序列极限:
- lim k → + ∞ ∣ ∣ A ( k ) − A ∣ ∣ = 0 \lim_{k\to+\infty}||A^{(k)}-A||=0 limk→+∞∣∣A(k)−A∣∣=0
-
收敛矩阵 等价于 谱半径r(A)<1
- lim k → + ∞ A k = O \lim_{k\to+\infty}A^k=O limk→+∞Ak=O称为收敛矩阵
-
矩阵级数绝对收敛的充要条件是正项级数 ∑ i = 0 ∞ ∣ ∣ A ( k ) ∣ ∣ \sum_{i=0}^{\infty}||A^{(k)}|| ∑i=0∞∣∣A(k)∣∣收敛
-
Neumann级数:E+A+A2+A3+…… = (E-A)-1. r(A)<1时成立
-
矩阵幂级数f(A):数项幂级数f(z)收敛半径为r,若r(A)<r则f(A)绝对收敛
-
矩阵函数:收敛的矩阵幂级数的和S,记作f(A)
-
收敛半径判断方法:
- 达朗贝尔判敛法: lim n → ∞ ∣ c n + 1 c n ∣ = ρ {\displaystyle \lim _{n\to \infty }\left\vert {c_{n+1} \over c_{n}}\right\vert =\rho } n→∞lim cncn+1 =ρ , R = 1/rho
- 柯西判敛法: R = lim inf n → ∞ ∣ c n ∣ − 1 n {\displaystyle R=\liminf _{n\to \infty }\left|c_{n}\right|^{-{\frac {1}{n}}}} R=n→∞liminf∣cn∣−n1
-
四阶Jordan块的k次幂,特征值为a: [ a k k a k − 1 k ( k − 1 ) 2 ! k k − 2 k ( k − 1 ) ( k − 2 ) 3 ! k k − 3 0 a k k a k − 1 k ( k − 1 ) 2 ! k k − 2 0 0 a k k a k − 1 0 0 0 a k ] \begin{bmatrix}a^k&ka^{k-1}&\frac{k(k-1)}{2!}k^{k-2}&\frac{k(k-1)(k-2)}{3!}k^{k-3} \\0&a^k&ka^{k-1}&\frac{k(k-1)}{2!}k^{k-2}\\0&0 &a^k&ka^{k-1}\\0&0&0&a^k\end{bmatrix} ak000kak−1ak002!k(k−1)kk−2kak−1ak03!k(k−1)(k−2)kk−32!k(k−1)kk−2kak−1ak
5、广义逆矩阵
逆,生来就是用于解方程组的。
-
逆:行列满秩。
-
单边逆:左逆列满秩;右逆行满秩。
-
求法:高斯消元。
-
列满秩矩阵:Ax=b
- 行初等变换,可以得到左逆 A L − 1 A_L^{-1} AL−1。
- 有解的充要条件: A A L − 1 b = b AA_L^{-1}b=b AAL−1b=b
- 唯一解: x = ( A H A ) − 1 A H b = A L − 1 b \Large x = (A^HA)^{-1}A^Hb=A_L^{-1}b x=(AHA)−1AHb=AL−1b
- 需要注意,左逆矩阵不唯一, ( A H A ) − 1 A H (A^HA)^{-1}A^H (AHA)−1AH也是列满秩矩阵A的左逆。
-
行满秩矩阵:
- 列初等变换,可以得到右逆 A R − 1 A_R^{-1} AR−1。
- 行满秩矩阵一定有解,且解不唯一。自由未知数的个数为n-m
- A H ( A A H ) − 1 A^H(AA^H)^{-1} AH(AAH)−1是A的一个右逆。右逆矩阵不唯一。
- 需要注意: A H ( A A H ) − 1 b ≠ A R − 1 b \large A^H(AA^H)^{-1}b {\ne} A_R^{-1}b AH(AAH)−1b=AR−1b 通常情况求出来的是两个不同的解,均满足Ax=b。这是因为行满秩矩阵Ax=b的解不唯一。
- 行满秩矩阵的A+是A的一个右逆。
-
-
广义逆:任何矩阵都存在广义逆矩阵。
-
AGA=A 等价于 G是A的广义逆矩阵
-
单边逆是广义逆的特殊情况。
-
Ax = b有解的充要条件:rank A = rank (A b)
-
当A列满秩,且rank A = rank (A b) ,则有唯一解。
-
当A非列满秩,且有解,则有无穷多解。
-
Gb = x , 且Ax = b,则称G是A的一个广义逆。
-
广义逆矩阵不唯一,零矩阵的广义逆矩阵是任意矩阵。
-
广义逆矩阵通常记作 A − A^- A−,区别于 A − 1 A^{-1} A−1
-
广义逆矩阵的秩 大于等于 A的秩。
-
广义逆矩阵是逆矩阵的推广,当A是可逆矩阵的时候,A-=A-1
-
广义逆矩阵有逆矩阵类似的性质:
性质 广义逆矩阵 逆矩阵 定义 对于矩阵A,存在矩阵B,使得ABA=A 对于方阵A,存在矩阵B,使得AB=BA=I 记号 A − A^- A− A − 1 A^{-1} A−1 行为 对于任意向量b,满足 A A − AA^- AA−b=b 对于任意向量b,满足 A A − 1 AA^{-1} AA−1b=b 矩阵乘法 A A − AA^- AA−A=A AA − 1 ^{-1} −1A=A 矩阵的秩 rank( A − A A^-A A−A)=rank( A A − AA^- AA−)=rank(A) rank(AA − 1 ^{-1} −1)=rank(A)=n(满秩) 逆的存在 广义逆存在于可逆和不可逆矩阵中 逆存在于方阵(可逆矩阵)中 唯一性 广义逆可以有多个不同的解 逆是唯一的 幂等性 A A − AA^- AA− 、 A − A A^-A A−A是幂等矩阵 A A − 1 = A − 1 A = I AA^{-1}=A^{-1}A=I AA−1=A−1A=I是幂等矩阵 数乘 aA的广义逆为 1 a A − , a ≠ 0 \frac{1}{a} A^-,a\ne0 a1A−,a=0 aA的逆为 1 a A − 1 , a ≠ 0 \frac{1}{a} A^{-1},a\ne0 a1A−1,a=0 正交投影 若 ( A A − ) H = A A − (AA^-)^H=AA^- (AA−)H=AA−,则 A A − = P R ( A ) AA^-=P_{R(A)} AA−=PR(A) A A − 1 = I AA^{-1}=I AA−1=I,I是从Cn到R(A)的正交投影
-
-
自反广义逆
- 定义:AGA=A且GAG=G。存在且不唯一。
- 求法:
- 最大秩分解法:A=BD, A r − = D R − 1 B L − 1 A_r^-=D_R^{-1}B_L^{-1} Ar−=DR−1BL−1
- 构造法:X、Y是A的广义逆,则Z = XAY是自反广义逆,当然YAX也是自反广义逆。
- 公式法:X=(AHA)-AH,Y =AH(AAH)-都是自反广义逆
- R(AH)=R(AHA), N(A)=N(AHA)
- 存在D,使得AH=AHAD
- 代入可证明AXA=A
- rank(X)<=rank(AH)=rank(AHA) = rank(AHA(AHA)-AHA)=rank(AHAXA)<=rank(X)
- 所以X是自反广义逆
- A_是自反广义逆的充要条件是rank(A)=rank(A-)
- 必要性:AGA=A且GAG=G,则rank(A)=rank(AGA)<=rank(G)=rank(GAG)<=rank(A)
- 充分性:
- R(GA)属于R(G),R(GA)=R(A)=R(G),则R(G)=R(GA);
- GE=G,则存在X,GAX=G
- A=AGA=AGAXA=AXA
- 由构造法知G是自反广义逆
- 几何性质
- R ( A ) ⊕ N ( A H ) = C m R(A)\oplus N(A^H)=C^m R(A)⊕N(AH)=Cm
- R ( A H ) ⊕ N ( A ) = C n R(A^H)\oplus N(A)=C^n R(AH)⊕N(A)=Cn
- R ( A ) ⊕ N ( A r − ) = C m R(A)\oplus N(A^-_r)=C^m R(A)⊕N(Ar−)=Cm
- R ( A r − ) ⊕ N ( A ) = C n R(A^-_r)\oplus N(A)=C^n R(Ar−)⊕N(A)=Cn
- R ( A r − ) = R ( A H ) R(A^-_r) = R(A^H) R(Ar−)=R(AH)
- N ( A r − ) = N ( A H ) N(A^-_r) = N(A^H) N(Ar−)=N(AH)
-
MP广义逆
- 定义:AGA=A,GAG=G,(GA)H=GA, (AG)H=AG
- 存在且唯一
- 计算方法:
- 最大值分解法: A + = D H ( D D H ) − 1 ( B H B ) − 1 B H A^+=D^H(DD^H)^{-1}(B^HB)^{-1}B^H A+=DH(DDH)−1(BHB)−1BH
- 奇异值分解法: A + = V H D + U H A^+=V^HD^+U^H A+=VHD+UH
- 注意:最大值分解不唯一,然而最大值分解的这种乘积,即A+是唯一的。
- A+的性质:
- 自反性:(A+)+=A
- 唯一性: A + = ( A H A ) + A H = A H ( A A H ) + = D H ( D D H ) − 1 ( B H B ) − 1 B H A^+=(A^HA)^+A^H=A^H(AA^H)^+=D^H(DD^H)^{-1}(B^HB)^{-1}B^H A+=(AHA)+AH=AH(AAH)+=DH(DDH)−1(BHB)−1BH
- 几何性质: R ( A + ) = R ( A H ) R(A^+) = R(A^H) R(A+)=R(AH)
- 正交投影性: A A + = P R ( A ) , A + A = P R ( A H ) AA^+=P_{R(A)},A^+A=P_{R(A^H)} AA+=PR(A),A+A=PR(AH)
- 行列子空间相等性:R(A)=R(AH)的充要条件是 A + A = A + A A^+A=A^+A A+A=A+A
- ( A H A ) + = A + ( A H ) + = A + ( A A H ) + A = A H ( A A H ) + ( A H ) + (A^HA)^+=A^+(A^H)^+=A^+(AA^H)^+A=A^H(AA^H)^+(A^H)^+ (AHA)+=A+(AH)+=A+(AAH)+A=AH(AAH)+(AH)+
- A + A = ( A H A ) + ( A H A ) = ( A H A ) ( A H A ) + A^+A=(A^HA)^+(A^HA)=(A^HA)(A^HA)^+ A+A=(AHA)+(AHA)=(AHA)(AHA)+
- 若A是Hermite矩阵:
- ( A 2 ) + = ( A + ) 2 (A^2)^+=(A^+)^2 (A2)+=(A+)2
-
矩阵方程通解:
- AXB=D有解的充要条件:AA-DB-B=D
- 通解:X=A-DB-+Y-A-AYBB-
- Ax=b有解的充要条件:AA-b=b
- 通解:x = AA-b +y-A-1Ay
-
相容方程组的最小范数解:
- 相容方程组:有解方程组
- AGA=A,(GA)H=GA
- Gb=x是最小范数解
-
不相容方程组的最小二乘解:
- 不相容方程组:无解方程组
- AGA=A,(AG)H=AG
- Gb=x是最小二乘解
-
不相容方程组的最小二乘解有时候不够好,最小二乘解的最小范数解叫最佳逼近解:
- 最佳逼近解:A+b=x
- 如果方程组是相容方程组,则A+b是最小范数解
-
关于广义逆的运算规则
- ( A − ) H = ( A H ) − (A^-)^H=(A^H)^- (A−)H=(AH)−
- B = S A T , B − = T − 1 A − S − 1 B=SAT,B^-=T^{-1}A^-S^{-1} B=SAT,B−=T−1A−S−1
- ( A B ) + = B + A + (AB)^+=B^+A^+ (AB)+=B+A+的充要条件: R ( A H A B ) ⊂ R ( B ) , R ( B B H A H ) ⊂ R ( A H ) R(A^HAB)\sub R(B),R(BB^HA^H)\sub R(A^H) R(AHAB)⊂R(B),R(BBHAH)⊂R(AH)
相关文章:

矩阵理论基本知识
1、矩阵范数、算子范数 矩阵无穷范数是非自相容范数,矩阵1-范数、矩阵2-范数是自相容范数矩阵2-范数:Frobenius范数,是向量2-范数的自然推广。 ∥ A ∥ m 2 ∥ A ∥ F ∑ a i j ∗ a i j \|A\|_{m2}\|A\|_{F}\sqrt{\sum a_{ij}^*a_{ij}} ∥…...

《深入理解Java虚拟机(第三版)》读书笔记:Java内存区域与内存溢出异常、垃圾收集器与内存分配策略
下文是阅读《深入理解Java虚拟机(第3版)》这本书的读书笔记,如有侵权,请联系删除。 文章目录 第2章 Java内存区域与内存溢出异常2.2 运行时数据区域2.3 HotSpot虚拟机对象探秘 第3章 垃圾收集器与内存分配策略3.2 对象已死&…...

android 手机主界面侧滑退出app问题
最近重新搭了个app,发现手机显示APP主界面时,沿着手机右边向左滑,会直接关闭应用,所以想搞个第一次提示,第二次退出app的效果。 结果搞出个复杂的东西,下面是两段代码。1: 1:GestureDetector扩展函数。其…...

spring boot 配置全局日期和时间格式
spring boot 为项目配置 全局日期和时间格式化yyyy-MM-dd HH:mm:ss 方式一:代码配置全局日期和时间格式化 /*** author hua*/ Configuration public class WebConfiguration implements WebMvcConfigurer {/*** 项目全局时间格式化*/ Bean public ObjectMapper get…...
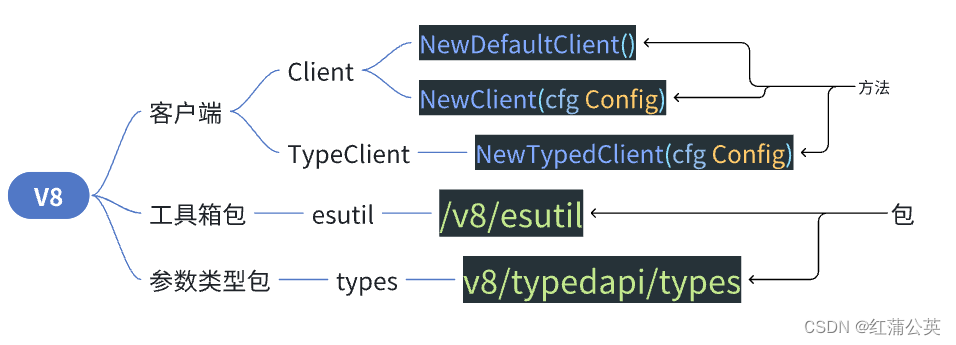
GoLang学习之路,对Elasticsearch的使用,一文足以(包括泛型使用思想)(二)
书写上回,上回讲到,Elasticsearch的使用前提即:语法,表结构,使用类型结构等。要学这个必须要看前面这个:GoLang学习之路,对Elasticsearch的使用,一文足以(包括泛型使用思…...
鸿蒙APP的代码规范
鸿蒙APP的代码规范是为了确保代码质量、可读性和可维护性而定义的一系列规则和标准。以下是一些建议的鸿蒙APP代码规范,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作。 1. 代码风格: 采用…...

蓝桥杯-每日刷题-027
出租汽车计费器 一、题目要求 题目描述 有一个城市出租汽车的计费规则是3公里内(含3公里)基本费6元,超过3公里,每一公里1.4元。 现在对于输入具体的公里数x(0<x<1000),编程计算x公里所需…...
安装Node修改Node镜像地址搭建Vue脚手架创建Vue项目
1、安装VSCode和Node 下载VSCode Visual Studio Code - Code Editing. Redefined 下载Node Node.js (nodejs.org) 检验是否安装成功,WinR,输入cmd命令,使用node -v可以查看到其版本号 2、修改镜像地址 安装好node之后,开始修改镜像地址 …...

git 学习 之一个规范的 commit 如何写
最好的话做一件完整的事情就提交一次...

2023 年人工智能研究与技术排名前 10 的国家
人工智能研究是一项全球性的工作。虽然美国和中国因其对人工智能的贡献而备受关注,但事实是,世界各国都在涉足这项技术,尝试新的突破,并吸引投资者的关注。 斯坦福大学的《2023年人工智能报告》估计,到 2022 年&#…...
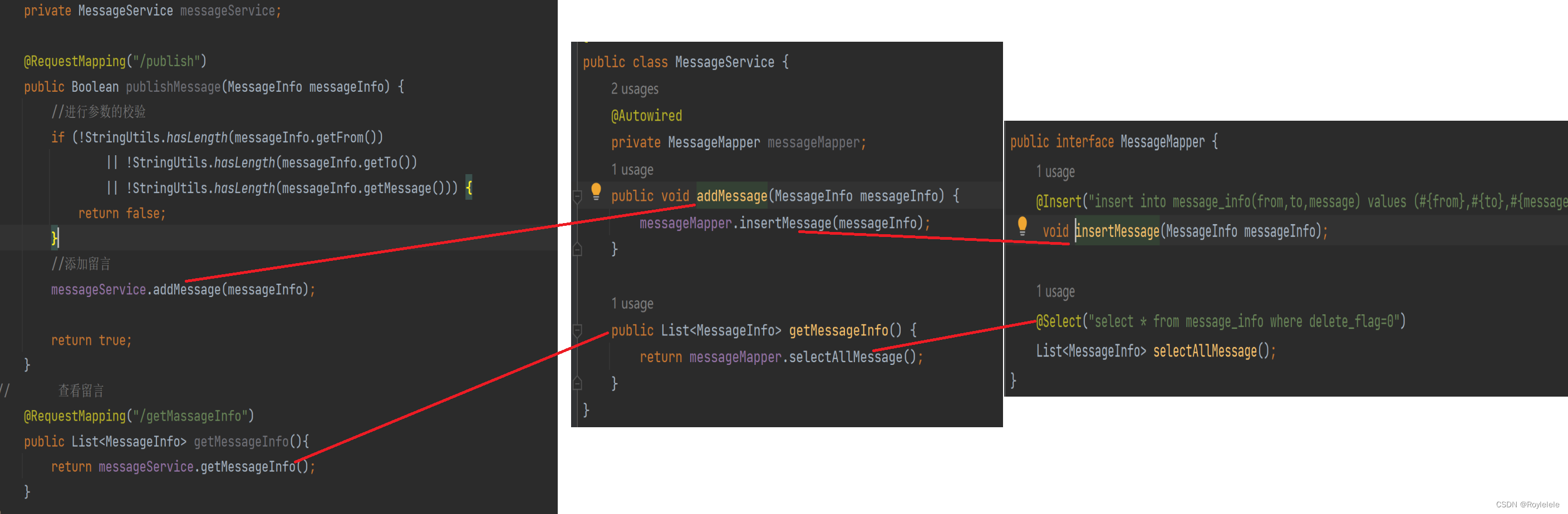
留言板(Mybatis连接数据库版)
目录 1.添加Mybatis和SQL的依赖 2.建立数据库和需要的表 3.对应表中的字段,补充Java对象 4.对代码进行逻辑分层 5.后端逻辑代码 之前的项目实例【基于Spring MVC的前后端交互案例及应用分层的实现】https://blog.csdn.net/weixin_67793092/article/details/134…...

第十二章 Sleuth分布式请求链路跟踪
Sleuth分布式请求链路跟踪 gitee:springcloud_study: springcloud:服务集群、注册中心、配置中心(热更新)、服务网关(校验、路由、负载均衡)、分布式缓存、分布式搜索、消息队列(异步通信)、数…...

EasyExcel多线程批量导出数据,动态表头,静态资源访问
1.导入依赖 <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.1.1</version></dependency>2.建立实体 Data public class ActResultLogVO implements Serializable {private static…...
树莓派界面改成中文
安装完树莓派系统(Raspberry Pi OS with Desktop),第一次启动时,时会有如下面二个图所示,让你选择区域时区和语言。 树莓派默认的语言为英文,如果你在安装时没有选择的话,默认的区域为英国,语言为英国英文&…...
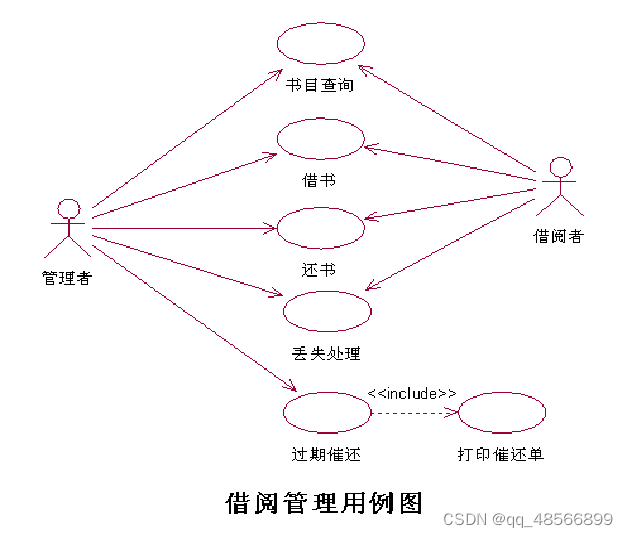
软件工程期末复习
● 用例:借书 ●参与者:管理员,借阅者 ●操作流: ① 管理员进入图书借阅界面,用例开始。 ② 系统要求输入借阅者的借书证编码。 ③系统检验借书证编码,如果正确,则显示借阅者的信息。 A1:借书证编码有错。 A2: 如果该借…...

【linux】select实现定时器
/*秒级定时器*/ void seconds_sleep(unsigned long seconds) {if(seconds 0) return;struct timeval tv;tv.tv_secseconds;tv.tv_usec0;int err;do{errselect(0,NULL,NULL,NULL,&tv);}while(err<0 && errnoEINTR); }/*毫秒定时器*/void milliseconds_slee…...
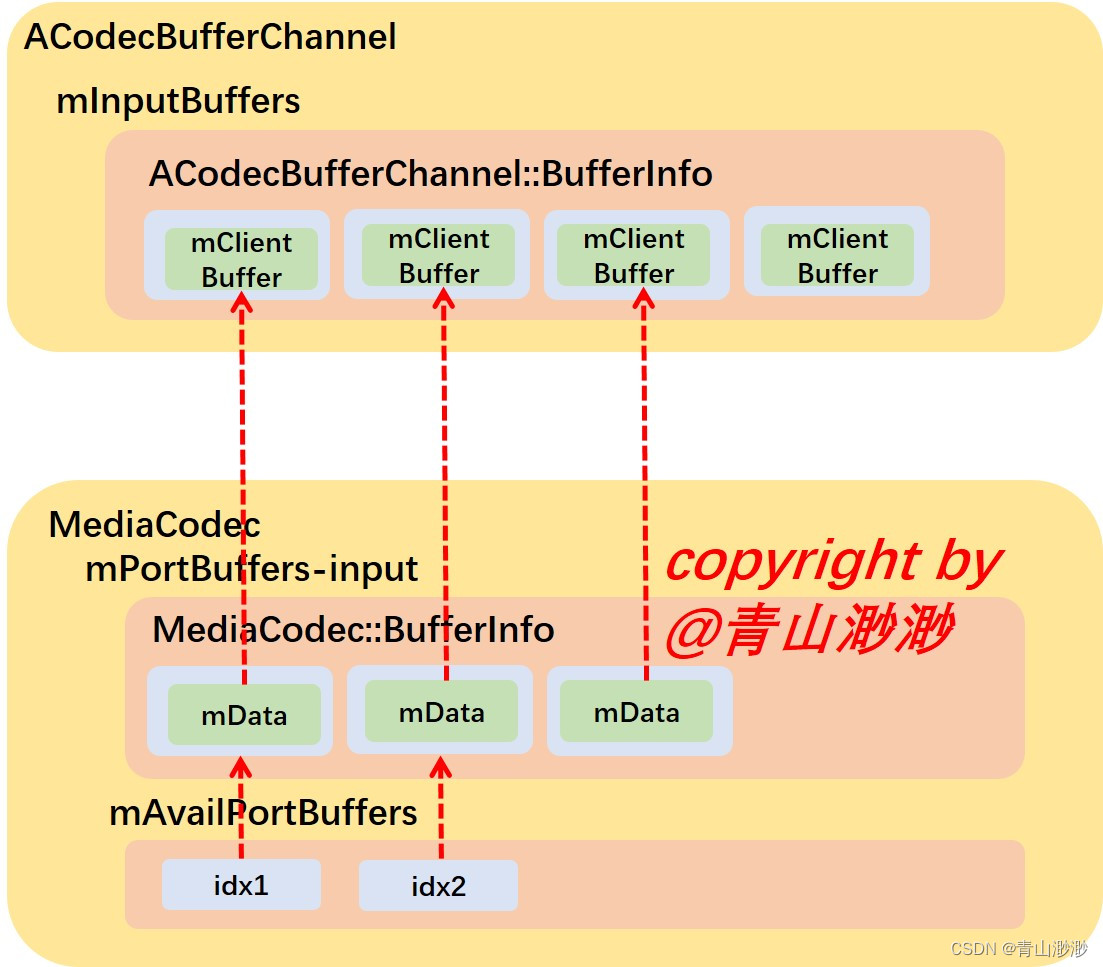
Android 13 - Media框架(28)- MediaCodec(三)
上一节我们了解到 ACodec 执行完 start 流程后,会把所有的 input buffer 都提交给 MediaCodec 层,MediaCodec 是如何处理传上来的 buffer 呢?这一节我们就来了解一下这部分内容。 1、ACodecBufferChannel::fillThisBuffer ACodec 通过调用 A…...
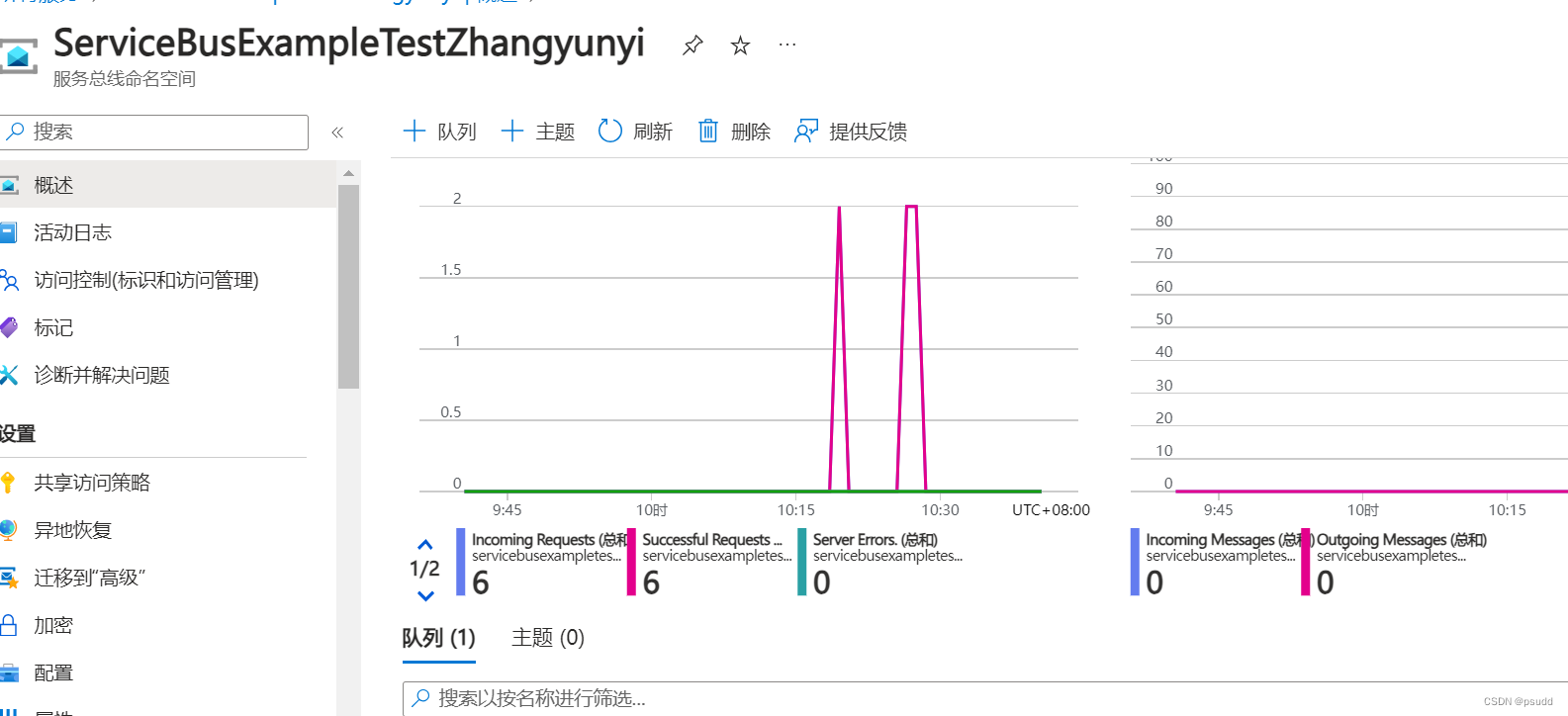
Azure 学习总结
文章目录 1. Azure Function1.1 Azure Function 概念1.2 Azure Function 实现原理1.3 Azure Function 本地调试1.4 Azure Function 云部署 2. Azure API Managment 概念 以及使用2.1 Azure API 概念2.2 Azure API 基本使用 3. Service Bus 应用场景及相关特性3.1 Service Bus 基…...

数据库是否可以直接作为数据仓库的数据源
在数据仓库使用数据时,我们是否可以直接将数据库作为数据源?如果使用了,会存在哪些问题? 数据库中存储的是业务数据,存储方式是行式存储;而数据仓库中数据是以列式存储的;如果数据仓库要想使用…...
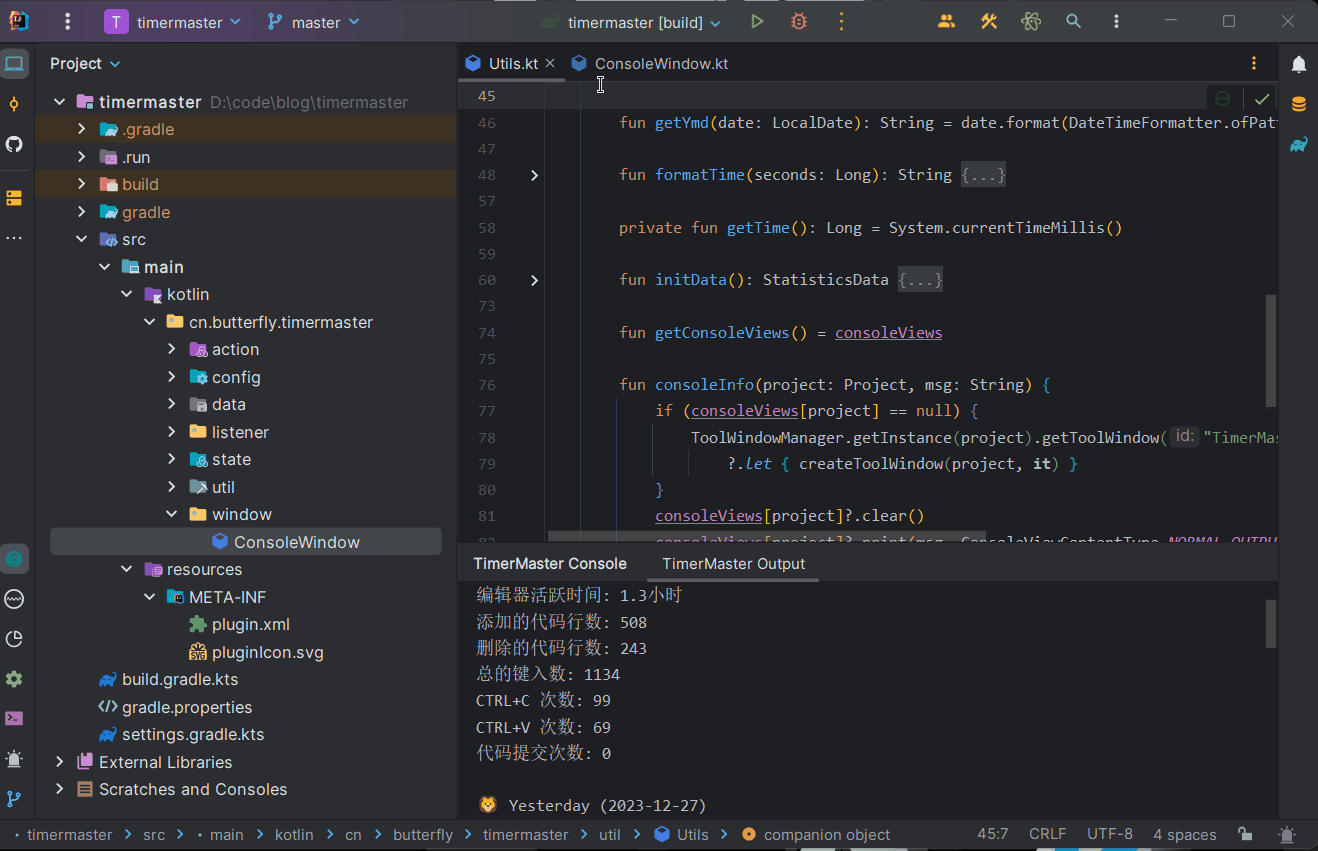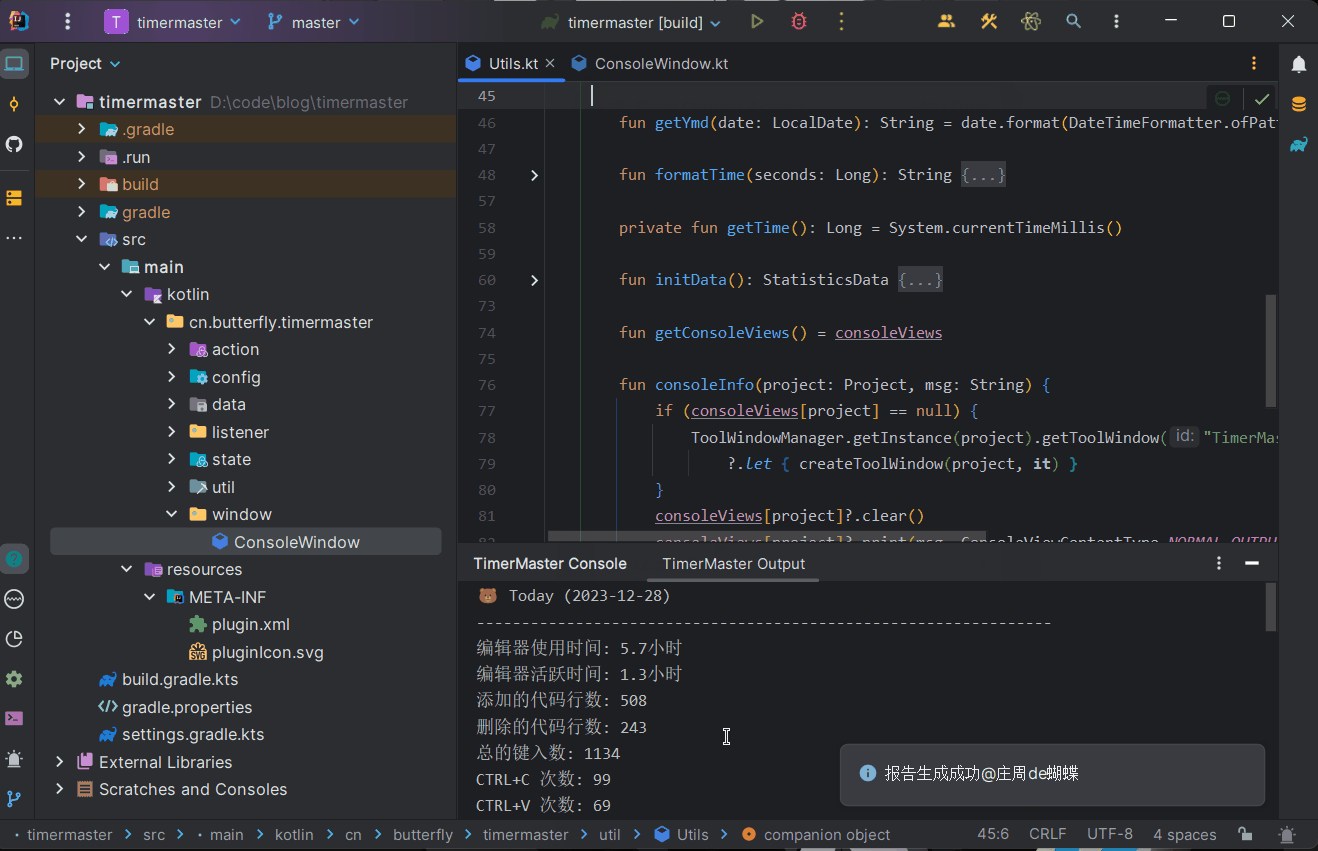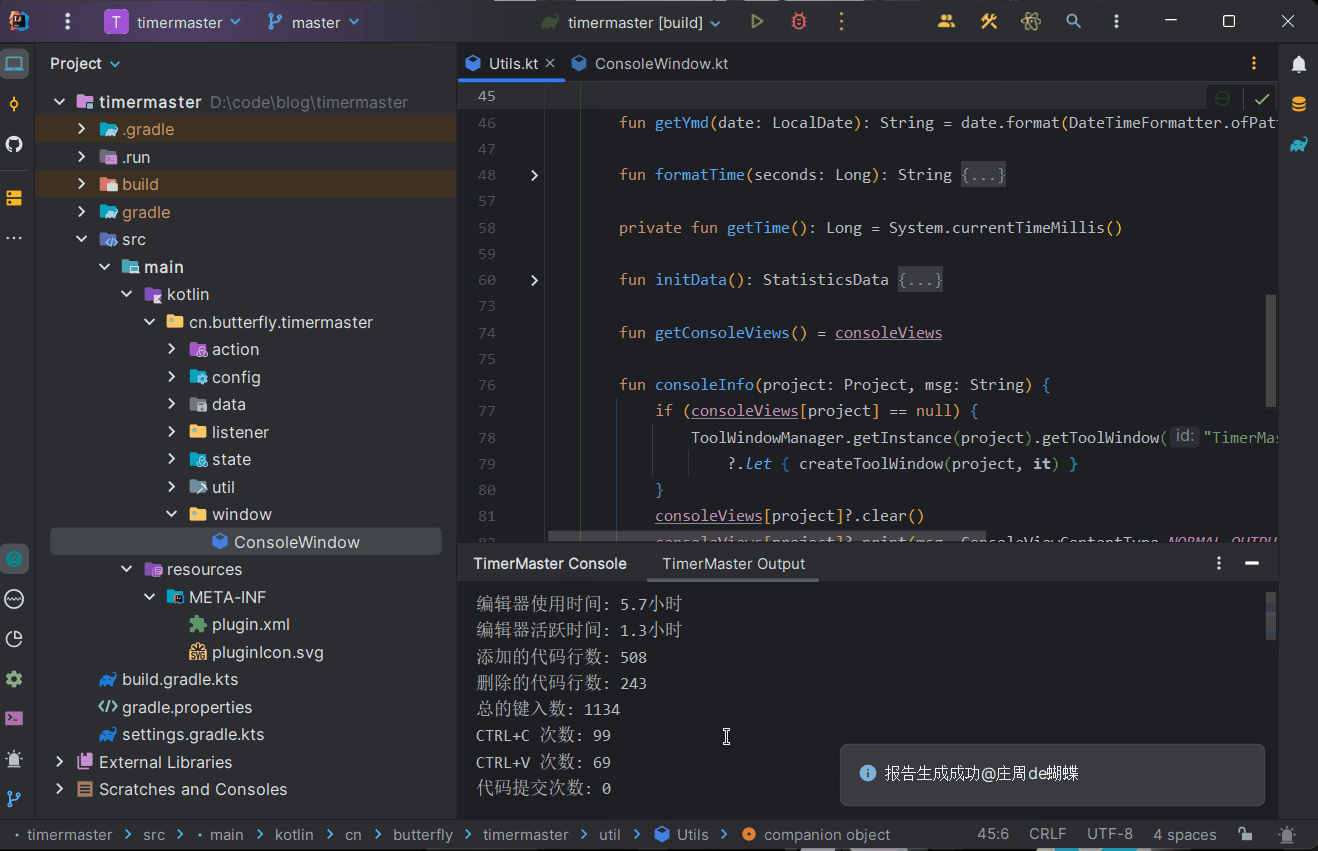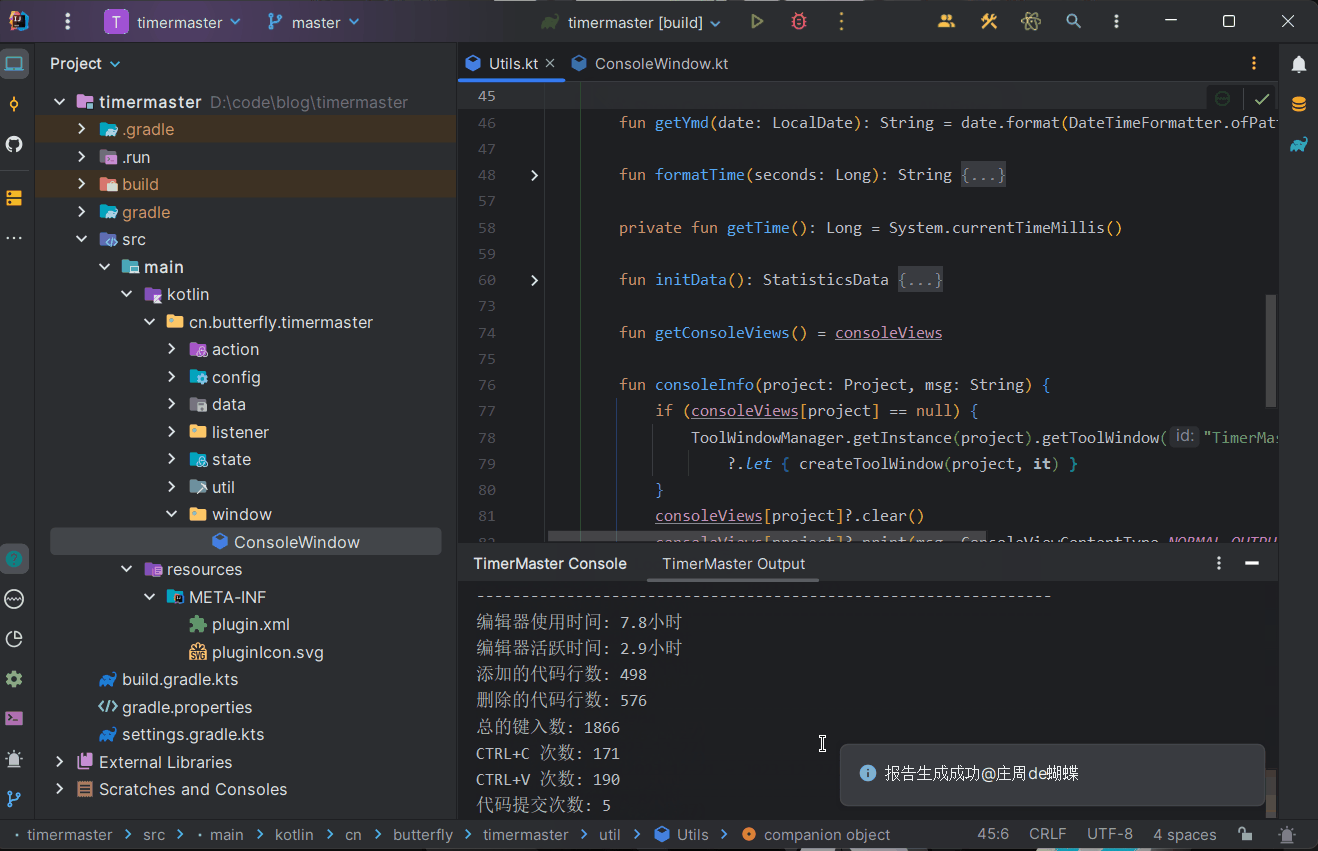
IntelliJ IDE 插件开发 | (四)开发一个时间管理大师插件
系列文章 IntelliJ IDE 插件开发 |(一)快速入门IntelliJ IDE 插件开发 |(二)UI 界面与数据持久化IntelliJ IDE 插件开发 |(三)消息通知与事件监听IntelliJ IDE 插件开发 |(四)开发一…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...
