LeetCode第63题 - 不同路径 II
题目
解答
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;if (obstacleGrid[0][0] == 1) {return 0;}if (obstacleGrid[m - 1][n - 1] == 1) {return 0;}int[][] dp = new int[m][n];dp[0][0] = 1;for (int i = 1, imax = m; i < imax; ++i) {if (obstacleGrid[i][0] == 1) {dp[i][0] = 0;} else {dp[i][0] = dp[i - 1][0];}}for (int j = 1, jmax = n; j < jmax; ++j) {if (obstacleGrid[0][j] == 1) {dp[0][j] = 0;} else {dp[0][j] = dp[0][j - 1];}}for (int i = 1, imax = m; i < imax; ++i) {for (int j = 1, jmax = n; j < jmax; ++j) {if (obstacleGrid[i][j] == 1) {dp[i][j] = 0;} else {if (obstacleGrid[i - 1][j] == 0) {dp[i][j] += dp[i - 1][j];}if (obstacleGrid[i][j - 1] == 0) {dp[i][j] += dp[i][j - 1];}}}}return dp[m - 1][n - 1];}
}
要点
本题目充分说明,使用动态规划解题时,初始值很重要。
另外,假如起点和终点均为障碍物的话,可以直接返回,不需要执行后续的求解操作。
准备的用例,如下
@Before
public void before() {t = new Solution();
}@Test
public void test001() {assertEquals(2, t.uniquePathsWithObstacles(new int[][] { { 0, 0, 0 }, { 0, 1, 0 }, { 0, 0, 0 } }));
}@Test
public void test002() {assertEquals(1, t.uniquePathsWithObstacles(new int[][] { { 0, 1 }, { 0, 0 } }));
}@Test
public void test003() {assertEquals(1, t.uniquePathsWithObstacles(new int[][] { { 0, 0 } }));
}@Test
public void test004() {assertEquals(0, t.uniquePathsWithObstacles(new int[][] { { 0, 0 }, { 1, 1 }, { 0, 0 } }));
}@Test
public void test005() {assertEquals(0, t.uniquePathsWithObstacles(new int[][] { { 0, 0 }, { 0, 1 } }));
}@Test
public void test006() {assertEquals(0, t.uniquePathsWithObstacles(new int[][] { { 1, 0 }, { 0, 0 } }));
}@Test
public void test007() {assertEquals(0, t.uniquePathsWithObstacles(new int[][] { { 0, 1, 0, 0, 0 }, { 1, 0, 0, 0, 0 }, { 0, 0, 0, 0, 0 }, { 0, 0, 0, 0, 0 } }));
}
相关文章:

LeetCode第63题 - 不同路径 II
题目 解答 class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m obstacleGrid.length;int n obstacleGrid[0].length;if (obstacleGrid[0][0] 1) {return 0;}if (obstacleGrid[m - 1][n - 1] 1) {return 0;}int[][] dp new int[m][n];dp…...
python+django网上银行业务综合管理系统vue_bvj8b
本课题主要研究如何用信息化技术改善传统网上银行综合管理行业的经营和管理模式,简化网上银行综合管理的难度,根据管理实际业务需求,调研、分析和编写系统需求文档,设计编写符合银行需要的系统说明书,绘制数据库结构模…...

【软件工程】走进瀑布模型:传统软件开发的经典之路
🍎个人博客:个人主页 🏆个人专栏: 软件工程 ⛳️ 功不唐捐,玉汝于成 目录 前言: 正文 主要阶段: 优点: 缺点: 应用范围: 结语 我的其他博客 前言&am…...
C卷 (JavaPythonNode.jsC语言C++))
两个字符串间的最短路径问题 (100%用例)C卷 (JavaPythonNode.jsC语言C++)
给定两个字符串,分别为字符串A与字符串B。例如A字符串为ABCABBA,B字符串为CBABAC可以得到下图m*n的二维数组,定义原点为(0,0),终点为(m,n),水平与垂直的每一条边距离为1,映射成坐标系如下图 从原点(0,0)到(0,A)为水平边,距离为1,从(0,A)到(A,C)为垂直边,距离为1;假设两…...

通过ADB来实现脚本来控制手机
ADB 简介 adb的全称为Android Debug Bridge,安卓调试桥,可以通过调试命令来控制手机,诸如开机,关机等按键控制;或者启动,关闭应用;异或进行触摸模拟. 通过学习adb,可以实现简单的脚本控制,最大的特点是不需要root,对于普通手机都可以进行,帮助我们完成一些简单的重复性事件,…...
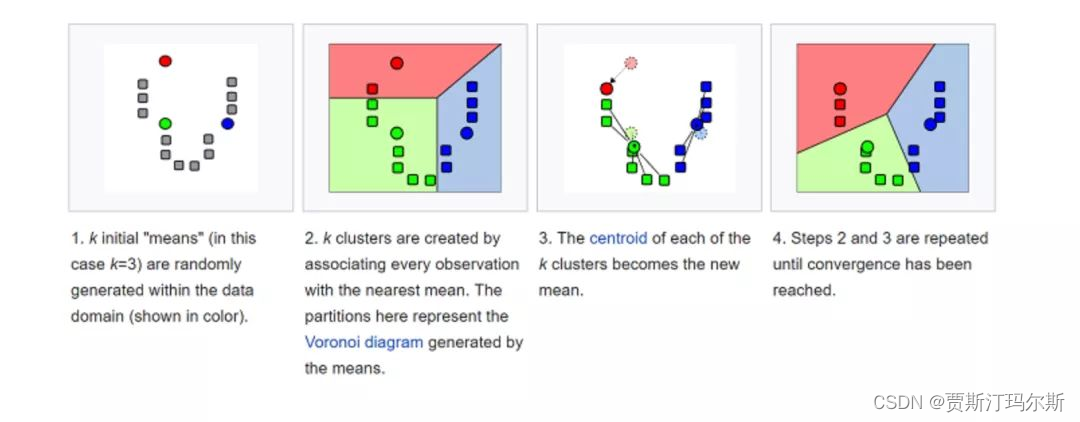
机器学习之K-means聚类
概念 K-means是一种常用的机器学习算法,用于聚类分析。聚类是一种无监督学习方法,它试图将数据集中的样本划分为具有相似特征的组(簇)。K-means算法的目标是将数据集划分为K个簇,其中每个样本属于与其最近的簇中心。 以下是K-means算法的基本步骤: 选择簇的数量(K值)…...

SSH 端口转发:如何将服务绑定到本地 IP 地址
在日常工作中,我们经常需要访问位于远程服务器上的服务,如数据库、Web 应用程序或其他类型的服务器。直接访问这些服务可能会因为安全限制或网络配置而变得复杂或不可能。这时,SSH 端口转发就成了我们的得力助手。在本篇博客中,我…...
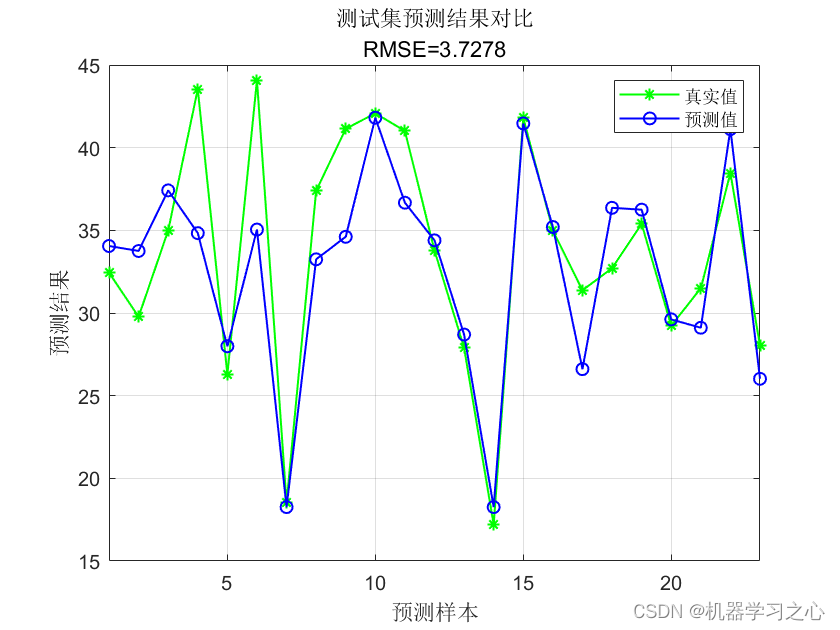
回归预测 | MATLAB实ZOA-LSTM基于斑马优化算法优化长短期记忆神经网络的多输入单输出数据回归预测模型 (多指标,多图)
回归预测 | MATLAB实ZOA-LSTM基于斑马优化算法优化长短期记忆神经网络的多输入单输出数据回归预测模型 (多指标,多图) 目录 回归预测 | MATLAB实ZOA-LSTM基于斑马优化算法优化长短期记忆神经网络的多输入单输出数据回归预测模型 (…...
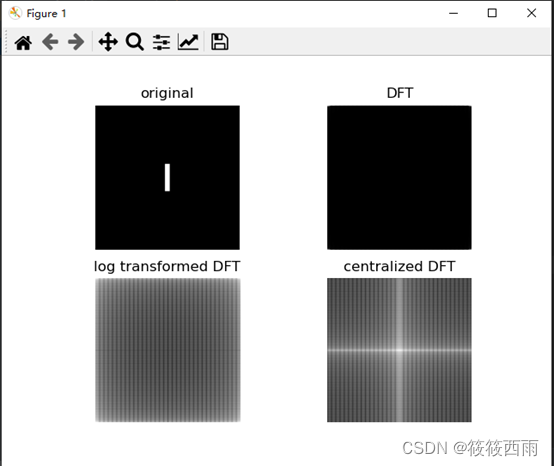
python实现图像的二维傅里叶变换——冈萨雷斯数字图像处理
原理 二维傅里叶变换是一种在图像处理中常用的数学工具,它将图像从空间域(我们通常看到的像素排列)转换到频率域。这种变换揭示了图像的频率成分,有助于进行各种图像分析和处理,如滤波、图像增强、边缘检测等。 在数学…...

We are a team - 华为OD统一考试
OD统一考试 题解: Java / Python / C 题目描述 总共有 n 个人在机房,每个人有一个标号 (1<标号<n) ,他们分成了多个团队,需要你根据收到的 m 条消息判定指定的两个人是否在一个团队中,具体的: 消息构成为 a b …...

NFC物联网智慧校园解决方案
近场通信(Near Field Communication,NFC)又称近距离无线通信,是一种短距离的高频无线通信技术,允许电子设备之间进行非接触式点对点数据传输交换数据。这个技术由免接触式射频识别(RFID)发展而来,并兼容 RFID,主要用于…...

鸿蒙系列--组件介绍之容器组件
一、Badge 描述:给其他组件添加标记 子组件:支持单个子组件 1.创建数字标记 Badge(value: {count: number, position?: BadgePosition, maxCount?: number, style: BadgeStyle}) 2.创建字符串标记 Badge(value: {value: string, position?: Badge…...

perl使用find函数踩坑
前言 写了一个脚本可以同时检查多个仿真log文件,并生成html表格。按照文件修改时间从新到旧排序。但是一直无法使用stat函数获取修改时间。 结论:find函数会改变程序执行的当前目录,find(\&process_files, $dir);函数是在$dir目录下运行…...
Java IDEA JUnit 单元测试
JUnit是一个开源的 Java 单元测试框架,它使得组织和运行测试代码变得非常简单,利用JUnit可以轻松地编写和执行单元测试,并且可以清楚地看到哪些测试成功,哪些失败 JUnit 还提供了生成测试报告的功能,报告不仅包含测试…...

深入理解 c++ 函数模板
函数模板是C中的一种强大特性,它允许程序员编写一个可以处理多种数据类型的函数。通过使用模板,我们可以编写一次函数,然后在多种数据类型上使用它,这大大提高了代码的复用性。 1. 基本概念 函数模板是一种参数化类型的工具&…...
系列十二、Linux中安装Zookeeper
一、Linux中安装Zookeeper 1.1、下载安装包 官网:Index of /dist/zookeeper/zookeeper-3.4.11 我分享的链接: 链接:https://pan.baidu.com/s/14Hugqxcgp89f2hqGWDwoBw?pwdyyds 提取码:yyds 1.2、上传至/opt目录 1.3、解…...
k8s之陈述式资源管理
1.kubectl命令 kubectl version 查看k8s的版本 kubectl api-resources 查看所有api的资源对象的名称 kubectl cluster-info 查看k8s的集群信息 kubectl get cs 查看master节点的状态 kubectl get pod 查看默认命名空间内的pod的信息 kubectl get ns 查看当前集群所有的命…...

7天玩转 Golang 标准库之 http/net
在构建web应用时,我们经常需要处理HTTP请求、做网页抓取或者搭建web服务器等任务,而Go语言在这方面为我们提供了强大的内置工具:net/http标准库,它为我们操作和处理HTTP协议提供了便利。 基础用法 一:处理HTTP请求 首…...

钡铼技术集IO数据采集可编程逻辑控制PLC无线4G环保物联网关
背景 数据采集传输对于环保企业进行分析和决策是十分重要的,而实时数据采集更能提升环保生产的执行力度,从而采取到更加及时高效的措施。因此实时数据采集RTU成为环保企业的必备产品之一。 产品介绍 在推进环保行业物联网升级过程中,环保RTU在…...
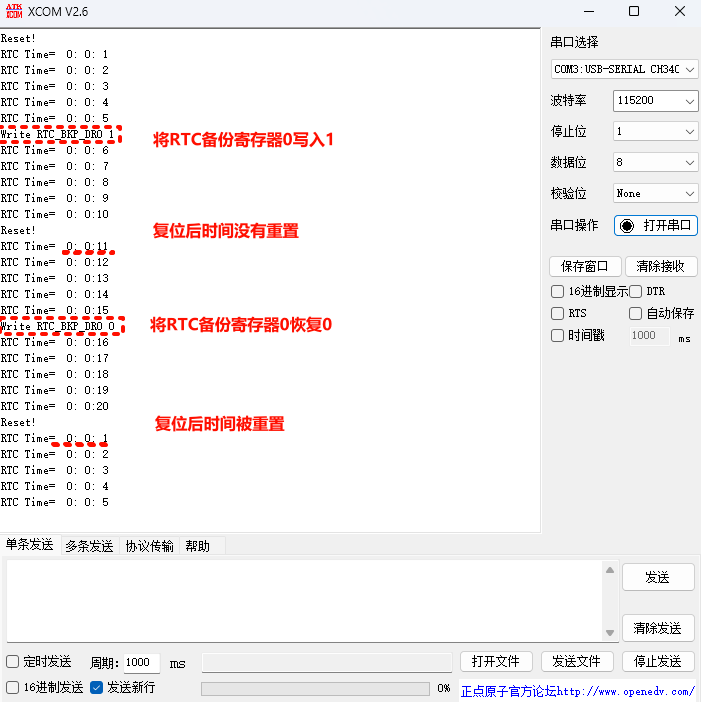
STM32CubeMX教程10 RTC 实时时钟 - 周期唤醒、闹钟A/B事件和备份寄存器
目录 1、准备材料 2、实验目标 3、实验流程 3.0、前提知识 3.1、CubeMX相关配置 3.1.1 、时钟树配置 3.1.2、外设参数配置 3.1.3 、外设中断配置 3.2、生成代码 3.2.1、外设初始化函数调用流程 3.2.2、外设中断函数调用流程 3.2.3、添加其他必要代码 4、常用函数 …...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
