基于图搜索的自动驾驶规划算法 - BFS,Dijstra,A*
本文将讲解BFS,Dijstra,A*,动态规划的算法原理,不正之处望读者指正,希望有兴趣的读者能在评论区提出一些这些算法的面试考点,共同学习,一起进步
0 图论基础
图有三种:无向图、有向图、带权重的图
无向图

有向图

带权重的图

1 BFS
广度优先搜索算法
利用队列queue数据结构实现:先进先出
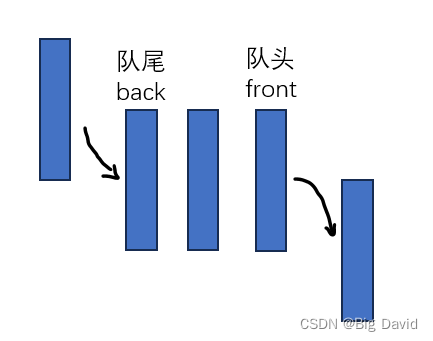
算法流程(伪代码):
BFS(G, start, goal):let Q be queue;Q.push(start);mark start as visited;while (!Q.empty()){v = Q.front();Q.pop();if (v is the goal) return v;for all neighbours n of v in GQ.push(n);n->parent = v;mark n as visited;}
BFS总结:
(1)相同探索所有的方向
(2)如果所有边权重为1,那么用BFS搜索出来的路径是cost最优的
(3)在不同的场景中,不能保证所有的边权重为1,对于这些场景,BFS受限
2 Dijstra
核心思想:
(1)相比BFS,Dijstra维护一个新变量g(n),g(n)表示从起始节点到当前节点的累积成本
(2)从openset(Min-priority queue)中访问累积成本g最低的节点
算法流程(伪代码):
Dijstra(G, start, goal):let open_list be priority_queue;open_list.push(start, 0);g[start] = 0;while (!open_list.empty()){current = open_list.pop();mark current as visited;if (current is the goal) return current;for (all unvisited neightbours next of current in G){next_cost = g[current] + cost(current, next);if (next is not in open_list)open_list.push(next, next_cost);else {if (g[next] > next_cost)g[next] = next_cost;}}}
优点:
(1)Dijstra算法能找到从起始节点到图上所有其他节点的最短路径
(2)Dijstra算法满足最优性
缺点:每次都会从open_list寻找代价最少的节点,但是并不知道终点在哪,如果用这个算法做图中特定两个点的最短路径,是比较低效的
3 A*算法
A*算法手撕版本见手撕A算法(详解A算法)
核心思想:
(1)相比Dijstra,A*将目标点的成本估计为启发式信息以提高效率
(2)启发式函数h(n):表示从节点n到目标的估计成本
(3)评估每个节点的成本函数:f(n)=g(n)+h(n)
(4)从open_list选择f-score最低的节点,而不是Dijstra算法中的g-score
算法流程(伪代码):
Astar(G, start, goal):let open_list be priority_queue;g[start] = 0;f[start] = g[start] + h[start];open_list.push(start, f[start]);while (!open_list.empty()){current = open_list.pop();mark current as visited;if (current is the goal) return current;for all unvisited neighbours next of current in Gnext_cost = g[current] + cost(current, next);if (next is not in open_list)open_list.push(next, next_cost + h[next]);else{if (g[next] > next_cost) {g[next] = next_cost;f[next] = next_cost + h[next];}}}
启发式函数设计
在路径搜索过程中,没有唯一启发函数设计原则,需要根据特定的任务来设计,如果最优性和距离相关,则可以计算节点之间的直线距离来估计
三种常用的距离:
起点: ( p 1 , p 2 ) (p_1, p_2) (p1,p2) 终点: ( q 1 , q 2 ) (q_1, q_2) (q1,q2)
(1)Euclidian distance
d ( p , q ) = ( q 1 − p 1 ) 2 + ( q 2 − p 2 ) 2 d(p,q)=\sqrt{(q_1-p_1)^2+(q_2-p_2)^2} d(p,q)=(q1−p1)2+(q2−p2)2
(2)Manhattan distance
d ( p , q ) = ∣ q 1 − p 1 ∣ + ∣ q 2 − p 2 ∣ d(p,q)=|q_1 - p_1|+|q_2 - p_2| d(p,q)=∣q1−p1∣+∣q2−p2∣
(3)Great circle distance

△ σ = a r c c o s ( s i n ϕ 1 s i n ϕ 2 + c o s ϕ 1 c o s ϕ 2 c o s ( △ λ ) ) \bigtriangleup \sigma =arccos(sin\phi _1sin\phi_2+cos\phi_1cos\phi_2cos(\bigtriangleup\lambda )) △σ=arccos(sinϕ1sinϕ2+cosϕ1cosϕ2cos(△λ))
d = r △ σ d = r\bigtriangleup \sigma d=r△σ
最优性
启发式函数 h ( n ) < c o s t ( n , g o a l ) h(n)<cost(n,goal) h(n)<cost(n,goal)
只要启发式函数提供了小于实际成本的估计,A*将始终找到最优路径,并且通常比Dijstra快
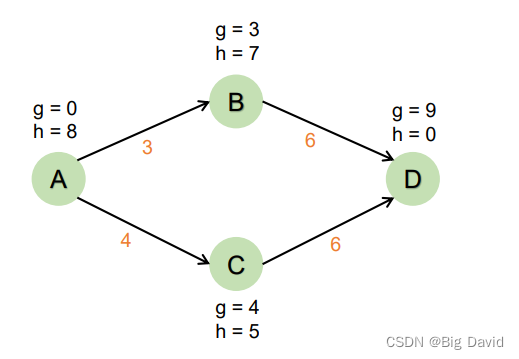
实际上A->B->D是最短路径
因为B的启发式函数高估了对目标的成本
这种高估导致搜索算法相信节点C总成本低于节点B,使得节点C在节点B之前访问,导致结果不是最优路径
在gridmap中如何设计启发式函数

使用8连接,曼哈顿距离启发式高估了成本
欧几里得距离总是可以接受
A*算法的精度和效率

(1) h ( n ) = 0 h(n)=0 h(n)=0:A退化为Dijstra
(2) h ( n ) < c o s t ( n , g o a l ) h(n)<cost(n,goal) h(n)<cost(n,goal):A满足最优性,效率比Dijstra更高
(3) h ( n ) = c o s t ( n , g o a l ) h(n)=cost(n,goal) h(n)=cost(n,goal):A满足最优性,并且有最高的效率
(4) h ( n ) > c o s t ( n , g o a l ) h(n)>cost(n,goal) h(n)>cost(n,goal):A不满足最优性,高估实际成本
BFS、Dijstra、A*总结:
| BFS | Dijstra | A* |
|---|---|---|
| (1)BFS算法会朝着周围等价扩展 | (1)相比BFS,Dijstra倾向于累积成本最小化,不是平等地搜索所有可能的路径,能在加权图中满足最优性 | (1)A*是Dijstra的修改,添加了启发式函数h(n)提高搜索效率 |
| (2)如果每条边权重为1,BFS搜索出来的path也是最优解 | (2)如果每条边权重为1,BFS=Dijstra | (3)启发式函数的设计会影响效率和准确性 |
搜索算法可视化参考:http://qiao.github.io/PathFinding.js/visual/
4 动态规划
- 定义:
一种计算机编程方式,首先把算法问题分解为子问题,求解这些子问题,并把这些结果保存下来,然后优化子问题找到整个问题的最优解
- 动态规划的性质:
(1)最优子结构
面对一个大问题可以分解为一系列子问题。如果能找到每个小问题的最优解,并且能够把小问题拼成大的问题。这种问题就叫最优子结构
(2)重复的子问题
动态规划不会重新计算重复的子问题,会事先保存结果
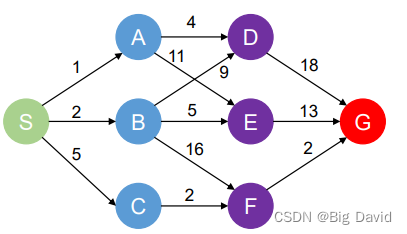
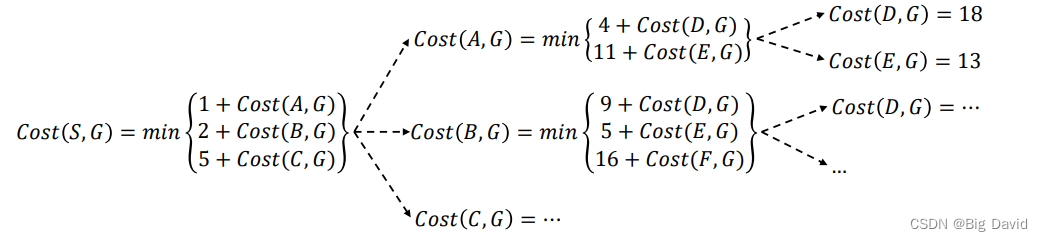
3. 计算方法
(1)前向法
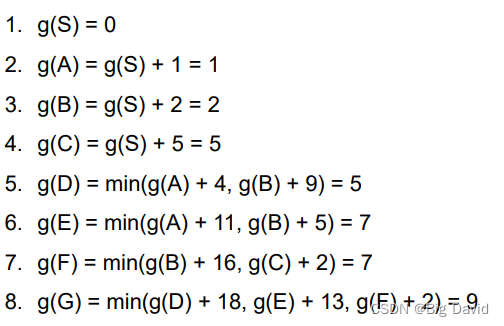
(2)逆向法
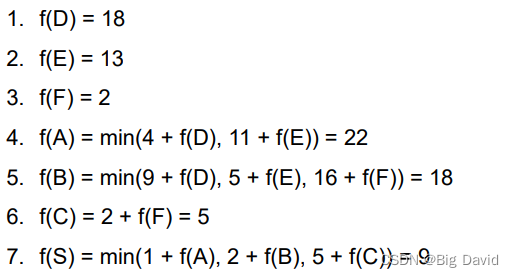
相关文章:
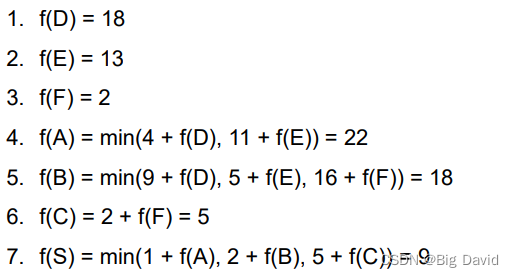
基于图搜索的自动驾驶规划算法 - BFS,Dijstra,A*
本文将讲解BFS,Dijstra,A*,动态规划的算法原理,不正之处望读者指正,希望有兴趣的读者能在评论区提出一些这些算法的面试考点,共同学习,一起进步 0 图论基础 图有三种:无向图、有向…...
Spring系列学习四、Spring数据访问
Spring数据访问 一、Spring中的JDBC模板介绍1、新建SpringBoot应用2、引入依赖:3、配置数据库连接,注入dbcTemplate对象,执行查询:4,测试验证: 二、整合MyBatis Plus1,在你的项目中添加MyBatis …...
)
HBase 创建不分裂的表 ( 禁止 Table Split )
注意:由于 HBase 版本众多,配置表的语法在不同版本上会有差异,本文介绍的配置方法是在 1.4.9 版本上测试的,使用 HBase 2.0 的版本需要核实并修改相关配置方法! 有时候,出于特殊需要,我们希望对…...

docker入门概念详解
本篇文章对docker的一些基础概念和周边概念进行了详细解释。帮助你可以很好的理解docker是用来干什么的,docker是怎么工作的。其中有docker所运用到的技术解释,docker的不同发展版本,dokcer的架构,docker的生态等等详解。希望本片…...

C++程序设计实践报告【格式】
C程序设计实践报告 原XX工业学院 C程序设计实践报告 题目: 专业: 学号: 姓名: 年 月 日 目录 一、绪…...

浅谈数据仓库运营
一、背景 企业每天都会产生大量的数据,随着时间增长,数据会呈现几何增长,尤其在系统基建基础好的公司。好的数据仓库需要提前规划和好的运营,才能支持企业的发展,为企业提供数据分析基础。 二、目标 提高数据仓库存储…...
系列六、Consul
一、Consul 1.1、概述 Consul是一套开源的分布式服务发现和配置管理系统,由HashiCorp公司用Go语言开发。他提供了微服务系统中的服务治理、配置中心、控制总线等功能。这些功能中的每一个功能都可以单独使用,也可以一起使用以构建全方位的服务网格&…...

Java集合/泛型篇----第一篇
系列文章目录 文章目录 系列文章目录前言一、ArrayList和linkedList的区别二、HashMap和HashTable的区别三、Collection包结构,与Collections的区别四、泛型常用特点前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站…...

集合使用注意事项
集合使用注意事项总结 集合判空 判断所有集合内部的元素是否为空,使用 isEmpty() 方法,而不是 size()0 的方式 这是因为 isEmpty() 方法的可读性更好,并且时间复杂度为 O(1)。 集合转 Map 在使用 java.util.stream.Collectors 类的 toMap()…...

什么是 JavaScript 中的 WeakMap
在 JavaScript 中,WeakMap 是一种特殊的 Map 数据结构,它允许将对象作为键,而且键值对是弱引用的关系。 与 Map 不同的是,WeakMap 的键只能是对象,不能是其他类型的值。同时,当键对象没有任何引用时&#…...
nodejs+vue+ElementUi农产品团购销售系统zto2c
目标是为了完成小区团购平台的设计和实现,在疫情当下的环境,方便小区业主购入生活所需,减小居民的生活压力 采用B/S模式架构系统,开发简单,只需要连接网络即可登录本系统,不需要安装任何客户端。开发工具采…...
nacos入门篇001-安装与启动
1、下载zip包 我这里下载的是版本2.2.0 Nacos 快速开始 2、修改配置文件 2.1集群模式修改成单例模式 vi startup.sh 2.2 修改数据库配置信息 3、初始化数据库 3.1 创建db名称:db_nacos 3.2 执行mysql-schema.sql 3.3 执行完截图: 4、运行脚本启动 …...
WordPress主题大前端DUX v8.3源码下载
DUX主题8.3版本更新内容: 新增:Cloudflare Turnstile 免费验证功能 新增:子菜单页面模版,支持多级页面 新增:手机端文章内表格自动出现横向滚动条,可集体或单独设置滚动宽度 新增:标签云页面模版…...
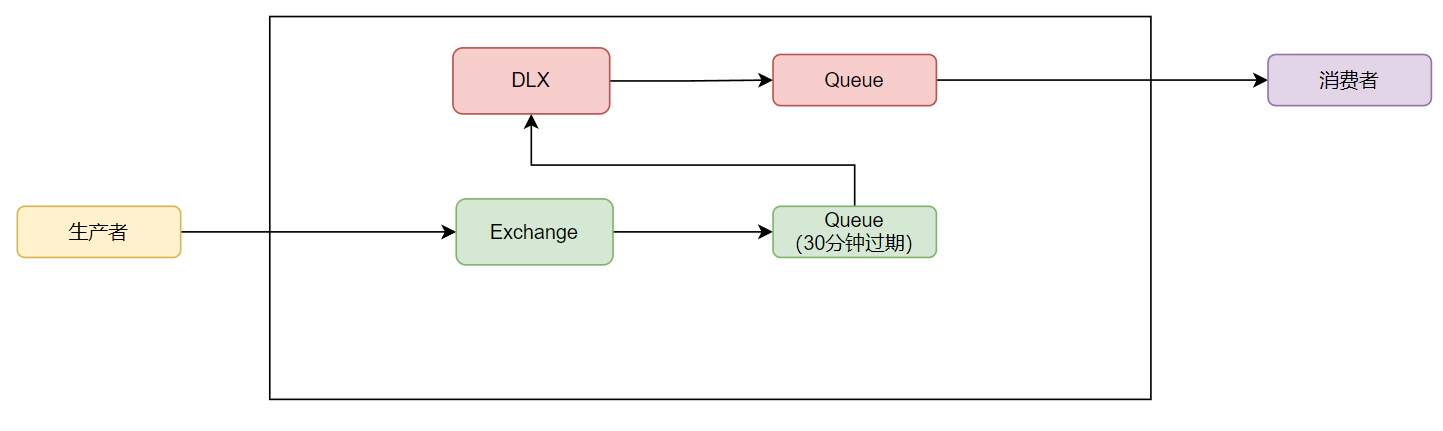
RabbitMQ之快速入门、上手
前言 学习一样新技术、新框架,最重要的是学习其思想、原理。即原理性思维。 如果是因为工作原因,需要快速上手RabbitMQ,本篇或许适合你。 核心概念 Connection:publisher/consumer 和 broker 之间的 TCP 连接Channel…...
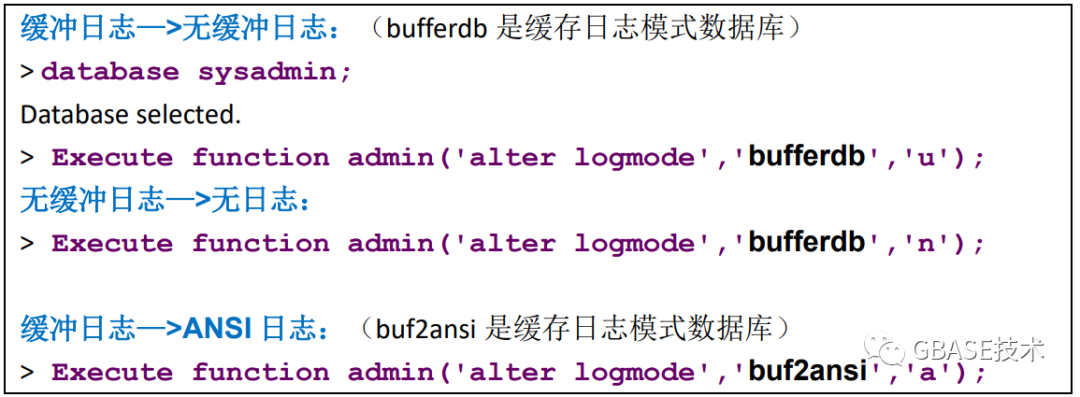
GBASE南大通用-GBase 8s数据库日志模式及切换
一、 GBase 8s数据库共有以下 4 种日志模式:无日志模式、缓冲日志模式、无缓冲日志模式、ANSI 模式。详细介绍如下: 1、无日志模式(Non logging): 采用无日志模式时,所有 DML 操作都不会被记录到日志中&…...

侵入式和非侵入式微服务框架的比较
微服务框架可以分为侵入式和非侵入式两种。侵入式框架需要对现有代码进行改造,而非侵入式框架则无需改造现有代码。 侵入式框架 侵入式框架将微服务治理功能嵌入到应用程序中,需要修改应用程序的代码。这种框架的优点是可以提供更强大的功能࿰…...

Go语言程序设计-第5章--函数
Go语言程序设计-第5章–函数 5.1 函数声明 每个函数声明都包含一个名字、一个形参列表、一个可选的返回列表以及函数体: func name(parameter-list) (result-list) {body }func add(x int, y int) int { return x y} func sub(x, y int) (z int) {z x - y; return} func f…...

数据被锁?被.mkp 勒索病毒攻击后的拯救行动
导言: 网络安全面临着越来越多的挑战,而.mallox勒索病毒则成为数字威胁中的一股强大势力。它的威胁不仅体现在其高度复杂的加密算法上,还表现在对受感染系统的深度渗透和数据的极大破坏上。以下是.mallox勒索病毒的主要威胁:如不…...

Fine-Tuning Language Models from Human Preferences
Abstract 奖励学习(reward learning)可以将强化学习(RL)应用到由人类判断定义奖励的任务中,通过询问人类问题来构建奖励模型。奖励学习的大部分工作使用了模拟环境,但是关于价值的复杂信息经常是以自然语言的形式表达的。我们相信语言奖励学习是使强化学习在现实世界任务…...
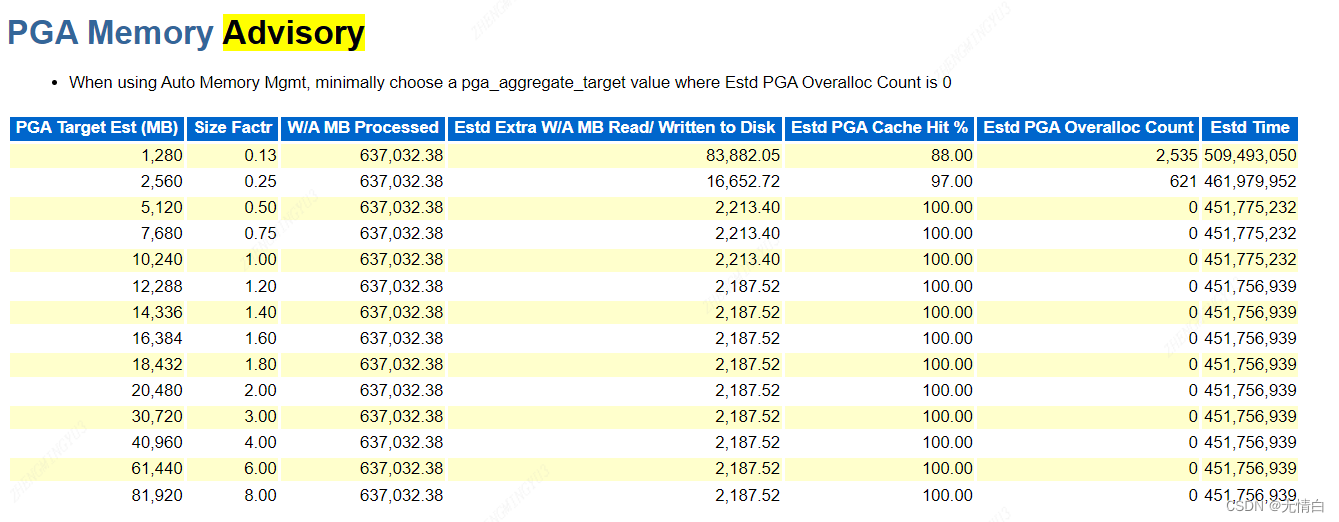
提升数据库性能的关键指南-Oracle AWR报告
文章目录 一、了解AWR报告:数据库性能的仪表盘二、生成AWR报告三、解读AWR报告的关键部分1.报告开头的系统基础信息2.ADDM发现3.负载概览(Load Profile)4.参数文件5.顶级前台等待事件6.SQL 统计信息-顶级SQL7.SGA Advisory AND PAG Advisory 一、了解AWR报告&#x…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
