力扣:62. 不同路径(动态规划,附python二维数组的定义)
题目:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右
- 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109
思路:
刚看到这道题第一时间想不到这跟动态规划有什么关系,这不是图的深搜吗?
但大家试过之后就会发图的深搜会超时。
动态规划:
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
按照动规五部曲来分析:
- 确定dp数组,以及下标的含义
这里要明确dp数组的含义,定义dp数组是为了找到不同路径,
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
这道题的递归公式不像之前的题一下就能看出来,
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
可能有人会疑惑 dp[i - 1][j] 向下走一步就到dp[i][j],dp[i][j - 1]向右走一步就到dp[i][j],那为什么dp[i][j] 不等于 dp[i - 1][j] + dp[i][j - 1] + 1 + 1 呢?这里要明白dp数组的含义,这里dp数组求的是路径而不是步数,你走一步路径数并没有发生变化。
- dp数组的初始化
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
- 确定遍历顺序
这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
- 举例推导dp数组
如图所示:
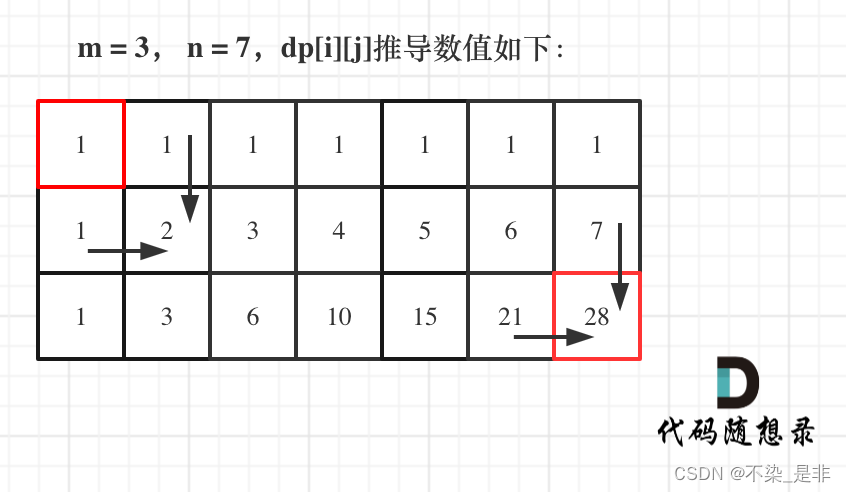
这里要说明一下dp数组的日志打印,如果你提交不通过,你可以直接输出dp数组,看看你是哪一步出现问题,然后对症下药。
定义二维数组
写过很多要定义二维数组的题了,但依然是一写就忘,这里稍微说一下python中二维数组的定义,
方法一:
dp = [[0] * n for _ in range(m)]
方法二(跟一其实是一个东西):
dp = [[0 for i in range(n)] for j in range(m)]
方法三(NumPy库):
import numpy as np# 创建一个n×m的二维数组,初始值为0 np.ones((n, m)) 初始值为1
array = np.zeros((n, m))
完整代码:
class Solution:def uniquePaths(self, m: int, n: int) -> int:# 创建一个二维列表用于存储唯一路径数dp = [[0] * n for _ in range(m)]# 设置第一行和第一列的基本情况for i in range(m):dp[i][0] = 1for j in range(n):dp[0][j] = 1# 计算每个单元格的唯一路径数for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i - 1][j] + dp[i][j - 1]# 返回右下角单元格的唯一路径数return dp[m - 1][n - 1]
复杂度分析:
- 时间复杂度:O(m × n)
- 空间复杂度:O(m × n)
PS:
做完本题可以接着做力扣:63. 不同路径 II,完全一样的思路。
详细见:力扣:63. 不同路径 II(动态规划)
相关文章:

力扣:62. 不同路径(动态规划,附python二维数组的定义)
题目: 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路径&…...
2022年全球运维大会(GOPS深圳站)-核心PPT资料下载
一、峰会简介 GOPS 主要面向运维行业的中高端技术人员,包括运维、开发、测试、架构师等群体。目的在于帮助IT技术从业者系统学习了解相关知识体系,让创新技术推动社会进步。您将会看到国内外知名企业的相关技术案例,也能与国内顶尖的技术专家…...

8868体育助力意甲罗马俱乐部 迪巴拉有望付出
8868体育助力意甲罗马俱乐部 迪巴拉有望付出 意甲罗马俱乐部是8868体育合作球队之一,本赛季,在意甲第14轮的比赛中,罗马客场2-1战胜萨索洛,积分上升到意甲第4位。 有报道称,迪巴拉在对阵佛罗伦萨的比赛中受伤ÿ…...

java设计模式实战【策略模式+观察者模式+命令模式+组合模式,混合模式在支付系统中的应用】
引言 在代码开发的世界里,理论知识的重要性毋庸置疑,但实战经验往往才是知识的真正试金石。正所谓,“读万卷书不如行万里路”,理论的学习需要通过实践来验证和深化。设计模式作为软件开发中的重要理论,其真正的价值在…...

小程序wx:if 和hidden的区别?
在小程序中,wx:if 和 hidden 是用于条件渲染的两种不同方式。 选择使用哪种方式取决于具体情况。如果条件变化频繁或节点包含复杂的子节点,可以考虑使用 wx:if 进行条件渲染;如果条件变化较少且节点结构简单,可以使用 hidden 控制…...
自动驾驶学习笔记(二十三)——车辆控制模型
#Apollo开发者# 学习课程的传送门如下,当您也准备学习自动驾驶时,可以和我一同前往: 《自动驾驶新人之旅》免费课程—> 传送门 《Apollo开放平台9.0专项技术公开课》免费报名—>传送门 文章目录 前言 运动学模型 动力学模型 总结…...

Linux Shell 015-文本双向覆盖重定向工具tee
Linux Shell 015-文本双向覆盖重定向工具tee 本节关键字:Linux、Bash Shell、文本双向覆盖重定向工具 相关指令:tee、echo、cat tee介绍 tee工具是从标准输入读取并写入到标准输出和文件,即:双向覆盖重定向(屏幕输出…...

【PyQt】(自定义类)QIcon派生,更易用的纯色Icon
嫌Qt自带的icon太丑,自己写了一个,主要用于纯色图标的自由改色。 当然,图标素材得网上找。 Qt原生图标与现代图标对比: 没有对比就没有伤害 Qt图标 网络素材图标 自定义类XJQ_Icon: from PyQt5.QtGui import QIc…...

【mysql】数据处理格式化、转换、判断
数据处理 判断是否超时,时间是否大于当前时间计算分钟数时间格式化处理如果数值类型进行转换字符类型字符拼接case-when代替if-else判断数据空(特殊:含空数据、空字符处理) select /*判断是否超时,时间是否大于当前…...

深入探索Java中的UDP网络通信机制
在网络通信中,UDP(User Datagram Protocol,用户数据报协议)是一种无连接的协议,它在某些情况下比TCP更适合,尤其是在要求速度快、对数据准确性要求相对较低的场景下。本文将介绍如何使用Java进行UDP网络通信…...

List常见方法和遍历操作
List集合的特点 有序: 存和取的元素顺序一致有索引:可以通过索引操作元素可重复:存储的元素可以重复 List集合的特有方法 Collection的方法List都继承了List集合因为有索引,所以有了很多操作索引的方法 ublic static void main…...
【基础篇】一、认识JVM
文章目录 1、虚拟机2、Java虚拟机3、JVM的整体结构4、Java代码的执行流程5、JVM的三大功能6、JVM的分类7、JVM的生命周期 1、虚拟机 虚拟机,Virtual Machine,一台虚拟的计算机,用来执行虚拟计算机指令。分为: 系统虚拟机&#x…...
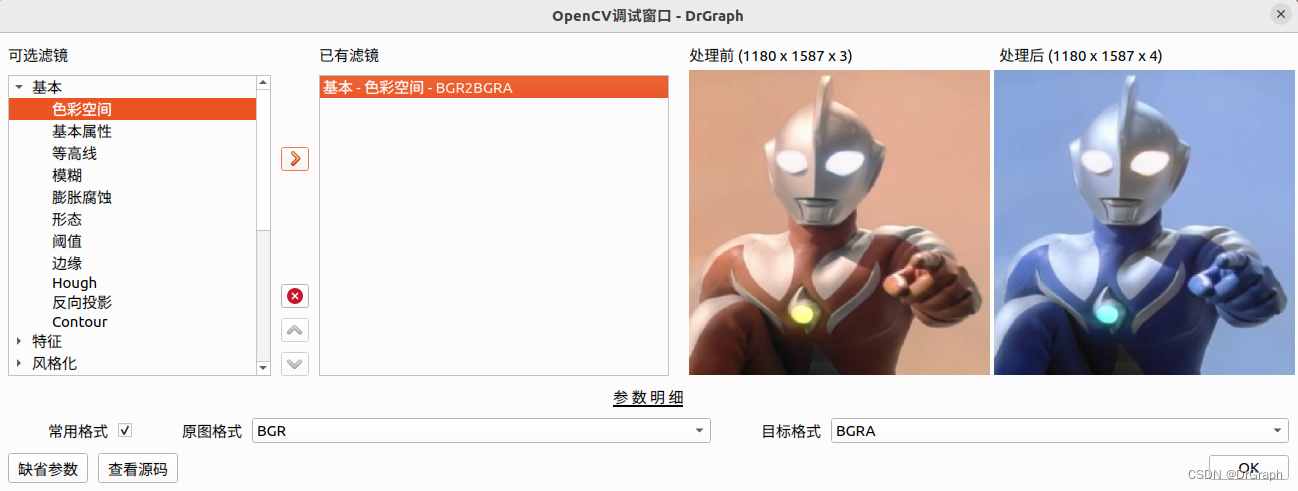
DrGraph原理示教 - OpenCV 4 功能 - 颜色空间
前言 前段时间,甲方提出明确需求,让把软件国产化。稍微研究了一下,那就转QT开发,顺便把以前的功能代码重写一遍。 至于在Ubuntu下折腾QT、OpenCV安装事宜,网上文章很多,照猫画虎即可。 这个过程࿰…...

听GPT 讲Rust源代码--src/tools(36)
File: rust/src/tools/clippy/clippy_lints/src/loops/empty_loop.rs 在Rust源代码中,empty_loop.rs文件位于src/tools/clippy/clippy_lints/src/loops/目录下,它的作用是实现并提供一个名为EMPTY_LOOP的Lint规则。Clippy是一个Rust的静态分析工具&#…...
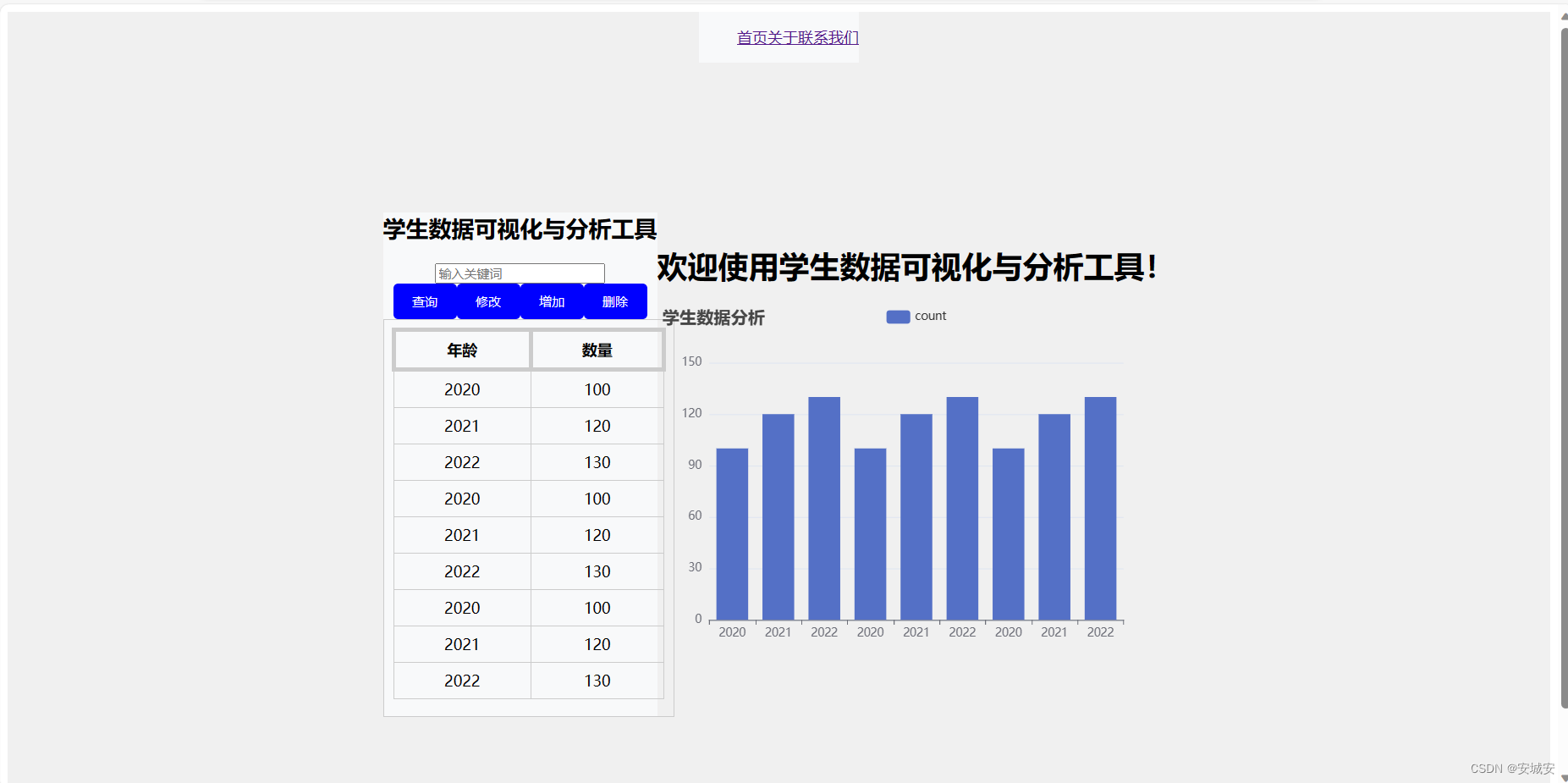
学生数据可视化与分析工具 vue3+flask实现
目录 一、技术栈亮点 二、功能特点 三、应用场景 四、结语 学生数据可视化与分析工具介绍 在当今的教育领域,数据驱动的决策正变得越来越重要。为了满足学校、教师和学生对于数据深度洞察的需求,我们推出了一款基于Vue3和Flask编写的学生数据可视化…...
uni-app condition启动模式配置
锋哥原创的uni-app视频教程: 2023版uniapp从入门到上天视频教程(Java后端无废话版),火爆更新中..._哔哩哔哩_bilibili2023版uniapp从入门到上天视频教程(Java后端无废话版),火爆更新中...共计23条视频,包括:第1讲 uni…...
网大为卸任腾讯CXO;Midjourney 1 月训练视频模型;2023年马斯克赚了7700亿
投融资 • 2023 年大型科技公司在生成式 AI 初创企业上的投资远超风险投资集团• 恒信东方与无锡政府合作成立布局 MR/XR 技术及 3D 数字资产 AIGC 产业投资基金• 新公司法完善注册资本认缴登记制度• 网大为卸任腾讯CXO,曾促成南非MIH的投资• 宁波蔚孚科技完成数…...

据报道,微软的下一代 Surface 笔记本电脑将是其首款真正的“人工智能 PC”
明年,微软计划推出 Surface Laptop 6和 Surface Pro 10,这两款设备将提供 Arm 和 Intel 两种处理器选项。不愿意透露姓名的不透露姓名人士透露,这些新设备将引入先进的人工智能功能,包括配备下一代神经处理单元 (NPU)。据悉&#…...

Springer build pdf乱码
在textstudio中编辑时没有错误,在editor manager生成pdf时报错。 首先不要改源文件,着重看你的上传顺序: 将.tex文件,.bst文件,.cls文件,.bib文件, .bbl文件的类型,在editor manager中是Item。…...
k8s之kudeadm
kubeadm来快速的搭建一个k8s的集群: 二进制搭建适合大集群,50台以上主机 kubeadm更适合中小企业的业务集群 master:192.168.233.91 docker kubelet lubeadm kubectl flannel node1:192.168.233.92 docker kubelet lubeadm kubectl flannel…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
