概率的 50 个具有挑战性的问题 [8/50]:完美的桥牌
一、说明
我最近对与概率有关的问题产生了兴趣。我偶然读到了弗雷德里克·莫斯特勒(Frederick Mosteller)的《概率论中的五十个具有挑战性的问题与解决方案》)一书。我认为创建一个系列来讨论这些可能作为面试问题出现的迷人问题会很有趣。每篇文章只有 1 个问题,使其成为一个总共有 50 个部分的系列。让我们潜入并激活我们的脑细胞🧠!

图片由作者使用 DALL-E 3 提供。
我们经常读到有人在桥牌上被发了 13 个黑桃。
二、问题提出
有了一包洗牌,你得到一手完美牌的几率有多大(一花色中的13张)?
(桥牌是用普通的 52 张牌包玩的,4 种花色各 13 张,4 名玩家每人发 13 张)
三、问题分析
为了计算一手完美牌的概率,我们需要首先检查玩家可以从一副 52 张牌中获得任何 13 张牌的总数。在这种情况下,我们可以使用二项式系数 (52C13) 从 52 张牌中选择 13 张牌,因为我们不关心排序。接下来,让我们专注于一个特定的西装。从特定花色中选择 13 张牌的方法数只是 1,因为每种花色只有 13 张牌。

从 13 张牌和特定花色的 52 张牌和 13 张牌中选择 13 张牌的方法数。
对于完美的手牌,花色的选择无关紧要。因此,我们将发给特定花色的 13 张牌的概率乘以 4,如下所示:

完美手牌的概率
要计算获得完美牌的几率,我们只需要取倒数,结果为 1.588 * 10¹¹。
总之,有了一包洗牌,你得到完美手牌的机会是1600亿分之一。
四、Python 代码
import numpy as npn_simulations = 1000000perfect_hand_count = 0
for _ in range(n_simulations):deck = np.arange(52)np.random.shuffle(deck)player_hand = deck[:13]suits = player_hand // 13if np.all(suits == suits[0]):perfect_hand_count += 1probability = perfect_hand_count / n_simulationsprint(f'Probability of a perfect hand: {probability:.3f}')# Output:
# Probability of a perfect hand: 0.000
# Even after 1 million simulations, the probability of being dealt a perfect hand is still 0.
这就是这个桥牌游戏🃏问题的全部内容。欢迎任何反馈或问题!该代码可在我的 Github 上找到。
相关文章:

概率的 50 个具有挑战性的问题 [8/50]:完美的桥牌
一、说明 我最近对与概率有关的问题产生了兴趣。我偶然读到了弗雷德里克莫斯特勒(Frederick Mosteller)的《概率论中的五十个具有挑战性的问题与解决方案》)一书。我认为创建一个系列来讨论这些可能作为面试问题出现的迷人问题会很有趣。每篇…...
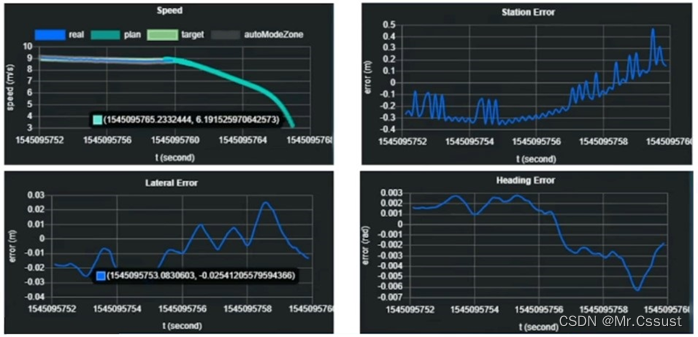
自动驾驶学习笔记(二十四)——车辆控制开发
#Apollo开发者# 学习课程的传送门如下,当您也准备学习自动驾驶时,可以和我一同前往: 《自动驾驶新人之旅》免费课程—> 传送门 《Apollo开放平台9.0专项技术公开课》免费报名—>传送门 文章目录 前言 控制算法 控制标定 控制协议…...

【起草】【第十二章】定制ChatGPT数字亲人
身为普普通通的我们,不知道亲人们在哪一天就要离开这个世界 ? 作为普普通通的程序员,我们可以为我们的亲人做点什么 ? 让他们以数字资产形式留在人世间 ? 对话|6岁女孩病逝捐器官,妈妈:她去…...

MySQL数据库索引
索引的定义 索引是一个排序的列表,包含索引字段的值和其对应的行记录的数据所在的物理地址 索引的作用 加快表的查询速度,还可以对字段排序 索引的副作用 会额外占用磁盘空间;更新包含索引的表会花费更多的时间,效率会更慢 …...

【LLM 】7个基本的NLP模型,为ML应用程序赋能
在上一篇文章中,我们已经解释了什么是NLP及其在现实世界中的应用。在这篇文章中,我们将继续介绍NLP应用程序中使用的一些主要深度学习模型。 BERT 来自变压器的双向编码器表示(BERT)由Jacob Devlin在2018年的论文《BERT:用于语言…...

数字人私人定制
数字人是什么? 在回答这个问题之前,我们先回答另一个问题,人如何与人工智能交流?目前可以通过文字、语音、电脑屏幕、手机屏幕、平板、虚拟现实设备等和人工智能交流,为了得到更好的交流体验,人工智能必然…...

CollectionUtils
使用 CollectionUtils 类的常用方法 在Java开发中,我们经常需要对集合进行各种操作,而Apache Commons Collections库提供了一个方便的工具类 CollectionUtils,其中包含了许多实用的方法。在这篇博客中,我们将深入了解一些常用的方…...

很想写一个框架,比如,spring
很想写一个框架,比如,spring。 原理很清楚,源码也很熟悉。 可惜力不从心,是不是可以找几个小弟一起做。...

Java集合/泛型篇----第五篇
系列文章目录 文章目录 系列文章目录前言一、说说LinkHashSet( HashSet+LinkedHashMap)二、HashMap(数组+链表+红黑树)三、说说ConcurrentHashMap前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通…...
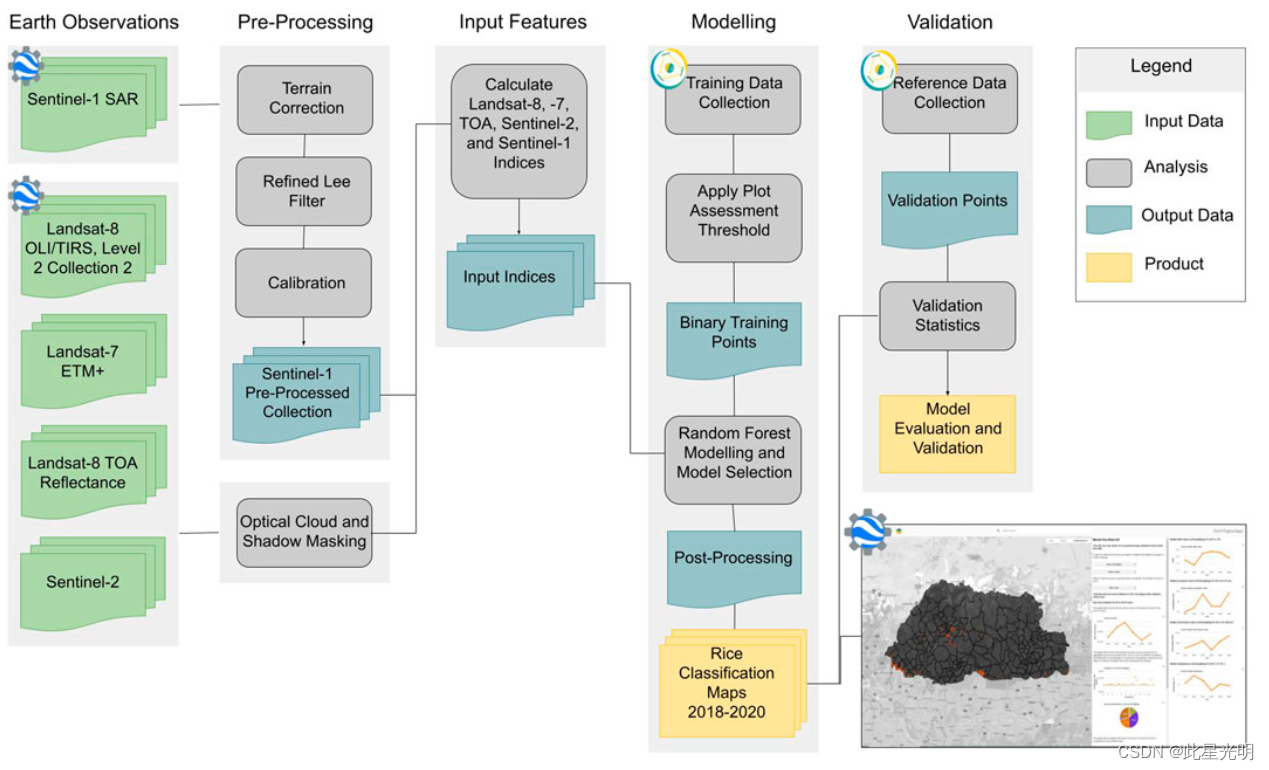
ACES 增强版不丹水稻作物地图(2016-2022 年)
ACES 增强版不丹水稻作物地图(2016-2022 年) 用于改善粮食安全决策的 2016-2022 年年度作物类型稻米地图仍然是不丹的一项挑战。这些地图是与不丹农业部和 SERVIR 合作开发的。通过专注于发展不丹的科学、技术、工程和数学 (STEM),我们共同开…...
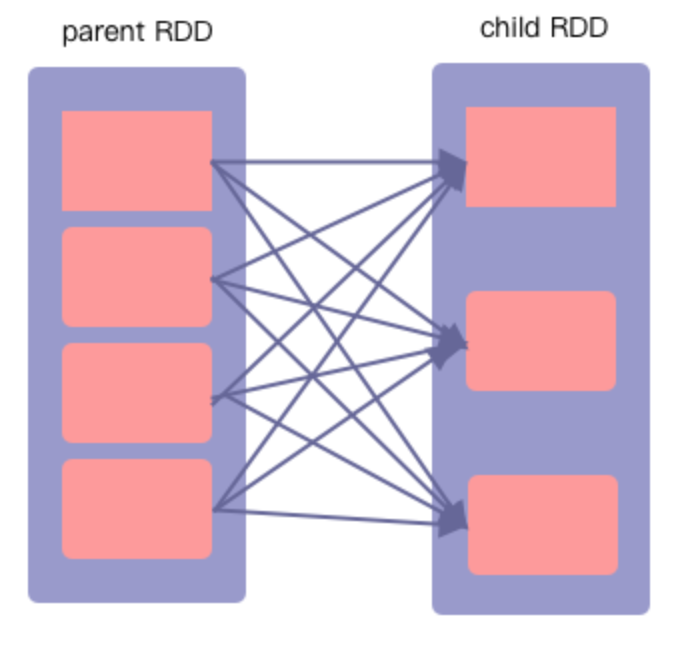
【Spark精讲】一文讲透Spark宽窄依赖的区别
宽依赖窄依赖的区别 窄依赖:RDD 之间分区是一一对应的宽依赖:发生shuffle,多对多的关系 宽依赖是子RDD的一个分区依赖了父RDD的多个分区父RDD的一个分区的数据,分别流入到子RDD的不同分区特例:cartesian算子对应的Car…...

nacos2.3.0配置中心问题处理
问题:Error to process server push response: {"headers":{},"abilityTable":{"supportPersistentInstanceByGrpc":true},"module":"internal"} 处理办法: 将pom.xml中 <!-- nacos服务注册/发…...

Apollo自动驾驶系统:实现城市可持续交通的迈向
前言 「作者主页」:雪碧有白泡泡 「个人网站」:雪碧的个人网站 ChatGPT体验地址 文章目录 前言引言:1. 什么是微服务架构?2. 微服务架构的组成要素3. 微服务架构的挑战和解决方案4. 微服务架构的可扩展性和弹性 第二部分&#x…...

【WPF.NET开发】附加事件
本文内容 先决条件附加事件语法WPF 如何实现附加事件附加事件方案处理附加事件定义自定义附加事件引发 WPF 附加事件 Extensible Application Markup Language (XAML) 定义了一种语言组件和称为附加事件的事件类型。 附加事件可用于在非元素类中定义新的 路由事件,…...
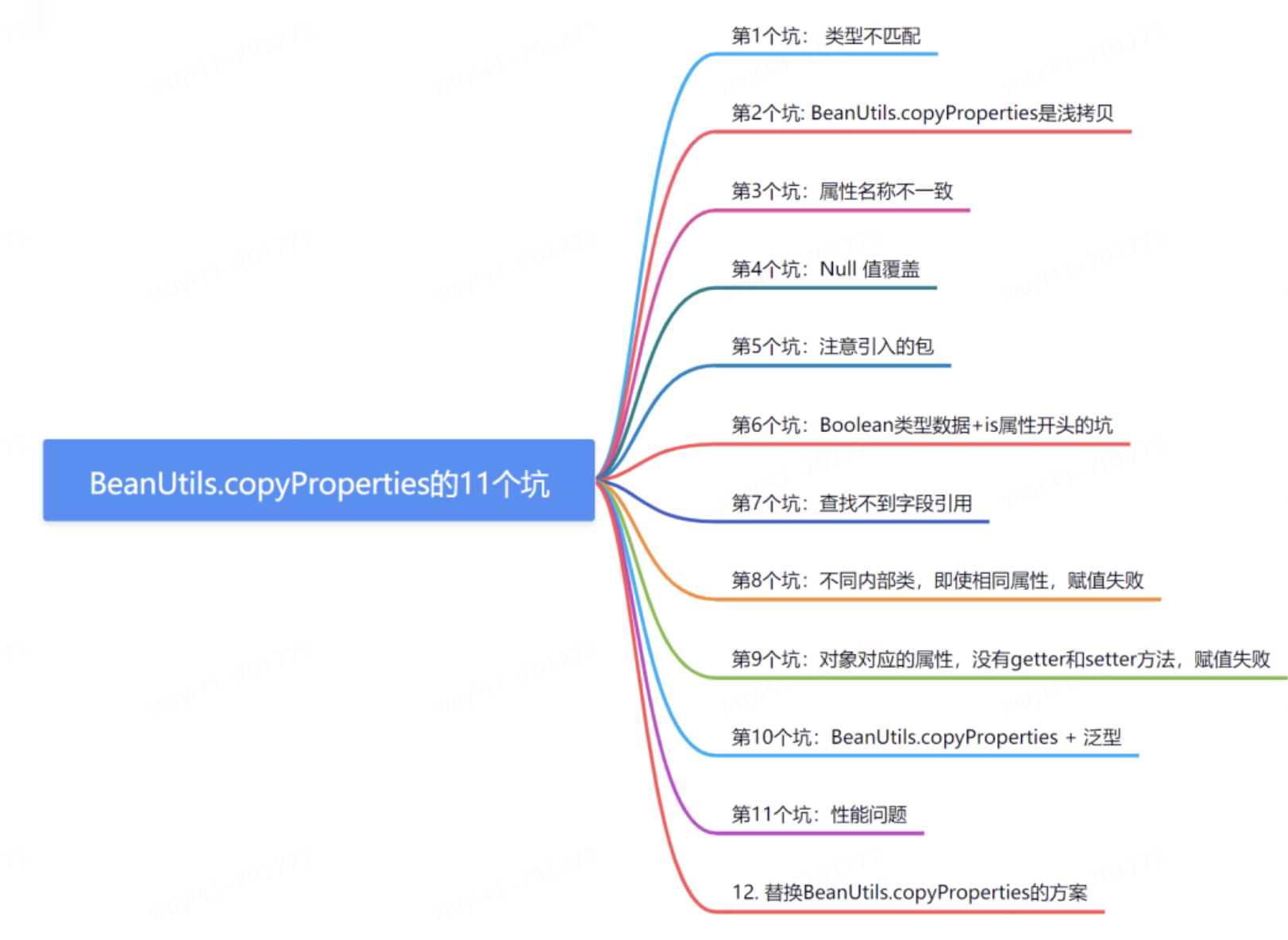
java浅拷贝BeanUtils.copyProperties引发的RPC异常 | 京东物流技术团队
背景 近期参与了一个攻坚项目,前期因为其他流程原因,测试时间已经耽搁了好几天了,本以为已经解决了卡点,后续流程应该顺顺利利的,没想到 人在地铁上,bug从咚咚来~ 没有任何修改的服务接口,抛出…...

【pynput】鼠标行为追踪并模拟
文章目录 前言基本思路安装依赖包实时鼠标捕获捕获鼠标位置捕获鼠标事件记录点击内容效果图 实时按键捕获控制按键操作捕获按键事件组合键记录区间设置 用户操作记录与回溯基本思路完整代码效果图 利用本文内容从事的任何犯法行为和开发与本人无关,请理性利用技术服…...
docker小白第十天
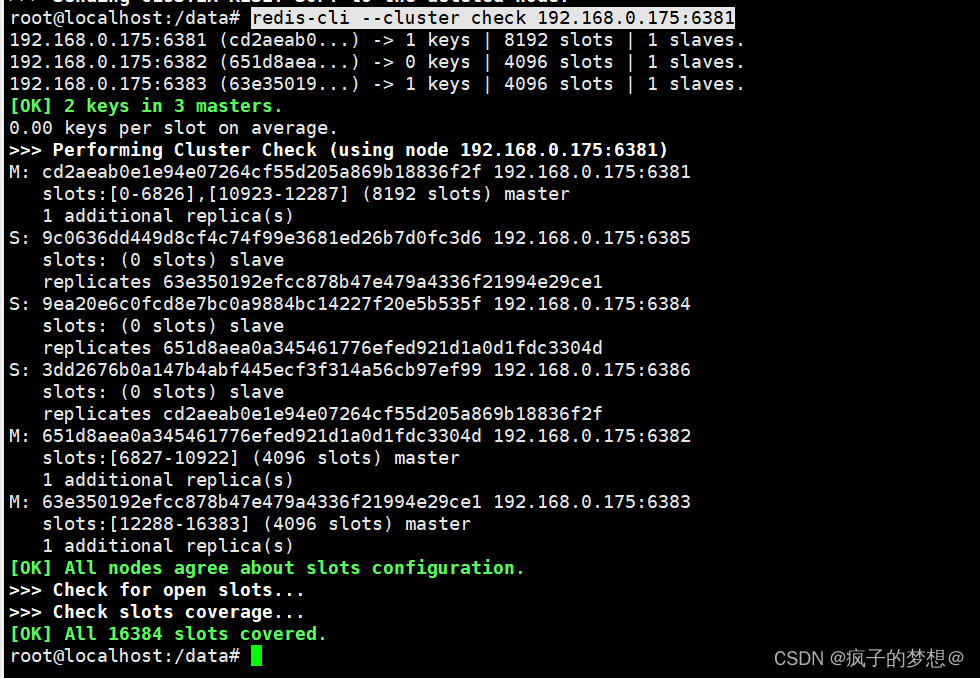
redis集群主从容错切换案例 3主3从的redis集群,某个主机宕机了,需要对应的从机补位。 docker exec -it redis-node-1 /bin/bash # 进入容器1的命令行 redis-cli -p 6381 # 进入节点1的命令行 cluster nodes # 查看集群信息可以看到1号和6号对应是主从关…...
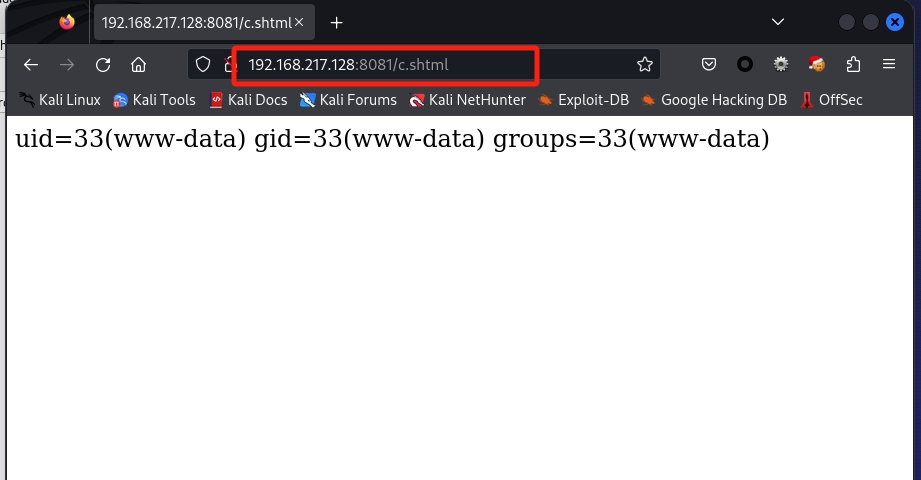
Apache SSI 远程命令执行漏洞
一、环境搭建 二、访问upload.php 三、写shell <!--#exec cmd"id" --> 四、访问 如图所示,即getshell成功!...

阿里云30个公共云地域、89个可用区、5个金融云和政务云地域
阿里云基础设施目前已面向全球四大洲,公共云地域开服运营30个公共云地域、89个可用区,此外还拥有5个金融云、政务云地域,并且致力于持续的新地域规划和建设,从而更好的满足用户多样化的业务和场景需求。伴随着基础设施的加速投入和…...

Linux驱动开发之杂项设备注册和Linux2.6设备注册
目录 一、杂项设备注册 杂项设备注册简介 杂项设备注册特点: 杂项设备注册相关API misc_register() misc_deregister() 杂项设备注册相关例程 例程简介 源码分享 二、Linux 2.6设备注册 Linux2.6设备注册简介 Linux 2.6设备注册特点 Linux2.6设备注册流程 Linu…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
