动态规划 | 最长公共子序列问题
文章目录
- 最长公共子序列
- 题目描述
- 问题分析
- 程序代码
- 复杂度分析
- 最短编辑距离
- 题目描述
- 问题分析
- 程序代码
- 复杂度分析
- 编辑距离
- 题目描述
- 输入格式
- 输出格式
- 问题分析
- 程序代码
最长公共子序列
题目描述
原题链接
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
问题分析
这里假设text1和text2的下标均从 1 开始
状态定义:dp[i][j]表示text1[1...i]和text2[1...j]的最长公共子序列的长度
状态划分:根据text1[i]和text2[j]是否在最长公共子序列中,可以将状态划分为四类
text1[i]在,text1[j]也在:dp[i][j] = dp[i-1][j-1] + 1,同时要求text1[i] == text2[j]text1[i]在,text1[j]不在:dp[i][j] = dp[i][j-1]text1[i]不在,text1[j]在:dp[i][j] = dp[i-1][j]text1[i]不在,text1[j]也不在:dp[i][j] = dp[i-1][j-1]
由于情况 4 包含在情况 2 和情况 3 中,因此不需要要单独考虑,最终可以得到如下的状态计算。
状态计算:
- 若
text1[i] == text2[j]:dp[i][j] = dp[i-1][j-1] + 1 - 若
text1[i] != text2[j]:dp[i][j] = max(dp[i][j-1], dp[i-1][j])
程序代码
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int n = text1.size(), m = text2.size();vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));text1 = ' ' + text1;text2 = ' ' + text2;for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {dp[i][j] = max(dp[i-1][j], dp[i][j-1]);if( text1[i] == text2[j] ) {dp[i][j] = max(dp[i][j], dp[i-1][j-1] + 1);}}}return dp[n][m];}
};
复杂度分析
时间复杂度为 O ( N 2 ) O(N^2) O(N2)
最短编辑距离
题目描述
原题链接
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
问题分析
这里假设word1和word2的下标均从 1 开始
状态定义:dp[i][j]表示将word1[1...i]变成word2[1...j]所需的最少操作次数
状态计算:dp[i][j]可能从三种可能状态转移过来,三种状态取最小值
- 删除操作:删除
word1[i],使得word1和word2匹配,即dp[i][j] = dp[i-1][j] + 1 - 插入操作:在
word1的末尾插入word2[j],使得二者匹配,即dp[i][j] = dp[i][j-1] + 1 - 替换操作:
word1[1...i-1]与word2[1...j-1]匹配,word1[i]和word2[j]有两种情况- 若
word1[i] == word2[j],则无需进行替换操作,即dp[i][j] = dp[i-1][j-1] - 若
word1[i] != word2[j],则需进行替换操作,即dp[i][j] = dp[i-1][j-1] + 1
- 若
边界情况:
dp[0][0]:二者都为空,无需进行任何操作,即dp[0][0] = 0dp[0][i]:表示word1为空,word1只能通过插入操作变成word2,即dp[0][i] = idp[i][0]:表示word2为空,word1只能通过删除操作变成word2,即dp[i][0] = i
程序代码
class Solution {
public:int minDistance(string word1, string word2) {int n = word1.size(), m = word2.size();int maxVal = m + n; // 初始化数组word1 = ' ' + word1;word2 = ' ' + word2;vector<vector<int>> dp(n + 1, vector<int>(m + 1, maxVal));// 边界情况dp[0][0] = 0;for(int i = 1; i <= m; i++) {dp[0][i] = i;}for(int i = 1; i <= n; i++) {dp[i][0] = i;}for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {// 删除和插入操作dp[i][j] = min(dp[i-1][j] + 1, dp[i][j-1] + 1);// 替换操作if(word1[i] == word2[j]) {dp[i][j] = min(dp[i][j], dp[i-1][j-1]);}else {dp[i][j] = min(dp[i][j], dp[i-1][j-1] + 1);}}}return dp[n][m];}
};
复杂度分析
时间复杂度为 O ( N 2 ) O(N^2) O(N2)
编辑距离
题目描述
给定 n 个长度不超过 10 的字符串以及 m 次询问,每次询问给出一个字符串和一个操作次数上限。
对于每次询问,请你求出给定的 n 个字符串中有多少个字符串可以在上限操作次数内经过操作变成询问给出的字符串。
每个对字符串进行的单个字符的插入、删除或替换算作一次操作。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含一个字符串,表示给定的字符串。
再接下来 m 行,每行包含一个字符串和一个整数,表示一次询问。
字符串中只包含小写字母,且长度均不超过 10。
输出格式
输出共 m 行,每行输出一个整数作为结果,表示一次询问中满足条件的字符串个数。
问题分析
本质上其实就是最短编辑距离问题
程序代码
#include <iostream>
#include <algorithm>
using namespace std;int n, m;
const int N = 1010, INF = 1e9 + 7;
string s[N];
string p;
int k;int solve(string a, string b)
{int n = a.size(), m = b.size();a = ' ' + a;b = ' ' + b;vector<vector<int>> dp(n + 1, vector<int>(m + 1, INF));// 边界情况dp[0][0] = 0;for(int i = 1; i <= m; i++) {dp[0][i] = i;}for(int i = 1; i <= n; i++) {dp[i][0] = i;}for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {// 删除和插入操作dp[i][j] = min(dp[i-1][j] + 1, dp[i][j-1] + 1);// 替换操作if(a[i] == b[j]) {dp[i][j] = min(dp[i][j], dp[i-1][j-1]);}else {dp[i][j] = min(dp[i][j], dp[i-1][j-1] + 1);}}}return dp[n][m];
}int main()
{cin >> n >> m;for(int i = 0; i < n; i++) {cin >> s[i];}for(int i = 0; i < m; i++) {cin >> p >> k;int cnt = 0;for(int j = 0; j < n; j++) {if( solve(s[j], p) <= k ) cnt++;}printf("%d\n", cnt);}return 0;
}
相关文章:

动态规划 | 最长公共子序列问题
文章目录 最长公共子序列题目描述问题分析程序代码复杂度分析 最短编辑距离题目描述问题分析程序代码复杂度分析 编辑距离题目描述输入格式输出格式 问题分析程序代码 最长公共子序列 题目描述 原题链接 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共…...

RuntimeError: The NVIDIA driver on your system is too old.
【报错】使用 AutoDL 复现实验时遇到 RuntimeError: The NVIDIA driver on your system is too old (found version 11070). Please update your GPU driver by downloading and installing a new version from the URL: http://www.nvidia.com/Download/index.aspx Alternativ…...
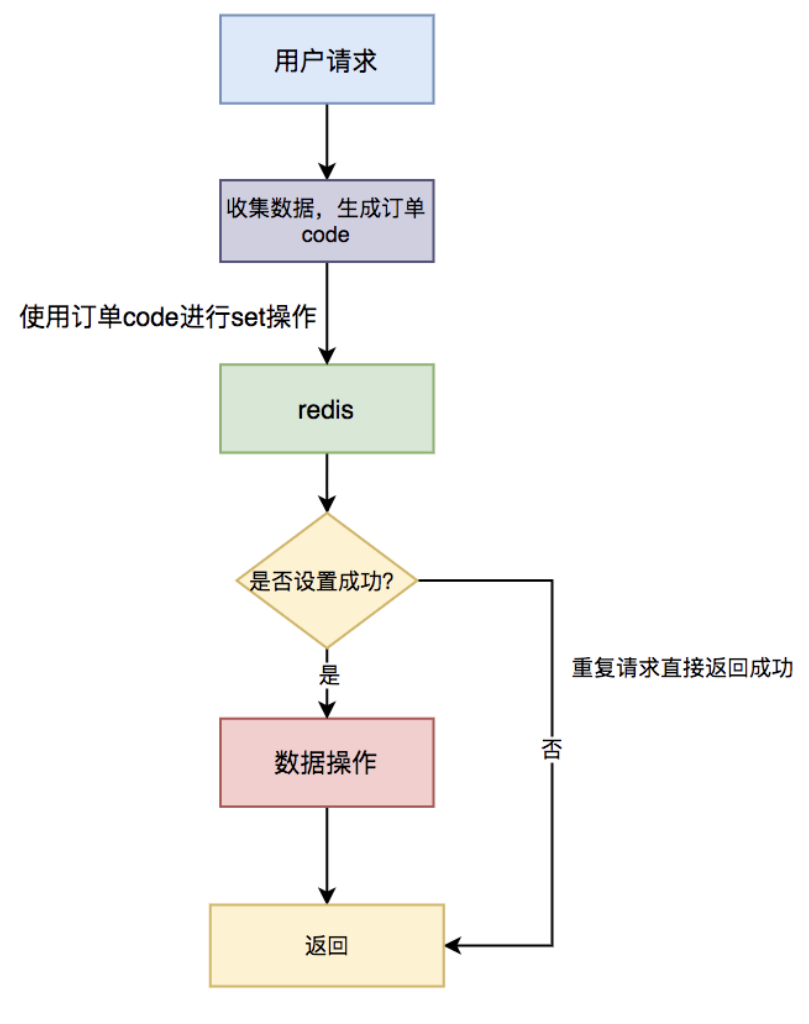
Java开发过程中的幂等性问题
幂等性问题: 1. 有时我们在填写某些 form表单 时,保存按钮不小心快速点了两次,表中竟然产生了两条重复的数据,只是id不一样。 2. 我们在项目中为了解决 接口超时 问题,通常会引入了 重试机制 。第一次请求接口超时了…...

基于Docker的软件环境部署脚本,持续更新~
使用时CtrlF搜索你想要的环境,如果没有你想要的环境,可以评论留言,会尽力补充。 本文提供的部署脚本默认参数仅适合开发测试,请根据实际情况调节参数。 数据库 MySQL version: 3.9 services:mysql:image: mysql:8.0.35container…...

C#上位机与欧姆龙PLC的通信08----开发自己的通讯库读写数据
1、介绍 前面已经完成了7项工作: C#上位机与欧姆龙PLC的通信01----项目背景-CSDN博客 C#上位机与欧姆龙PLC的通信02----搭建仿真环境-CSDN博客 C#上位机与欧姆龙PLC的通信03----创建项目工程-CSDN博客 C#上位机与欧姆龙PLC的通信04---- 欧姆龙plc的存储区 C#上…...
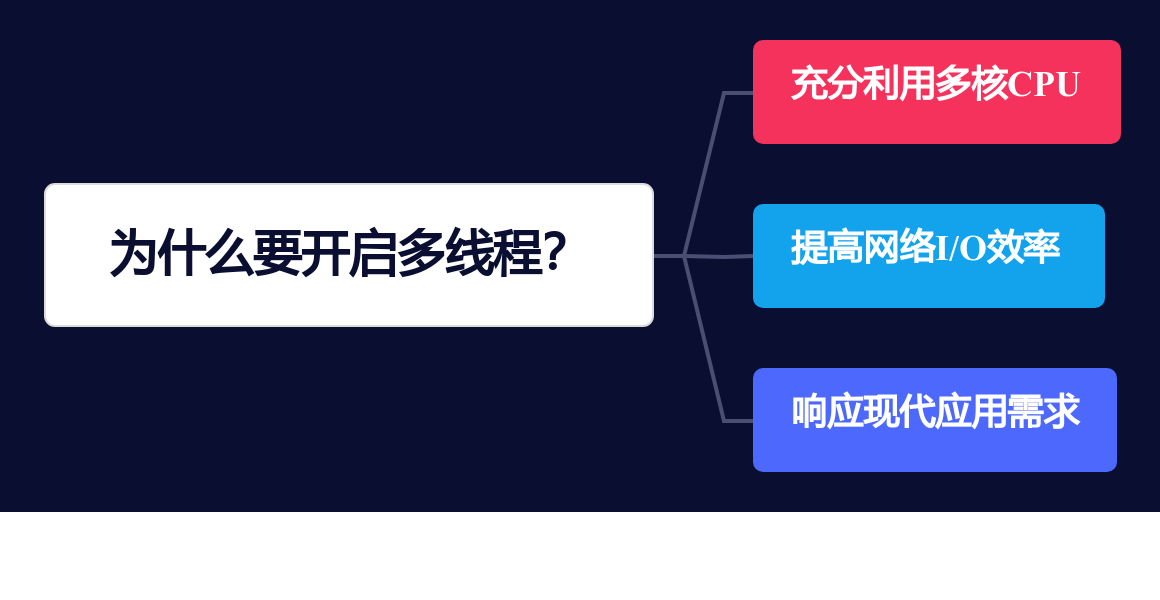
【Redis技术专区】「原理分析」探讨Redis6.0为何需要启用多线程
探讨Redis 6.0为何需要启用多线程 背景介绍开启多线程多线程的CPU核心配置IO多线程模式单线程处理方式多线程处理方式 为什么要开启多线程?充分利用多核CPU提高网络I/O效率响应现代应用需求 多线程实现启用多线程 最后总结 背景介绍 在Redis 6.0版本中,…...
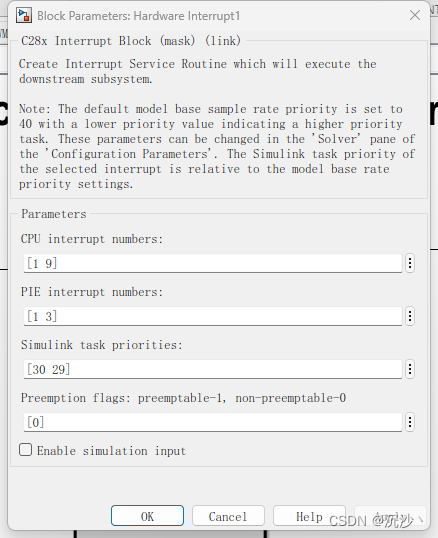
simulink代码生成(六)——多级中断的配置
假如系统中存在多个中断,需要合理的配置中断的优先级与中断向量表;在代码生成中,要与中断向量表对应;中断相关的知识参照博客: DSP28335学习——中断向量表的初始化_中断向量表什么时候初始化-CSDN博客 F28335中断系…...
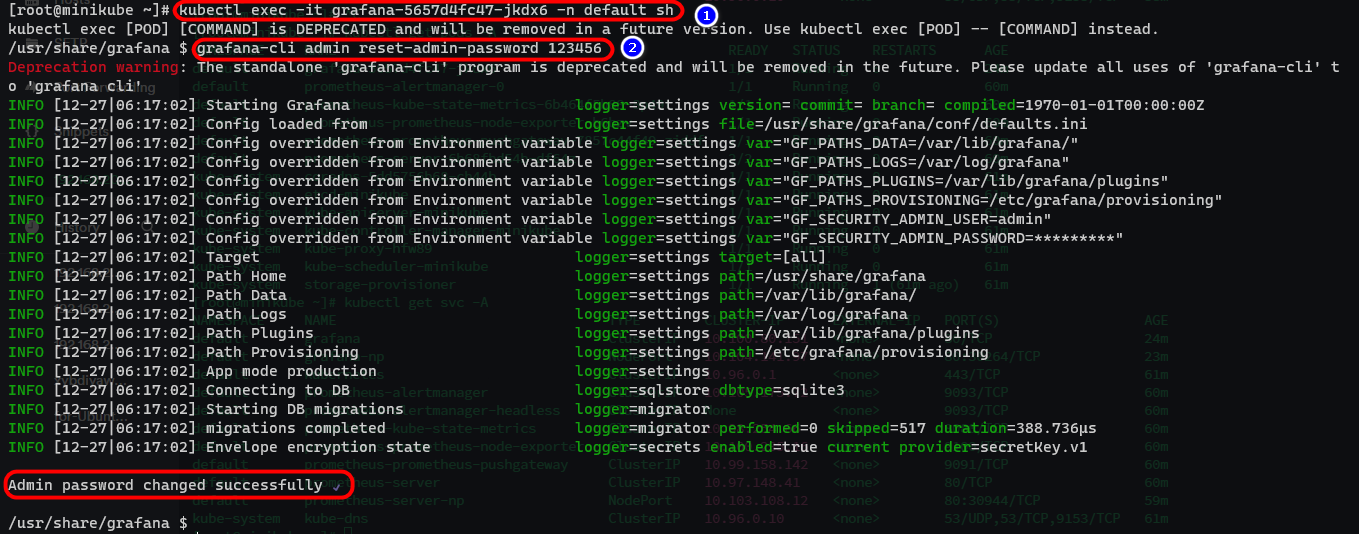
【Minikube Prometheus】基于Prometheus Grafana监控由Minikube创建的K8S集群
文章目录 1. 系统信息参数说明2. Docker安装3. minikube安装4. kubectl安装5. Helm安装6. 启动Kubernetes集群v1.28.37. 使用helm安装Prometheus8. 使用helm安装Grafana9. Grafana的Dashboard设定10. 设定Prometheus数据源11. 导入Kubernetes Dashboard12. 实验过程中的常见问题…...

无需翻墙|Stable Diffusion WebUI 安装|AI绘画
前言 最近终于有机会从围墙里往外看,了解到外面的世界已经有了天翻地覆的变化,感叹万千,笔者在本地mac,windows,linux,docker部署了不下20遍后,整理出来的linux极简避坑安装方案,供…...
在FC中手工创建虚拟机模板
1、Linux去除个性化信息 (1)编辑网卡配置文件,只保留以下内容(以RHEL 7为例) (2)清除主机密钥信息(开机会自动生成) (3)清除Machine IDÿ…...

OpenSSL provider
提供者 标准提供者默认提供者传统提供者FIPS 提供者基本提供者空提供者加载提供者 标准提供者 提供者是算法实现的容器。每当通过高级别 API 使用加密算法时,都会选择一个提供者。实际上是由该提供者实现执行所需的工作。OpenSSL 自带了五个提供者。在未来&#…...

pandas处理双周数据
处理文件题头格式 部门名称 年度名称 季节名称 商品名称 商品代码 品牌名称 品类名称 颜色名称 商店名称 0M 1L 1XL 27 28 29 2XL 30 31 32 33 3XL 4XL 5XL 6XL S 均1.导入包 导入源 pip install openpyxl -i https://pypi.doubanio.com/simple pip install pandas -i https…...
2023结婚成家,2024借势起飞
您好,我是码农飞哥(wei158556),感谢您阅读本文,欢迎一键三连哦。 💪🏻 1. Python基础专栏,基础知识一网打尽,9.9元买不了吃亏,买不了上当。 Python从入门到精…...
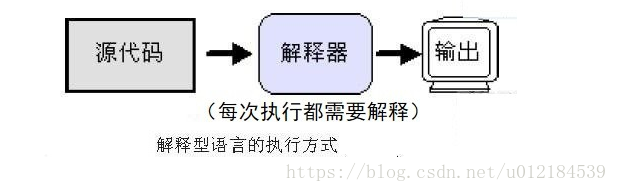
linux SHELL语句
shell编程 shell编程 一、初识shell 程序 语言 编程语言 自然语言 汉语 英语 计算机语言 c语言cjava php python go shell 编译型语言 c c java解释型语言 php python bash (不能闭源,开发难度低) 编译型语言:运行编译型语言是相对于解释型语言存在的ÿ…...
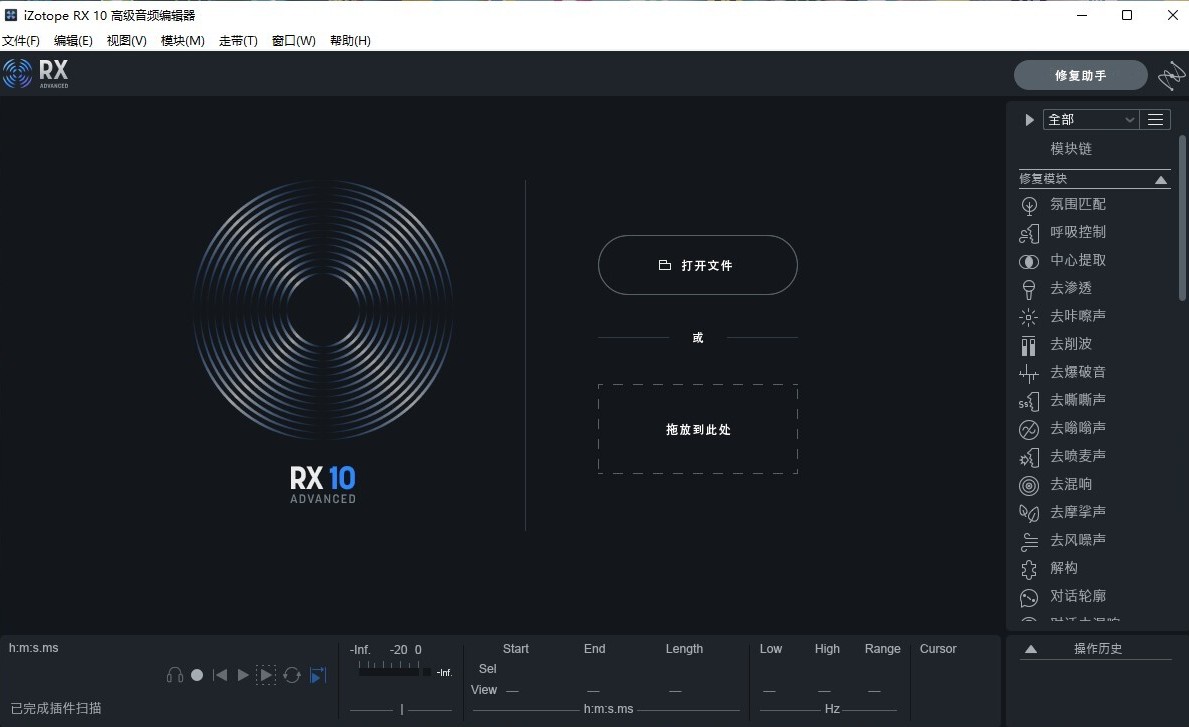
音频修复和增强软件:iZotope RX 10 (Win/Mac)中文汉化版
iZotope RX 是一款专业的音频修复和增强软件,一直是电影和电视节目中使用的行业标准音频修复工具,iZotope能够帮助用户对音频进行制作、后期合成处理、混音以及对损坏的音频进行修复,再解锁更多功能之后还能够对电影、游戏、电视之中的音频进…...
算法篇)
复试 || 就业day03(2023.12.29)算法篇
文章目录 前言同构字符串存在重复元素有效的字母异位词丢失的数字单词规律 前言 💫你好,我是辰chen,本文旨在准备考研复试或就业 💫文章题目大多来自于 leetcode,当然也可能来自洛谷或其他刷题平台 💫欢迎大…...
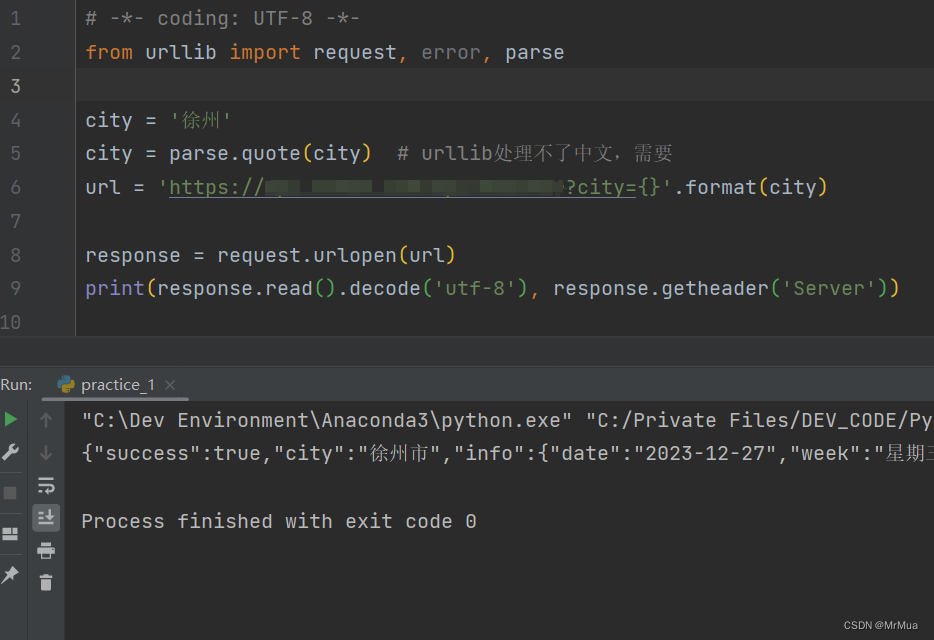
处理urllib.request.urlopen报错UnicodeEncodeError:‘ascii‘
参考:[Python3填坑之旅]一urllib模块网页爬虫访问中文网址出错 目录 一、报错内容 二、报错截图 三、解决方法 四、实例代码 五、运行截图 六、其他UnicodeEncodeError: ascii codec 问题 一、报错内容 UnicodeEncodeError: ascii codec cant encode charac…...
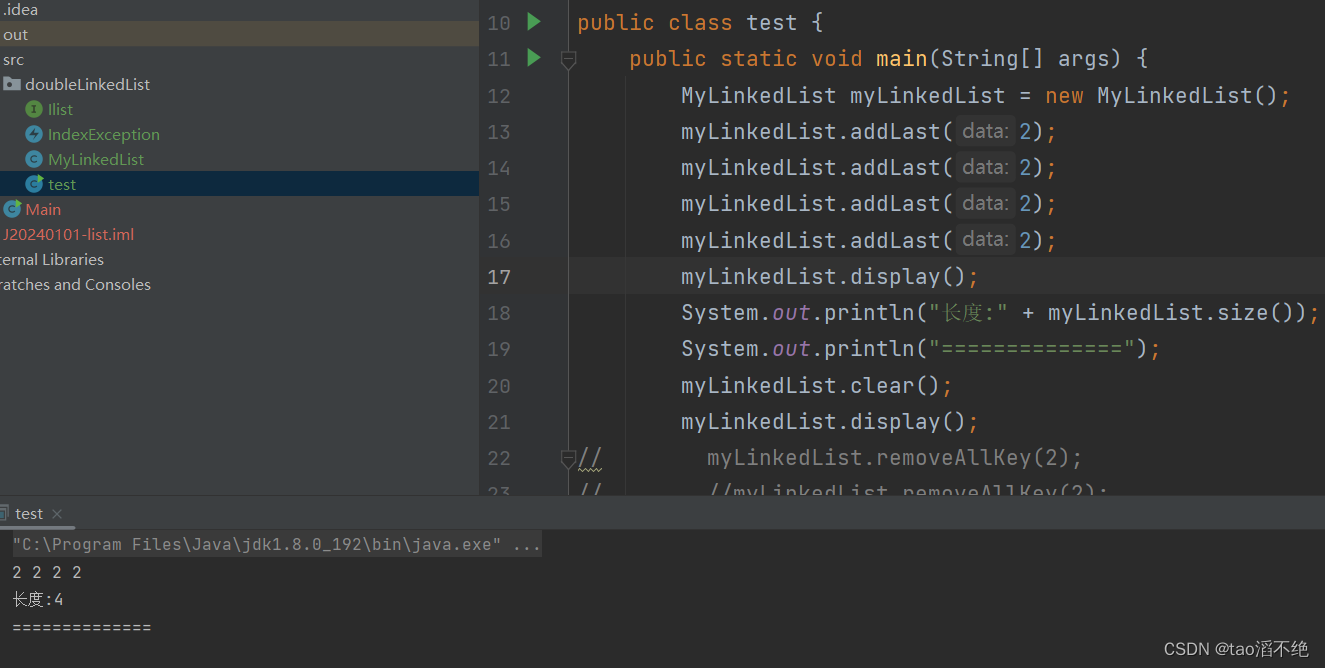
数据结构模拟实现LinkedList双向不循环链表
目录 一、双向不循环链表的概念 二、链表的接口 三、链表的方法实现 (1)display方法 (2)size方法 (3)contains方法 (4)addFirst方法 (5)addLast方法 …...
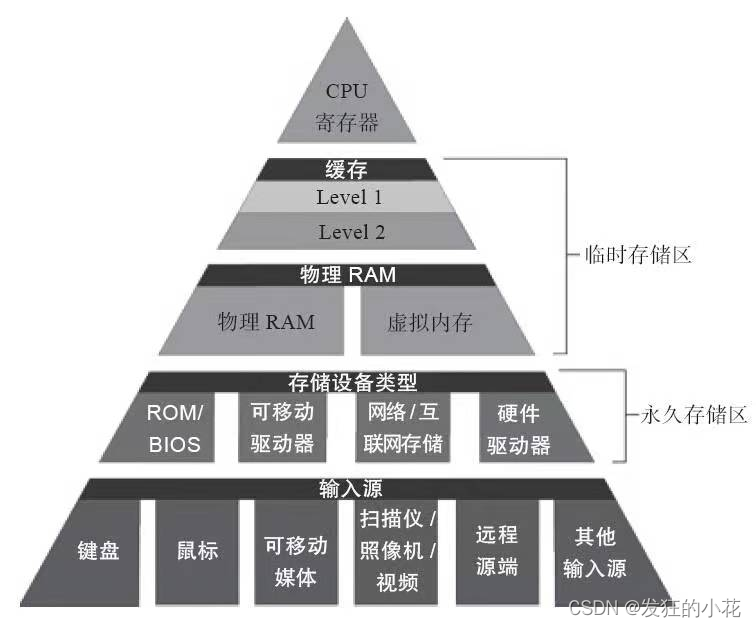
性能优化-如何提高cache命中率
本文主要介绍性能优化领域常见的cache的命中率问题,旨在全面的介绍提高cache命中率的方法,以供大家编写出性能友好的代码,并且可以应对性能优化领域的面试问题。 🎬个人简介:一个全栈工程师的升级之路! &am…...

分布式【4. 什么是 CAP?】
什么是 CAP? C 代表 Consistency,一致性,是指所有节点在同一时刻的数据是相同的,即更新操作执行结束并响应用户完成后,所有节点存储的数据会保持相同。 A 代表 Availability,可用性,是指系统提…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
