Codeforces Round 900 (Div. 3)(A-F)
比赛链接 :
Dashboard - Codeforces Round 900 (Div. 3) - Codeforces
A. How Much Does Daytona Cost?
题面 :

思路 :
在序列中只要找到k,就返回true ;
代码 :
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;
typedef long long LL;
const int N = 2e5+10;inline void solve(){int n , k ; cin >> n >> k ;bool tag = false;for(int i=0;i<n;i++){int x ; cin >> x ;if(x==k) tag = true;}if(tag) cout << "Yes" << endl;else cout << "No" << endl;return ;
}int main()
{IOSint _ = 1;cin >> _;while(_ --) solve();return 0;
}B. Aleksa and Stack
题面 :

思路 :
在这道题中,只要满足任意两个相邻数的和,不能够不是3的倍数,且数组单调递增,那么便可以构造出这样一个序列,每两个相邻数中第一个数 mod 3 = 0,另一个数mod 3 = 1 ,然后递增的话,就可以使a1 = 3 *1 , a2= a1 + 1,a3 = 3 * 2,a4 = a3 + 1,即可满足题目条件;
代码
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;
typedef long long LL;
int gcd(int a,int b){ return b==0 ? a : gcd(b,a%b); }
int lcm(int a,int b){ if(a==0||b==0) return 0; return (a*b)/gcd(a,b); }
bool is_prime(int x){if(x<2) return false;
for(int i=2;i<=x/i;i++) if(x%i==0) return false; return true;}
//numbers.erase(std::unique(numbers.begin(), numbers.end()), numbers.end()); // 去重操作
const int N = 2e5+10;// 任意两个数的和不是3的倍数 // 0, 1, 2
// 3 , 4 , 6, 7 inline void solve(){int n ; cin >> n ;int x = 3;while(n>1){cout << x << " " << x + 1 << " ";x += 3;n -= 2;}if(n) cout << x ;cout << endl ;return ;}int main()
{IOSint _ = 1;cin >> _;while(_ --) solve();return 0;
}C. Vasilije in Cacak
题面 :
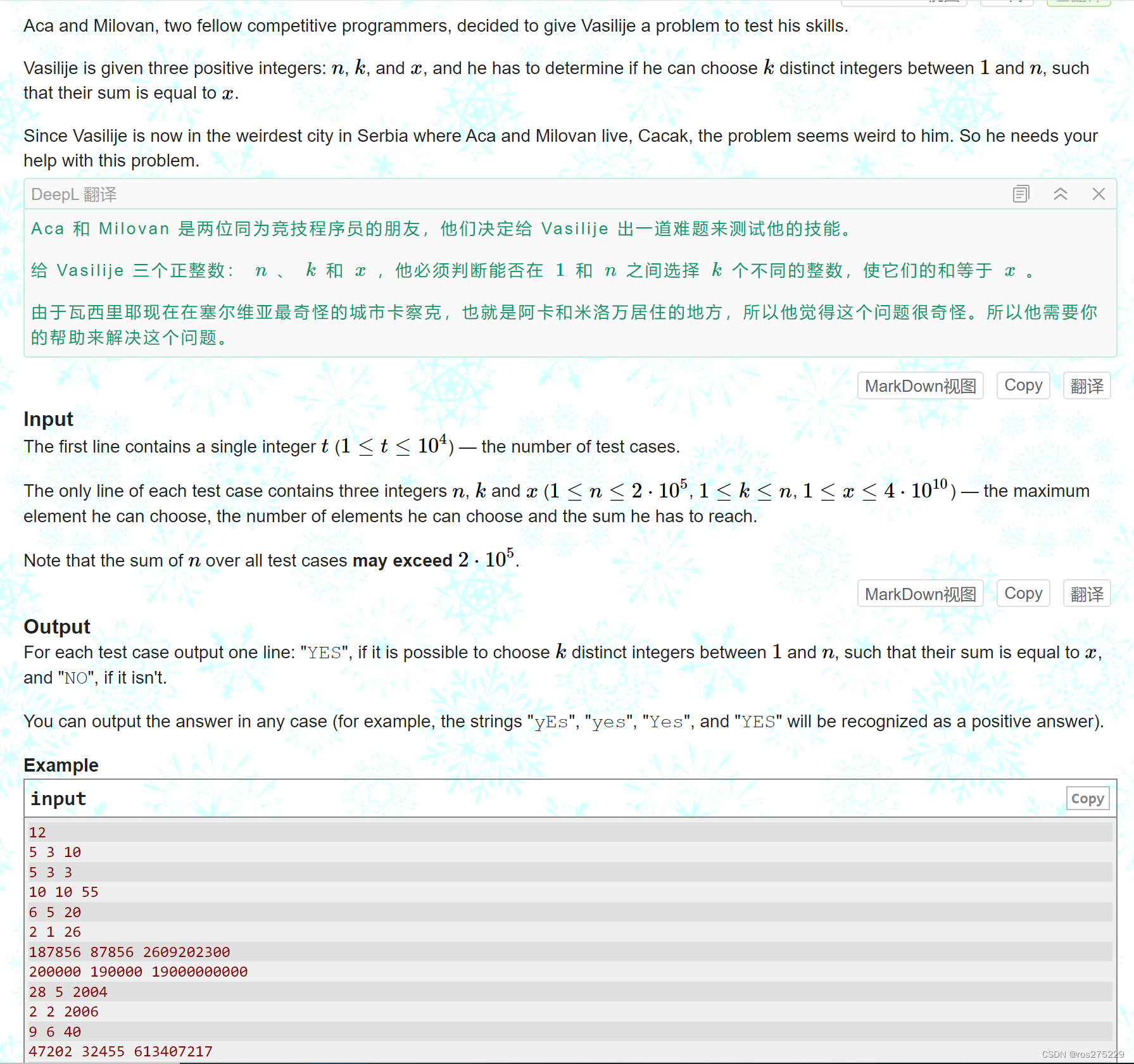
思路 :
对于从 [1 ,n ] 中 选k个数 的 和为x;
假如 n = 2 (并且假设k = 2,下面一样):
1,2 --> 1, 2, 3
n = 3 :
1, 2 ,3 : 1,2,3,4,5,6 选两个 : 3-5
n = 4 :
1,2,3,4 : 3-7 :
那么我们就可以发现一个规律 : 在[1,n]中取k个数和的范围是[最小的k个数相加,最大的k个数相加];
为了计算的方便,我们可以使用等差数列求和 : s = n*a1+(n-1)*n*d/2 ;
代码 :
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;
typedef long long LL;LL n , k , x ;// [1,n] 中 选k个数 的 和为x;// 1,2 --> 1, 2, 3
//1, 2 ,3 : 1,2,3,4,5,6 选两个 : 3-5
// 1,2,3,4 : 3-7 : // 等差数列求和 : s = n*a1+(n-1)*n*d/2 inline void solve(){cin >> n >> k >> x;LL l = (1+k)*k/2 , r = (n+n-k+1)*k/2;if(x>=l && x<=r) cout << "Yes" << endl;else cout << "No" << endl;return ;
}int main()
{IOSint _ = 1;cin >> _;while(_ --) solve();return 0;
}D. Reverse Madness
题面

思路 :
l和r都是单调递增的,且对于每一段区间都是不相交的,所有可以很快找到x对应的li和ri来满足li<=x && x<=ri ;
找到之后就是进行区间的反转,对于每个区间假设li = 2,ri =6,如果x = 4,则a=b=4,如果x=3,则a=3,b=5;那么说明是关于终点对称的,那么就可以使用前缀和算法,来对每个点进行反转次数的统计,如果统计次数为偶那就不用反转了,为奇,则要反转,具体请看代码;
代码
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;
typedef long long LL;
const int N = 2e5+10;inline void solve(){int n,k;cin >> n >> k ;string s ; cin >> s ;s = ' ' + s ;vector<int> l(k+1) , r (k+1) ;for(int i=1;i<=k;i++) cin >> l[i] ;for(int i=1;i<=k;i++) cin >> r[i] ;int q ; cin >> q ;vector<int> x(q+1) ;for(int i=1;i<=q;i++) cin >> x[i] ;vector<pair<int,int>> sum(n+3) ;for(int i=1;i<=q;i++){int pos = lower_bound(r.begin()+1,r.end(),x[i]) - r.begin();int a = min(x[i] , r[pos]+l[pos]-x[i]);int b = max(x[i],r[pos]+l[pos]-x[i]);sum[a].first++ ; sum[b+1].first--;sum[a].second = b ; sum[b].second = a ;}for(int i=1;i<n;i++){sum[i].first += sum[i-1].first ;}int start = -1 , end = -1 ;for(int i=1;i<=n;i++){if(sum[i].first % 2 == 1){start = i ;int end = sum[i].second ;while(start <= end){while(start<=end && sum[start].first % 2 == 1){swap(s[start],s[end]);start ++;end--;}while(start <= end && sum[start].first % 2 == 0){start ++;end -- ;}}i = sum[i].second ;}}for(int i=1;i<=n;i++) cout << s[i] ;cout << endl;
}int main()
{IOSint _ = 1;cin >> _;while(_ --) solve();return 0;
}E. Iva & Pav
题面 :

思路 :
// f(l,r)=al & al+1 &…& ar
// 给定一个 l , k ,求最大的r,满足f(l , r) >= k ;
// 定l,则f随着r单调递减
// & : 按位与
按位与的特点是,对于某一位,[l,r]上的所有数的该位上为1,结果才为1,那么我们可以采用前缀和的思想,用bit[i][j]来存[1,i]上第j位上为1的个数,具体实现请看代码,再获得bit数组之后,因为在l确定之后,f(l,r)随着r的增大具有单调递减的性质,所有可以使用二分来进行操作;
具体实现请看代码 ;
代码 :
// f(l,r)=al & al+1 &…& ar
// 给定一个 l , k ,求最大的r,满足f(l , r) >= k ;
// 定l,则f随着r单调递减
// & : 按位与
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;
typedef long long LL;
const int N = 2e5 + 10 ;inline void solve(){int n ; cin >> n ;vector<array<int,32>> bit(n+1);for(int i=1;i<=n;i++){int x ; cin >> x ;for(int j = 0;j<32;j++){bit[i][j] = 0 ;bit[i][j] += x % 2 ;x /= 2 ;bit[i][j] += bit[i-1][j] ; // 进行前缀和操作,统计i前面j位上为1的个数 } } auto check = [&](int l,int r ,int c){vector<int> b(32) ;for(int i=0;i<32;i++){b[i] = bit[r][i] - bit[l-1][i] ;}int ans = 0 ;for(int i=0;i<32;i++){if(b[i]==r-l+1) ans += pow(2,i);}return ans >= c ; };int q ; cin >> q ;while(q--){int l , k ; cin >> l >> k ;int L = l, R = n;int ans = -1 ;while(L<=R){int mid = (L+R)>>1 ;if(check(l,mid,k)){ans = mid ;L = mid + 1; }else{R = mid - 1 ;}}cout << ans << " " ;}cout << endl ;
}int main()
{IOSint _ = 1;cin >> _;while(_ --) solve();return 0;
}F. Vasilije Loves Number Theory
题面 :

思路 :
- 1 : n *= x,然后问是否存在一个a使得gcd(n,a)=1并且n*a的约数个数等于n,
- gcd(n,a)=1 --> n,a互质
- 由于n,a互质,那么 d(n)*d(a)=d(n*a),那么就是要d(a) = n / d(n),所以n % d(n)一定要等于零
然后就可以通过唯一分解定理来解;
具体实现请看代码 :
代码
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;
typedef long long LL;
const int N = 2e5+10;// 1 : n *= x,然后问是否存在一个a使得gcd(n,a)=1并且n*a的约数个数等于n,
// gcd(n,a)=1 --> n,a互质
// --> d(n)*d(a)=d(n*a),那么就是要d(a) = n / d(n),所以n % d(n)一定要等于零 inline void solve(){int n,q;cin>>n>>q;int cnt = 1 ; // 记录因数的数量 map<int,int> doc ;// 质因数分解 : // num = b1^c1 + b2 ^c2 + .... + bn^cn ; for(int i=2;i*i<=n;i++){// i相当于上面的b,c相当于上面的c ; if(n%i==0){int c = 0 ;while(n%i==0) n/=i,c++;doc[i] = c ;cnt *= (c+1);}}if(n>1) doc[n] = 1 , cnt *= 2 ; // 最后剩下的n本身也是一个质因数 int now = cnt;auto doc2 = doc ;while(q--){int op ; cin >> op ;if(op == 2){now = cnt ;doc2 = doc ;}else{int x ; cin >> x ;for(int i=2;i*i<=x;i++){if(x%i==0){int c = 0 ;while(x%i==0) x/=i,c++;now /= (doc2[i]+1);doc2[i] += c; now *= (doc2[i]+1);}}if(x>1){now /= (doc2[x]+1);doc2[x]+=1;now *= (doc2[x]+1);}int t = now ;for(auto it:doc2){int x = it.first ;int y = it.second ;while(y>0 && t % x== 0){t /= x ;y -- ;}}cout << (t==1?"YES":"NO")<<endl; }}
}int main()
{IOSint _ = 1;cin >> _;while(_ --) solve();return 0;
}相关文章:

Codeforces Round 900 (Div. 3)(A-F)
比赛链接 : Dashboard - Codeforces Round 900 (Div. 3) - Codeforces A. How Much Does Daytona Cost? 题面 : 思路 : 在序列中只要找到k,就返回true ; 代码 : #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)…...

vue大屏-列表自动滚动vue-seamless-scroll
vue大屏-列表自动滚动vue-seamless-scroll vue-seamless-scroll的官方文档地址:https://chenxuan0000.github.io/vue-seamless-scroll/zh/guide/ 具体效果可到官方文档那里查看。 1、下载依赖 npm install vue-seamless-scroll --save2、使用例子 <template…...
easyx的窗口函数
文章目录 前言一、EasyX的颜色二、EasyX的坐标和设备1,EasyX的坐标2,EasyX的设备 三、窗口函数1,初始化窗口函数2,关闭绘图窗口3,设置窗口背景板颜色4,清空绘图设备 前言 easyx是针对c的图形库,…...

【记录】开始学习网络安全
本文持续更新学习进度 背景 在私企干了5年虚拟化、云原生相关的运维,学到了很多,但不成体系。老板是清华毕业法国留学在德勤干过,最后回国创业的野路子。我工作是为了更好的生活,我挺担心老板因为家庭变故或者炒个原油宝&#x…...
【Java EE初阶三 】线程的状态与安全(下)
3. 线程安全 线程安全:某个代码,不管它是单个线程执行,还是多个线程执行,都不会产生bug,这个情况就成为“线程安全”。 线程不安全:某个代码,它单个线程执行,不会产生bug,…...

MD5算法
一、引言 MD5(Message-Digest Algorithm 5)是一种广泛应用的密码散列算法,由Ronald L. Rivest于1991年提出。MD5算法主要用于对任意长度的消息进行加密,将消息压缩成固定长度的摘要(通常为128位)。在密码学…...

Postman使用
Postman使用 Pre-request Script 参考: Scripting in Postman 可以请求、集合或文件夹中添加Pre-request Script,在请求运行之前执行JavaScript 如设置变量值、参数、Header和正文数据,也可以使用Pre-request Script来调试代码࿰…...

【python 的各种模块】(8) 在python使用matplotlib和wordcloud库来画wordcloud词云图
目录 目标:用python画出,网上流行的wordcloud词云图 1 准备工作 1.1环境准备 1.1.1安装步骤 1.2 资源准备 1.2.1 文本文件内容如下 1.2.2 图片资源 2 代码测试 2.1 第一版代码和效果 2.1.1 代码和效果 2.1.2 一般plt里解决中文乱码问题 2.1…...
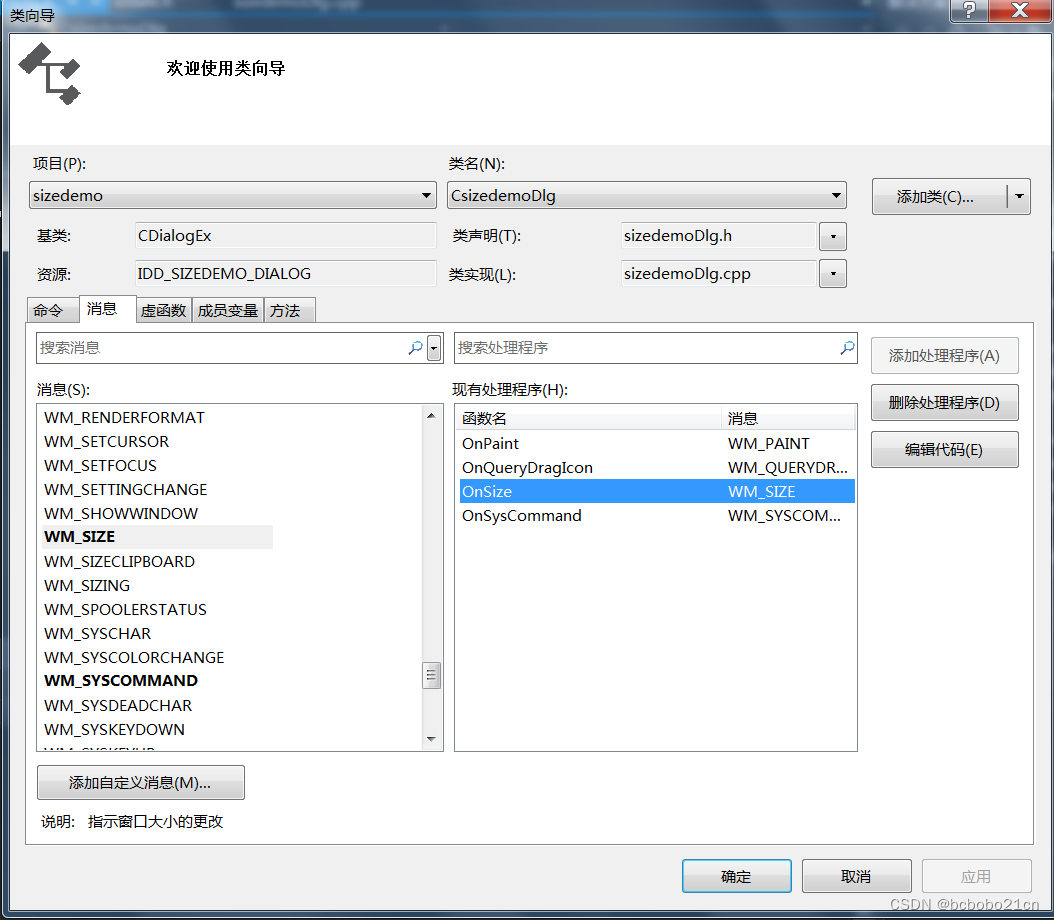
MFC随对话框大小改变同时改变控件大小
先看一下效果; 初始; 窗口变大,控件也变大; 二个也可以; 窗口变大,控件变大; 默认生成的对话框没有WM_SIZE消息的处理程序;打开类向导,选中WM_SIZE消息,对CxxxDlg类添加该消息的处理程序;默认生成的函数名是OnSize; 添加了以后代码中会有三处变化; 在对话框类的…...

MK米客方德品牌 SD NAND在对讲机领域的引领作用
SD NAND在对讲机上的应用 SD NAND在对讲机上广泛应用,为其提供了高效可靠的存储解决方案。 这种存储技术不仅能容纳大量语音和数据文件,而且具有高速读取的特点,保障了实时通信的质量。SD NAND还注重安全性,通过数据加密和访问控…...

软件测试/测试开发丨Python 封装 学习笔记
封装的概念 封装(Encapsulation) 隐藏:属性和实现细节,不允许外部直接访问暴露:公开方法,实现对内部信息的操作和访问 封装的作用 限制安全的访问和操作,提高数据安全性可进行数据检查&#x…...

Vue: 事件修饰符, 键盘事件, 鼠标事件,计算属性
目录 事件修饰符 阻止默认事件 阻止冒泡 允许触发一次 捕获模式 self passive 键盘事件 keyup & keydown 按键别名 注意tab 注意系统按键 自定义按键 鼠标事件 简介 鼠标焦点事件 计算属性 差值语法实现 methods实现 computed实现 get() set() 总…...
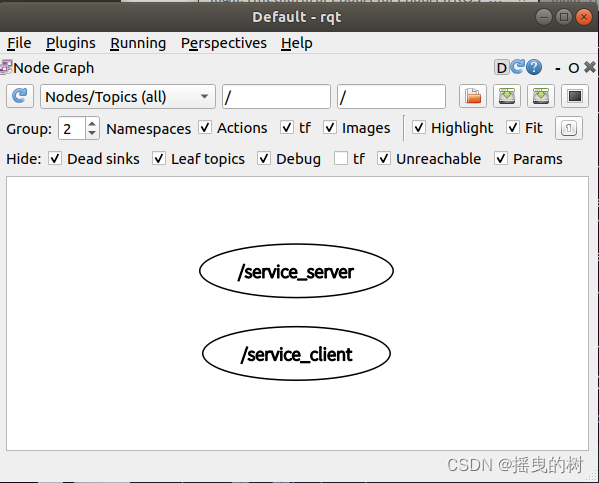
【ROS2】MOMO的鱼香ROS2(四)ROS2入门篇——ROS2节点通信之话题与服务
ROS2节点通信之话题与服务点 引言1 理解从通信开始1.1 TCP(传输控制协议)1.2 UDP(用户数据报协议)1.3 基于共享内存的IPC方式 2 ROS2话题2.1 ROS2话题指令2.2 话题之RCLPY实现2.2.1 编写发布者2.2 2 编写订阅者2.2.3 运行测试 3 R…...

2022年山东省职业院校技能大赛高职组云计算赛项试卷第三场-公有云
2022年山东省职业院校技能大赛高职组云计算赛项试卷 目录 2022年职业院校技能大赛高职组云计算赛项试卷 【赛程名称】云计算赛项第三场-公有云 【任务1】公有云服务搭建[10分] 【适用平台】华为云 【题目1】私有网络管理[0.5分] 【题目2】云实例管理[0.5分] 【题目3】数…...
现代 NLP:详细概述,第 1 部分:transformer
阿比吉特罗伊 一、说明...

记一次Mac端mysql重置密码
在执行mysql命令的时候,报如下的错误,表示不支持mysql命令: zsh: command not found: mysql 1. 先查看mysql服务是否存在 在系统偏好设置中查看: 2. 发现mysql服务已经在运行,可能因为/usr/local/bin目录下缺失mysq…...

【开题报告】基于java的流浪之家动物领养网站的设计与开发
1.选题背景 流浪之家动物领养网站的设计与开发背景主要源于对流浪动物保护和宠物领养问题的关注。随着城市化进程加快,越来越多的流浪动物出现在城市中,它们面临着食物、住所和医疗资源的缺乏。同时,许多爱心人士希望能够给流浪动物一个温暖…...

训狗技术从初级到高级,专业有效的训狗训犬教程
一、教程描述 现在大部分人家里都会养些宠物,比如狗狗,虽然狗狗的一些行为习惯跟遗传有关,但是主人后天的影响也会给狗狗带来改变,本套教程教你纠正狗狗的不良行为,可以让你与狗愉快地玩耍。本套训狗教程,…...
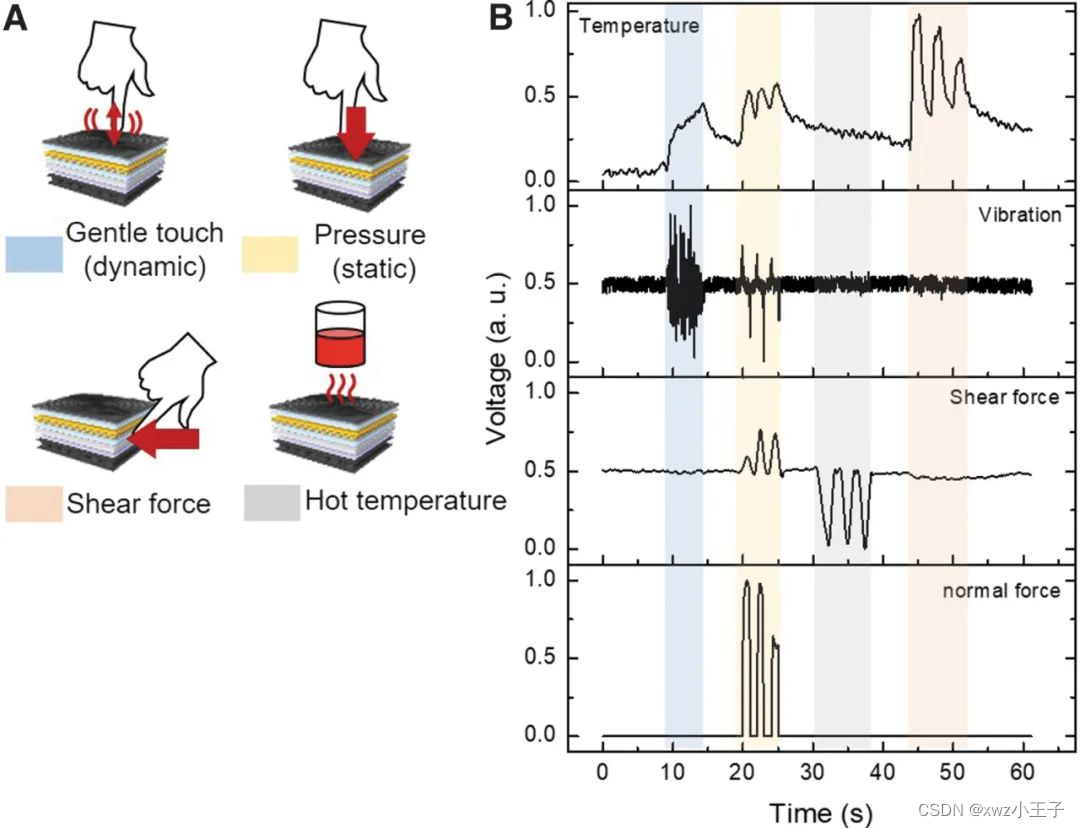
如何让机器人具备实时、多模态的触觉感知能力?
人类能够直观地感知和理解复杂的触觉信息,是因为分布在指尖皮肤的皮肤感受器同时接收到不同的触觉刺激,并将触觉信号立即传输到大脑。尽管许多研究小组试图模仿人类皮肤的结构和功能,但在一个系统内实现类似人类的触觉感知过程仍然是一个挑战…...

datax
DataX DataX 是阿里巴巴集团内被广泛使用的离线数据同步工具/平台,实现包括 MySQL、SQL Server、Oracle、PostgreSQL、HDFS、Hive、HBase、OTS、ODPS 等各种异构数据源之间高效的数据同步功能。 https://github.com/alibaba/DataX Features DataX本身作为数据同…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
