【数据不完整?用EM算法填补缺失】期望值最大化 EM 算法:睹始知终
期望值最大化算法 EM:睹始知终
- 算法思想
- 算法推导
- 算法流程
- E步骤:期望
- M步骤:最大化
- 陷入局部最优的原因
- 算法应用
- 高斯混合模型(Gaussian Mixture Model, GMM)
- 问题描述
- 输入输出
- Python代码实现
算法思想
期望值最大化方法,是宇宙演变、物种进化背后的动力。
如果一个公司在制定年终奖标准时,把每个员工一半的奖金和公司价值观挂钩,人们就会背诵创始人每个语录 — 整个公司都会自动迭代寻找最优解,每个人说话都是公司价值观。
如果一个国家足球不行,把每个孩子的高考分数和足球水平挂钩,人们就会大力投资足球设施,大爷大妈也会把广场让出去给孙子踢足球,谁跟我孙子抢我真的会发疯 — 整个国家都会自动迭代寻找最优解,每个人说话都是公司价值观。
这个思想在算法中就是期望最大化 EM 算法,只要给出一个收益函数, 计算机就会自动的寻找收益最大的那个点。
- 在每一时刻,算出能够最大化收益(期望值)的方向,沿着这个方向走一小步
- 然后再从新的起点重复这个过程,不论从何处起始,最后一定能够达到收益最大的那个终点
EM 算法本质是迭代策略,用于含有隐变量的统计模型中,交替计算期望步骤和最大化步骤,来寻找参数的最优估计。
比如看故事书,但故事中有一些缺失的部分(这些就是隐变量)。
你的目标是填补这些缺失部分,使得整个故事变得连贯和合理。
EM 算法就像一个两步循环过程,帮助你逐渐完善这个故事:
-
期望步骤 (E 步骤): 在这一步,你根据目前所知的信息,对故事中缺失的部分做出最佳猜测。就好比你根据故事的上下文来推测这些缺失部分可能的内容。
-
最大化步骤 (M 步骤): 接下来,你根据这些猜测来重新讲述整个故事,并调整故事中其他已知部分的细节,使得整体故事更加合理。这个过程就像根据新的假设来优化故事的连贯性。(M步骤可以使用 MLE 或 MAP)。
这个循环反复进行:你根据当前的故事版本来改善你对缺失部分的猜测,然后再用这些新猜测来优化整个故事。
随着每次迭代,故事变得越来越连贯,直到最终达到一个点,你觉得再怎么调整也无法使故事更好了。
这时,你就找到了最合适的版本来填补缺失部分,你找到了模型参数的最优估计。
再如 市场营销策略:
-
公司在设计营销策略时,通常会试图理解消费者的隐藏需求和偏好(隐藏变量),并据此调整其产品或服务(参数)。
-
通过市场反馈,公司不断调整其策略以最大化销售或品牌影响力,这类似于EM算法的期望步骤和最大化步骤的迭代过程。
算法推导
EM 算法论文:https://web.mit.edu/6.435/www/Dempster77.pdf
概率图模型再复杂都可以简化成俩个变量:观测变量x、隐变量z
比如你正在看一部电影:
- 电影中你能直接看到的场景和角色对话等就像是“观测变量”,这些是你直接获得的信息,不需要猜测或推理。
- 然而,电影也有许多你看不到的部分,比如角色的内心想法、未展示的背景故事,或者导演留下的悬念。这些就像是“隐变量”,你无法直接观察它们,但它们对整个故事的剧情发展(趋势就是人心所向)至关重要。
p ( x ∣ θ ) = ∏ i = 1 n p ( x i ∣ θ ) L ( θ ) = log p ( x ∣ θ ) = ∑ i = 1 n log p ( x i ∣ θ ) = ∑ i = 1 n log ∑ z p ( x i , z i ∣ θ ) \begin{aligned} &p(\mathbf{x}|\theta) \begin{aligned}=\prod_{i=1}^np(x_i|\theta)\end{aligned} \\ &{ L ( \theta )} =\operatorname{log}p(\mathbf{x}|\theta) \\ &=\sum_{i=1}^n\log p(x_i|\theta) \\ &=\sum_{i=1}^n\log\sum_zp(x_i,z_i|\theta) \end{aligned} p(x∣θ)=i=1∏np(xi∣θ)L(θ)=logp(x∣θ)=i=1∑nlogp(xi∣θ)=i=1∑nlogz∑p(xi,zi∣θ)
那我们逐步拆解公式原意:
-
联合概率分布:
- 第一行公式表示,观测数据集 x 在给定参数 θ 的条件下的联合概率分布
- 比如你有 3 张卡片,每张卡片上都有一个秘密数字,这个数字可以是 1、2、3 中的任何一个,我们现在要猜每张卡片上的数字是什么。每张卡片上数字的猜测都是独立的,不会影响其他卡片上的猜测。
- 在数学中,这就是我们说的“联合概率分布”,即我们想知道,所有卡片上每一种可能的数字组合出现的整体概率是多少。
- 如所有卡片上都是1的概率是多少(111)、如所有卡片上是123的概率是多少(123)、(222)、(321)、…、(333) 所有可能的数字组合及其相应的概率。
-
对数似然函数:
- 第二行公式,为了不忘记我们的猜测,我们决定把每次猜的结果写在一个日记本上。因为数字可能很大,所以我们用一种特别的数学“捷径”来记日记,这种捷径就是对数。这样,即使我们猜的数字很大,日记本上的数字也不会太长,更容易计算。
- 在数学中,写在日记本上的这种方法叫做“对数似然函数”,一个帮助我们处理大数字的数学工具。
-
对数似然的求和:
- 第三行公式,现在我们决定把日记本上所有的数字加起来,因为我们用了对数,所以加起来很容易。这就像是玩一个加法游戏,把所有的小数字加起来,得到一个总分。
-
边缘概率:
- 第四行公式,第1张是1、第2张是2,第 3 张卡片藏在盒子里(只有第 3 张未知),我们只知道盒子里可能藏着什么数字(1、2、3)。那先专注于部分已知信息,而忽略未知部分的具体细节,猜对所有看得见的卡片的概率是多少。
- 就是计算 第1张是1、第2张是2 的概率,忽略第三张卡片可能的值。
- 这就是数学中的“边缘概率” —— 它允许我们在部分信息未知的情况下,仍对已知部分进行概率计算。
在概率分布上,就是先猜一个 z 的分布(记为 q),使用 E、M 步骤,去逼近真实分布 L ( θ ) L(\theta) L(θ):

最后让猜的分布像爬楼梯一样,找到真实分布 L ( θ ) L(\theta) L(θ) 的最高点(最优解)。
用数学公式描述这个过程:
L ( θ ) = ∑ i = 1 n log ∑ z p ( x i , z i ∣ θ ) = ∑ i = 1 n log ∑ z ∞ q i ( z ) p ( x i , z i ∣ θ ) q i ( z ) ≥ ∑ i = 1 n ∑ z q i ( z ) log p ( x i , z i ∣ θ ) q i ( z ) \begin{aligned} L(\theta)& \begin{aligned}=&\sum_{i=1}^n\log\sum_zp(x_i,z_i|\theta)\end{aligned} \\ &\begin{aligned}=&\sum_{i=1}^n\log\sum_z^\infty q_i(z)\frac{p(x_i,z_i|\theta)}{q_i(z)}\end{aligned} \\ &\geq\sum_{i=1}^n\sum_zq_i(z)\log\frac{p(x_i,z_i|\theta)}{q_i(z)} \\ \end{aligned} L(θ)=i=1∑nlogz∑p(xi,zi∣θ)=i=1∑nlogz∑∞qi(z)qi(z)p(xi,zi∣θ)≥i=1∑nz∑qi(z)logqi(z)p(xi,zi∣θ)
-
第一行: L ( θ ) = ∑ i = 1 n log ∑ z p ( x i , z i ∣ θ ) L(\theta) = \sum_{i=1}^n \log \sum_z p(x_i, z_i|\theta) L(θ)=∑i=1nlog∑zp(xi,zi∣θ)
- 比如你正在玩一个寻宝游戏,你有一张地图( θ \theta θ),地图上标记了很多可能藏宝的地方(这里的藏宝地方就是 x i x_i xi 和 z i z_i zi)。
- x i x_i xi 是你可以看到的地方,而 z i z_i zi 是地图上标记的,但实际上可能藏宝也可能没藏宝的秘密地方。这一行的意思是,你在尝试弄清楚,根据地图,每个地方藏宝的可能性有多大。
-
第二行: = ∑ i = 1 n log ∑ z ∞ q i ( z ) p ( x i , z i ∣ θ ) q i ( z ) = \sum_{i=1}^n \log \sum_z^\infty q_i(z) \frac{p(x_i, z_i|\theta)}{q_i(z)} =∑i=1nlog∑z∞qi(z)qi(z)p(xi,zi∣θ)
- 这一步就像你在用一种特别的放大镜 q i ( z ) q_i(z) qi(z) 来看地图( θ \theta θ)。
- 这个放大镜可以告诉你,每个秘密地方真的藏宝的机会有多大。
- 你用这个放大镜和地图一起,来计算每个地方可能藏宝的几率。
-
第三行: ≥ ∑ i = 1 n ∑ z q i ( z ) log p ( x i , z i ∣ θ ) q i ( z ) \geq \sum_{i=1}^n \sum_z q_i(z) \log \frac{p(x_i, z_i|\theta)}{q_i(z)} ≥∑i=1n∑zqi(z)logqi(z)p(xi,zi∣θ)
- 最后,这一步就像你在记录你的发现。
- 对于地图上的每一个地方,你都写下了:根据我的放大镜和地图,我认为这里藏宝的机会有多大。”
- 这样,你就得到了一个完整的藏宝地图,上面标记了所有可能藏宝的地方和它们的可能性。
然后根据 Jeasen 不等式,得到公式的下界。
最终的公式是: J ( z , q ) J(z,q) J(z,q)。
- 不断的改变 z,就能不断搜索 θ \theta θ 最大值(概率分布图中的最高点)
于是,EM 算法可分为 E 步骤、M 步骤。
算法流程
E步骤:期望

E 步骤:猜的分布 q 不变,最大化 z。
在图中,q 沿着 x 轴上升,碰到真实分布z 就停止,开始 M 步骤。
M步骤:最大化

M 步骤:猜的分布 q 寻优,z 不变。
在图中,q 沿着 y 轴水平移动,碰不到真实分布z 就停止,开始 E 步骤。
陷入局部最优的原因
EM 算法可能会陷入局部最优。
-
非凸目标函数:EM算法通常用于优化非凸(non-convex)的目标函数。在非凸函数中,可能存在多个局部最优解,这意味着算法可能会在达到一个局部最优点后停止,而这个点不一定是全局最优的。
-
初始值依赖性:EM算法的结果往往依赖于初始参数的选择。如果初始参数选得不好,算法可能会被引导到一个局部最优解而不是全局最优解。
-
迭代方式:EM算法通过交替执行其两个步骤(E步和M步)来逐渐改进参数估计。这种迭代方式可能会导致算法“陷入”某个局部区域的最优解,特别是在目标函数有多个峰值的情况下。
-
模型复杂性和数据的局限性:在一些复杂模型或者数据不足的情况下,EM算法可能无法准确估计出全局最优参数,从而陷入局部最优。
解决这些问题的一种方法是通过多次运行算法,每次使用不同的初始参数,然后从中选择最好的结果。
此外,还可以使用全局优化技术,如模拟退火或遗传算法,来辅助找到更接近全局最优的解。
算法应用
高斯混合模型(Gaussian Mixture Model, GMM)
问题描述
假设我们有一组观测数据点,我们认为这些数据点是由两个不同的高斯分布生成的,但我们不知道每个数据点来自哪个高斯分布。
我们的目标是估计这两个高斯分布的参数(均值和方差)以及每个分布对应的混合系数。
输入输出
- 输入:一组观测数据点。
- 输出:两个高斯分布的参数(均值和方差)和混合系数。
Python代码实现
import numpy as np
from sklearn.mixture import GaussianMixture# 模拟数据生成
np.random.seed(0)
data = np.concatenate([np.random.normal(0, 1, 300), np.random.normal(5, 1.5, 700)]).reshape(-1, 1)# 应用EM算法
gmm = GaussianMixture(n_components=2, random_state=0)
gmm.fit(data)# 输出结果
print(f'均值: {gmm.means_.ravel()}')
print(f'方差: {gmm.covariances_.ravel()}')
print(f'混合系数: {gmm.weights_.ravel()}')
这段代码首先生成了一些模拟数据,数据是由两个不同的高斯分布合成的。
然后使用sklearn库中的GaussianMixture模型来应用EM算法。最后,打印出两个高斯分布的均值、方差以及混合系数。
相关文章:

【数据不完整?用EM算法填补缺失】期望值最大化 EM 算法:睹始知终
期望值最大化算法 EM:睹始知终 算法思想算法推导算法流程E步骤:期望M步骤:最大化陷入局部最优的原因 算法应用高斯混合模型(Gaussian Mixture Model, GMM)问题描述输入输出Python代码实现 算法思想 期望值最大化方法&a…...

PMP证书可以挂靠吗?
PMP证书不是国内的证书,挂靠不了呀,想挂靠,可以考软考/一建等,里面也有项目管理相关的证书。 PMP证书虽然不能挂靠,但是用处还是很大的,例如提升个人能力、薪资待遇,还有持证可享一些城市的福利…...

HTML语义化的理解
HTML语义化是指在编写HTML代码时,合理地选择适当的标签和属性来描述页面的结构和内容,使得代码更具有可读性、可维护性和可访问性。 可读性:通过使用语义化的标签,可以清晰地表达页面的结构和内容,使得代码更易于阅读和…...
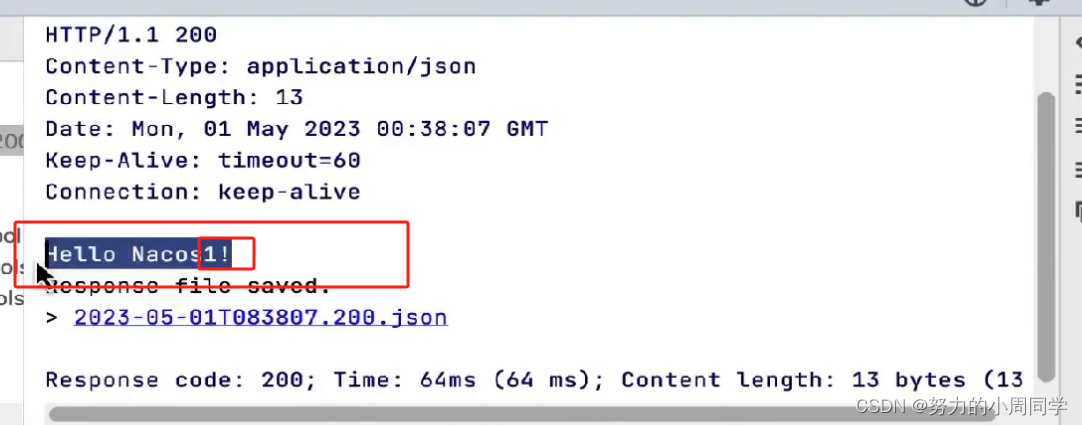
(Java企业 / 公司项目)注册,配置中心Nacos的怎么使用?(含相关面试题)(一)
在企业项目中使用Nacos实现的功能操作,以及如何在自己的环境中搭建Nacos环境,包含demo 一. 官网介绍:home (nacos.io) 文档地址:Nacos 快速开始 二. 准备Nacos环境 在公司里面很多的服务以及环境都是自己搭建的所以我在这里就从…...

计算机网络---知识点
ARPANET----NFSNET—ANSNET—Internet发展及协议 移动互联网 物联网 无线自组网、无线传感器网络、无线个域网 ISO/OSI网络体系结构 TCP/IP网络体系结构 对等通信、PDU 电路交换、报文交换、分组报文交换 虚电路、数据报 信道复用技术 网络性能的主要指标(…...

力扣42. 接雨水
双指针法 思路: 将数组前后设置为 left、right 指针,相互靠近;在逼近的过程中记录两端最大的值 leftMax、rightMax,作为容器的左右边界;更新指针规则: 如果数组左边的值比右边的小,则更新 left…...
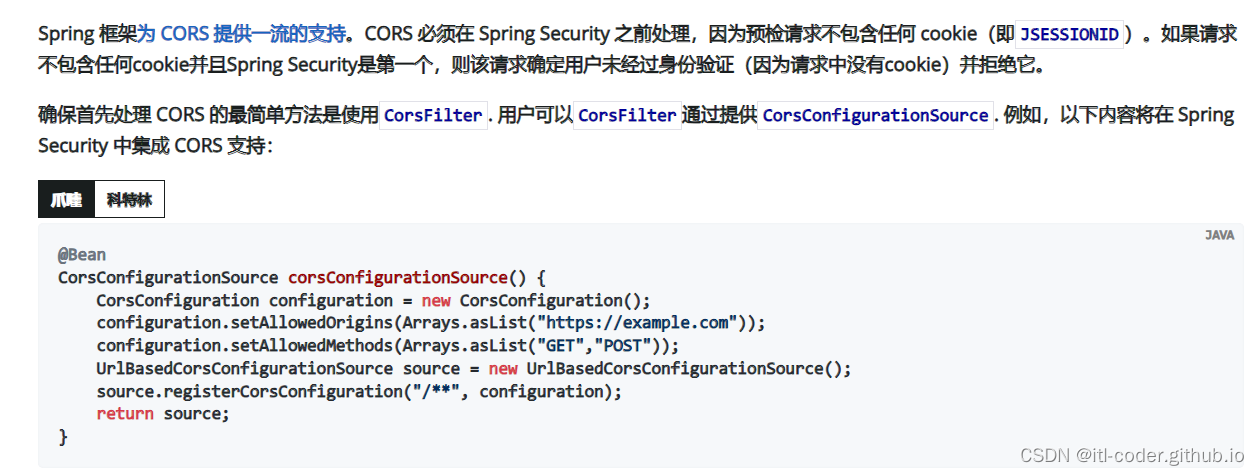
SpringSecurity-2.7中跨域问题
SpringSecurity-2.7中跨域问题 访问测试 起因 写这篇的起因是会了解到 SSM(CrosOrigin)解决跨域,但是会在加入SpringSecurity配置后,这个跨域解决方案就失效了,而/login这个请求上是无法添加这个注解或者通过配置(WebMvcConfig)去解决跨域,所以只能使用SpringSecurity提供的.c…...

Java解决字典序最小回文串
Java解决字典序最小回文串 01 题目 给你一个由 小写英文字母 组成的字符串 s ,你可以对其执行一些操作。在一步操作中,你可以用其他小写英文字母 替换 s 中的一个字符。 请你执行 尽可能少的操作 ,使 s 变成一个 回文串 。如果执行 最少 操…...

【力扣100】207.课程表
添加链接描述 class Solution:def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:# 思路是计算每一个课的入度,然后使用队列进行入度为0的元素的进出# 数组:下标是课程号,array[下标]是这个课程的入度# 哈希…...

2024年生成式AI支出将翻倍,到2027年将超1500亿美元
据国际数据公司(IDC)的预测,2023年全球企业在生成式人工智能(GenAI)解决方案上的投资已达194亿美元,预计在2024年将翻番。该预测还指出,包括GenAI软件、相关硬件和服务在内的支出将在2027年达到1511亿美元,…...

【代码随想录】刷题笔记Day42
前言 这两天机器狗终于搞定了,一个控制ROS大佬,一个计院编程大佬,竟然真把创新点这个弄出来了,牛牛牛牛(菜鸡我只能负责在旁边喊加油)。下午翘了自辩课来刷题,这次应该是元旦前最后一刷了&…...
数据库云平台新数科技完成B轮融资,打造全链路智能化数据库云平台
数据库云平台软件厂商「北京新数科技有限公司」(以下简称「新数科技」)已于2023年完成B1轮和B2轮融资,分别由渤海创富和彬复资本投资;义柏资本担任本轮融资独家财务顾问。 新数科技成立于2014年,当前产品矩阵包括数据库…...

【Linux 内核源码分析】Linux内核通知链机制
Linux内核通知链(notifier chain)是一种机制,用于实现内核中的事件通知和处理。它提供了一种灵活的方式,让不同的模块可以注册自己感兴趣的事件,并在事件发生时接收到通知。 通知链由一个或多个注册在其中的回调函数组…...

2023年度回顾:怿星科技的转型与创新
岁月不居,时节如流。随着2023年的落幕,怿星科技在这一年中不仅实现了自身的转型,还在技术创新、产品研发、行业合作和人才培养等方面取得了显著的成就。这一年,怿星科技正式完成了从服务型公司向产品型公司的战略转变,…...

STM32MP157D-DK1 Qt程序交叉编译与运行测试
上篇文章介绍了STM32MP157D-DK1开发板Qt镜像的构建,通过在Ubuntu中重新编译带有Qt功能的系统来实现。 本篇在上篇的基础上,继续搭建Qt的交叉编译环境,实现Qt程序在Ubuntu中编译,在STM32MP157板子中运行。 1 编译安装SDK 在上篇…...

Rancher 单节点 docker 部署备份与恢复
Rancher 单节点 docker 部署备份与恢复 1. 备份集群 获取 rancher server 容器名,本例为 angry_aryabhata docker ps | grep rancher/rancher6a27b8634c80 rancher/rancher:v2.5.14 xxx angry_aryabhata停止容器 docker stop angry_aryabhata创建备…...

WPF容器的背景对鼠标事件的影响
背景:在实现鼠标拖动窗口的过程中发现对父容器设置了鼠标拖动窗口的事件MouseLeftButtonDown private void DragWindow(object sender, MouseButtonEventArgs e) {if (e.LeftButton MouseButtonState.Pressed)DragMove(); } 问题:非常困惑的是&#x…...

pve虚拟机无法开机‘ha-manager set vm:101 --state started‘ failed: exit code 255
pve虚拟机无法开机,提示 ha-manager set vm:101 --state started failed: exit code 255 () Requesting HA start for VM 101 service vm:101 in error state, must be disabled and fixed first TASK ERROR: command ha-manager set vm:101 --state started fail…...

官宣!亚信安全TrustOne实力代言“中国新一代终端安全”
近日,IDC《中国新一代终端安全市场洞察,2023——安全防御的“最前线”》发布,正式定义了“中国新一代终端安全”的技术概念、技术演进和技术特点。该报告基于大量市场调研和数据分析,深入阐释了中国终端安全市场现状及面临的困局&…...

Text visualization : pipeline,wordle,phrase net,word tree
Text visualization(文本可视化)是一种将文本数据转换为可视形式的技术,以便更好地理解和分析文本内容。以下是可能会涉及的几个知识点: 1. Pipeline(流程图):Pipeline是指将文本可视化的过程划…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
