数据结构OJ实验11-拓扑排序与最短路径
A. DS图—图的最短路径(无框架)
题目描述
给出一个图的邻接矩阵,输入顶点v,用迪杰斯特拉算法求顶点v到其它顶点的最短路径。
输入
第一行输入t,表示有t个测试实例
第二行输入顶点数n和n个顶点信息
第三行起,每行输入邻接矩阵的一行,以此类推输入n行
第i个结点与其它结点如果相连则为距离,无连接则为0,数据之间用空格隔开。
第四行输入一个顶点v,表示求该顶点v到其他顶点的最短路径距离
以此类推输入下一个示例
输出
对每组测试数据,输出:
每行输出顶点v到某个顶点的最短距离和最短路径
每行格式:顶点v编号-其他顶点编号-最短路径值----[最短路径]。没有路径输出:顶点v编号-其他顶点编号--1。具体请参考示范数据
样例查看模式
正常显示查看格式
输入样例1
2\n
5 0 1 2 3 4\n
0 5 0 7 15\n
0 0 5 0 0\n
0 0 0 0 1\n
0 0 2 0 0\n
0 0 0 0 0\n
0\n
6 V0 V1 V2 V3 V4 V5\n
0 0 10 0 30 100\n
0 0 5 0 0 0\n
0 0 0 50 0 0\n
0 0 0 0 0 10\n
0 0 0 20 0 60\n
0 0 0 0 0 0\n
V0
输出样例1
0-1-5----[0 1 ]\n
0-2-9----[0 3 2 ]\n
0-3-7----[0 3 ]\n
0-4-10----[0 3 2 4 ]\n
V0-V1--1\n
V0-V2-10----[V0 V2 ]\n
V0-V3-50----[V0 V4 V3 ]\n
V0-V4-30----[V0 V4 ]\n
V0-V5-60----[V0 V4 V3 V5 ]\n
AC代码
#include<bits/stdc++.h>
using namespace std;
const int inf = 0x3f3f3f3f;
vector<vector<int>>a(5);
class Graph
{int n;vector<string>v;vector<vector<int>>adj;vector<string>path;vector<int>d;string start;
public:Graph(){cin >> n;path.resize(n);d.resize(n);for (int i = 0; i < n; i++){string x;cin >> x;v.push_back(x);}adj.resize(n);for (int i = 0; i < n; i++){adj[i].resize(n);}for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){cin >> adj[i][j];if (adj[i][j] == 0){adj[i][j] = inf;}}}cin >> start;}void shortpacth(){int sv, cur, mind;vector<bool>final;final.resize(n);for (int i = 0; i < n; i++){if (v[i] == start){sv = i;break;}}for (int i = 0; i < n; i++){path[i].append(start + " ");d[i] = inf;if (adj[sv][i] < inf){d[i] = adj[sv][i];path[i].append(v[i] + " ");}final[i] = 0;}d[sv] = 0;final[sv] = 1;for (int i = 0; i < n - 1; i++){mind = inf;for (int j = 0; j < n; j++){if (!final[j]){if (d[j] < mind){cur = j;mind = d[j];}}}final[cur] = 1;for (int j = 0; j < n; j++){if (!final[j] && (mind + adj[cur][j] < d[j])){d[j] = mind + adj[cur][j];path[j] = path[cur];path[j].append(v[j] + " ");}}}}void print(){for (int i = 0; i < n; i++){if (!d[i])continue;if (d[i] == inf)cout << start << "-" << v[i] << "--1" << endl;elsecout << start << "-" << v[i] << "-" << d[i] << "----[" << path[i] << "]" << endl;}}
};
int main()
{int t;cin >> t;while (t--){Graph g;g.shortpacth();g.print();}return 0;
}B. 图综合练习--拓扑排序
题目描述
已知有向图,顶点从0开始编号,求它的求拓扑有序序列。
拓扑排序算法:给出有向图邻接矩阵
1.逐列扫描矩阵,找出入度为0且编号最小的顶点v
2.输出v,并标识v已访问
3.把矩阵第v行全清0
重复上述步骤,直到所有顶点输出为止
--程序要求--
若使用C++只能include一个头文件iostream;若使用C语言只能include一个头文件stdio
程序中若include多过一个头文件,不看代码,作0分处理
不允许使用第三方对象或函数实现本题的要求
输入
第一行输入一个整数t,表示有t个有向图
第二行输入n,表示图有n个顶点
第三行起,输入n行整数,表示图对应的邻接矩阵
以此类推输入下一个图的顶点数和邻接矩阵
输出
每行输出一个图的拓扑有序序列
样例查看模式
正常显示查看格式
输入样例1
2\n
5\n
0 1 0 1 1\n
0 0 1 0 0\n
0 0 0 0 1\n
0 0 1 0 0\n
0 0 0 0 0\n
7\n
0 0 0 0 0 0 0\n
1 0 1 1 0 0 0\n
1 0 0 0 0 0 0\n
1 0 1 0 0 0 0\n
0 0 0 0 0 1 1\n
0 1 0 0 0 0 0\n
0 0 0 1 0 1 0\n
输出样例1
0 1 3 2 4 \n
4 6 5 1 3 2 0 \n
AC代码
#include<iostream>
using namespace std;
class graph
{int **adj;int n;
public:graph(){cin>>n;adj = new int* [n];for(int i=0;i<n;i++){adj[i]=new int [n]; for(int j=0;j<n;j++){cin>>adj[i][j];}}}~graph(){for(int i=0;i<n;i++){delete[]adj[i];}delete[]adj;}bool check(int x)//入度为0{for(int i=0;i<n;i++){if(adj[i][x])return 0;}return 1;}void torpot(){bool *visit;visit = new bool[n]{0};//为0int res=n;while(res--){for(int i=0;i<n;i++){if(!visit[i]&&check(i)){cout<<i<<" ";visit[i]=1;//更新for(int j=0;j<n;j++){adj[i][j]=0;}break;}}}cout<<endl;delete[]visit;}
};
int main()
{int t;cin>>t;while(t--){graph g;g.torpot();}return 0;
}C. 货币套汇(图路径)
题目描述
套汇是指利用货币汇兑率的差异将一个单位的某种货币转换为大于一个单位的同种货币。例如,假定1 美元可以买0.7 英镑,1 英镑可以买9.5 法郎,1法郎可以买到0.16美元。通过货币兑换,一个商人可以从1 美元开始买入,得到0.7×9.5×0.16=1.064美元,从而获得6.4%的利润。 给定n种货币c1 ,c2 ,... ,cn的有关兑换率,试设计一个有效算法,确定货币间是否存在套汇的可能性。
提示:判断图上是否出现正环,即环上所有的边相乘大于1
输入
第一行:测试数据组数
每组测试数据格式为:
第一行:正整数n (1< =n< =30),正整数m,分别表示n种货币和m种不同的货币兑换率。
2~n+1行,n种货币的名称。
n+2~n+m+1行,每行有3 个数据项ci,rij 和cj ,表示货币ci 和cj的兑换率为 rij。
输出
对每组测试数据,如果存在套汇的可能则输出YES
如果不存在套汇的可能,则输出NO。
样例查看模式
正常显示查看格式
输入样例1
2\n
3 3\n
USDollar\n
BritishPound\n
FrenchFranc\n
USDollar 0.5 BritishPound\n
BritishPound 10.0 FrenchFranc\n
FrenchFranc 0.21 USDollar\n
3 6\n
USDollar\n
BritishPound\n
FrenchFranc\n
USDollar 0.5 BritishPound\n
USDollar 4.9 FrenchFranc\n
BritishPound 10.0 FrenchFranc\n
BritishPound 1.99 USDollar\n
FrenchFranc 0.09 BritishPound\n
FrenchFranc 0.19 USDollar
输出样例1
YES\n
NO
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=50;
map<string,int>mp;
double a[N][N];
int n,m;
void floy()
{for(int k=0;k<n;k++){for(int i=0;i<n;i++){for(int j=0;j<n;j++){a[i][j]=max(a[i][j],a[i][k]*a[k][j]);}}}//判断是否存在正环for(int i=0;i<n;i++){if(a[i][i]>1){cout<<"YES"<<endl;return;}}cout<<"NO"<<endl;
}
int main()
{int t;cin>>t;while(t--){memset(a,0,sizeof(a));cin>>n>>m;for(int i=0;i<n;i++){string x;cin>>x;mp[x]=i;a[i][i]=1;//本身自己与自己的环}for(int i=0;i<m;i++){string s1,s2;double c;cin>>s1>>c>>s2;a[mp[s1]][mp[s2]]=c;}floy();}return 0;
}D. 关键路径-STL版
题目描述
给定有向图无环的边信息,求每个顶点的最早开始时间、最迟开始时间。
// 参考代码
#include <iostream>
#include <vector>
#include <string>
#include <queue>
using namespace std;class Vertex {
public:int indexNo;bool hasEnterQueue;int early;int later;Vertex(int indexNo) {this->indexNo = indexNo;this->hasEnterQueue = false;early = -1;later = 0x7FFFF;}void updateEarly(int parentEarly, int edgeValue) {int newEarly = parentEarly + edgeValue;if (newEarly > this->early)this->early = newEarly;}void updateLater(int childLater, int edgeValue) {int newLater = childLater - edgeValue;if (newLater < this->later)this->later = newLater;}
};class Graph {
public:vector<Vertex> vertexes;vector<vector<int> > adjMat;int n;
public:void readVertexes() {//TODO: 将顶点数读入成员变量n//TODO: 从输入初始化vertexes数组int i=0;for(; i<n; ++i) {Vertex v(i);this->vertexes.push_back(v);}//为成员变量adjMat创建内存,赋初值for(i=0; i<n; ++i) {vector<int> row;int j=0;for(; j<n; ++j) {//TODO: 将0增加到row最后}//TODO: 将row增加到adjMat最后}}void readAdjMatrix() {//read the adjacent info into this->adjMatint edges;cin >> edges;int i=0;int s, t, w; //s源顶点编号,t目的顶点编号,w边长for(; i<edges; ++i) {//TODO: 读入s,t,w,并将adjMat的第s行、第t列的值改为w.}}void updateEarly(int parentNo, queue<int>& earlyQue) {int parentEarly = vertexes[parentNo].early; //读入父结点early值int j=0;for(; j<n; ++j) {int edgeValue = adjMat[parentNo][j];if (edgeValue == 0) continue; //若父结点与结点j没有边相连,passVertex& child = vertexes[j];child.updateEarly(parentEarly, edgeValue); //更新子结点j的early信息if(!child.hasEnterQueue) {child.hasEnterQueue = true; //将子结点加入队列earlyQue.push(j);}}}void updateLater(int childNo, queue<int>& laterQue) {//TODO:}int getRoot() {//获取入度为0的顶点int j=0;for(; j<n; ++j) {int i=0;for(; i<n && adjMat[i][j] == 0; ++i);if (i>=n) return j; //j has not any in-edges.}return -1; //表示没找到}int getLeaf() {//TODO: 获取出度为0的顶点}void printEarlyLater(bool isEarly) {int i=0;for(; i<n; ++i) {Vertex& v = vertexes[i];if (isEarly)cout << v.early << " ";else {cout << v.later << " ";}}cout << endl;}void findEarly() {//执行关键路径算法,求每个顶点的最早开始时间。int r = getRoot();Vertex& root = vertexes[r];root.hasEnterQueue = true;root.early = 0;queue<int> que;que.push(r);while(!que.empty()) {int p = que.front();que.pop();updateEarly(p, que);}printEarlyLater(true);}void clearEnterQueue() {int i=0;for(; i<n; ++i) {vertexes[i].hasEnterQueue = false;}}void findLater() {//TODO:调用clearEnterQueue,以清除每个顶点的hasEnterQueue=false//执行关键路径算法,求每个顶点的最迟开始时间。}void main() {readVertexes();readAdjMatrix();findEarly();findLater();}
};int main() {int t=1;//cin >> t;while (t--) {Graph g;g.main();}return 0;
}输入
第一行图的顶点总数
第二行边的总数
第三行开始,每条边的时间长度,格式为源结点 目的结点 长度
输出
第一行:第个顶点的最早开始时间
第二行:每个顶点的最迟开始时间
样例查看模式
正常显示查看格式
输入样例1
9\n
12\n
0 1 3\n
0 2 10\n
1 3 9\n
1 4 13\n
2 4 12\n
2 5 7\n
3 6 8\n
3 7 4\n
4 7 6\n
5 7 11\n
6 8 2\n
7 8 5
输出样例1
0 3 10 12 22 17 20 28 33 \n
0 9 10 23 22 17 31 28 33
AC代码
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
const int N = 100000;
int n, m;
int in[N], early[N], later[N], top[N];
vector<int>edge[N];//邻接表
vector<int>value[N];//记录权值
int cnt;
void topsort()
{queue<int>q;for (int i = 0; i < n; i++){if (in[i] == 0)q.push(i);//入度为0}while (!q.empty()){int cur = q.front();q.pop();top[++cnt] = cur;//断开相邻边for (int i = 0; i < edge[cur].size(); i++){int j = edge[cur][i];--in[j];if (in[j] == 0){q.push(j);}}}
}
//只有按照拓扑序才能保证顶点的最晚和最早发生时间
void calEarlylater()
{//枚举拓扑序for (int i = 1; i <= cnt; i++){int tt = top[i];for (int j = 0; j < edge[tt].size(); j++){int ee = edge[tt][j], w = value[tt][j];early[ee] = max(early[ee], early[tt] + w);//终点的最早发生时间(与起点最早发生时间+dur)取最大值}}for (int i = 0; i < n; i++){cout << early[i] << " ";later[i] = early[top[cnt]];//每个顶点的最晚发生时间初始为拓扑序列最后一个顶点的最早发生时间}cout << endl;//拓扑序逆着求最晚发生时间for (int i = cnt; i >= 1; i--){int tt = top[i];for (int j = 0; j < edge[tt].size(); j++){int ee = edge[tt][j], w = value[tt][j];later[tt] = min(later[tt], later[ee] - w);//最晚发生时间求最小值//(大家都想晚点开始早点结束)}}for (int i = 0; i < n; i++){cout << later[i] << " ";}cout << endl;
}
int main()
{cin >> n >> m;while (m--){int s, t, w;cin >> s >> t >> w;edge[s].push_back(t);in[t]++;value[s].push_back(w);}topsort();calEarlylater();return 0;
}E. 旅游规划
题目描述
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
输入
输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是高速公路的条数;S是出发地的城市编号;D是目的地的城市编号。随后的M行中,每行给出一条高速公路的信息,分别是:城市1、城市2、高速公路长度、收费额,中间用空格分开,数字均为整数且不超过500。输入保证解的存在。
输出
在一行里输出路径的长度和收费总额,数字间以空格分隔,输出结尾不能有多余空格。
样例查看模式
正常显示查看格式
输入样例1
4 5 0 3\n
0 1 1 20\n
1 3 2 30\n
0 3 4 10\n
0 2 2 20\n
2 3 1 20
输出样例1
3 40
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=550;
pair<int,int> a[N][N];
int n,m,s,d;
void floyd()
{for(int k=0;k<n;k++){for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(a[i][j].first>a[i][k].first+a[k][j].first){a[i][j].first=a[i][k].first+a[k][j].first;a[i][j].second=a[i][k].second+a[k][j].second;}else if(a[i][j].first==a[i][k].first+a[k][j].first){if(a[i][j].second>a[i][k].second+a[k][j].second){a[i][j].second=a[i][k].second+a[k][j].second;a[i][j].first=a[i][k].first+a[k][j].first;}}}}}
}
int main()
{cin>>n>>m>>s>>d;//找s到d的最短路径for(int i=0;i<n;i++){for(int j=0;j<m;j++){a[i][j].first=a[j][i].first=a[i][j].second=a[j][i].second=0x3f3f3f3f;//非常重要!!}}for(int i=0;i<m;i++){int u,v,w,p;cin>>u>>v>>w>>p;a[u][v].first=a[v][u].first=w;a[v][u].second=a[u][v].second=p;}floyd();cout<<a[s][d].first<<" "<<a[s][d].second<<endl;return 0;
}F. 拯救007
题目描述
在老电影“007之生死关头”(Live and Let Die)中有一个情节,007被毒贩抓到一个鳄鱼池中心的小岛上,他用了一种极为大胆的方法逃脱 —— 直接踩着池子里一系列鳄鱼的大脑袋跳上岸去!(据说当年替身演员被最后一条鳄鱼咬住了脚,幸好穿的是特别加厚的靴子才逃过一劫。)
设鳄鱼池是长宽为100米的方形,中心坐标为 (0, 0),且东北角坐标为 (50, 50)。池心岛是以 (0, 0) 为圆心、直径15米的圆。给定池中分布的鳄鱼的坐标、以及007一次能跳跃的最大距离,你需要告诉他是否有可能逃出生天。
输入
首先第一行给出两个正整数:鳄鱼数量 N(≤100)和007一次能跳跃的最大距离 D。随后 N 行,每行给出一条鳄鱼的 (x,y) 坐标。注意:不会有两条鳄鱼待在同一个点上。
输出
如果007有可能逃脱,就在一行中输出"Yes",否则输出"No"。
样例查看模式
正常显示查看格式
输入样例1
14 20\n
25 -15\n
-25 28\n
8 49\n
29 15\n
-35 -2\n
5 28\n
27 -29\n
-8 -28\n
-20 -35\n
-25 -20\n
-13 29\n
-30 15\n
-35 40\n
12 12
输出样例1
Yes
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=110;
int g[N][N];
int pd[N];
int x[N],y[N];
int k,n;
bool check(int n,int m,int x1,int y1,int x2,int y2)
{if((sqrt(x1*x1+y1*y1)-15<=k))g[0][n]=1;//okif((sqrt(x2*x2+y2*y2)-15<=k))g[0][m]=1;//okif((50-abs(x1)<=k)||(50-abs(y1)<=k))pd[n]=1;if((50-abs(x2)<=k)||(50-abs(y2)<=k))pd[m]=1;return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)<=k*k;
}
bool flag=0;
void dfs(int n,int x)
{if(pd[x]==1)flag=1;for(int i=1;i<=n;i++){if(g[x][i]==1){g[x][i]=0;//跳完不再跳dfs(n,i);}}
}
int main()
{cin>>n>>k;for(int i=1;i<=n;i++){cin>>x[i]>>y[i];}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){//可以跳的地方先统计g[i][j]=g[j][i]=check(i,j,x[i],y[i],x[j],y[j]);}}dfs(n,0);if(flag||(double)k>=(1.0*50*sqrt(2)-7.5))cout<<"Yes"<<endl;else{cout<<"No"<<endl;}return 0;
}相关文章:

数据结构OJ实验11-拓扑排序与最短路径
A. DS图—图的最短路径(无框架) 题目描述 给出一个图的邻接矩阵,输入顶点v,用迪杰斯特拉算法求顶点v到其它顶点的最短路径。 输入 第一行输入t,表示有t个测试实例 第二行输入顶点数n和n个顶点信息 第三行起&…...

你的第一个JavaScript程序
JavaScript,即JS,JavaScript是一种具有函数优先的轻量级,解释型或即时编译型的编程语言。虽然它是作为开发Web页面的脚本语言而出名,但是它也被用到了很多非浏览器环境中,JavaScript基于原型编程、多范式的动态脚本语言…...
)
CMake入门教程【基础篇】列表操作(list)
文章目录 1. 定义列表2. 获取列表长度3. 获取列表元素4. 追加元素到列表末尾5. 插入元素到指定位置6. 移除指定位置的元素7. 移除指定值的元素8. 替换指定位置的元素9. 迭代列表元素 #mermaid-svg-IAjFPWI6IXEGYmuU {font-family:"trebuchet ms",verdana,arial,sans-…...

普中STM32-PZ6806L开发板(HAL库函数实现-读取内部温度)
简介 主芯片STM32F103ZET6,读取内部温度其他知识 内部温度所在ADC通道 温度计算公式 V25跟Avg_Slope值 参考文档 stm32f103ze.pdf 电压计算公式 Vout Vref * (D / 2^n) 其中Vref代表参考电压, n为ADC的位数, D为ADC输入的数字信号。 实现…...
普中STM32-PZ6806L开发板(使用过程中的问题收集)
Keil使用ST-Link 报错 Internal command error 描述: 在某一次使用过程中,前面都是正常使用, Keil在烧录时报错Internal command error, 试了网上的诸多方式, 例如 升级固件;ST-Link Utility 清除;Keil升级到最新版本;甚至笔者板子的Micro头也换了,因为坏…...
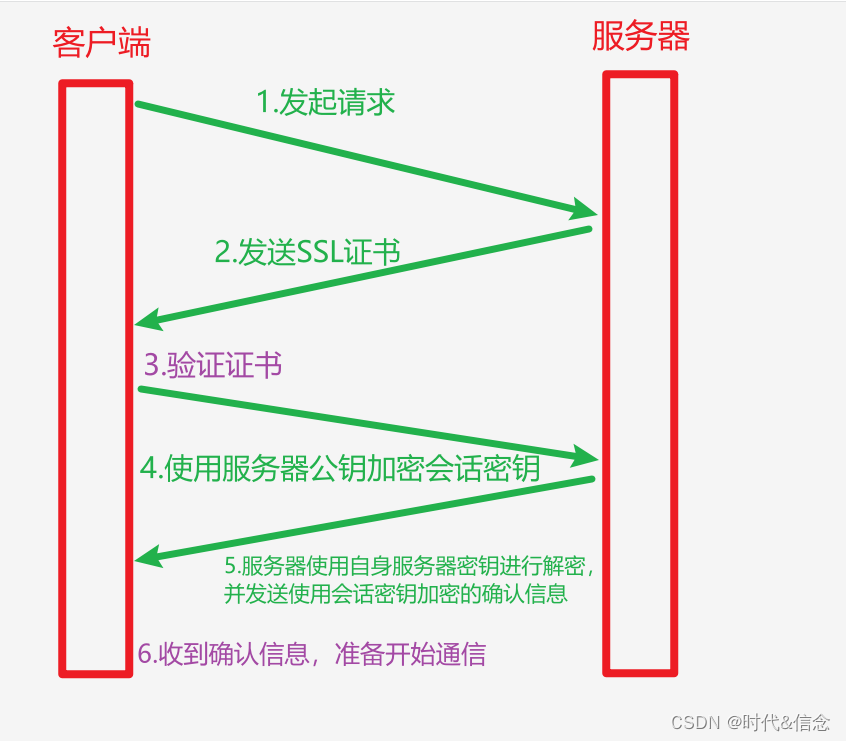
八股文打卡day12——计算机网络(12)
面试题:HTTPS的工作原理?HTTPS是怎么建立连接的? 我的回答: 1.客户端向服务器发起请求,请求建立连接。 2.服务器收到请求之后,向客户端发送其SSL证书,这个证书包含服务器的公钥和一些其他信息…...
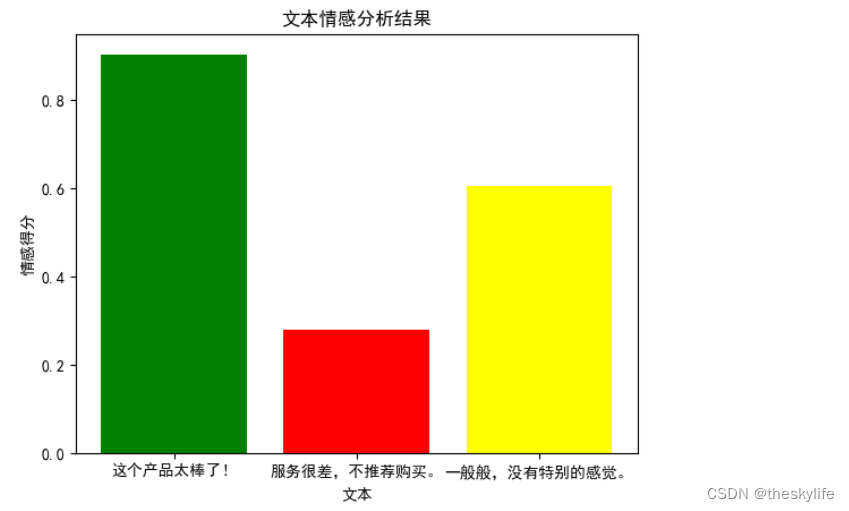
自然语言处理2——轻松入门情感分析 - Python实战指南
目录 写在开头1.了解情感分析的概念及其在实际应用中的重要性1.1 情感分析的核心概念1.1.1 情感极性1.1.2 词汇和上下文1.1.3 情感强度1.2 实际应用中的重要性 2. 使用情感分析库进行简单的情感分析2.1 TextBlob库的基本使用和优势2.1.1 安装TextBlob库2.1.2 文本情感分析示例2…...
pygame学习(一)——pygame库的导包、初始化、窗口的设置、打印文字
导语 pygame是一个跨平台Python库(pygame news),专门用来开发游戏。pygame主要为开发、设计2D电子游戏而生,提供图像模块(image)、声音模块(mixer)、输入/输出(鼠标、键盘、显示屏)…...

前端面试
1. 什么是MVVM,MVC,MVP模型? 软件架构模式: MVC: M: 模型,拉取数据的类。 V: 视图,展现给用户的视觉效果。 C: 控制器,通知M拉取数据,并且给V。 > MV…...
Spring Boot快速搭建一个简易商城项目【完成登录功能且优化】
完成登录且优化: 未优化做简单的判断: 全部异常抓捕 优化:返回的是json的格式 BusinessException:所有的错误放到这个容器中,全局异常从这个类中调用 BusinessException: package com.lya.lyaspshop.exce…...
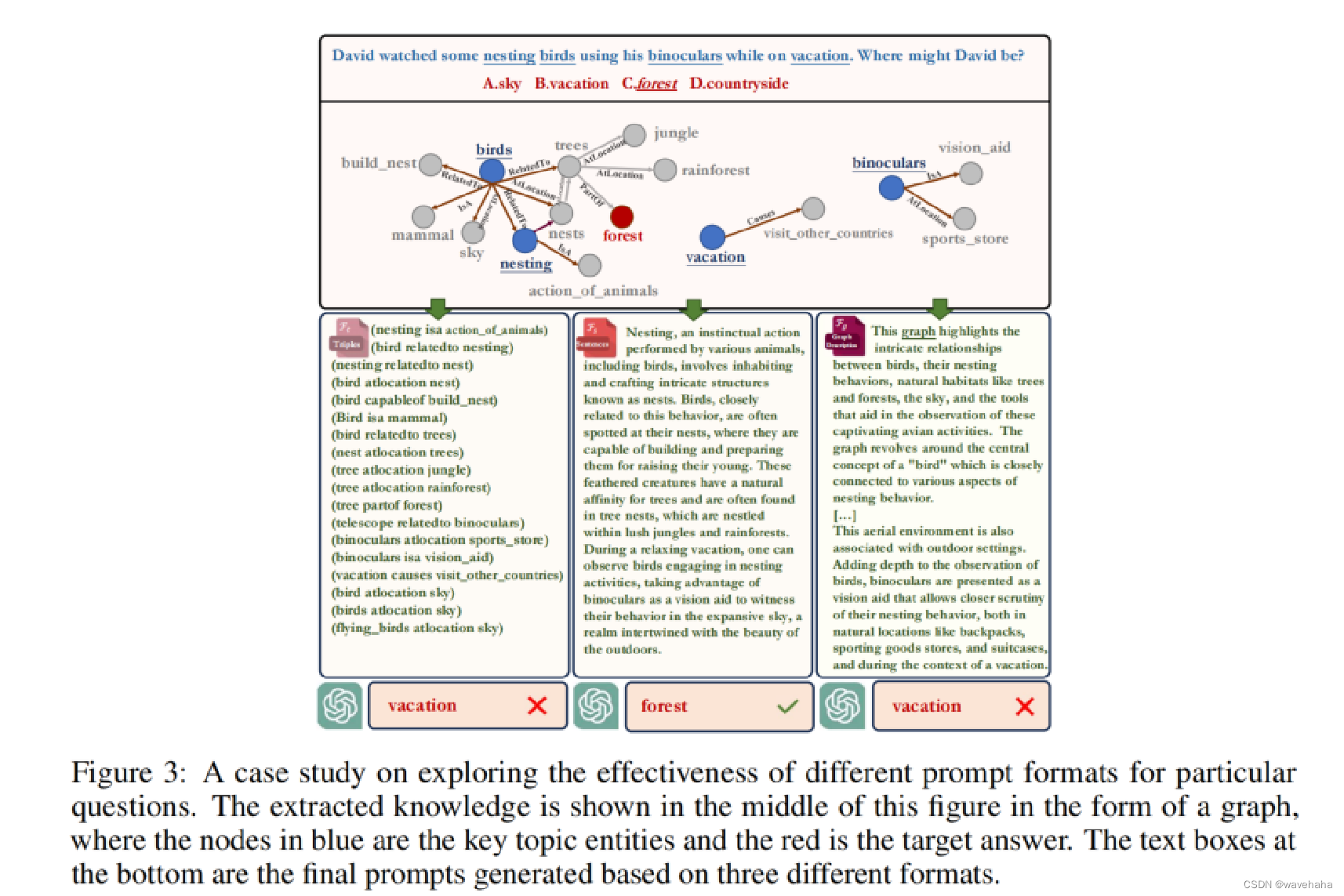
KG+LLM(一)KnowGPT: Black-Box Knowledge Injection for Large Language Models
论文链接:2023.12-https://arxiv.org/pdf/2312.06185.pdf 1.Background & Motivation 目前生成式的语言模型,如ChatGPT等在通用领域获得了巨大的成功,但在专业领域,由于缺乏相关事实性知识,LLM往往会产生不准确的…...
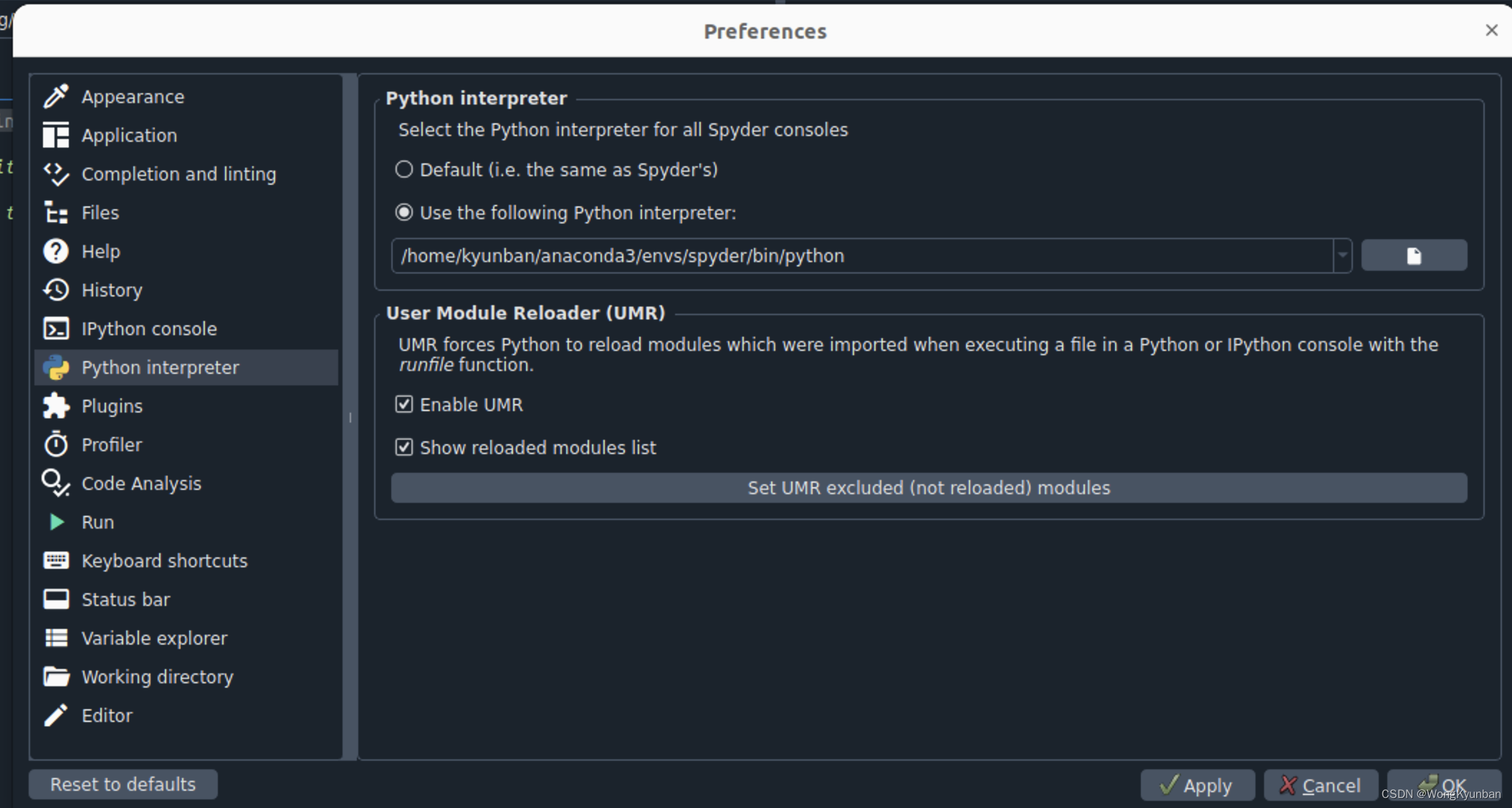
使用anaconda创建爬虫spyder工程
1.由于每个工程使用的环境都可能不一样,因此一个好的习惯就是不同的工程都创建属于自己的环境,在anaconda中默认的环境是base,我们现在来创建一个名为spyder的环境,专门用于爬虫工程: //括号中名字,代表当…...
-TCP协议解析)
网络通信(7)-TCP协议解析
目录 一、定义 二、主要特点 三、报文格式 四、工作方式...
win32 WM_MENUSELECT消息学习
之前写了一些win32的程序,处理菜单单击都是处理WM_COMMAND消息,通过 LOWORD(wParam) 获取菜单ID,判断单击的是哪个菜单项; 还有一些其他菜单消息; 当在菜单项中移动光标或鼠标,程序会收到许多WM_MENUSELEC…...
Java学习苦旅(十六)——List
本篇博客将详细讲解Java中的List。 文章目录 预备知识——初识泛型泛型的引入泛型小结 预备知识——包装类基本数据类型和包装类直接对应关系装包与拆包 ArrayList简介ArrayList使用ArrayList的构造ArrayList常见操作ArrayList遍历 结尾 预备知识——初识泛型 泛型的引入 我…...
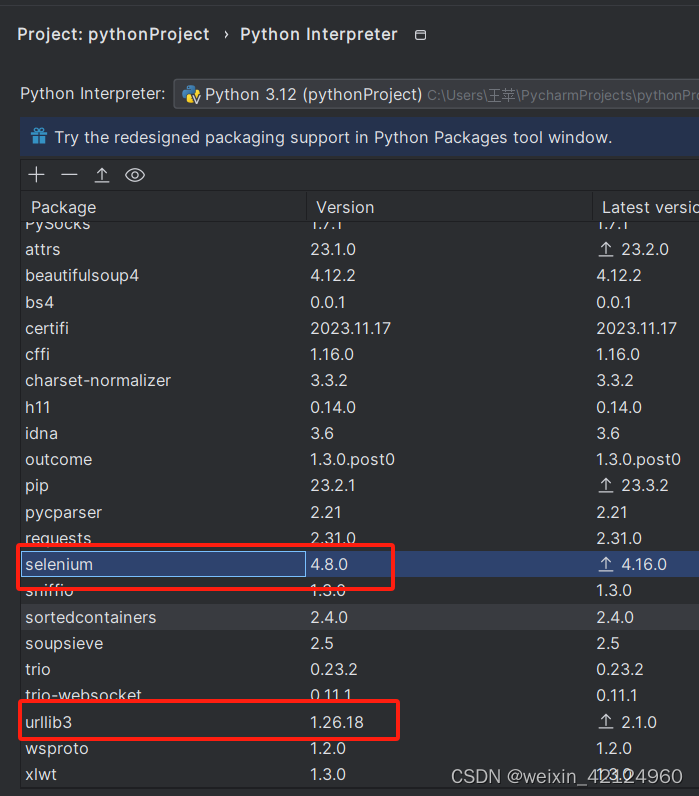
python爬虫实现获取招聘信息
使用的python版本: 3.12.1 selenium版本:4.8.0 urllib版本:1.26.18 from selenium import webdriver from selenium.webdriver import ActionChains import timeimport re import xlwt import urllib.parsedef get_html(url):chrome_drive…...
模块电源(七):LDO 应用
1、Typical application circuit LDO 典型应用电路如下图所示: 2、High Output Current Positive Voltage Regulator 通过 PNP 型三极管 Tr1 ,可以提高 LDO 的输出电流能力,电路如下图所示: 设流过 R1 的电流为 ,当 …...
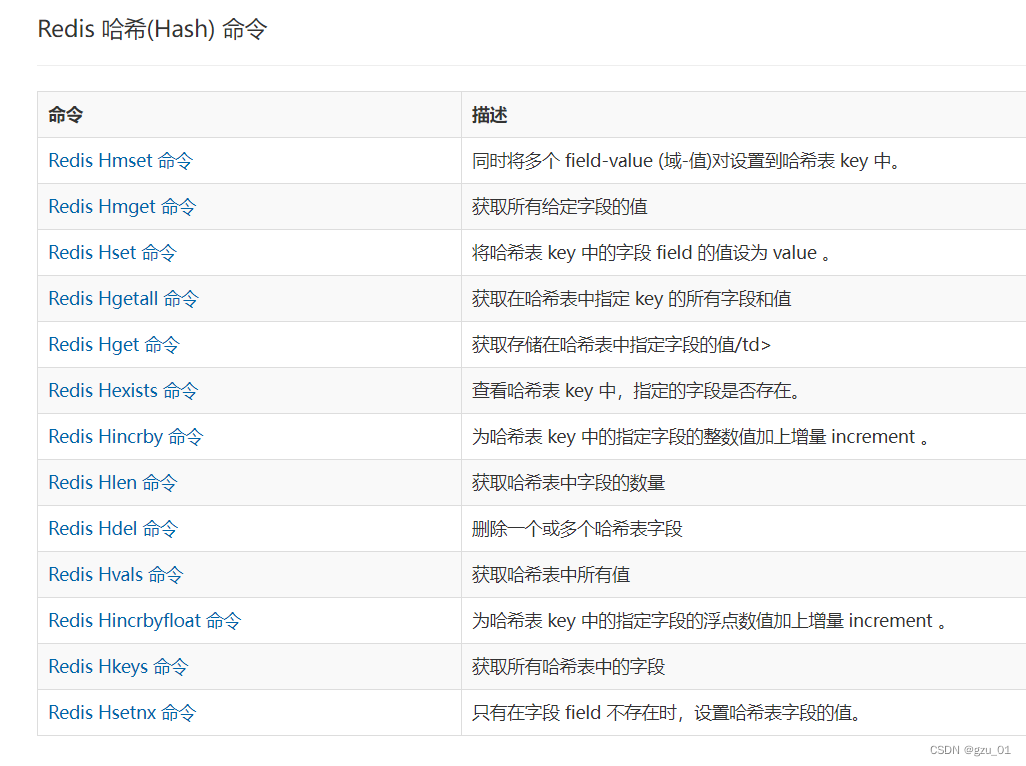
Redis命令---Hash(哈希)篇 (超全)
目录 1.Redis Hmset 命令 - 同时将多个 field-value (域-值)对设置到哈希表 key 中。简介语法可用版本: > 2.0.0返回值: 如果命令执行成功,返回 OK 。 示例 2.Redis Hmget 命令 - 获取所有给定字段的值简介语法可用版本: > 2.0.0返回值: 一个包含多个给定字段…...
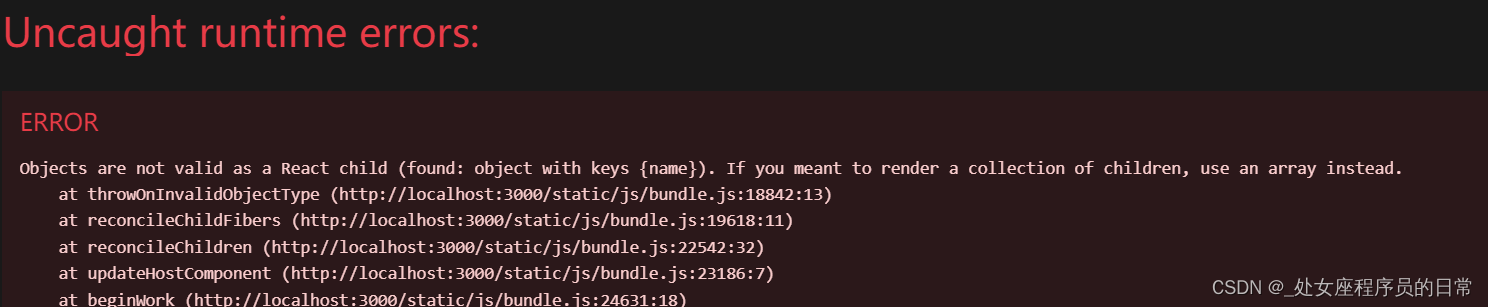
Objects are not valid as a React child (found: object with keys {name}).
在jsx中可以嵌套表达式,将表达式作为内容的一部分,但是要注意,普通对象不能作为子元素;但是数组,react元素对象是可以的 如下:不能将stu这个对象作为子元素放 function App() {const myCal imgStyleconst…...
nodejs业务分层如何写后端接口
这里展示的是在node express 项目中的操作 ,数据库使用的是MongoDB,前期关于express和MongoDB的文章可访问: Nodejs后端express框架 server后端接口操作:通过路由匹配——>调用对应的 Controller——>进行 Service调用——&…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
