【c语言】二叉树
主页:114514的代码大冒险
qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ )
Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com
引入
我们之前已经学过线性数据结构,今天我们将介绍非线性数据结构----树
望文生义,这个数据结构肯定与现实中的树, 有着一定的联系,如图:
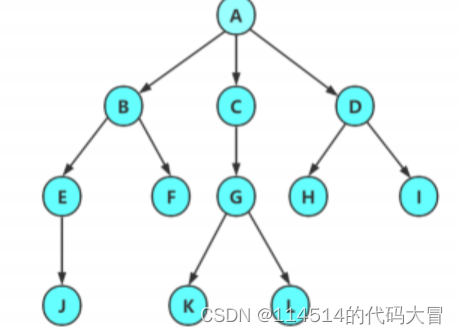

数据结构中的树它看起来像树枝,也想树的根部
树的概念

树的相关概念
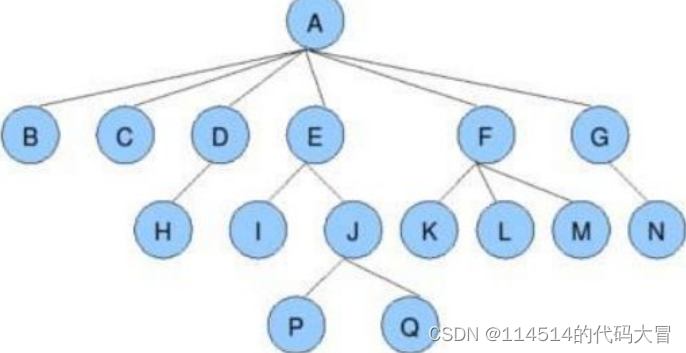
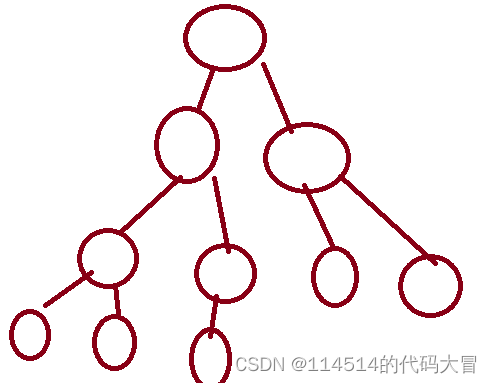
节点的度:一个节点含有的子树的个数称为该节点的度;如上图:A的为6叶节点或终端节点:度为0的节点称为叶节点;如上图:B、C、H、I...等节点为叶节点非终端节点或分支节点:度不为0的节点;如上图:D、E、F、G...等节点为分支节点双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;如上图:A是B的父节点孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;如上图:B是A的孩子节点兄弟节点:具有相同父节点的节点互称为兄弟节点;如上图:B、C是兄弟节点树的度:一棵树中,最大的节点的度称为树的度;如上图:树的度为6节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;树的高度或深度:树中节点的最大层次;如上图:树的高度为4堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙森林:由m(m>0)棵互不相交的树的集合称为森林;
树的表示
概念图:

树在实际中的运用(表示文件系统的目录树结构)
文件目录:

公司内部功能安排
二叉树(特殊的树)
这些都不重要
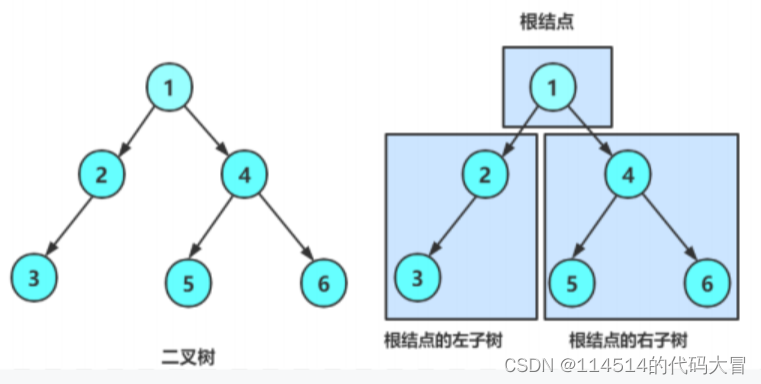
你只需要知道二叉树的每个节点最多两个孩子
可以没有孩子,也可以只有一个孩子
另外在二叉树中
左孩子和右孩子是有差异的
现实中的二叉树


1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^k-1,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。
说人话:
就是说如果除了最底下那一排(所谓的叶子节点)其他的节点都有两个孩子
我们就称之为满二叉树

那么什么是完全二叉树呢
就是除了树的倒数第二排之外,其他节点都有两个孩子
如图: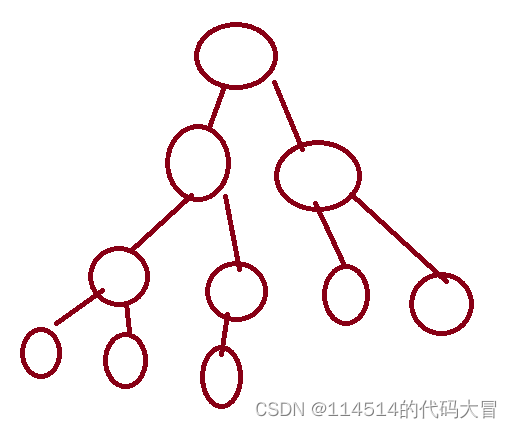
二叉树的性质


说了一大堆,能看懂多少算多少
我来说几个比较可能用到的点
 只要是树,有两个孩子的节点始终比没有孩子的节点的数量少一
只要是树,有两个孩子的节点始终比没有孩子的节点的数量少一
完全二叉树的坐标规律如右图所示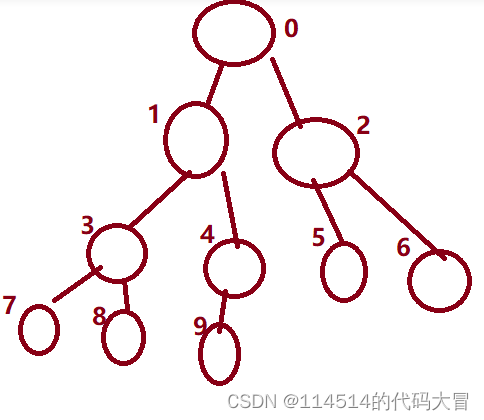
(完全二叉树中) 我们假使某节点这个下标为i,那么它的父亲就是
(i-1)/2 ,左孩子(如果有的话)为2*i+1,右孩子为左孩子坐标加1
另外还有就是这个完全二叉树的层数问题
除开最后一层外,第一层节点的数量为2^0,第二次为2^1第三次为2^2
第n层为2^(n-1),
如此满二叉树的节点数量为2^n - 1个
hhh,非满二叉树的节点数量则为前n-1层的节点数量+最后一层的节点数
我想,这个时候,在知道二叉树的节点的数量前提下
求出二叉树的深度,也就是层数不是什么困难的事情了
总结
这就是今天的树的概念讲解
这部分内容不需要太过焦虑
这些概念现在只是稍微有个大概就可以
我们在接下来的学习中会反复提到
相关文章:

【c语言】二叉树
主页:114514的代码大冒险 qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ ) Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com 引入 我们之前已经学过线性数据结构,今天我们将介绍非线性数据结构----树 树是一种非线性的…...
六、Java框架之SpringBoot
黑马课程 文章目录1. SpringBoot入门1.1 SpringBoot入门案例步骤1:创建SpringBoot项目高版本springboot常见错误步骤2:创建BookController步骤3:启动服务器并运行程序pom.xml示例1.2 官网创建SpringBoot1.3 SpringBoot工程快速启动问题导入打…...
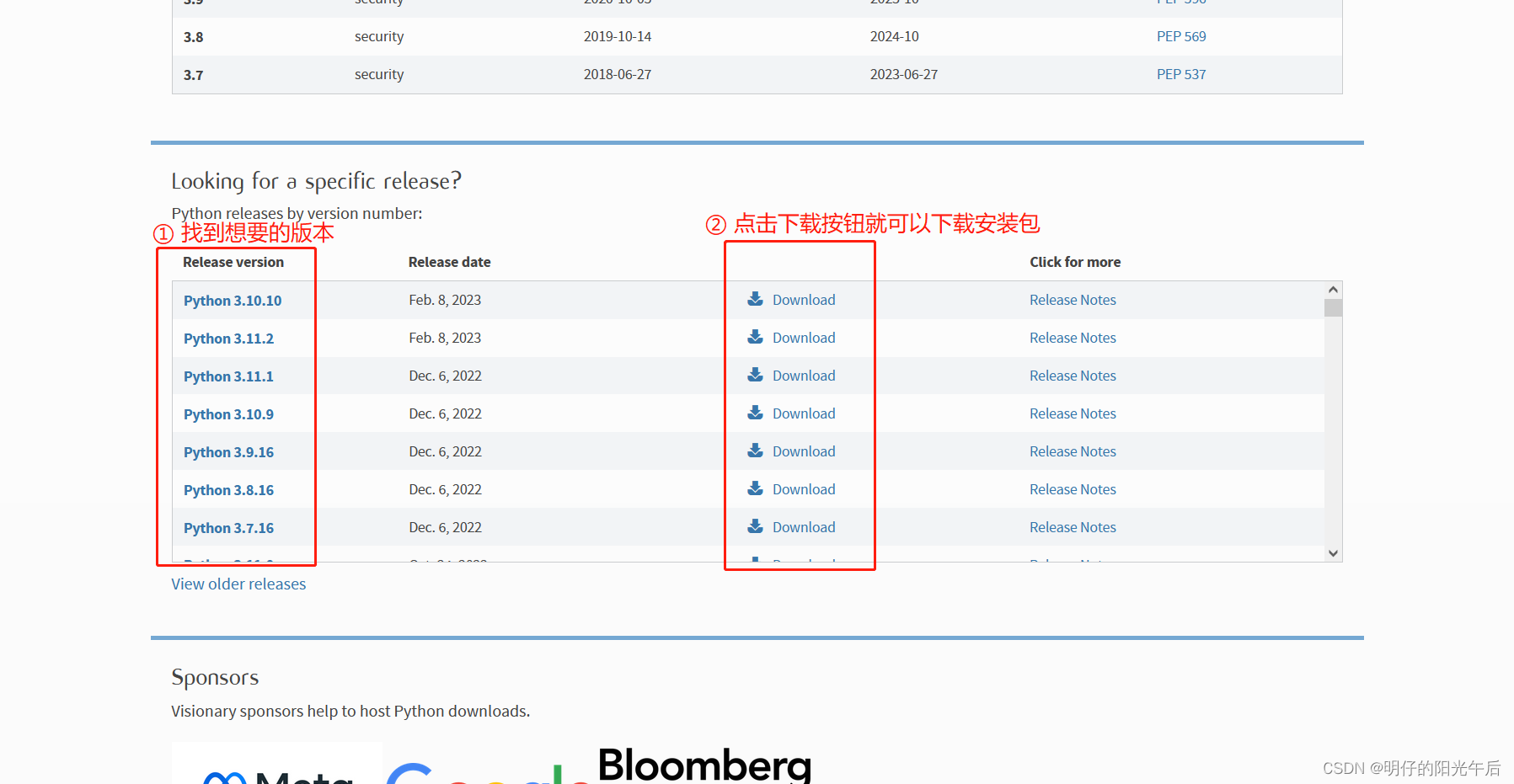
「Python|环境安装|Windows」如何在Windows上安装Python环境?
本文主要介绍如何在Windows上安装Python,帮助初学者或者非程序员伙伴快速搭建可以运行python代码的环境。 文章目录安装python做一点小配置验证python如何安装指定版本的python编程语言的环境搭建一直是学习编程的第一道门槛。 对于如何在Linux系统上安装指定版本的…...

人工智能轨道交通行业周刊-第33期(2023.2.6-2.12)
本期关键词:高铁激光清洗、高铁确认列车、无线通信系统、推理服务优化、量子信息技术 1 整理涉及公众号名单 1.1 行业类 RT轨道交通中关村轨道交通产业服务平台人民铁道世界轨道交通资讯网铁路信号技术交流北京铁路轨道交通网上榜铁路视点ITS World轨道交通联盟V…...
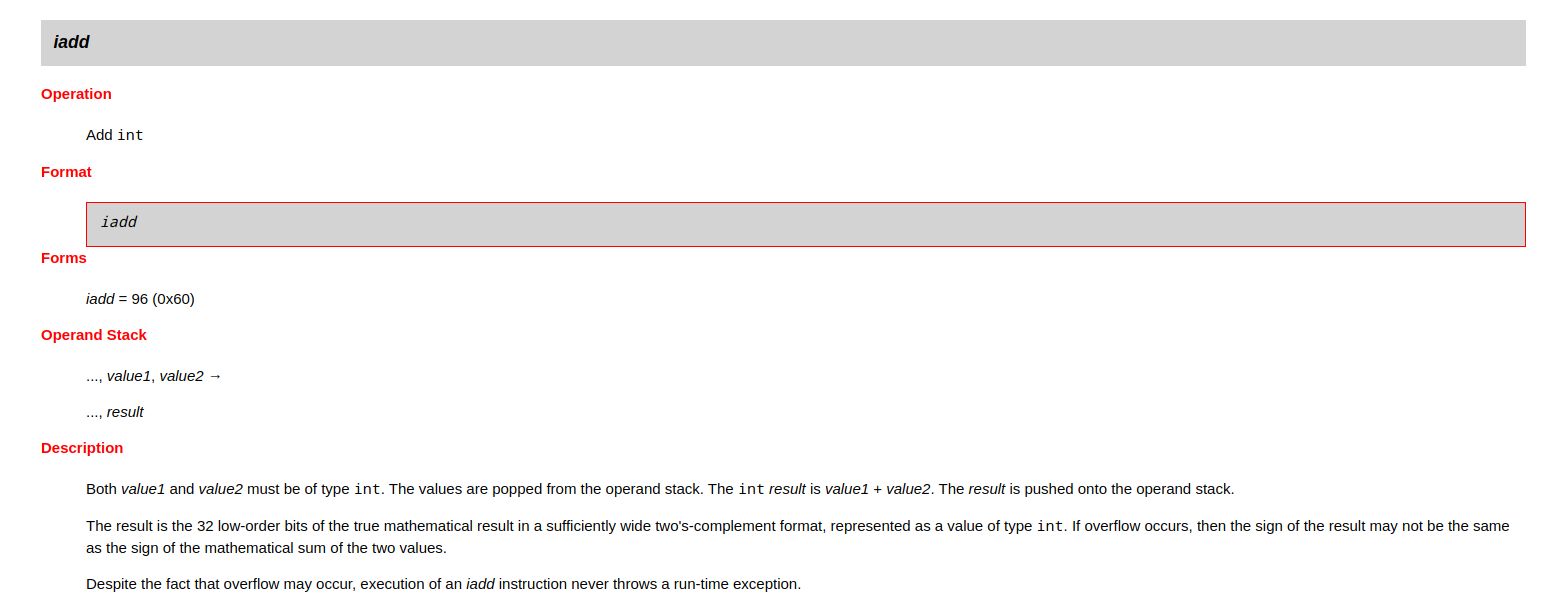
五分钟看懂Java字节码:极简手册
字节码新手很容易被厚厚的 JVM 书籍劝退,即使我看过相关书籍,工作真正用到时也全忘了,还得现学。 等我有了一定的字节码阅读经验,才发现字节码其实非常简单,只需要三步就能快速学会: 先了解 JVM 的基本结…...
C++ 类与对象(下)
✅<1>主页:我的代码爱吃辣 📃<2>知识讲解:C 🔥<3>创作者:我的代码爱吃辣 ☂️<4>开发环境:Visual Studio 2022 💬<5>前言:C类与对象的收尾工作&#…...

Java基础——I/O
一、异常 异常是程序中可能出现的问题,它的父类是Exception。异常分为两类,编译时异常、运行时异常。 编译时异常:没有继承RuntimeException的异常,直接继承于Exception。编译阶段就会错误提示。运行时异常:RuntimeE…...
关于@hide的理解
在上一篇文章《学习HandlerThread》我们提到虽然HandlerThread类里有getThreadHandler()方法得到Handler,但是我们不可能调用到它。因为这个方法用hide注释了 /*** return a shared {link Handler} associated with this thread* hide*/NonNullpublic Handler getT…...

使用python加密主机文件几种方法实现
本文主要介绍了使用python加密主机文件几种方法实现,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧数据加密是一种保护数据安全的技术,通过对数据进行编…...

西湖论剑 2023 比赛复现
WEB real_ez_node 在 route/index.js 中: router.post(/copy,(req,res)>{res.setHeader(Content-type,text/html;charsetutf-8)var ip req.connection.remoteAddress;console.log(ip);var obj {msg: ,}if (!ip.includes(127.0.0.1)) {obj.msg"only for…...

微信小程序更换管理员/重置管理员
方式1: 首先进入微信公众平台官网进入并登录后在管理中找到成员管理选项找到管理员点击后方的修改选项需要使用原管理员的微信进行扫码验证扫码后在手机上确认绑定新管理员,注意:如果是个人账号不可以更改成其他人。 方式2:原管…...
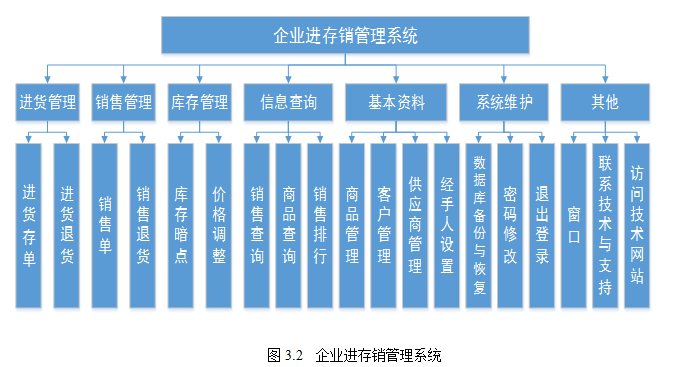
企业进存销管理系统
技术:Java、JSP等摘要:随着当今世界计算机技术的飞速发展,计算机在企业管理中应用的普及,利用计算机实现企业进销存管理势在必行。本系统结合公司实际的进销存制度,通过对本公司的供应商、客户、商品、进货、销售、进销…...
C++入门
变量变量创建的语法: 数据类型 变量名 变量初始值;int a 10;cout << a << endl;常量作用:用于记录程序中不可更改的教国C定义常量两种方式1).#define 宏常量:#define 常量名 常量值通常在文件上方定义。表示一个常量2).const 修饰的变量const 数据类型 常量名 常…...
- H264码流如何在SPS中获取宽高信息?)
视频知识点(20)- H264码流如何在SPS中获取宽高信息?
《音视频开发》系列-总览 前沿 了解H264视频编码格式的小伙伴都知道,H264编码中存在两个非常重要的参数集。没错,它们就是序列参数集(SPS)和图像参数集(PPS),而且通常情况下,PPS会依赖SPS中的部分参数信息,同时,视频码流的宽高信息也存储在SPS中。那么如何从中获取视…...
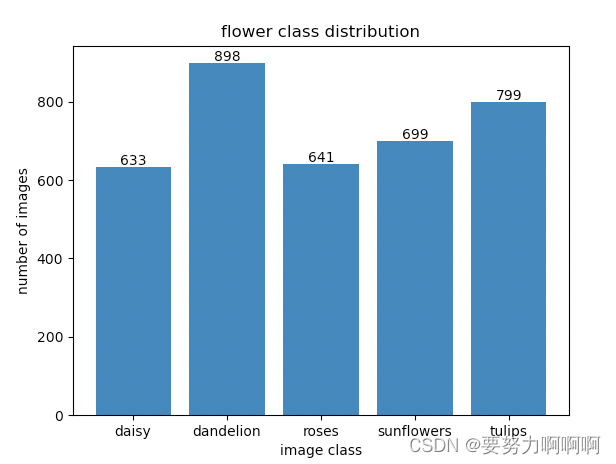
鲜花数据集实验结果总结
从read_split_data中得到:训练数据集,验证数据集,训练标签,验证标签。的所有的具体详细路径 数据集位置:https://download.csdn.net/download/guoguozgw/87437634 import os #一种轻量级的数据交换格式, …...
ElasticJob-Lite架构篇 - 认知分布式任务调度ElasticJob-Lite
前言 本文基于 ElasticJob-Lite 3.x 版本展开分析。 如果 Quartz 集群中有多个服务端节点,任务决定在哪个服务端节点上执行的呢? Quartz 采用随机负载,通过 DB 抢占下一个即将触发的 Trigger 绑定的任务的执行权限。 在 Quartz 的基础上&…...

【直击招聘C++】2.6 对象之间的复制
2.6 对象之间的复制一、要点归纳1. 对象之间的复制操作1.1 运算符1.2 拷贝构造函数2. 对象之间的浅复制和深复制2.1 对象的浅复制2.2 对象的深复制二、面试真题解析面试题1面试题2一、要点归纳 1. 对象之间的复制操作 同一个类的对象之间可以进行复制操作,即将一个…...

学了这么久python,不会连自己啥python版本都不知道吧?
人生苦短,我用Python 源码资料电子书:点击此处跳转文末名片获取 查看 Python 版本 我们可以在命令窗口(Windows 使用 winR 调出 cmd 运行框)使用以下命令查看我们使用的 Python 版本: python -V 或 python --version 以上命令执行结果如下: …...

Revive:从间谍软件进化成银行木马
2022 年 6 月,Cleafy 研究人员发现了一个新的安卓银行木马 Revive。之所以选择 Revive 这个名称,是因为恶意软件为防止停止工作启用的一项功能名为 revive。 Revive 属于持续潜伏的那一类恶意软件,因为它是为特定目标开发和定制的。这种类型…...
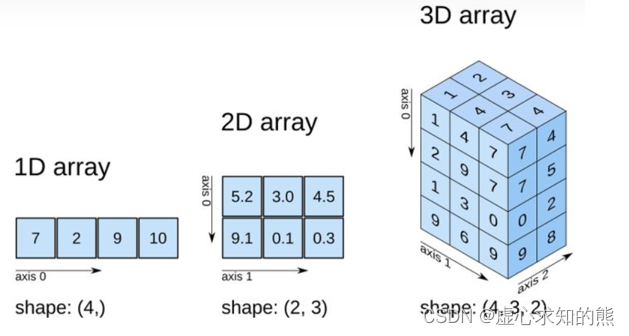
Python 之 NumPy 简介和创建数组
文章目录一、NumPy 简介1. 为什么要使用 NumPy2. NumPy 数据类型3. NumPy 数组属性4. NumPy 的 ndarray 对象二、numpy.array() 创建数组1. 基础理论2. 基础操作演示3. numpy.array() 参数详解三、numpy.arange() 生成区间数组四、numpy.linspace() 创建等差数列五、numpy.logs…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...


