二叉排序树的创建、插入、查找和删除【数据结构】
二叉排序树
- 若它的左子树不空,则左子树上所有结点的值均小于它根结点的值。
- 若它的右子树不空,则右子树上所有结点的值均大于它根结点的值。
- 它的左、右树又分为⼆叉排序树
二叉排序树也叫二叉查找树、二叉搜索树
二叉排序树的创建、插入、查找和删除
创建和插入
题目描述
给出一个数据序列,建立二叉排序树,并实现插入功能。
在建立和插入操作后,都输出二叉树的先序遍历结果i
输入
第1行输入n,表示序列包含n个数据
第2行输入n个数据,都是自然数且互不相同,数据之间用空格隔开
第3行输入m,表示要插入m个数据
输入m行,每行一个要插入的数据,都是自然数且和前面的数据不等
输出
第一行输出一开始构建的二叉排序树的先序遍历结果
从第二行起,输出m行,每行输出插入一个数据到二叉排序树后的先序遍历结果
每行输出的遍历结果中,每个数据后面都带一个空格,最后一个数据也带。
输入样例1
6
22 33 55 66 11 44
3
77
50
10
输出样例1
22 11 33 55 44 66
22 11 33 55 44 66 77
22 11 33 55 44 50 66 77
22 11 10 33 55 44 50 66 77
输入样例2
6
33 55 22 66 11 44
3
25
88
50
输出样例2
33 22 11 55 44 66
33 22 11 25 55 44 66
33 22 11 25 55 44 66 88
33 22 11 25 55 44 50 66 88
#include<bits/stdc++.h>
using namespace std;
//树节点
struct tree
{int value=0;tree* left=NULL;tree* right=NULL;
};
//插入操作
tree* insert(tree* t,int a)
{tree* root=t;while(1){if(t->value==0) {t->value=a;break;}if(a<t->value) {if(!t->left) t->left=new tree;t=t->left;}else {if(!t->right) t->right=new tree;t=t->right; }}return root;
}
//先序遍历
void prior(tree* t)
{if(t==NULL) return ;cout<<t->value<<" ";prior(t->left);prior(t->right);
}
int main()
{int n;cin>>n;tree* root=new tree;for(int i=0;i<n;i++){int x;cin>>x;root=insert(root,x);}prior(root);cout<<endl;int m;cin>>m;for(int i=0;i<m;i++) {int x;cin>>x;//插入root=insert(root,x);prior(root);cout<<endl;}return 0;
}
查找
题目描述
给出一个数据序列,建立二叉排序树,并实现查找功能
输入
第1行输入n,表示首个序列包含n个数据
第2行输入n个数据,都是自然数且互不相同,数据之间用空格隔开
第3行输入m,表示要查找m个数据
接着输入m行,每行一个要查找的数据,都是自然数
以此类推输入下一个示例
输出
第一行输出有序的数据序列,对二叉排序树进行中序遍历可以得到
从第二行起,输出查找结果,如果查找成功输出查找次数,如果查找失败输出-1
输入样例1
6
22 33 55 66 11 44
7
11
22
33
44
55
66
77
输出样例1
11 22 33 44 55 66
2
1
2
4
3
4
-1
输入样例2
6
33 22 55 11 66 44
4
88
11
44
66
输出样例2
11 22 33 44 55 66
-1
3
3
3
#include<bits/stdc++.h>
using namespace std;
//树节点
struct tree
{int value=0;tree* left=NULL;tree* right=NULL;
};
//插入
tree* insert(tree* t,int a)
{tree* root=t;while(1){if(t->value==0) {t->value=a;break;}if(a<t->value) {if(!t->left) t->left=new tree;t=t->left;}else {if(!t->right) t->right=new tree;t=t->right; }}return root;
}
//中序遍历
void middle(tree* t)
{if(t==NULL) return ;middle(t->left);cout<<t->value<<" ";middle(t->right);
}
//查找
int find(tree* t,int a,int time)
{while(1){time++;if(t->value==0){time=-1;break;}if(t->value==a) break;if(a<t->value){if(!t->left) t->left=new tree;t=t->left;}else{if(!t->right) t->right=new tree;t=t->right;}}return time;
}
int main()
{int n;cin>>n;tree* root=new tree;for(int i=0;i<n;i++){int x;cin>>x;root=insert(root,x);}middle(root);cout<<endl;int m;cin>>m;for(int i=0;i<m;i++){int x;cin>>x;cout<<find(root,x,0)<<endl;}return 0;
}
删除
题目描述
给出一个数据序列,建立二叉排序树,并实现删除功能
对二叉排序树进行中序遍历,可以得到有序的数据序列
输入
第一行输入t,表示有t个数据序列
第二行输入n,表示首个序列包含n个数据
第三行输入n个数据,都是自然数且互不相同,数据之间用空格隔开
第四行输入m,表示要删除m个数据
从第五行起,输入m行,每行一个要删除的数据,都是自然数
以此类推输入下一个示例
输出
第一行输出有序的数据序列,对二叉排序树进行中序遍历可以得到
从第二行起,输出删除第m个数据后的有序序列,输出m行
以此类推输出下一个示例的结果
输入样例1
1
6
22 33 55 66 11 44
3
66
22
77
输出样例1
11 22 33 44 55 66
11 22 33 44 55
11 33 44 55
11 33 44 55
提示
当删除数据不在序列中,那么删除操作等于不执行,所以输出序列不变化
- 被删除的节点是叶子节点,将双亲节点中相应的指针域的值改为空
- 被删除的节点只有左子树或右子树,将要删除的节点的双亲节点相应指针域的值指向被删除节点的左子树或者右子树
- 被删除节点既有左子树又有右子树,将左子树中的最大值或者右子树中的最小值代替该节点
#include<bits/stdc++.h>
using namespace std;
//树节点
struct tree
{int value=0;tree* left=NULL;tree* right=NULL;
};
//插入
tree* insert(tree* t,int a)
{tree* root=t;while(1){if(t->value==0) {t->value=a;break;}if(a<t->value) {if(!t->left) t->left=new tree;t=t->left;}else {if(!t->right) t->right=new tree;t=t->right; }}return root;
}
//中序遍历
void middle(tree* t)
{if(t==NULL||t->value==0) return ;middle(t->left);cout<<t->value<<" ";middle(t->right);
}
//删除
void del(tree* t,int a)
{//记录父节点tree* p=NULL;while(1){if(t->value==0) break;if(t->value==a){//叶子结点直接删除if(!t->left&&!t->right){if(p->left==t) p->left=NULL;else p->right=NULL;break;}//只有左子树或只有右子树if(!t->left||!t->right){//左子树不空if(t->left){if(p->left==t) p->left=t->left;else p->right=t->left;break;}//右子树不空if(t->right){if(p->left==t) p->left=t->right;else p->right=t->right;break;}}//左右子树都不空//本做法是用左子树最大值代替该节点值tree* now=t->left;tree* par=t;while(now->right) {par=now;now=now->right;}//左子树最大值int value=now->value;//更新值t->value=value;//这里注意!!!if(!now->left&&!now->right) {//直接删除左子树的根节点if(par==t) par->left=NULL;//删除的不是左子树的根节点else par->right=NULL;}//有子节点肯定是左子节点else par->right=now->left;break;}if(a<t->value){if(!t->left) t->left=new tree;p=t;t=t->left;}else{if(!t->right) t->right=new tree;p=t;t=t->right;}}
}
int main()
{int t;cin>>t;for(int i=0;i<t;i++){int n;cin>>n;tree* root=new tree;for(int i=0;i<n;i++){int x;cin>>x;root=insert(root,x);}middle(root);cout<<endl;int m;cin>>m;for(int i=0;i<m;i++) {int x;cin>>x;del(root,x);middle(root);cout<<endl;}}return 0;
}相关文章:

二叉排序树的创建、插入、查找和删除【数据结构】
二叉排序树 若它的左子树不空,则左子树上所有结点的值均小于它根结点的值。若它的右子树不空,则右子树上所有结点的值均大于它根结点的值。它的左、右树又分为⼆叉排序树 二叉排序树也叫二叉查找树、二叉搜索树 二叉排序树的创建、插入、查找和删除 …...

【管理篇 / 恢复】❀ 07. macOS下用命令刷新固件 ❀ FortiGate 防火墙
【简介】随着苹果电脑的普及,很多管理员都会通过苹果电脑对飞塔防火墙进行管理。当防火墙需要命令状态下刷新固件时,在macOS下用命令刷新固件,将会是一个小小的挑战。 首先是硬件的连接,USB配置线的USB一头,接入MAC的U…...

工作纪实40-使用redis的几种姿势
线上查问题看某个redis的key值,记录一下 1.直接使用telnet进行连接(贼拉方便) telnet ip port > auth pwd1.模糊查询 scan 0 MATCH abc* 2.查看所有key keys * 3.ttl key 查看key的ttl2.使用redis-cli连接(费劲吧啦,还需要本地…...

修改 docker /dev/shm 的大小
修改 docker /dev/shm 的大小 1,获取完整id: docker inspect 245| grep Id rootlynxi:~# docker inspect 245| grep Id"Id": "245ab167ed9a79873b31b3a38df2053870fe72f267c3c1a660df25c63e37e88b",2,修改 ShmSize&…...

【观察】Aginode安捷诺:坚守“长期主义”,服务中国数字经济
毫无疑问,随着整个社会加速数字化转型,尤其是5G、人工智能、大数据等技术兴起,以及智慧医疗、智慧金融、智能制造等应用加速落地,算力网络在经济社会发展中扮演了愈来愈重要的角色,成为支撑数字经济蓬勃发展的“新引擎…...

HttpClient库与代理IP在爬虫程序中的应用
目录 前言 一、HttpClient库的基本使用方法 二、代理IP的使用方法 三、代理IP池的使用方法 四、总结 前言 在编写爬虫程序时,我们经常会使用HttpClient库来发送HTTP请求,获取网页内容。然而,有些网站可能会对频繁的请求进行限制&#x…...
C#最佳工具集合:IDE、分析、自动化工具等
C#是企业中广泛使用的编程语言,特别是那些依赖微软的程序语言。如果您使用C#构建应用程序,则最有可能使用Visual Studio,并且已经寻找了一些扩展来对您的开发进行管理。但是,这个工具列表可能会改变您编写C#代码的方式。 C#编程的…...
promethues grafana 安装和使用
文章目录 1、promethues安装2、node-exporter安装3、grafana安装4、配置promethues监控node节点5、grafana操作外传 Docker 镜像下载地址: https://hub.docker.com 比较好的hub.docker.com///-- https://hub.docker.com/u/bitnami grafana监控面板:https…...

华为DriveONE电机控制器拆解实拍
如果说之前的问界M5、M7,华为让我们看到其在智能化上确实拥有遥遥领先的能力,那么在智界S7上,则让我们看到华为在动力、底盘这些硬件执行层面,竟然也有不输给很多车企的实力。1、华为电驱,全球第一?在智界S…...
)
【git使用】历史commit的分割(git rebase和 git reset的联合使用)
参考 [译] 分割一个已存在的 git commit - 掘金Git - 重写历史idea git如何撤回提交 - PingCodegit 工作原理与撤销操作图解 | Shall We Code? 分割一个已存在的 git commit Git 与其他版本控制系统的主要区别之一,在于其允许用户重写历史。实现这一目的的主要途…...

栈和队列oj题——225. 用队列实现栈
** 个人主页:晓风飞 专栏: 数据结构| Linux|| C语言 路漫漫其修远兮,吾将上下而求索 文章目录 题目要求:实现 MyStack 类:注意:示例:解释:提示: 解题核心数据结构的定义初…...
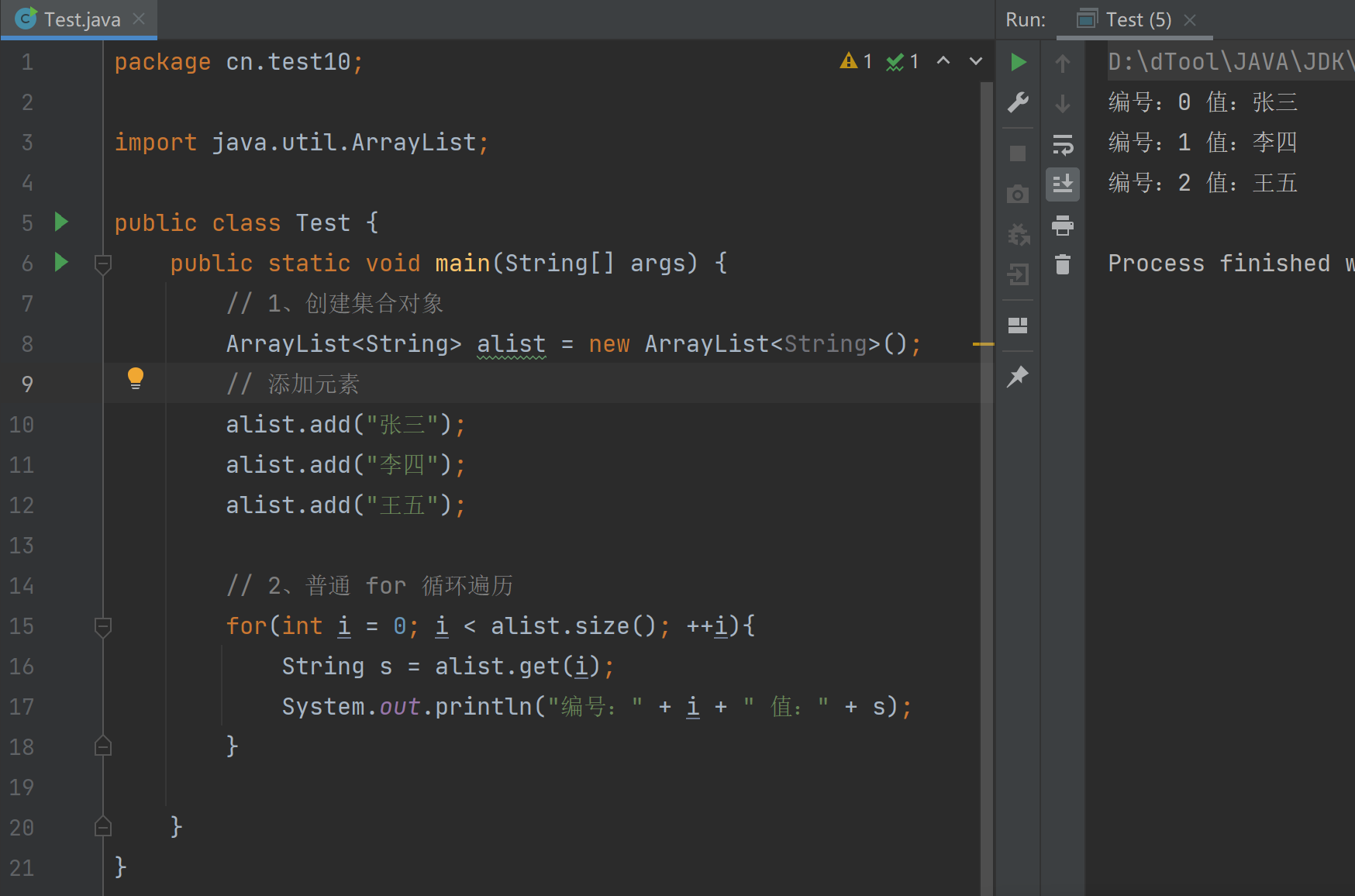
集合的三种遍历方式
迭代器(Iterator) 概述:Iterator 是个接口,迭代器是集合的专用遍历方式 使用方法,我们想要使用迭代器,必须首先得到集合对象,通过集合对象生成迭代器对象,才能进行集合的遍历 常用…...

Mysql 中的常用命令
在数字化世界中,数据库已经成为数据存储和处理的核心。而MySQL,作为最受欢迎的关系型数据库管理系统之一,其强大的功能和易用性使它成为开发者和企业的首选。掌握MySQL中的常用命令,是每一位数据库管理员和开发者的基本要求。本篇…...

【Java】CompletableFuture使用方法
背景 CompletableFuture是Java 8中引入的一个类,它实现了Future和CompletionStage接口,用于表示异步计算的结果。使用CompletableFuture可以方便地编写异步编程的代码,并且可以链式地组合多个异步操作。 接口 CompletableFuture实现了Future…...

摆烂式学习ssh
摆烂式学习ssh ssh工作原理ssh基本使用sshd配置文件密钥登录1.客户端2.服务器3.注意事项4.使用密钥登录测试 ssh高级使用技巧1.在非正规端口启动2.rsync 命令3.透过 ssh 通道加密原本无加密的服务4.以ssh信道配合x server 传递图形接口5.ssh配合virtualbox虚拟机使用技巧 ssh工…...

用 Python 抓取 bilibili 弹幕并分析!
01 实现思路 首先,利用哔哩哔哩的弹幕接口,把数据保存到本地。接着,对数据进行分词。最后,做了评论的可视化。 02 弹幕数据 平常我们在看视频时,弹幕是出现在视频上的。实际上在网页中,弹幕是被隐藏在源代码…...
)
目标检测YOLO实战应用案例100讲-基于红外图像处理的无人机光伏组件故障检测(续)
目录 3.2 自适应温度阈值故障检测算法设计 3.3 基于拟合灰度曲线的故障检测方案设计...

go mod 命令详解
文章目录 1.关于模块2.关于 go mod3.格式4.示例参考文献 1.关于模块 模块(Modules)是 Go 1.11 版本引入的一依赖管理机制。 一个模块是 Go packages 的集合,定义在项目根目录下的 go.mod 文件。go.mod 文件定义了模块的路径,这也…...

花了一小时,拿python手搓了一个考研背单词软件
听说没有好用的电脑端背单词软件?只好麻烦一下,花了一小时,拿python手搓了一个考研背单词软件。 代码已经开源在我的github上,欢迎大家STAR! 其中,数据是存放在sqlite中,形近词跳转是根据jaro …...

一篇文章学会Vim
一篇文章学会Vim 声明:以下内容均为我个人的理解,如果发现错误或者疑问可以联系我共同探讨 简介 Vim是一个高度可定制的终端文本编辑器,它可以很方便的创建和修改任何类型的文本。作为vi的升级版,有许多新的特性(以下列出的特性…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...

基于 HTTP 的单向流式通信协议SSE详解
SSE(Server-Sent Events)详解 🧠 什么是 SSE? SSE(Server-Sent Events) 是 HTML5 标准中定义的一种通信机制,它允许服务器主动将事件推送给客户端(浏览器)。与传统的 H…...
