【数据结构】二叉树的链式实现
树是数据结构中非常重要的一种,在计算机的各方个面都有他的身影
此篇文章主要介绍二叉树的基本操作
目录
- 二叉树的定义:
- 二叉树的创建:
- 二叉树的遍历:
- 前序遍历:
- 中序遍历:
- 后序遍历:
- 二叉树节点个数:
- 二叉树叶子结点个数:
- 二叉树第k层节点个数:
- 二叉树查找值为x的节点:
- 二叉树的销毁:
二叉树的定义:
这里我们使用char,因为二叉树的创建我们会使用递归创建,需要传入一个字符串进行操作
typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
二叉树的创建:
我们通过前序遍历的数组"123###45##6##"构建二叉树
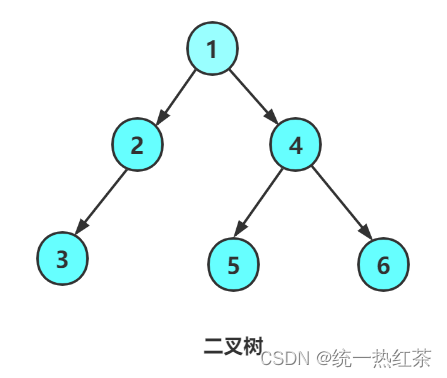
这里讲一下我使用递归做题时的一些做题感受方法:
- 首先写出递归的结束条件,这是每个递归都不可以缺少的
- 利用分治的思想(将一个问题分成几个相同的子问题)
- 把你的递归想象是可以完成你既定的任务
- 写出你调用这个递归需要本次进行的工作
- 完成后可以画出一个递归展开图进行验证
接下来我会仔细带着大家仔细领悟,熟能生巧,同学们一定不要气馁
先解释一下这个函数传参的意义:
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
a就是我们传参的字符数组
pi是我们字符数组的下标,为什么需要下标的地址呢,因为形参的改变不会影响实参
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{if (a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc fail");return;}root->data = a[(*pi)++];root->left = BinaryTreeCreate(a, pi);root->right = BinaryTreeCreate(a, pi);return root;
}
- 做递归时截止条件是必不可少的,我们选择使用叶子节点是否为空作为判断标准。
- 我们将这个问题从创建一个完整二叉树分成先创建一个节点并连接他的左右节点的问题·
- 我们现在需要完成此时函数需要完成的任务,此次函数的目的是创造一个二叉树,我们需要对
root->val进行赋值,再将root的左右子树进行连接 - 此时观察整个函数,我们发现我们已经生成了一个
root节点,也进行了赋值,root的左右节点也都分别使用BinaryTreeCreate(a, n, pi)这个函数进行连接,我们已经把此函数当做可以完成既定任务的,不需要过多纠结,此时我们在加一个返回值root,就完成了此次函数的创建
二叉树的递归图:
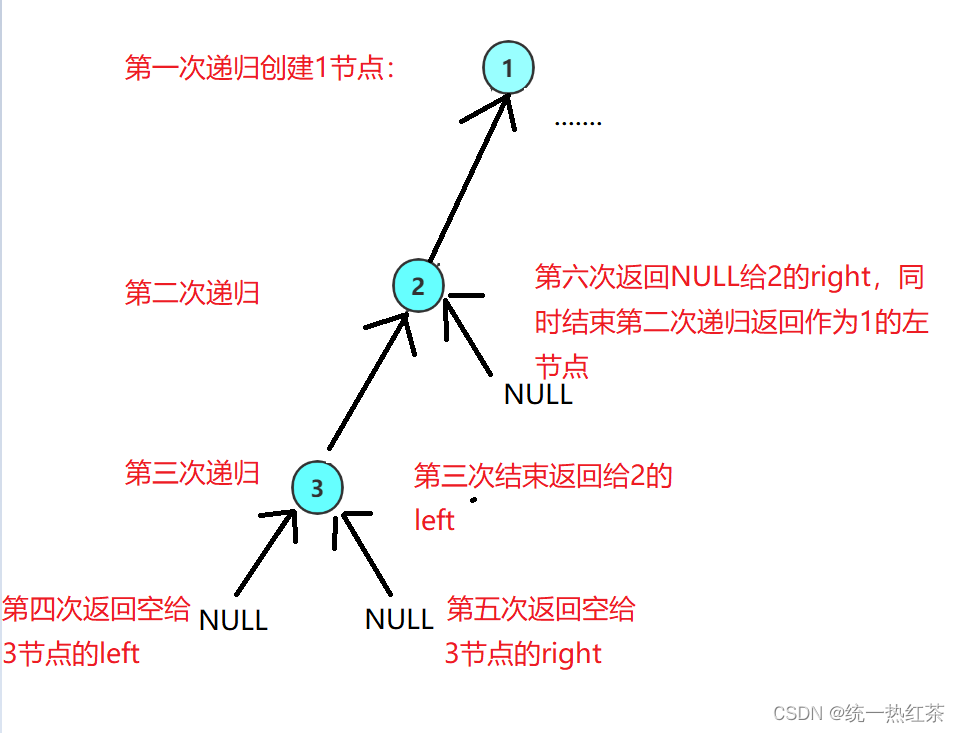
大家也可以自己动手画一下递归展开图
二叉树的遍历:
前序遍历:
有了以上的思路就可以很简单的实现了
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%c ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}
代码也很简洁
- NULL结束条件
- 分治:前序是根左右的遍历,故我们先遍历根,在遍历左子树右子树
- 没有返回值,不需要return
就像下图这样,将这个程序当成可以完成任务的函数。printf("%c ", root->data);//进行本次的任务BinaryTreePrevOrder(root->left);//遍历左子树BinaryTreePrevOrder(root->right);//遍历左子树
中序遍历:
与前序遍历一致
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BinaryTreePrevOrder(root->left);printf("%c ", root->data);BinaryTreePrevOrder(root->right);
}
后序遍历:
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);printf("%c ", root->data);
}
二叉树节点个数:
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
- 结束条件为
NULL - 分治:将这个问题当成当前节点+左子树节点与右子树节点
- return 当前节点+左子树节点与右子树节点
二叉树叶子结点个数:
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
- 结束条件有两个(因为当前节点不为空节点才能是叶子节点),为空或为叶子节点
- 分治:将问题变为左子树的叶子节点与右子树的叶子结点
- 返回总结点个数
二叉树第k层节点个数:
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
1.结束条件有两个,当为NULL或为目标层数时为结束
2. 分治:这个的分治并不像上边的简单了,我们需要root的第k层转化为root->左子树的k-1层与root->right的k-1层,将K也作为函数传参,每次减1
3. 返回第k层节点个数
二叉树查找值为x的节点:
我们先来看这样一段代码,相信有许多小伙伴在遇到
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BinaryTreeFind(root->left, x);BinaryTreeFind(root->right, x);return NULL;
}
乍一看好像没什么问题,不就是前序遍历嘛,
不然,实则我们并没有记录找到的地址,像下图一样
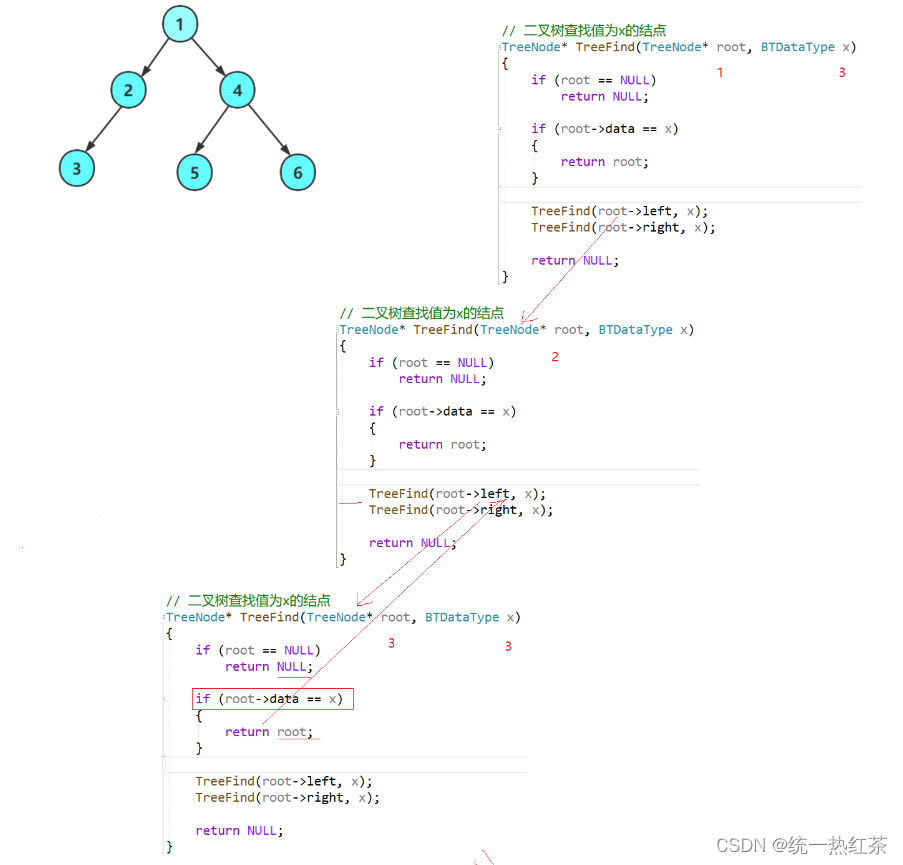
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1){return ret1;}BTNode* ret2 = BinaryTreeFind(root->right, x);if (ret2){return ret2;}return NULL;
}
- 结束为
NULL或目标值 - 分治:当前节点+左子树+右子树进行前序遍历
- 记录
ret值并返回
二叉树的销毁:
使用后序遍历,因为前序与中序需要记录当前被销毁的左右节点地址
void BinaryTreeDestory(BTNode* root)
{if (root == NULL){return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);
}
持续更新中…
相关文章:

【数据结构】二叉树的链式实现
树是数据结构中非常重要的一种,在计算机的各方个面都有他的身影 此篇文章主要介绍二叉树的基本操作 目录 二叉树的定义:二叉树的创建:二叉树的遍历:前序遍历:中序遍历:后序遍历: 二叉树节点个数…...
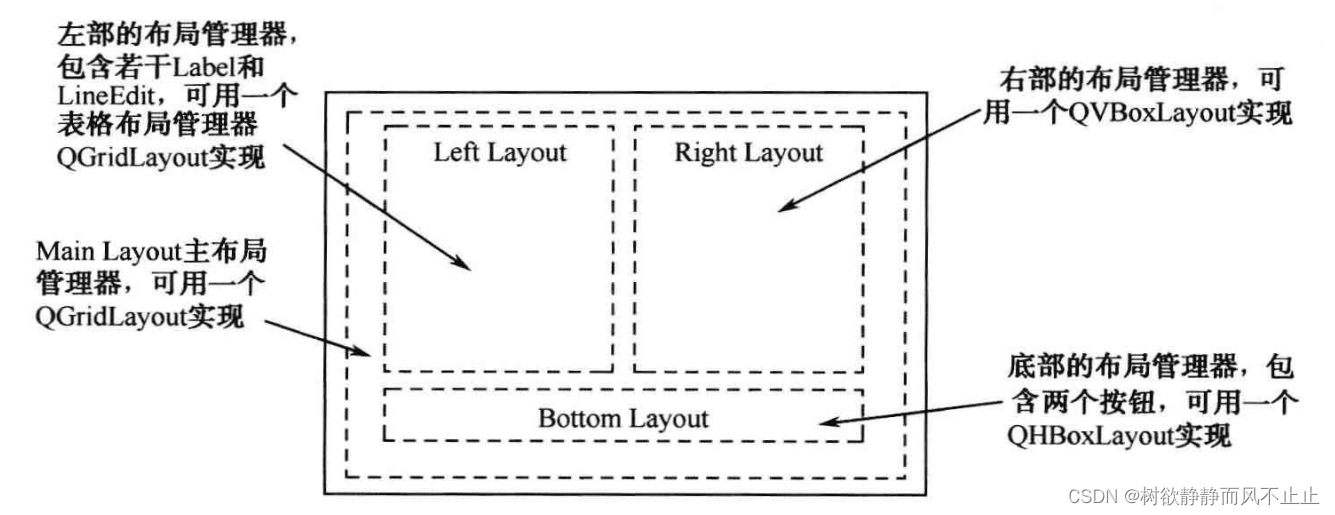
八、QLayout 用户基本资料修改(Qt5 GUI系列)
目录 一、设计需求 二、实现代码 三、代码解析 四、总结 一、设计需求 在很多应用程序中会有用户注册或用户编辑信息等界面。本文就设计一个用户信息编辑界面。要求包含用户名、姓名、性别、部门、年龄、头像、个人说明等信息。 二、实现代码 #ifndef DIALOG_H #define D…...

tomcat、java、maven
JDK|JRE Tomcat官网介绍的更清楚 Java 环境安装 安装 wget https://builds.openlogic.com/downloadJDK/openlogic-openjdk/8u392-b08/openlogic-openjdk-8u392-b08-linux-x64.tar.gz tar -xf openlogic-openjdk-8u392-b08-linux-x64.tar.gz mv openlogic-openjdk…...

IDEA好用插件
CodeGlance Pro 右侧代码小地图 Git Commit Template git提交信息模板 IDE Eval Reset 无限试用IDEA Maven Helper 图形化展示Maven项 One Dark theme 好看的主题 SequenceDiagram 展示方法调用链 Squaretest 生成单元测试 Translation 翻译 Lombok lombok插件…...
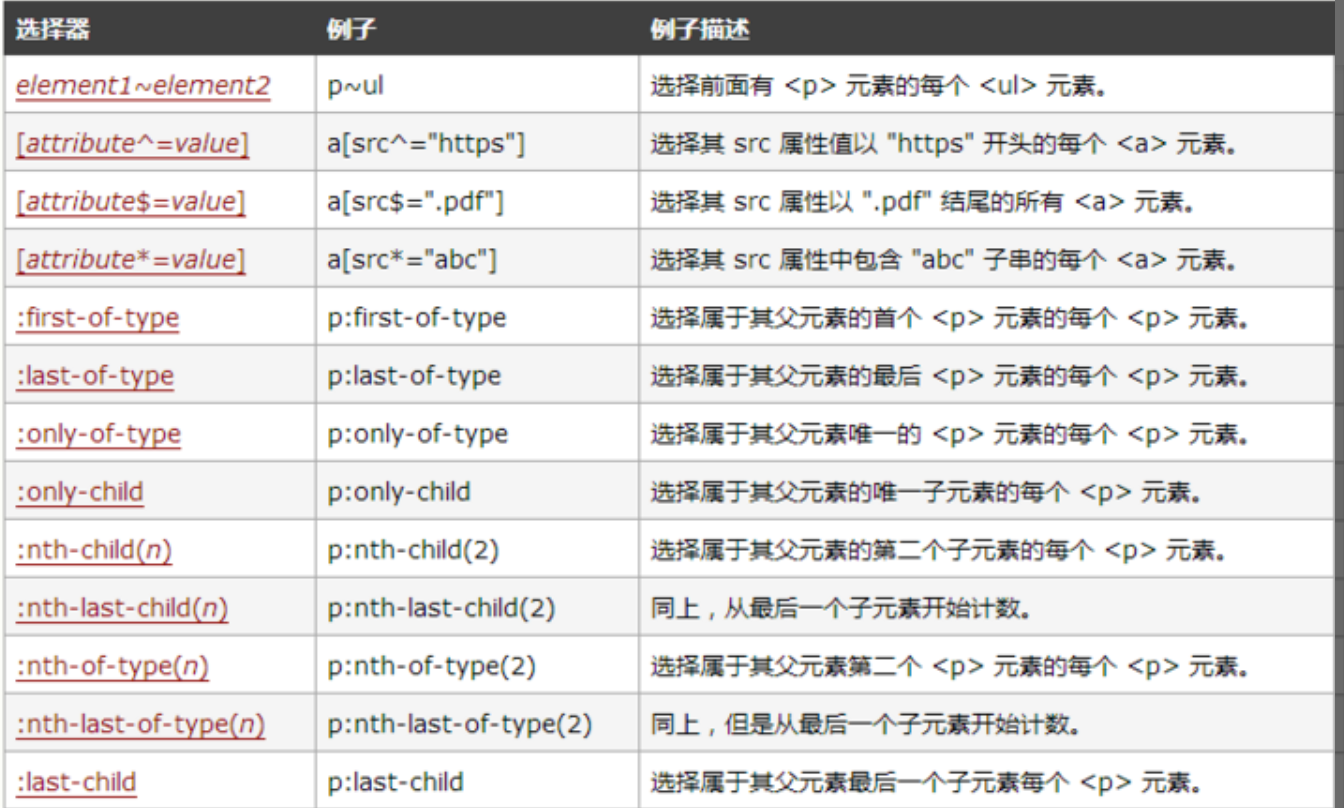
面试官:CSS3新增了哪些新特性?
面试官:CSS3新增了哪些新特性? 一、是什么 css,即层叠样式表(Cascading Style Sheets)的简称,是一种标记语言,由浏览器解释执行用来使页面变得更美观 css3是css的最新标准,是向后兼…...

Vite5 + Vue3 + Element Plus 前端框架搭建
为了开发一套高效使用的 Vite5 + Vue3 + Element Plus 前端框架,你可以按照以下步骤进行。话不多说,先上演示地址:Vue Shop Vite。 1, 安装开发环境 开发之前,确保你的电脑已经安装了 Node.js(建议使用最新稳定版 LTS),然后安装 Vite CLI。在命令行中运行以下命令: …...

STM32 内部 EEPROM 读写
STM32 的某些系列 MCU 自带 EEPROM。笔者使用的 STM32L151RET6 自带 16 KB 的 EEPROM,可以用来存储自定义的数据。在芯片选型时,自带 EEPROM 也可以作为一个考量点,省去了在外接 EEPROM 的烦恼。 下面简单介绍下 STM32 内部 EEPROM 的读写流…...
)
androidStudio sync failed GradlePropertiesModel (V2)
大家在增加模块的时候经常遇到吧?重启后就好了。 Cannot get GradlePropertiesModel (V2) for project ‘GradleProject{path’:app’}’ 然而,今天开机以后,无论如何,点击gradle的大象图标(Sync Project with Gradle Files)&…...

结构方程模型(SEM)
结构方程模型(Structural Equation Modeling)是分析多变量间因果关系的利器,在众多学科领域具有巨大应用潜力。我们前期推出的《基于R语言结构方程模型》课程通过结构方程原理介绍、结构方程全局和局域估计、模型构建和调整、潜变量分析、复合…...

基于UDP的网络编程
UDP服务端 #ifdef _WIN32 #define _WINSOCK_DEPRECATED_NO_WARNINGS #define close closesocket #include <winsock2.h> #else #include <arpa/inet.h> #include <netdb.h> #include <netinet/in.h> #in…...

vue判断组件有没有传入的slot有就渲染slot没有就渲染内部节点
GPT4国内站点:海鲸AI 在 Vue 中,你可以使用 $slots 对象来检查是否有特定的插槽内容被传递给组件。Vue 3 中的 $slots 是一个对象,其中包含了所有插槽的引用。如果插槽没有内容,对应的插槽属性将会是 undefined。 下面是一个例子…...
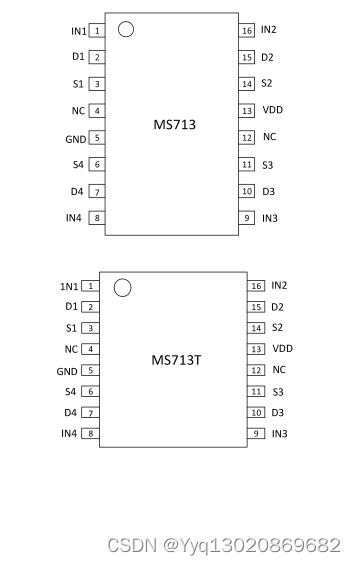
MS713/MS713T:CMOS 低压、4Ω四路单刀单掷开关,替代ADG713
产品简述 MS713/MS713T 是一款单芯片 CMOS 4 路可选择开关,具有低 功耗、高开关速度、低导通阻抗、低漏电和高带宽特性。其工作 电压范围是 1.8V 到 5.5V ,可以广泛应用在电池供电仪器仪表、新 一代的模数转换和数模转换系统中。其高带宽特性可用在 …...

Android 内容生成pdf文件
1.引入itext7 implementation com.itextpdf:itext7-core:7.1.13上面比较大,可以直接下载需要集成的jar包 implementation files(libs\\layout-7.1.13.jar) implementation files(libs\\kernel-7.1.13.jar) implementation files(libs\\io-7.1.13.jar) implementatio…...

Javaweb-日程管理
094.日程管理第二期_准备数据库和实体类_哔哩哔哩_bilibili navicat 下载 学生认证: Navicat 教育版 - 学生许可证 | Navicat navicat连接mysql 使用navicat连接mysql数据库创建数据库、表、转储sql文件,导入sql数据_哔哩哔哩_bilibili...

SwiftUI之深入解析如何创建一个灵活的选择器
一、前言 在 Dribbble 上找到的设计的 SwiftUI 实现时,可以尝试通过一些酷炫的筛选器扩展该项目以缩小结果列表。筛选视图将由两个独立的筛选选项组成,两者都有一些可选项可供选择。但是,在使用 UIKit 时,总是将这种类型的视图实…...
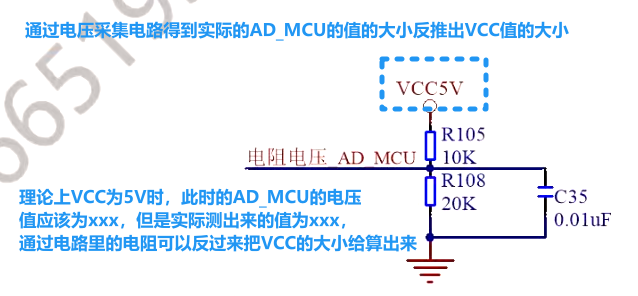
【模拟量采集1.2】电阻信号采集
【模拟量采集1.2】电阻信号采集 1 怎么测?2 测输入电阻电压即转为测模拟电压值,这里需要考虑选用怎样的辅助电阻?3 实际电路分析3.1 在不考虑 VCC-5V 电压的纹波等情况时(理想化此时输入的 VCC 就是稳定的 5V)3.2 若考…...
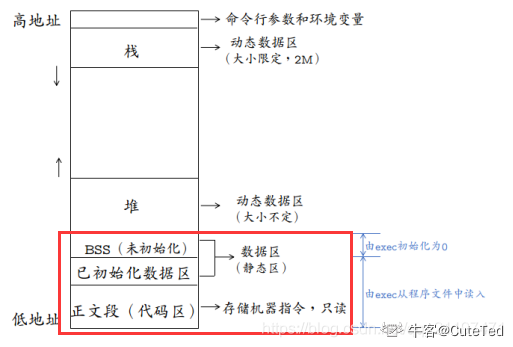
c++牛客总结
一、c/c语言基础 1、基础 1、指针和引用的区别 指针是一个新的变量,指向另一个变量的地址,我们可以通过这个地址来修改该另一个变量; 引用是一个别名,对引用的操作就是对变量本身进行操作;指针可以有多级 引用只有一…...
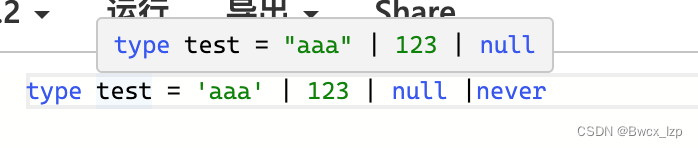
ts相关笔记(基础必看)
推荐一下小册 TypeScript 全面进阶指南,此篇笔记来源于此,记录总结,加深印象! 另外,如果想了解更多ts相关知识,可以参考我的其他笔记: vue3ts开发干货笔记TSConfig 配置(tsconfig.…...
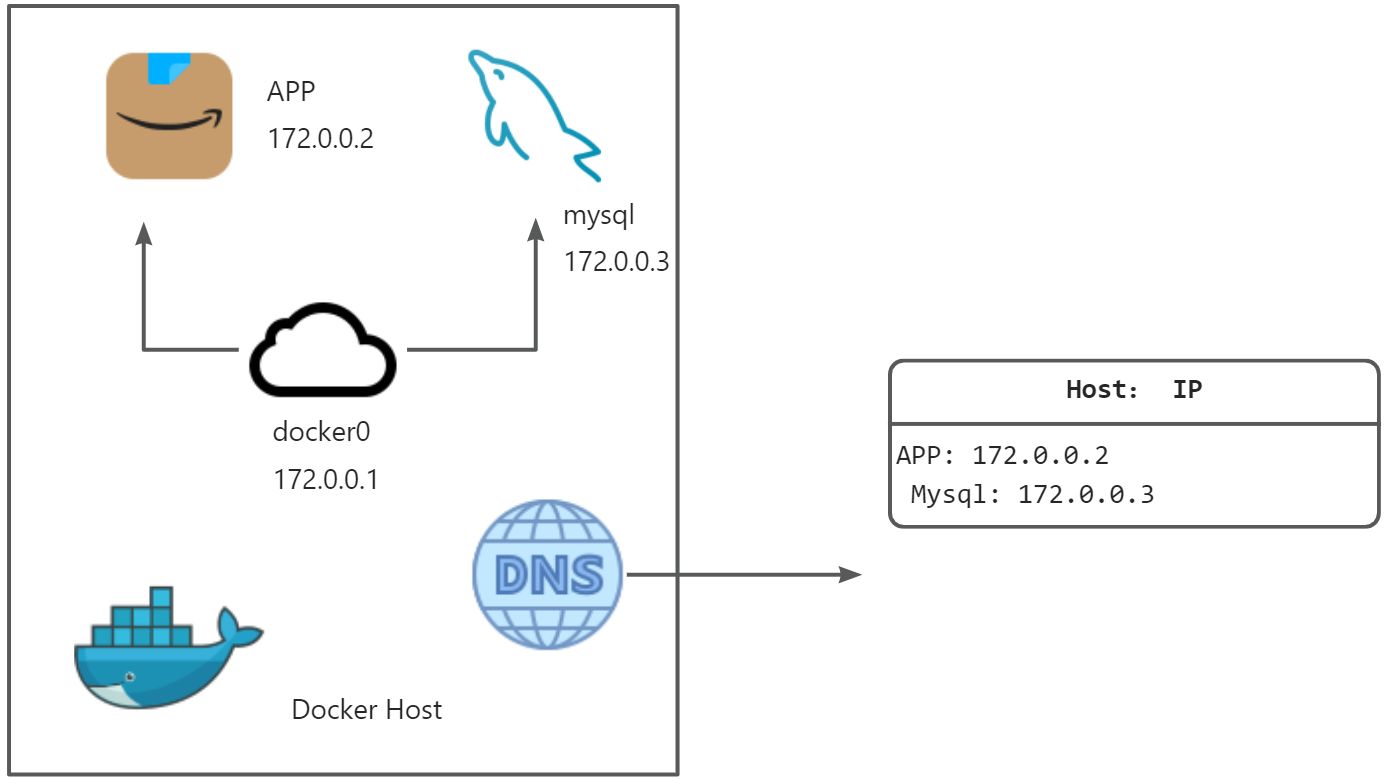
Docker随笔
OverView 为什么需要Docker 如果我需要部署一个服务,那么我需要提前部署其他应用栈,不同的应用栈会依赖于不用的操作系统和环境。这样做会产生一些负面影响: 不同版本依赖较长的部署时间不同的Dev/Test/Prod环境 这时我们需要一个工具去解…...
uni-app 前后端调用实例 基于Springboot
锋哥原创的uni-app视频教程: 2023版uniapp从入门到上天视频教程(Java后端无废话版),火爆更新中..._哔哩哔哩_bilibili2023版uniapp从入门到上天视频教程(Java后端无废话版),火爆更新中...共计23条视频,包括:第1讲 uni…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
